硅钢连退机组辐射管加热段数值模拟

王 骏 王 庆

(国网江苏综合能源服务有限公司)

脱碳退火是高牌号无取向硅钢生产过程中的关键工序之一，是为了完成初次再结晶，将基体中碳含量降到0.003%以下，有利于发展完善的二次再结晶组织，并去除硫和氮，消除产品的磁时效，同时，在钢带表面形成均匀且致密的SiO2薄膜[1]。目前国内高牌号无取向硅钢脱碳退火主要采用两段式退火方法，其机组主要组成是：预热无氧化炉(PH/NOF)、1号辐射管炉(1号RTF)、1号均热炉(1号SF)、2号辐射管炉(2号RTF)、2号均热炉(2号SF)、1号冷却段(1号CF)、2号冷却段(2号CF)，如图1所示。

图1 高牌号无取向硅钢脱碳退火机组炉段组成

带钢从PH/NOF入炉，从2号CF出炉，而保护气氛是从2号CF流向PH/NOF。一般情况下，1号RTF和1号SF通湿H2+N2混合气，使带钢脱碳；2号RTF和2号SF通干H2+N2混合气，使带钢在保护气氛中完成初次再结晶。

数值模拟技术已广泛应用于各行各业[2-7]，经过对多种数值方式的对比[8-13]，文章针对某公司硅钢厂连续退火机组的1号RTF，以段法为基础，建立该段炉内传热模型，并利用生产实际提供的数据对模型进行验证，为该公司连续退火机组节能控制提供理论依据。

1 物理模型

文章研究对象是某公司硅钢厂连续退火机组1号RTF炉段，主要用于带钢脱碳退火前的快速升温。其炉长22 m、炉内宽1.7 m、炉内高1.3 m、机组速度100 m/min、带钢尺寸1 200 mm×0.5 mm。炉子共设置自身预热U型辐射管烧嘴38套，实际生产中沿炉长分为2个控制段，每段19套辐射管烧嘴。为了降低燃料消耗量，寻求最佳燃料供给方式，并且不过多增加设备投资成本，模拟时将炉长方向分为3个控制段，第1、第3段各6对(12套)辐射管，第2段7对(14套)辐射管。

2 传热数学模型

建立的1号RTF数学模型包括：带钢表面能量平衡方程、炉壁表面段能量平衡方程、辐射管表面能量平衡方程及热电偶能量平衡方程。

2.1 基本假设

1号RTF采用辐射管加热，燃烧产生烟气在辐射管内，炉内充满氮氢保护气。机组内部压力前低后高，保护气从后向前流动，与炉内带钢、炉壁、辐射管进行对流换热。炉内辐射管、炉壁、带钢之间以辐射换热方式进行热交换。在连续稳定时，认为炉内传热过程为稳态过程，做如下假设：

(1)参与辐射换热的炉壁表面、带钢表面、辐射管表面均为灰表面；

(2)保护气体由氮气和氢气组成，露点在20 ℃左右，不参与辐射换热；

(3)忽略模型段间辐射；

(4)模型段内保护气温度均匀；

(5)带钢沿宽度方向上温度均匀；

(6)忽略炉内其他部件热损失。

2.2 模型段划分

将1号RTF沿炉长方向分为19个模型段，每段包含1对(2套)在带钢上下对称布置的辐射管烧嘴，如图2所示。模型段内参与辐射的表面分别称为带钢表面段、辐射管表面段和炉壁表面段。带钢运动方向与保护气体流动方向相反。

图2 1号RTF简化模型

2.3 带钢表面段能量平衡方程

带钢厚0.5 mm，根据模型假设，满足集总参数法[14]条件，即带钢厚度方向上温度均匀。燃料燃烧产生热量通过辐射管以辐射换热的方式向外传递。炉子稳定运行时，由于忽略了其他部件热损失，炉体耐材无蓄热，辐射管辐射出的热量将全部用于带钢升温，成为带钢蓄热量。因此，带钢表面段的能量平衡方程可以表示为：

Qs=Qr+Qcon

(1)

其中：

Qs=cs·ms·(Ts-Ts0)/τ

(2)

(3)

Qcon=h·(Tg-Ts)·Fs

(4)

炉气与带钢表面间的对流换热系数由Trinks公式[15]确定：

h=5.67+3.14ρω

(5)

式中:ρ为炉气密度，kg/m3；ω为炉气平均流速，m/s。

2.4 炉壁表面段能量平衡方程

模型段内，炉壁表面段与其他表面段之间以辐射换热方式进行热交换，与炉气之间进行对流换热。在稳态过程中，炉墙内外表面之间进行稳态导热，热流密度相等；其导热方程为：

(6)

边界条件：

Qw,in=Qw,out

(7)

(8)

(9)

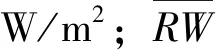
2.5 辐射管表面段能量平衡方程

燃气和助燃空气在辐射管内燃烧，燃烧产物在辐射管内流动并发生热交换。同样，在稳态条件下，假设：辐射管内气体流动状态稳定；忽略化学和机械不完全燃烧及热损失。这时，辐射管只是传递热量的中间载体，忽略辐射管导热热阻。那么，辐射管能量平衡方程的各分量式为：

(1)燃料燃烧的化学热Qcom,i=BiQd;

(2)燃料带入物理热Qfu,i=Bicfutfu;

(4)废气带走热Qf,i=Vicextad=BiVncextex。

根据文献[16]引入“孔模型”，得到辐射管排出废气温度与管内烟气温度的关系，即：

(10)

上述(1)～(4)构成了辐射管的能量平衡方程式：

Qcom,i+Qfu,i+Qr,i+Qf,i=0

(11)

经过整理，上式写成以Tr为未知量的一元四次方程：

(12)

可以求得辐射管的温度为：

(13)

式中：

将辐射管温度计算嵌套在炉壁的计算中，当炉壁达到稳态平衡的时候所计算出来的辐射管温度便是其真实值。

图3为RTF二维简化示意图，W代表炉墙；引入与辐射管相切的假想面[17]P1和P2，用于求解各表面间角系数；R为辐射管；S为带钢。将系统分为三个独立体系：W-P1、P1-R-P2、P2-S。通过分别求解三个独立体系中的角系数，最终得到系统的角系数。

图3 RTF二维简化模型

2.6 热电偶表面能量平衡方程

热电偶的测量温度实际上是炉内的“均衡温度”。热电偶热端与带钢、辐射管及炉壁进行辐射换热，与炉气之间进行对流换热。相对于其他表面，热电偶的表面积很小，对炉内各部分间的传热影响可忽略不计。

热电偶所测温度不仅与参与辐射表面段的分布有关，还与热电偶的位置、插入炉膛深度、气体流动状态、各表面黑度等诸多因素有关。在模型中，热电偶温度的计算基于各模型段，分散在各段中计算。

在热电偶的温度求解中，稳态时热电偶端的能量平衡方程为：

(14)

将上式整理成关于Tt的一元四次方程：

(15)

式中：

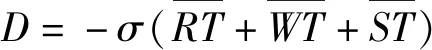
可求得热电偶温度为：

Tt=(-E/D)1/4

(16)

热电偶热端表面对炉内各表面段的角系数为：

式中：Y=D/b,Z=D/a,且D>R,D,R,a和b见图4。

图4 热电偶与其他表面间角系数计算模型

2.7 求解方法

材料的热物性参数采用线性插值法计算。各表面段以三元模型[18]法计算。在计算过程中，忽略段间辐射，实现了能量平衡方程组的解耦。采用MATLAB软件编写程序，带钢温度和炉壁内表面温度互为边界条件，迭代计算，计算流程如图5所示。

图5 计算流程

3 模型计算结果与讨论

3.1 模型验证

根据实际生产，对程序参数进行设定，以此验证模型的正确性。生产控制系统设定的带钢升温曲线、实际生产带钢升温曲线和模型计算带钢升温曲线的对比，如图6所示。其中计算所得带钢升温曲线比带钢实际温度略高，这是因为计算过程中，忽略了炉内其他部件热损失，而将这部分热损失都纳入带钢吸收热量，因此计算所得带钢温度偏高。然而，模型计算结果与实际生产带钢温度间最大温差不超过3%，可以认为该模型能够真实反映带钢在炉内的升温过程，可以用于该炉段内传热模拟计算。在炉段入口处，设定带钢温度比带钢实际温度略高，表明带钢进入该炉段时温度没有达到设定要求，可能是由于上一炉段(PH/NOF)能力不足所致。计算时，参数根据实际生产进行设置。

图6 带钢温度设定值、实际值、计算值对比

RTF炉内的传热方式主要为辐射传热和对流传热，带钢表面辐射传热热流密度和对流传热热流密度的对比，如图7所示。由图可以明显看出，辐射传热占主要地位，辐射传热热流密度大约是对流传热热流密度的36倍。同时，图7给出了炉内各表面段沿炉长方向的温度分布。

图7 各表面段温度及辐射热流密度与对流热流密度对比

3.2 燃料分配制度对带钢加热的影响

燃料分配制度决定了炉内的加热过程，也决定了带钢的加热效果。实际生产中，1号RTF被分成两个控制段，即38套辐射管烧嘴被分为两组，每组19套，炉子加热过程的灵活性不好。从炉子加热过程控制灵活性角度出发，分段越多越灵活。然而，在实际生产中，过多的分段会使操作更加复杂，同时会造成控制成本的急剧增加。因此，在考虑实际设备成本增加不多的情况下，将1号RTF分为3个控制段，第1段和第3段各6对(12套)辐射管烧嘴，第2段7对(14套)辐射管烧嘴。表1给出了3段控制模式下的燃料分配机制。燃料均匀分配机制中，各段燃料供给量相同，作为标准机制。对于1号和2号燃料分配机制，增加了第1段和第2段燃料供给量，减少第3段燃料供给。在满足带钢加热温度要求的前提下，1号和2号分配机制的燃料消耗量大于标准机制，也就是说，这两种方法没有达到节能目的。3号、4号和5号分配机制减少第1段的燃料供给量，而增加第3段的供给量，保持第2段燃料供给量不变。结果表明，在满足带钢加热要求的条件下，这3种方法总的燃料消耗量小于标准供给机制，第3段燃料供给量越多，总的燃料消耗量越少。

表1 燃料分配机制 %

不同燃料分配机制下带钢的温度曲线，如图8所示。1号和2号分配机制下，炉子中部带钢温度比其他机制要高，而带钢最终温度却较低。这是因为，这两种分配机制减少了炉子尾部供热量，导致炉尾带钢升温变慢。而对带钢的加热而言，更强调的是带钢最终温度，因此认为其余3种燃料分配机制更为合理。

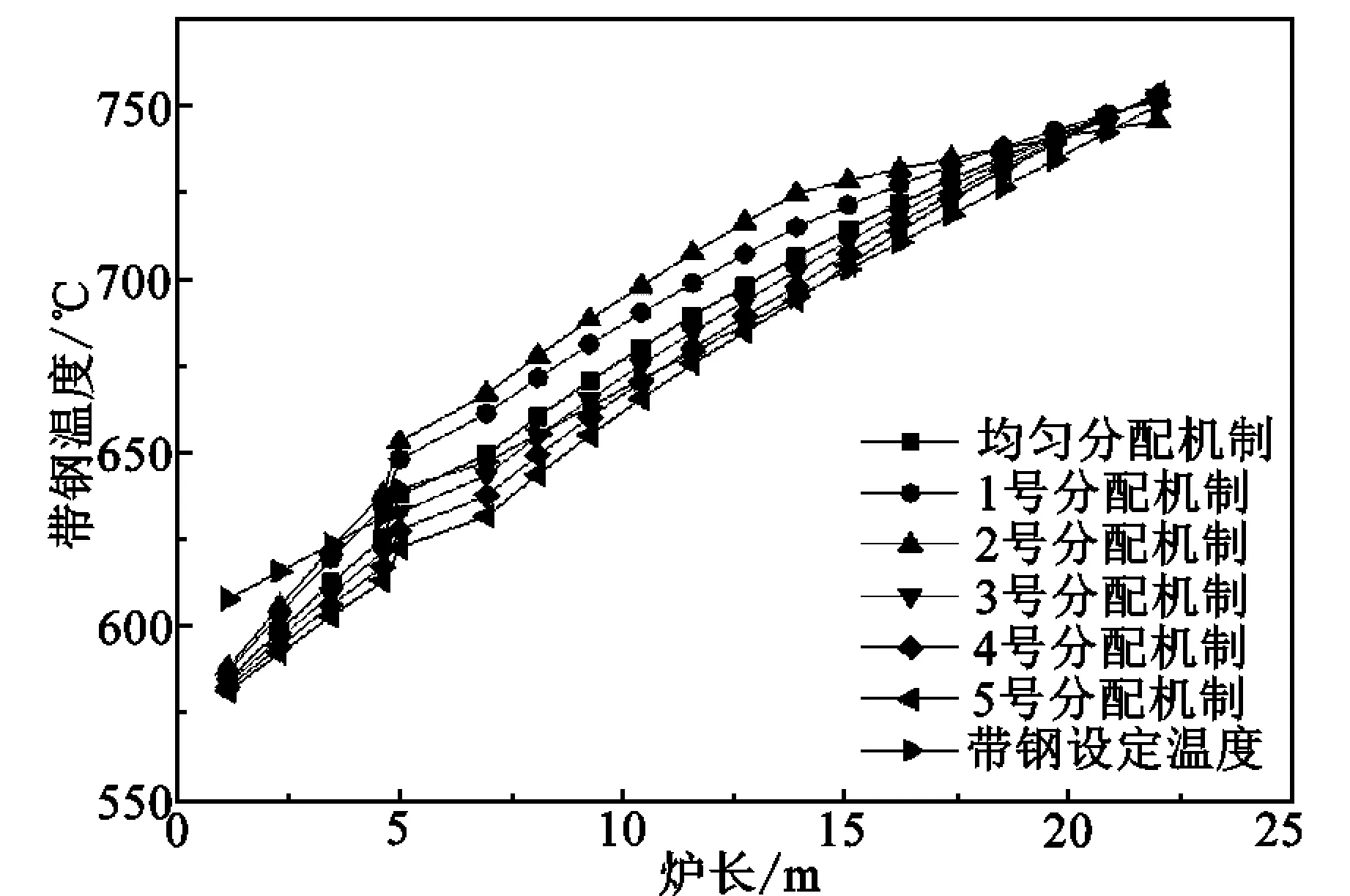
图8 不同燃料分配机制下带钢的温度

不同燃料分配机制下的带钢表面热流如图9所示。5号分配机制在带钢加热过程中热流保持比较均匀，也就是说，带钢加热过程中，5号分配机制在不同阶段都保持着带钢升温的较为恒定热流。对于1号和2号分配机制，整个RTF炉段中带钢表面热流均呈下降趋势，在第一控制段热流最大，第三控制段热流最小，这就解释了图8中该分配机制下第三控制段时带钢升温较慢的原因。随着第一控制段燃料分配量的减少，该段热流也减小，第三控制段的燃料分配量增加，热流量也增大，从而增强了该段的辐射温压。

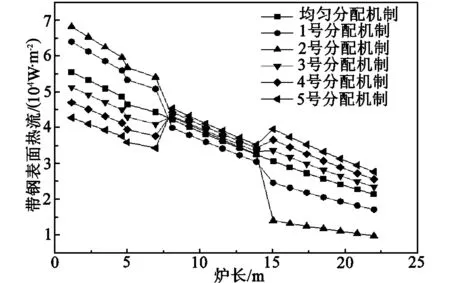
图9 不同燃料分配机制下的带钢表面热流

不同燃料分配机制下炉长方向辐射管表面温度的变化，如图10所示。5种分配机制中，第1控制段辐射管表面温度随着燃料供应量的减少而降低，第3控制段辐射管表面温度随着燃料供应量的增加而升高，使得各段辐射管间表面温差变大，这也是带钢加热过程需要的。想要带钢保持稳定的升温状态，必须保证带钢不同阶段的辐射温压，因此，沿炉长方向，辐射管表面温度应与带钢温度保证同样的上升趋势。结合图9和图10可以得出：5号燃料分配机制是最佳方案。

图10 不同燃料分配机制下炉长方向的辐射管表面温度

4 结论

基于段法理论，采用MATLAB软件编写程序，对国内某钢厂硅钢退火机组的1号RTF建立传热模型，开发出辐射管加热段的传热模型计算机数值仿真系统。采用实际生产参数对程序进行设定，并且进行了验证。计算结果表明，在1号RTF内，辐射传热量大约是对流传热量的36倍。对不同供热机制下的燃料消耗量、带钢表面热流密度以及辐射管温度进行了分析，综合对比，认为增强了第3控制段传热量的5号燃料分配机制为最优机制，在满足带钢加热要求的基础上最为节能。