基于非合作LEO卫星辅助GNSS联合定位技术

2022-02-18秦红磊姜穆元

导航定位与授时 2022年1期

秦红磊，姜穆元

(北京航空航天大学电子信息工程学院，北京 100083)

0 引言

全球卫星导航系统(Global Navigation Satellite System，GNSS)因具有全球性覆盖、全天候、高实时性和高精度的特点，在陆地、海洋等各类军事及民用领域得到了广泛的应用，已经成为目前最普遍的导航技术平台。尽管GNSS性能优越，但其缺点也逐渐暴露出来：

1)现代社会严重依赖于GNSS服务，然而传统的导航信号易受到欺骗，导致系统可靠性急剧下降；

2)GNSS卫星信号容易受到建筑物的遮挡，使得GNSS接收机在城市峡谷环境中经常出现由于可见卫星数目不足而无法完成定位的情况；

3)由于卫星信号到达地面功率很低，在强干扰情况下，会使导航信号无法被捕获与跟踪，造成定位失败。

随着位置服务需求范围的不断扩大，同时也为满足日益增长的军事应用需求,各国针对各自卫星导航系统进行了功能升级与信号体制的改进,但导航卫星信号到达地面功率低、易被干扰等缺陷仍未被完全解决。为降低对传统 GNSS的依赖，并提供一种新型辅助定位手段，考虑利用低轨(Low Earth Orbit，LEO)卫星在GNSS受挑战的环境中对其进行辅助。首先，LEO卫星与中地球轨道的GNSS卫星相比，其轨道高度相差近20倍，这使得LEO卫星信号到达地面的功率显著增强；其次，LEO卫星绕地球轨道运行的速度相比GNSS卫星要快得多，因此其多普勒测量将十分具有吸引力。除此之外，在未来几年，国内外将涌现出大量的低轨卫星系统，2015年，OneWeb公司宣布在未来构建一个含有648颗卫星的低轨卫星系统；同年，SpaceX和Google宣布合作构建一个含有更多卫星的低轨卫星系统，预计最终发射约4000颗卫星；三星公司和Boeing公司也分别启动了构建低轨卫星系统计划；国内也提出了如鸿雁全球卫星星座、虹云工程等计划。若以上星座最终构建成功，将会组成一个由数千颗LEO卫星为基础的庞大卫星宽带网络，使得它们在信号频率和轨道上丰富多样。

目前较为成熟的低轨卫星系统有铱星(Iridium NEXT)、ORBCOMM OG2和全球星(Globalstar)等。Globalstar卫星系统与ORBCOMM卫星系统本身均具备位置信息服务，铱星公司于2016年宣布在第二代卫星Iridium NEXT系统中增加定位服务，然而以上服务均需特许授权才可被使用，并且其具体技术细节不被公开。国内外基于LEO辅助GNSS的研究主要集中于两方面：一种是应用在精密单点定位(Precise Point Positioning, PPP)领域,利用LEO卫星运动速度快，在短时间内能够产生较大的空间几何变化，降低观测数据的时间相关性，从而提高整周模糊度浮点解的精度，缩短固定窄巷整周模糊度的时间；另一种是将LEO当作轨道降低的导航卫星与传统GNSS级联进行定位。但这两种应用都是以LEO卫星可播发伪距与载波相位信息为前提，而目前在轨LEO星座作为通信星座，不具备导航能力，即使像SpaceX等星座也是以提供宽带服务为主要业务，并不是为导航而设计的。

本文基于以上情况，提出了利用从LEO卫星信号中提取的多普勒与GNSS的伪距、多普勒进行联合定位，以解决在复杂环境下GNSS受到干扰导致可见星数目不足而无法定位的问题。

1 GNSS伪距定位算法

在颗全球定位系统(Global Positioning System，GPS)卫星可见的情况下，线性化后的伪距观测方程为

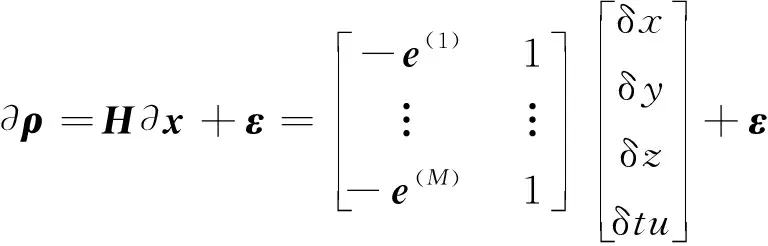
(1)

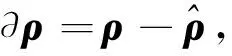
2 瞬时多普勒定位算法

式(1)两边同时对时间求微分得到

(2)

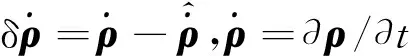
(3)

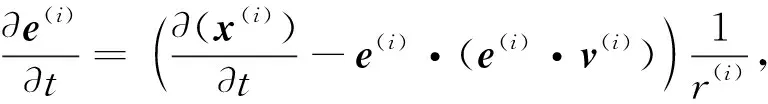
(4)

当同一时刻有4颗及以上卫星时，可以得到用户位置的瞬时解。

3 非合作LEO卫星辅助GNSS联合定位算法

卫星相对于地面做高速运动产生的多普勒频移能够反映卫星和用户终端之间的位置与速度关系，而从导航卫星处获得的伪距信息也反映着卫星与用户间的几何位置关系。因此，多普勒与伪距都将对用户位置起到约束作用。从几何角度分析，伪距方程表示一个以卫星位置为圆心、伪距为半径的球体，用户位于球体表面的一点。多普勒描绘了一个以卫星位置为顶点、卫星速度方向为轴线、用户与卫星间的视距方向为母线的圆锥，用户位于圆锥底部圆环上的一点。利用不同卫星的多普勒圆锥与伪距球体表面相交获得用户位置，即为伪距/多普勒联合定位原理的几何描述，如图1所示。

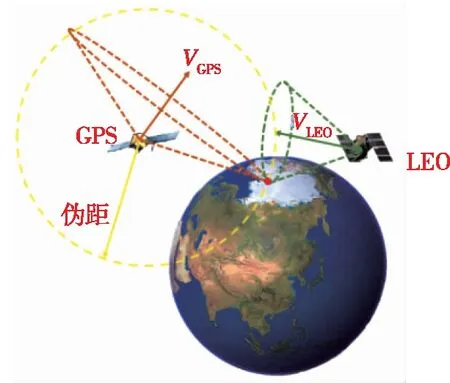
图1 伪距/多普勒的联合定位原理图Fig.1 Schematic diagram of pseudorange/Doppler joint positioning

(5)

4 仿真验证

在这一节中，通过仿真实验结果来验证本文提出模型的正确性与性能。目前，大部分文献采用的低轨卫星星座为铱星星座，该系统卫星数目较多，持续可见性好。而ORBCOMM卫星星座虽然卫星数目不及铱星星座，但相比于铱星的极地轨道，ORBCOMM采用的是倾斜轨道，使其具有更好的空间几何分布。在信号体制方面，铱星信号采用频分多址(Frequency-Division Multiple Access, FDMA)与时分多址(Time-Division Multiple Access, TDMA)调制方式，每隔4.32s播发一次信号，而ORBCOMM信号采用SDPSK(Symmetrical Differential Phase Shift Keying)调制方式，为连续信号，更能满足本文实时定位的需要。因此，本文以GPS星座联合ORBCOMM星座为例进行分析。

ORBCOMM公司于2008年宣布部署第二代卫星(OG2)星座，一共发射18颗OG2卫星，而目前共12颗OG2卫星在轨运行，均匀分布在4个主轨道平面。OG2卫星轨道高度为720 km，轨道倾角为47°，轨道周期为97min。其下行链路播发的频段区间为137MHz～138MHz，共分为13个信道，包含12个带宽为25 kHz的S1～S12信道，用于与用户终端通信;1个带宽为50 kHz的信道,用于与关口站通信，频带分配如图2所示。

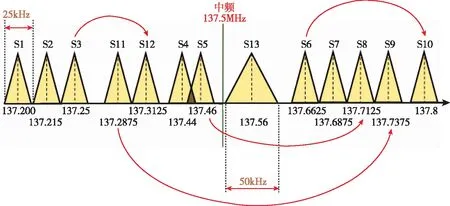
图2 ORBCOMM频带分配图Fig.2 ORBCOMM frequency band allocation diagram

用户下行链路采用SDPSK调制方式，数据率为4800bit/s，每颗ORBCOMM卫星播发各自在特定2个频带的信号。

使用STK11软件进行仿真，ORBCOMM轨道数据可采用北美防空司令部(North American Aerospace Defense Command, NORAD)的两行元素集(Two-Line Element，TLE)格式，由轨道参数和时间信息组成。采用SGP4预测模型进行重建。其中，ORBCOMM星座TLE卫星每天定期更新1～2次，可直接从NORAD网站celestrak.com获取。现假设用户位于北航篮球场，位置坐标为[-2.171623835652697×10;4.386021114668231×10;4.076293310911553×10]；仿真时间为北京时间2020年10月14日16:38:40.6，用户始终保持静止状态。此时卫星天空图如图3所示。

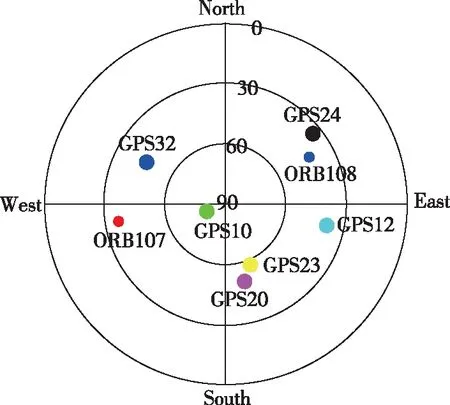
图3 仿真时刻卫星天空图Fig.3 Sky map of satellite at simulation time

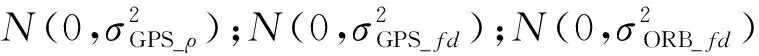
表1 各个卫星组合下的三维定位均方根误差

由于各类观测量的误差相互独立，且各自服从相同的高斯分布。因此，定位精度的差异将反映出卫星空间几何分布的好坏。通过分析比较可以看出，组合12+23; 12+20; 20+32; 23+32的精度较高，说明这几种组合空间几何分布最好。相反，组合12+24；20+23已明显偏离实际位置，此时雅克比矩阵在计算中出现奇异不能收敛，说明这几种组合的卫星空间分布较差。

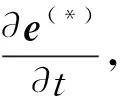
虽然百米甚至千米级的定位精度在传统GNSS领域是不够的，但若使用多GNSS系统级联则至少需要5颗及以上的卫星可见，这在遮挡严重区域或针对GNSS干扰区域是不易满足的。与之相比，ORBCOMM信号频率低，穿透性能好，频率与GNSS相差较大，信号功率远高于噪声，被干扰可能性较低。因此，当干扰地区GPS卫星数目不足无法定位时,即使是粗略的位置估计有时也是十分重要的。

从以上分析可以看出，2颗GPS+2颗ORB-COMM的组合是满足式(5)可求解的最低要求。在未来随着LEO的大量部署，可见的LEO卫星将逐渐增加。以定位精度较为一般的组合ORB107+ORB108+GPS10+GPS20为例，分析LEO数量的变化对定位精度的影响。由于ORBCOMM卫星目前只有12颗在轨运行，利用LEO卫星运动速度快、短时间内用户与卫星的空间几何变化较大的特点。以仿真时刻为中心，250s为步长，向左右各选取1个步长的ORB107,108作为第3,4,5,6颗LEO卫星，分别记为: ORB107′, ORB107″, ORB108′, ORB108″, 同样再通过MATLAB仿真软件在各理论观测值上叠加观测误差的经验值作为实测多普勒观测值，进行2000次蒙特卡罗仿真，定位结果如表2所示。