带电粒子在电磁场中运动问题归类分析

李金丑 宋丽飞

带电粒子在电磁场中的运动问题，不仅考查考生对共点力平衡、牛顿运动定律、抛体运动、圆周运动、功能关系等重要概念和规律的理解与应用，还考查考生通过受力分析、运动过程分析建构模型以及推理论证的能力。本文对此类习题进行了归类分析，主要归纳为以下四类问题。

一、带电粒子在磁场中的运动问题

1.经典习题

例1. 如图1，在平面直角坐标系Oxy的第一象限内，存在垂直纸面向外的匀强磁场，磁感应强度大小为B。大量质量为m、电量为q的相同粒子从y轴上的点，以相同的速率在纸面内沿不同方向先后射入磁场，设入射速度方向与y轴正方向的夹角为α（O≤α≤18O°）。当α= 15O°时，粒子垂直x轴离开磁场，不计粒子的重力。则（ ）

图1

A.粒子一定带正电

B.当α= 45°时，粒子也垂直x轴离开磁场

【简析】当α=150°时，粒子垂直x轴离开磁场，由左手定则可知粒子一定带正电，画出粒子运动轨迹图2，由图中几何关系可得，粒子轨迹半径为解得粒子入射速率为时，画出粒子轨迹如图3，可以直观地看出不能垂直x轴离开磁场；当在x轴上的射出点与P点的连线恰好等于轨迹的直径时，粒子离开磁场的位置到O点的距离最大（如图4），根据勾股定理解得最大距离为选项ACD正确。

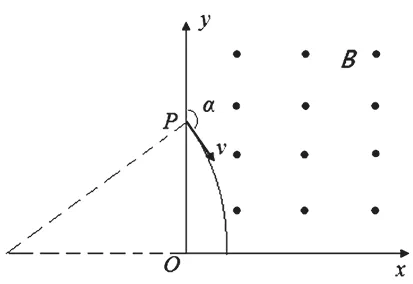
图2

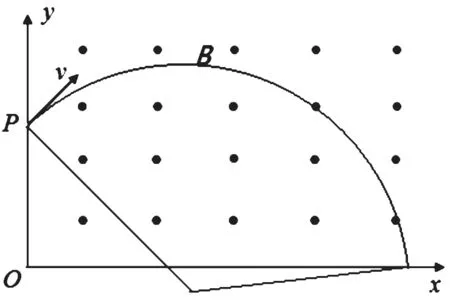
图3

图4

2.要点精析

（1）模型特点：带电粒子通常不计重力，在磁场中做匀速圆周运动。

（2）思路点拨：根据进入磁场和离开磁场的速度方向确定圆心的位置，利用好“垂直”“相切”“最远”等临界条件，画出粒子运动轨迹图帮助求解。

二、带电粒子在电场、磁场组合场中的运动问题

1.经典习题

例2.如图5，长度均为 的两块挡板竖直相对放置，间距也为，两挡板上边缘P和M处于同一水平线上，在该水平线的上方区域有方向竖直向下的匀强电场，电场强度大小为E；两挡板间有垂直纸面向外、磁感应强度大小可调节的匀强磁场。一质量为m，电荷量为q（q＞O）的粒子自电场中某处以大小为vO的速度水平向右发射，恰好从P点处射入磁场，从两挡板下边缘Q和N之间射出磁场，运动过程中粒子未与挡板碰撞。已知粒子射入磁场时的速度方向与PQ的夹角为6O°，不计重力。

图5

（1）求粒子发射位置到P点的距离；

（2）求磁感应强度大小的取值范围；

（3）若粒子正好从QN的中点射出磁场，求粒子在磁场中的轨迹与挡板MN的最近距离。

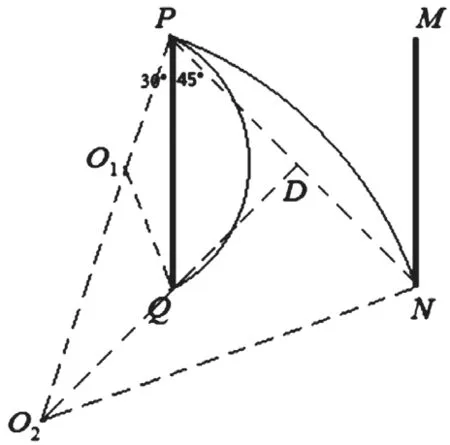
图6

图7

2.要点精析

（1）模型特点：带电粒子依次通过电场、磁场独立存在的场区，受力情况随区域不同而变化，不同区域适用不同的运动规律。电场力大多为恒力，带电粒子通常做匀变速直线运动或类平抛运动；磁场中通常做匀速圆周运动。

（2）思路点拨：速度是联系不同阶段运动的重要物理量，确定带电粒子在两个场区边界的速度（包括大小和方向）是解题的关键。根据受力分析和运动分析，大致画出粒子的运动轨迹，有利于问题的求解。结合题目情境，挖掘隐含条件，利用数学关系解决半径、最近或最远距离等问题。

三、带电粒子在电场、磁场叠加场中的运动问题

1.经典习题

例3. 霍尔元件是一种重要的磁传感器，可用在多种自动控制系统中。长方体半导体材料厚为a、宽为b、长为c，以长方体三边为坐标轴建立坐标系xyz，如图8所示。半导体中有电荷量均为e的自由电子与空穴两种载流子，空穴可看作带正电荷的自由移动粒子，单位体积内自由电子和空穴的数目分别为n和p。当半导体材料通有沿+x方向的恒定电流后，某时刻在半导体所在空间加一匀强磁场，磁感应强度的大小为B，沿+y方向，于是在z方向上很快建立稳定电场，称其为霍尔电场，已知电场强度大小为E，沿-z 方向。

图8

（1）判断刚加磁场瞬间自由电子受到的洛伦兹力方向；

（2）若自由电子定向移动在沿+x方向上形成的电流为In，求单个自由电子由于定向移动在z方向上受到洛伦兹力和霍尔电场力的合力大小Fnz；

（3）霍尔电场建立后，自由电子与空穴在z方向定向移动的速率分别为vnz、vpz，求△t时间内运动到半导体z方向的上表面的自由电子数与空穴数，并说明两种载流子在z方向上形成的电流应满足的条件。

【简析】（1）由左手定则可判断出自由电子受到的洛伦兹力沿+z方向；（2）设t时间内流过半导体垂直于x轴某一横截面自由电子的电荷量为q，由电流定义式有，设自由电子在x方向上定向移动速率为υnx，自由电子的电流微观表达式为In=neabυnx，单个自由电子所受洛伦兹力大小为F洛=eυnxB，霍尔电场力大小为F电=eE，自由电子在z方向上受到的洛伦兹力和霍尔电场力方向相同，其合力大小为设△t时间内在z方向上运动到半导体上表面的自由电子数为Nn、空穴数为Np，则Nn=nacυnz△t，Np=pacυpz△t，霍尔电场建立后，半导体z方向的上表面的电荷量就不再发生变化，应有Nn=Np，即在任何相等时间内运动到上表面的自由电子数与空穴数相等，这样两种载流子在z方向形成的电流大小相等、方向相反。

2.要点精析

（1）模型特点：带电粒子同时受到电场力与洛伦兹力，通常电场力为恒力，洛伦兹力有可能为恒力，也有可能为变力。

（2）思路点拨：若电场力和洛伦兹力平衡，则带电粒子做匀速直线运动；若电场力和洛伦兹力不平衡，则带电粒子将做复杂的曲线运动，因洛伦兹力不做功，通常应用动能定理求解。

四、带电粒子在交变场中的运动问题

判断离子在磁场中的运动情况是个难点，对考生空间立体想象能力要求较高，要求考生对运动独立性原理有深刻理解，在多维运动的情况下能应用这一重要物理观念分析求解问题。

1.经典习题

例4. 如图甲所示，空间站上某种离子推进器由离子源、间距为d的中间有小孔的两平行金属板M、N和边长为L的立方体构成，其后端面P为喷口。以金属板N的中心O为坐标原点，垂直立方体侧面和金属板建立x、y和z坐标轴。M、N板之间存在场强为E、方向沿z轴正方向的匀强电场；立方体内存在磁场，其磁感应强度沿z方向的分量始终为零，沿x和y方向的分量Bx和By随时间周期性变化规律如图乙所示，图中BO可调。氙离子（Xe2+）束从离子源小孔S射出，沿z方向匀速运动到M板，经电场加速进入磁场区域，最后从端面P射出，测得离子经电场加速后在金属板N中心点O处相对推进器的速度为υO。已知单个离子的质量为m、电荷量为2e，忽略离子间的相互作用，且射出的离子总质量远小于推进器的质量。

（1）求离子从小孔S射出时相对推进器的速度大小υs；

（2）不考虑在磁场突变时运动的离子，调节BO的值，使得从小孔S射出的离子均能从喷口后端面P射出，求BO的取值范围；

（3）设离子在磁场中的运动时间远小于磁场变化周期T，单位时间从端面P射出的离子数为n，且求图乙中tO时刻离子束对推进器作用力沿z轴方向的分力。

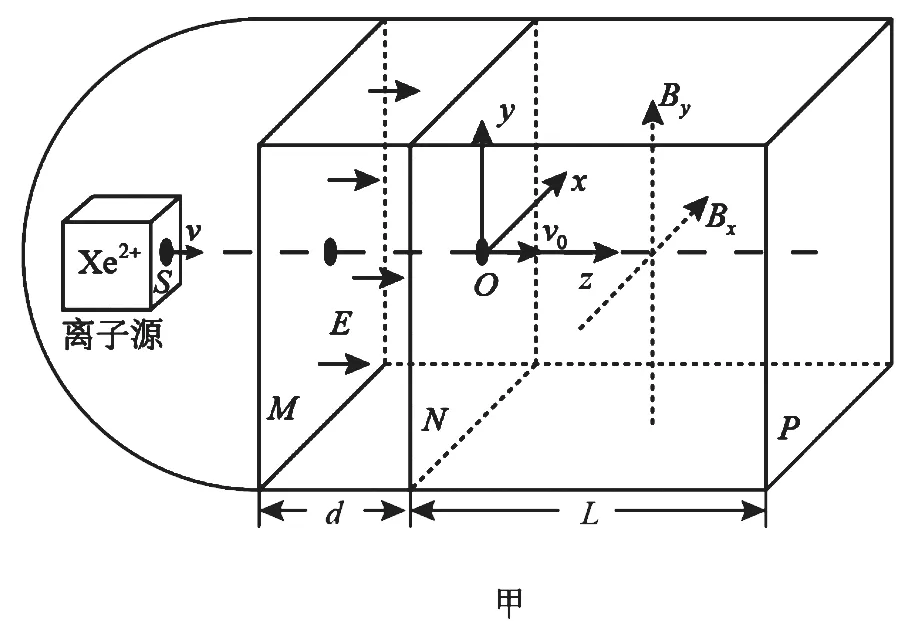
图9

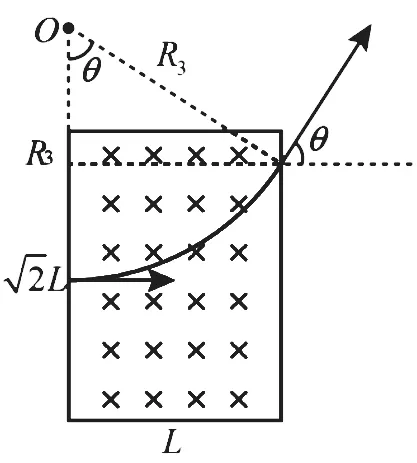
图10

2.要点精析

（1）模型特点：带电粒子依次经历交替变化的电场或磁场或叠加场，根据场区变换的情况以及粒子在场区运动的时间，可以分为两种类型：一种是电场或磁场在变化，但是同一带电粒子只经历一种确定的场区（如例4）；另一种是同一带电粒子会经历不同的场区，从而使运动分解成多个阶段，不同阶段适用不同的运动规律。

（2）思路点拨：首先，仔组分析电场、磁场的变化特点及相应的时间，确认粒子是按照上述哪类模型运动的；其次，粒子的运动情况不仅与交变电场和磁场的变化规律有关，还与粒子进入场区的时刻有关；最后，如果是同一粒子沿途经历不同的场区，要关注场区变换时粒子的位置与速度（包括大小和方向），尽量准确画出粒子运动的轨迹来构造几何图形，综合运用物理规律和几何关系来分析解决问题。