分段解决掌握好 切线放缩显灵妙——一道含绝对值函数题的解析

杨 飞

一、试题评价

例题：函数的最小值

二、一题多解

思路1：把含绝对值的函数写成分段函数，逐段求最小值，再通过比较得到最小值。

解法1：由题意

所以函数f（x）的最小值为1.

思路2：根据绝对值的定义对进行“放缩”，将其转化为函数y=2x-1-2lnx，再利用导数求最小值。

解法2：因为令g（′x）=0，解得x=1，易知x=1是函数g（x）极值点，所以函数g（x）min=g（1）=1，而当x=1时所以f（x）≥g（x）≥g（1）=1，所以f（x）min=1.

思路3：根据绝对值的定义对进行“放缩”，再根据lnx≤x-1进行“切线放缩”。

解法3：因为

思路4：先根据lnx≤x-1进行“切线放缩”，再利用“绝对值不等式”性质求得最值。

解法4：因为lnx≤x-1，则

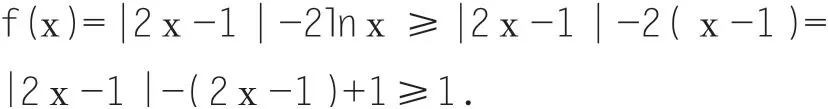
当且仅当x=1时等号成立，所以f（x）的最小值为1.

思路5：数形结合。

解法5：令和h（x）=2lnx，则f（x）的最小值为这两个函数图象上横坐标相同的点的距离的最小值，易求得h（x）在（1，0）处的切线方程为y=2x-2. 如图：

则x=1时距离最小为g（1）-h（1）=1，所以f（x）的最小值为1.

三、解法反思

1.解含绝对值函数试题的基本途径是去掉绝对值，常见的策略有以下两种：

（1）等价转化策略：①根据绝对值定义，讨论绝对值符号内式子的正负，将其写成分段函数；②根据绝对值的几何意义，即绝对值表示“变量”和定点之间的距离，如：表示数轴上的动点到定点-1和2的距离之和；③通过“平方”把绝对值运算转化为平方运算。

2.对于“超越”函数的最值问题，导数的工具性不容忽视。

3.把握式子的结构特征，运用常见的“切线放缩”。

4.运用数形结合思想，将函数的最值转化为两个函数图象上横坐标相同的两点间的距离。