基于深度强化学习的四旋翼无人机航线跟随

杨志鹏 李 波 甘志刚 梁诗阳

1.西北工业大学电子信息学院 陕西 西安 710072 2.湖北航天技术研究院总体设计所 湖北 武汉 430040 3.中国电子科技集团公司数据链技术重点实验室 陕西 西安 710077 4.中航工业洛阳电光设备研究所 河南 洛阳 471000

无人机在军事预警、工业巡检、抢险救灾、生活辅助等诸多领域所扮演的角色愈演愈烈, 人们对其智能化要求也越来越高[1-3]. 由于诸多原因, 无人机自主决策与控制在智能控制领域仍然面临巨大的挑战[4].一方面, 无人机空气动力学建模十分困难；另一方面,受诸多因素影响, 无人机在高空飞行时, 无法对外部或内部不确定因素的改变作出合理反应, 这大大提高了旋翼无人机在军事应用领域的难度[5]. 因此, 为了使旋翼无人机的行为适应未知的条件, 为无人机培养学习能力是至关重要的[6].学习和适应行为的最常见框架之一就是强化学习（reinforcement learning）——在与环境交互的过程中, 智能体利用自身行为的经验, 和对行为奖惩的反馈, 通过不断尝试, 从错误中学习, 最后找到规律, 作出合理的行为[7]. 因此, 强化学习方法已成为改善无人机自主行为的一种很有前途的工具[8].

为了使无人机能够实现完全自主的飞行并作出智能决策以完成任务, 有必要构建一个合理有效的无人机控制模型[9]. 强化学习可以有效地应用于高层决策系统, 从而使无人机提前掌握航线跟随的本领,防止人为操纵使其受不可控因素影响. 本文的主要目的是, 将神经网络（neural networks, NNs）与强化学习算法结合所形成的深度强化学习算法, 作为无人机在不确定环境下的高层控制[10], 使无人机学习自主决策, 完成航线跟随任务[11].

本文所进行的无人机航线跟随实验代表了四旋翼无人机在军事领域中的潜在应用之一[12]. 通过提出一种基于深度强化学习的新方法, 采用离线学习对神经网络进行训练, 将训练时产生的经验存储于经验池中,为神经网络的优化提供训练样本[13]. 并结合四旋翼无人机飞行特性和姿态控制要求, 设计环境空间、状态空间、动作空间和奖惩机制, 以提高深度强化学习模型的泛化能力[14]. 最后, 结合仿真结果, 验证了该方法对四旋翼无人机航线跟随的有效控制.

1 四旋翼无人机模型

本文重点关注四旋翼无人机动力学模型本身的系统性和规范性, 而不考虑风向、风速、电机损耗等外界或不可控因素的影响. 针对四旋翼无人机工作原理及其动力学模型构建过程, 作出详细的解释.

1.1 四旋翼无人机工作原理

四旋翼无人机通过调节4 个电机转速来改变旋翼转速, 从而改变无人机所受升力大小, 实现对无人机的运动控制和姿态控制, 进而, 旋翼旋转得越快,升力就越大, 反之亦然. 当4 个旋翼转动所提供的升力之和等于无人机自身重力时, 无人机就会保持悬停状态. 在悬停状态下, 4 个电机转速同时增大或减小, 无人机垂直上升或下降. 保持M1和M3电机转速不变, 当增加（减小）M2转速或减小（增加）M4转速时,无人机滚动运动（侧向运动）. 保持M2和M4电机转速不变, 当增加（减小）M1转速或减小（增加）M3转速,无人机俯仰（前后运动）. 当M1、M3电机转速同时增加（减小）或M2、M4的电机转速同时减小（增加）,无人机会旋转, 实现偏航[15].

通过组合以上的基本运动, 可以实现小型四旋翼无人机的各种复杂运动. 四旋翼飞行器的结构俯视图如图1 所示.

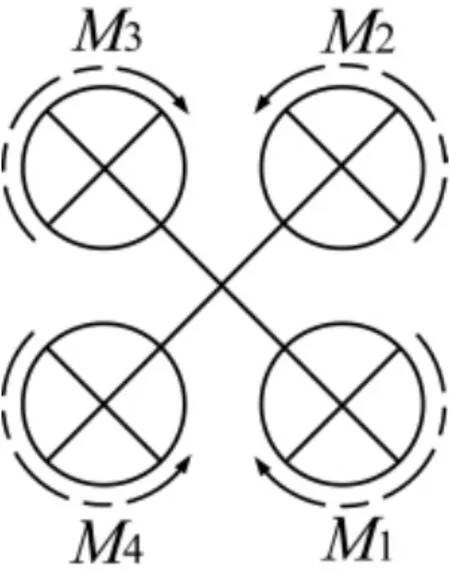
图1 四旋翼无人机俯视图Fig.1 The vertical view of quadrotor UAV

1.2 四旋翼无人机动力学模型

四旋翼无人机的坐标（x, y, z）是由其质心相对于惯性坐标系的位置决定的, 其姿态由欧拉角（滚动角, 俯仰角θ 和偏航角）来描述. 因此, 可以使用上述欧拉角来定义从机体坐标系Cb到惯性坐标系Ci的转换矩阵R：

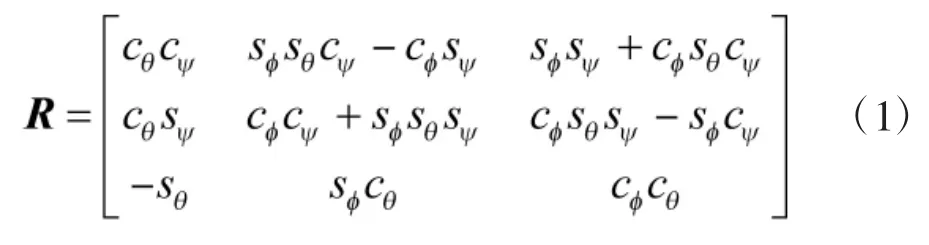
其中, s*表示角的正弦值, c*表示角的余弦值. 通过在机体坐标系和惯性坐标系之间使用这种转换, 可以从其他的力中分离出重力, 在惯性坐标系Ci中的转换动力学模型如下：

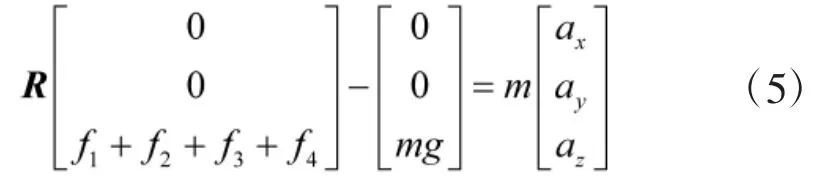
结合旋转矩阵R, 可得出:

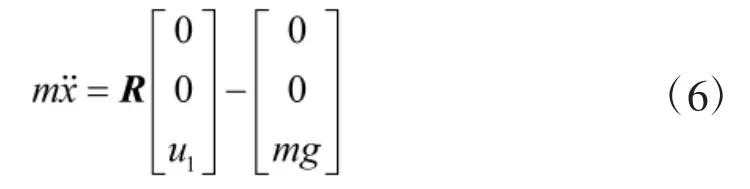
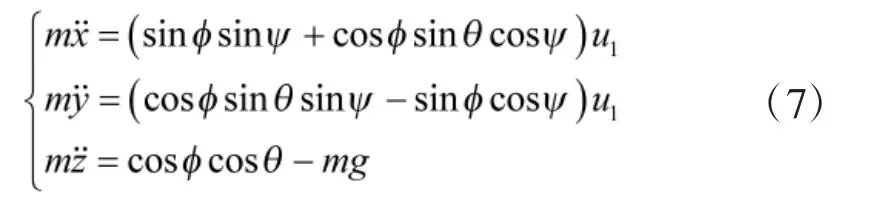
在惯性坐标系Ci中,令r=[x,y,z]T,其中,x、y、z分别表示四旋翼无人机在惯性坐标系中的位置. 令转动惯量矩阵J=diag（Jxx, Jyy, Jzz）,对于本文所选用的“+”型结构的四旋翼无人机来说, 高度通道的受力为：

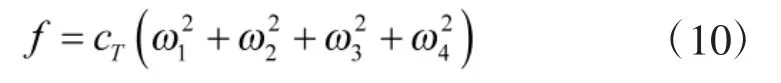
结合模型, 可以用3 个扭矩和总推力来描述四旋翼无人机的飞行输入μ：

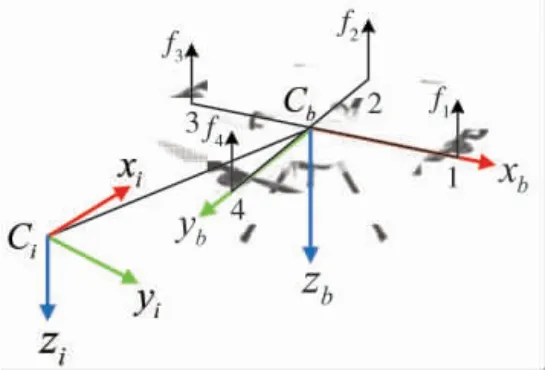
图2 四旋翼无人机模型与坐标系Fig.2 Model and coordinate system of quadrotor UAV

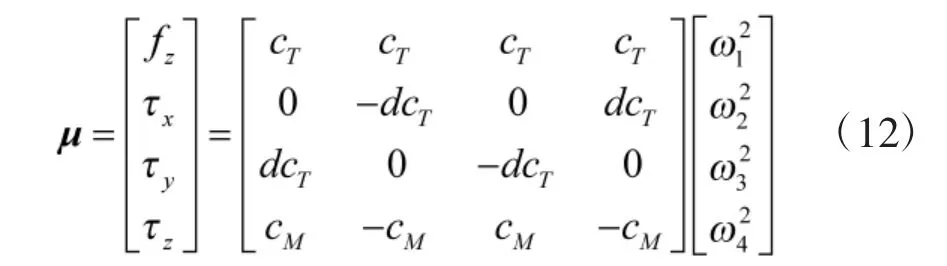
其中, d 表示每个电机到无人机中心的距离；cT表示推力系数；cM表示力矩系数. 在虚拟环境中, 四旋翼无人机的状态输入包括无人机的位置量、欧拉角、线速度和角速度, 其状态输入可表示为：

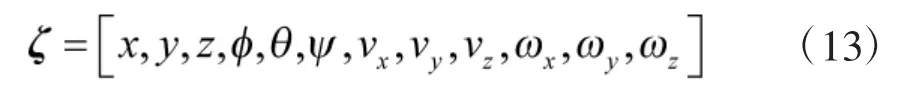
本文训练所设定的四旋翼飞机质量m=0.65 kg,力臂长度d=0.23 m, 推力系数cT=0.000 03, 力矩系数cM=0.000 9, 每个电机提供最大推力为3.19 N, 参数[Jxx, Jyy, Jzz]=[0.007 5, 0.007 5, 0.013].

2 深度强化学习算法

本文所建立的四旋翼无人机航线跟随模型, 采用的是基于深度强化学习的（deep deterministic policy gradient, DDPG）算法, 包括强化学习理论和基于神经网络运用的深度强化学习算法. 对于DDPG 算法而言,如何导入四旋翼无人机运动学、动力学模型和如何优化算法使之更易收敛是本文要解决的两个重要问题.

2.1 强化学习

强化学习是一种机器学习方法. 当环境中的智能体需要完成某种决策或任务时, 首要的步骤是采取相应的动作（action）与环境进行交互沟通, 在该动作变量的作用下, 智能体会产生新的状态量（state）,并在环境的反馈下, 得到一个相应的回报值（reward）.随着智能体不断试错, 强化学习算法利用产生的数据来完善并更新自身的策略. 通过不断地与环境交互, 智能体会逐渐学习到能够获取高额回报的动作值, 并不断改善自身的行为以适应不断变化的环境,最终学习到完成相应任务的最优策略.

图3 展示了强化学习实现的基本过程, 该过程可以用马尔可夫决策过程表示. 马尔科夫决策过程由元组表示, 其中,为智能体的状态量集合；为智能体的动作量集合；表示智能体在状态量为s, 且采取动作量为a 的条件下, 能够到达状态量s'的概率；R 为设定的奖励函数, 是智能体学习的“动力”和“方向”；γ 为折扣系数, 用于计算整个过程中的回报累计值. 折扣系数越大, 表示越注重长期收益. 根据已知量, 可推导出智能体的累计回报值为：

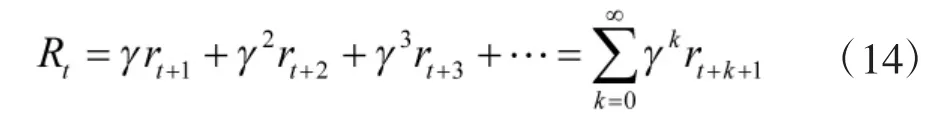
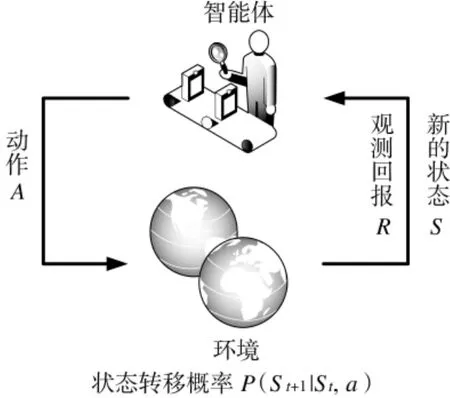
图3 强化学习理论基本框架Fig.3 Basic framework of reinforcement learning theory

强化学习的目的是学习到完成任务的最佳策略,使得累计回报最高, 即：

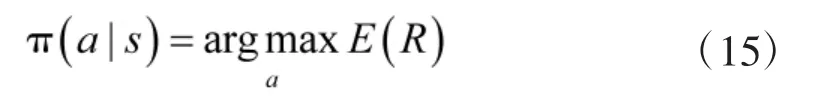
累计回报在状态s 处的期望值定义为状态-值函数：

与之对应的, 状态-行为值函数为：

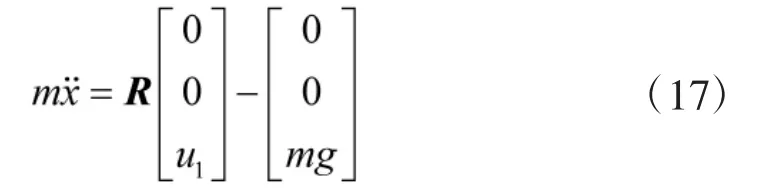
从强化学习的基本原理可以得出, 强化学习的学习行为是一个不断交互、不断变化的过程. 其中采取的动作、得到的奖惩和收集到的数据, 也是随着与环境不断交互得到的, 因此, 整个学习过程较其他机器学习算法更为智能化. 由于传统的强化学习算法如Q-learning 算法、Sarsa 算法等只能用于解决简单的离散化动作的环境, 无法解决四旋翼无人机飞行产生的连续性动作改变. 故本文选取的算法为基于深度强化学习的DDPG 算法.

2.2 基于深度强化学习的DDPG 算法

图4 为基于深度强化学习DDPG 算法的四旋翼无人机航线跟随策略学习过程示意图. 该算法通过actor 动作网络产生飞行策略, 并加入随机探索因子保证无人机有一定几率学习到未知动作, 通过无人机模型对数据处理, 得到无人机的状态信息, 并通过设计好的奖励函数, 得到无人机从状态st作出动作a到达下一状态st+1所获得的奖励值rt, 并将“状态, 动作, 奖励, 下一状态”存入经验池, 每过一段回合随机从经验池中抽取一定数目的数据, 采用梯度下降的方法对动作网络和评估网络进行训练, 并用主网络参数替代目标网络参数. DDPG 算法的核心是深度Q网络（deep Q network, DQN）算法和演员评论家（actor critic, AC）算法.

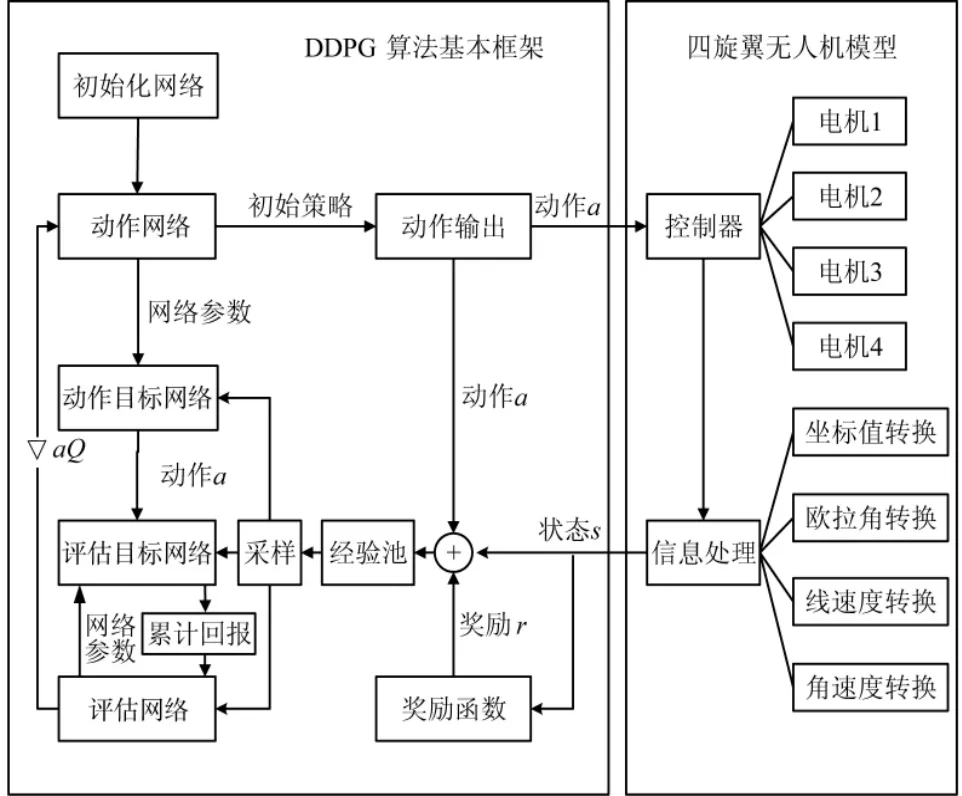
图4 基于DDPG 算法的策略学习过程示意图Fig.4 Diagram of strategy learning process based on DDPG

DQN 算法是在传统Q-learning 算法的基础加入神经网络, 有效避免了Q 表格存储爆炸的问题. 再通过添加target 目标网络, 并定期将主网络的参数更新至目标网络中, 有效打乱了数据的相关性.

AC 算法是基于策略的算法, 通过建立动作网络（action, A）和评估网络（critic, C）, 其中, A 网络负责识别智能体与环境交互的信息并产生的策略动作a,C 网络通过学习环境和获得奖惩之间的关系, 以评判A 网络产生的动作a 好坏. 较传统Policy Gradient算法, 该算法能够实现单步更新, 使训练更为高效.

本实验中,设定神经网络的输入s 为无人机各项状态量ζ,神经网络的输出a 为无人机4 个电机转速量.为方便神经网络的计算,对神经网络输入的状态空间O 和神经网络输出的动作空间M 作归一化处理,即：

其中, ωmax表示无人机电机最大转速. 归一化处理后的状态空间内和动作空间内各变量满足sn∈[1, -1]、an∈[0, 1]. 再综合考虑无人机飞行距离、飞行姿态、飞行线速度、飞行角速度等因素权重, 对无人机智能体进行相应的奖惩. 本实验中, 设定奖励函数为：

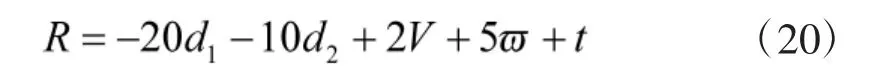
其中, d1表示无人机到航线终点的距离, d2表示无人机到航线的偏差距离, V、分别表示无人机飞行的合线速度值、合角速度值, t 为实验中无人机智能体保持安全飞行的时间. 在经验池收集满后, 每次抽取一定量的数据, 对神经网络参数进行更新. 再将学习效率进行周期性指数衰减, 使学习更易收敛.

3 仿真实验与结果分析

3.1 仿真环境

为了验证DDPG 算法对四旋翼无人机航线跟随策略学习的真实、有效性, 本次实验在GPU 服务器、Tensorflow 1.8.0、OpenAIGym、Python3.6 的环境（如图5 所示）对四旋翼无人机进行训练. 通过将四旋翼无人机动力学模型整合到建立的gym-aero 环境中,再导入DDPG 算法对无人机进行训练.

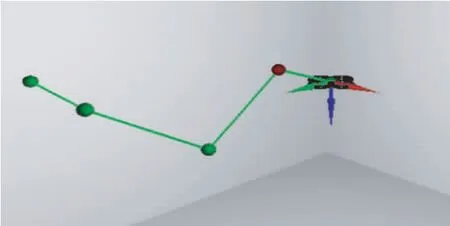
图5 基于gym-aero 的四旋翼无人机飞行仿真环境Fig.5 Simulation environment of quadrotor UAV based on gym-aero

本实验构建的A 网络、C 网络及其目标网络为BP 神经网络, 其中, 输入层一层、隐藏层一层、输出层一层, 设定隐藏层中神经元个数为150. 实验中, 设定无人机每个电机的最大转速为319.15 rad/s, 无人机悬停转速为225.67 rad/s. 在DDPG 算法的应用中,设立var 表示探索变量. 当每次和环境交互时, A 网络会生成动作值a, 系统再从以a 为均值、var 为方差的正态分布中随机取出新的值, 有利于无人机学习未知动作. 设定探索变量初始值为3, 随着四旋翼无人机不断地训练学习, var 值进行指数衰减. 设定A 网络和C 网络学习速率分别为0.001 和0.002, 奖励折扣系数为0.97. 当设定的经验池存满数据后,神经网络中采用自适应矩估计（adaptive moment estimation, Adam）的梯度下降优化方法更新参数, 每次从经验池抽取的经验数量为32.

3.2 实验结果

为实现安全的自主飞行, 四旋翼无人机应该时刻监视当前的时间状态, 以保证在有限资源、有限时间内, 完成相应的航线跟随任务. 因此, 在仿真环境中, 将时间状态t 加入到无人机的状态输入量ζ 之中.设定T=15 s 为虚拟环境中无人机满电量时的飞行续航时间, 当无人机在设定时间T 内未完成飞行任务时, 无人机能源耗尽, 航线跟随任务失败.

所有的实验中, 设立固定的四轴飞行器的初始位置和随机的目标航线. 在仿真实验中, 四旋翼无人机需要连续飞行到4 个连续的航路点, 且每个航路点从一个球体的体积均匀采样. 实验中, 用绿线表示飞行时无人机需要跟随的航线, 用红线表示四轴无人机的真实航迹.

按照上述环境和参数值, 根据2.2 节给出的基于深度强化学习的DDPG 算法步骤从初始状态开始运行, 当完成航线跟随任务或飞行续航时间内未完成航线跟随任务时, 回合终止, 进入下一回合学习. 在训练前期, 环境中的智能体进行地图探索, 并学习策略以使获得的奖励达到更大. 图6 为四旋翼无人机训练4 000 回合后的航线跟随任务展示. 在时间T4000=8.55 s 时, 无人机成功完成航线跟随任务. 可以看到, 在第2 段路径中, 无人机飞行轨迹与预设航线有较大的偏差, 这表明本文算法对无人机的训练是有效的, 但还无法保证无人机的持续稳定飞行.

图6 训练4 000 回合后的航线跟随任务展示图Fig.6 Exploded view of track following mission after 4 000 rounds of training

随着神经网络的训练进行, 算法的收敛程度不断提高. 如图7 所示, 当训练7 000 回合后, 四旋翼无人机已基本能够按照任务航线完成飞行. 此时T7000=11.65 s>T4000, 表示无人机在训练过程中提升了精度但降低了飞行效率, 未达到理想效果.

图7 训练7 000 回合后的航线跟随任务展示图Fig.7 Exploded view of track following mission after 7 000 rounds of training

此外, 由于任务中航路的不断变化, 四旋翼无人机对不同的环境作出反应需要一定的时间, 所以需要对无人机进行持续训练. 在算法中, 设定A 网络和C 网络学习速率每千回合衰减一半, 防止由于学习速率持续过大造成神经网络过拟合而产生低效学习、无效学习等问题.

经过足够的训练后, 无人机能够跟随任意随机航线进行飞行, 这表明训练出的神经网络能够对随机航线作出应对, 泛化能力较强. 图8 为四旋翼无人机训练10 000 回合后的航线跟随任务展示图. 可以清楚地看到, 在时间T10000=6.70 s 时, 无人机已经能够高精度完成任务航线的跟随, 此时训练效果较为理想.

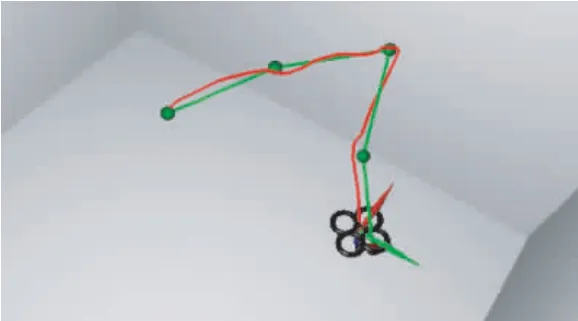
图8 训练10 000 回合后的航线跟随任务展示图Fig.8 Exploded view of track following mission after 10 000 rounds of training

随着训练回合的递增, 无人机受到的平均奖励逐渐递增, 最终趋于稳定. 图9 为四旋翼无人机的训练效果图, 其中, 横坐标表示训练回合数, 纵坐标表示每回合内无人机得到的平均奖励. 该训练效果图清晰展示了基于深度强化学习的DDPG 算法对四旋翼无人机航线跟随任务学习的促进作用.

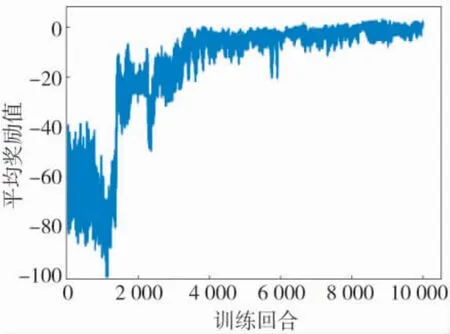
图9 四旋翼无人机训练效果图Fig.9 The training renderings of quadrotor UAV

4 结论

本文基于深度强化学习算法, 导入四旋翼飞行器非线性飞行运动学和动力学模型, 并建立了无人机航线跟随决策规则的产生方法, 避免了在不确定性环境中人为操作无人机飞行的繁琐性和粗疏性,使得无人机完成航线跟随任务更为有效. 动态学习的过程和训练方法使无人机智能决策和控制更为高效和精准, 从而能够使四旋翼无人机在接近真实的环境中学习到航线跟随等相关任务, 有利于实现无人机自主飞行与决策.