遥控武器站独立观瞄器零位校正方法研究
2022-02-17安玉陈健龙马俊波孙克文侯文
安玉,陈健龙,马俊波,孙克文,侯文
(1.中北大学 信息与通信工程学院,山西太原,030051;2.中国长峰机电技术研究设计院,北京,100854;3.中国人民解放军31619部队教研部,江苏南京,212400)
0 引言
随着现代科技的迅速发展,世界各国对军事控制权的争夺愈演愈烈,对武器装备的性能要求不断提高,遥控武器站就是世界主要军事强国对兼具高机动性能、快速反应能力和防护能力的武器系统迫切需求着重发展的新型武器装备,其是适应局部冲突,反恐防爆等新形势战争的高科技、智能化武器装备,具备高通用性、高精度、高智能化等一系列显著特性,可通过车内人员遥控实现对目标的快速搜索与精准打击,提升武器作战性能的同时能更好的保障操作士兵的安全。遥控武器站主要结构包括:上架部件、下架部件、缓冲摇架、光瞄以及相应的驱动单元[1-2]。
为了使枪械保持良好的作战状态,进行作战之前都要进行枪械校正,遥控武器站也是如此,在进行作战之前,也要进行枪械的校正,但是一般在进行枪械校正之前,遥控武器站光电观瞄系统的零位可能会发生漂移,因此在进行枪械校正之前要先进行光电观瞄器的零位校正(这也可以看作是枪械校正的一部分)。
针对此本文提出一种简洁的校正算法—坐标转换法,此方法是一种更简单有效的校正方法,也为以后的枪械校正提供了参考。
1 空间坐标转换
两个不同的直角坐标系之间的关系,总能够看成一个直角坐标系由另一个直角坐标系平移一次和旋转3次得到[3]。
1.1 平移转换
在此我们先来讨论两坐标系之间的平移,直角坐标系如图1所示,O1-X1Y1Z1为固定坐标系,i1、j1、k1为此坐标系下的正交单位向量,空间中有另外一个坐标系O2-X2Y2Z2,其三个坐标轴分别与O1-X1Y1Z1坐标系的三个坐标轴平行且方向相同,i2、j2、k2为此坐标系下的正交单位向量。

图1 O1—X1Y1Z1坐标系平移得到O2—X2Y2Z2
这里就不妨认为O2坐标系由O1坐标系平移得到,可以写出:,其中,a、b、c是O2坐标系的原点在O1坐标系中的坐标值,并且两坐标系的基矢量i1、j1、k1与 i2、j2、k2的关系为:

1.2 旋转转换
一个刚体绕一固定点有三个自由度,同样一个直角坐标系绕其原点的旋转也能由三个独立的旋转角来表示,文中用“方向角”、“俯仰角”、“滚转角”体系来表示。方向角将O2-X2Y2Z2坐标系以O2-X2Y2平面旋转α角度得到坐标系O2-X3Y3Z3,(在建立坐标系时,一定要注意右手原则和角度的正向,比如在O2-X2Y2面旋转的方向为X2→X3旋转的方向)如图2所示。
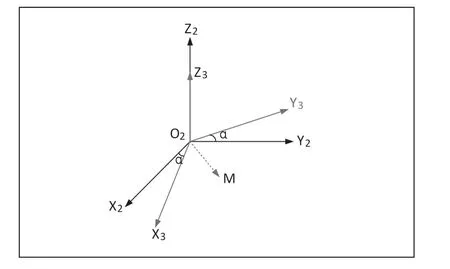
图2 O2—X2Y2Z2坐标系以O2—X2Y2平面旋转α得到O2—X3Y3Z3
i3、j3、k3为此坐标系下的正交单位向量。两坐标系的基矢量i3、j3、k3与 i2、j2、k2的关系为:
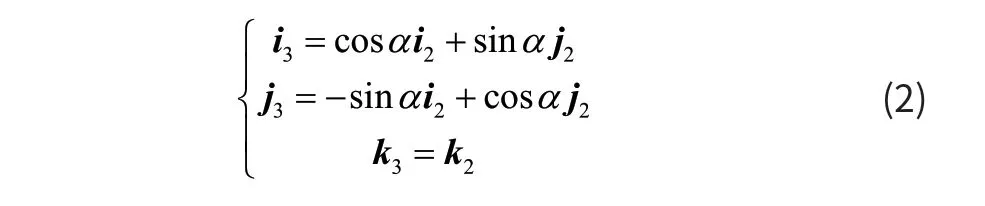
即:

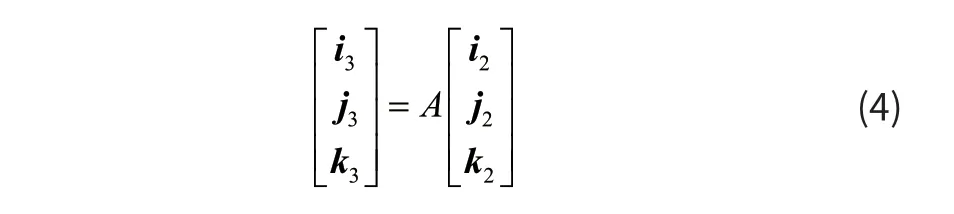
将O2-X3Y3Z3坐标系以O2-Y3Z3平面旋转β角度得到坐标系O2-X4Y4Z4,如图3所示。
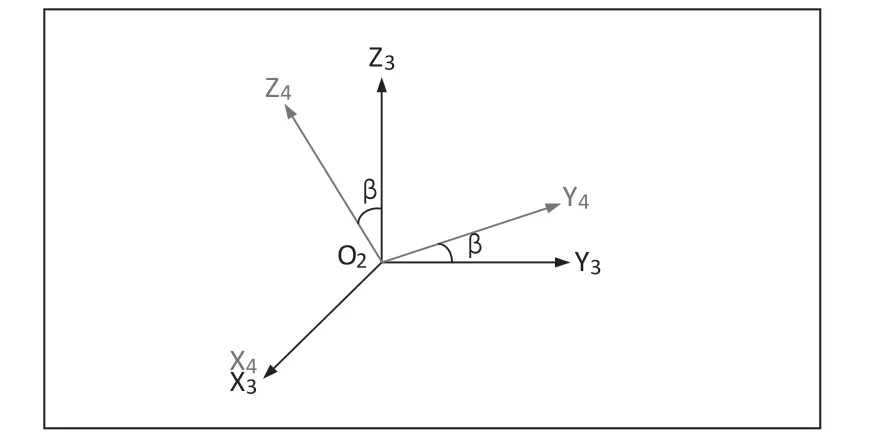
图3 O2—X3Y3Z3坐标系以O2—Y3 Z3平面旋转β得到O2—X4Y4Z4
i4、j4、k4为此坐标系下的正交单位向量。两坐标系的基矢量i4、j4、k4与 i3、j3、k3的关系为:

即:
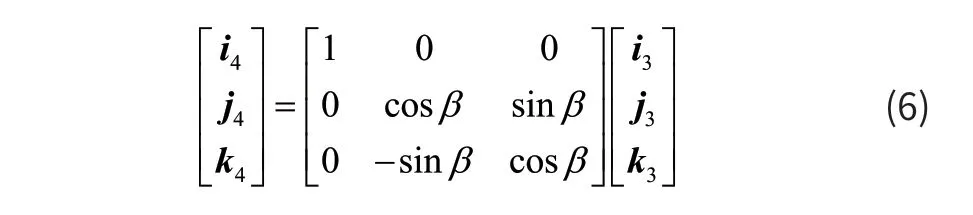

将O2-X4Y4Z4坐标系以O2-X4Z4平面旋转γ角度得到坐标系O2-X5Y5Z5,如图4所示。

图4 O2—X4Y4Z4坐标系以O2—Y4 Z4平面旋转γ得到O2—X5Y5Z5
i5、j5、k5为此坐标系下的正交单位向量。两坐标系的基矢量i5、j5、k5与 i4、j4、k4的关系为:
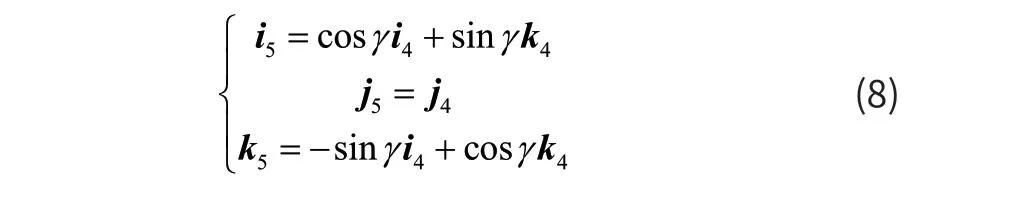
即:
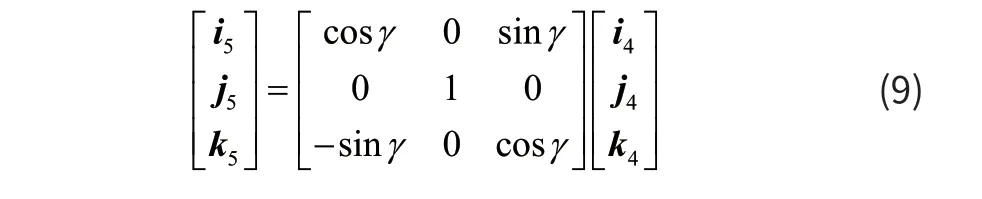

由(1)、(4)、(7)、(10)式可以得出:
2 光电观瞄器校正建模
对于遥控武器站而言,光电观瞄系统与枪架系统之间的相对连接多种多样,文中我们讨论两者完全独立时的光电观瞄器的校正[5]。如图5为某遥控武器站,车体前方为枪械武器系统,以枪塔耳轴轴线为X1轴,车体回转的耳轴轴线为Z1轴(此时枪塔角位移传感器读数为0),在两轴的交点处做两轴形成平面的法线,形成Y1轴,原点为O1;车体后方为光电观瞄系统,以其支架的耳轴轴线为X2轴,与车体之间的回转轴为Z2轴,在两轴的交点处做两轴形成平面的法线,形成Y2轴,原点为O2。

图5 遥控武器站及坐标示意图
观瞄器零位校正的基本方法是:首先在枪架上安装可见光的激光器(安装精准),在其前方放一个屏幕,此时激光器就会在屏幕上形成激光点P,P处于Y1轴上,距O1原点的距离为l1(未知),转动光电观瞄器,使其瞄准P点,原点O2与P1点之间的距离为L1(光电观瞄器上的测距机测得),观瞄器的方位角位移传感器输出的角度为α,俯仰角位移传感器输出的角度为β;假设光电观瞄器方位角位移传感器的零位相对于枪塔的方位角位移传感器的零位偏转∆1,光电观瞄器俯仰角位移传感器的零位相对于枪塔俯仰角位移传感器的零位偏转∆2,根据模型中的矢量关系建立方程,求出观瞄器的零位方位偏转角∆1和俯仰偏转角∆2。
如图6为建立的坐标系O1-X1Y1Z1,i1、j1、k1为此坐标系下的正交单位向量。然后建立O2-X2Y2Z2坐标系,i2、j2、k2为此坐标系下的正交单位向量。b,c为已知参数)。
假设O1-X1Y1Z1坐标系先平移得到O2-X2Y2Z2,然后O2-X2Y2Z2坐标系绕Z2轴旋转α+ Δ1 角度得到坐标系O2-X21Y21Z21,最后坐标系O2-X21Y21Z21绕X21轴旋转β+ Δ 2 角度得到坐标系O2-X3Y3Z3(α、β由光电观瞄系统的角位移传感器测得,为已知数),如图6所示,i3、j3、k3为此坐标系下的正交单位向量。则由1.2节可以得出:
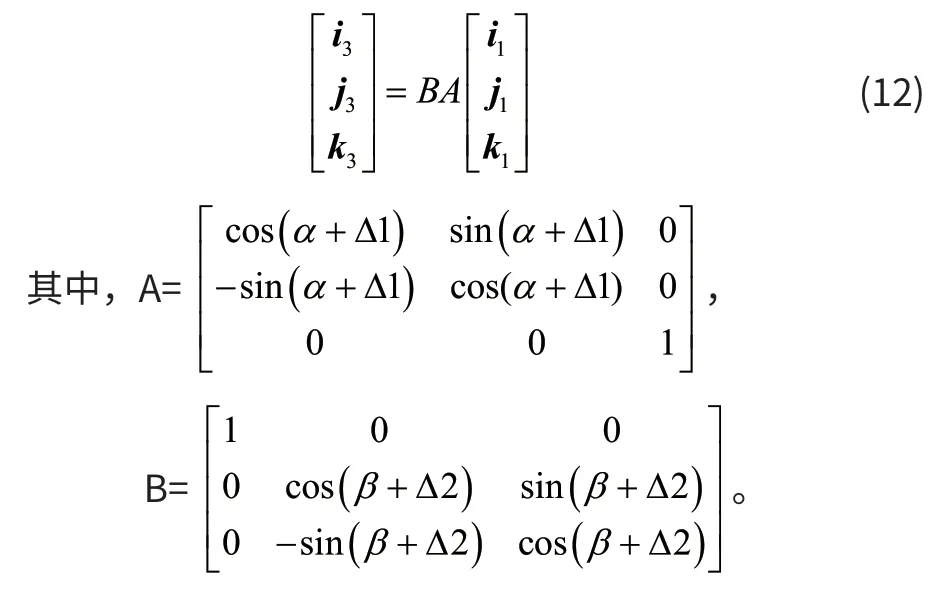
P1在O1-X1Y1Z1坐标系中的坐标为(0,l1,0),在O2-X3Y3Z3坐标系中的坐标为(0,L1,0),l1未知,由图6可以看出,即:
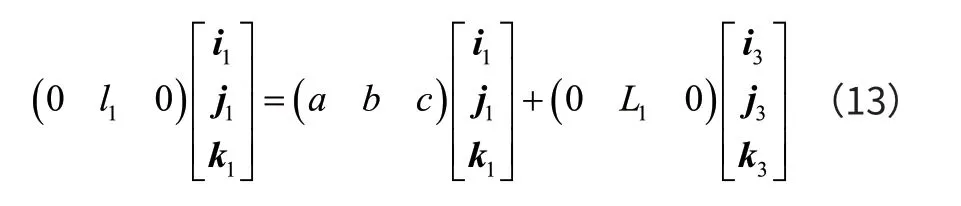
联立式(12)和式(13)可以得出:
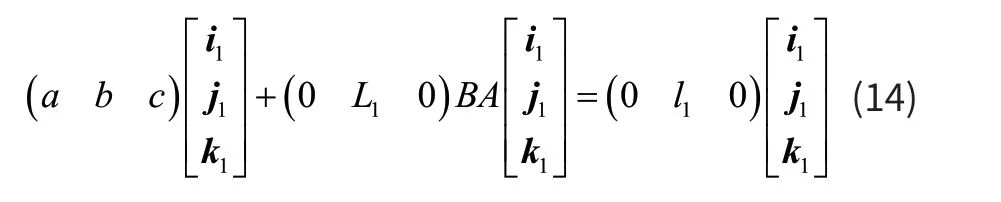
化简得:
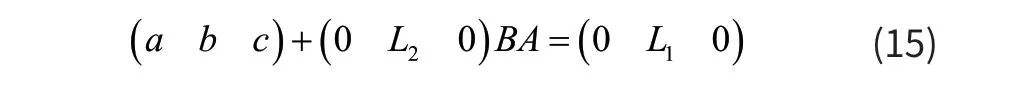
由式(15)可以得到:
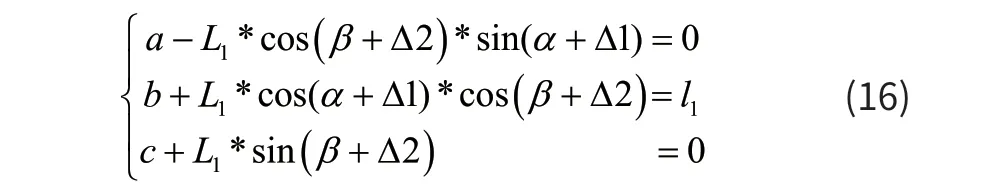
方程组有∆1、∆2、l1共3个未知量,α由观瞄器方位角位移传感器输出得到,β由观瞄器俯仰角位移传感器输出得到。以上3个方程求解3个未知数,解算上述方程组,就能够得到光电观瞄器相对于枪塔的方位偏转角∆1、俯仰偏转角∆2,然后进行观瞄器零位校正。
3 结果分析
在matlab中对上述数学模型进行程序编写,主要程序如下所示:
%根据建模得到的方程组进行计算
% 请输入观瞄器方位角位移传感器的输出值x1%请输入观瞄器俯仰角位移传感器的输出值y1(对应β):
%求解方程,求解光电观瞄器零位偏转角x(Δ1)、y(Δ2)等有关未知参数。

fprintf(‘光电观瞄器方位角位移传感器的零位相对于枪塔方位角位移传感器的零位偏转角度∆1= %11.10f ’,180/pi*x);
fprintf(‘光电观瞄器俯仰角位移传感器的零位相对于枪塔俯仰角位移传感器的零位偏转角度Δ2= %11.10f ’,180/pi*y);
fprintf(‘枪支距离目标P点的距离l1 = %11.10f ’,l1);
%**********注意程序里的角度都是弧度制,得转换成角度
利用C语言调用matlab程序,将封装好的程序写入单片机控制系统中,输入各项已知参数,改变屏幕的位置(即l1改变)进行多次试验,试验结果如表1所示。
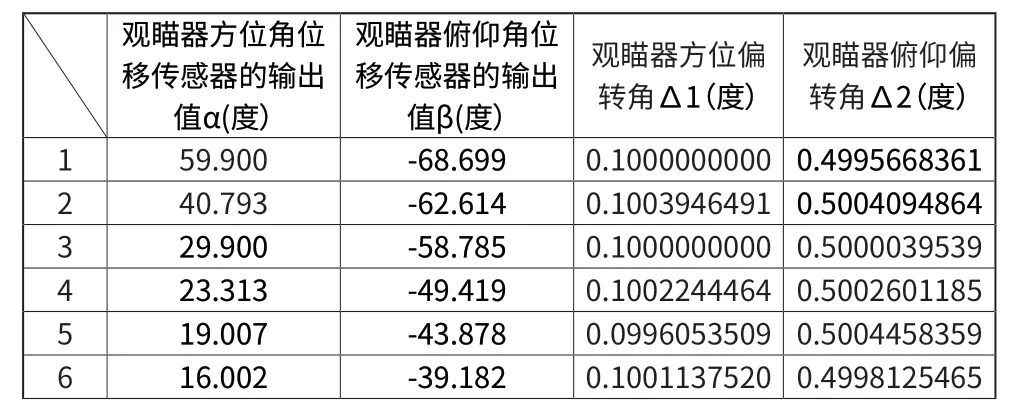
表1 试验具体数据
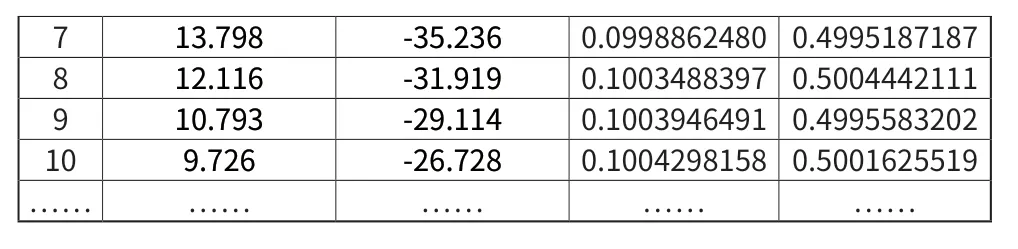
713.798 -35.2360.09988624800.4995187187812.116 -31.9190.10034883970.5004442111910.793 -29.1140.10039464910.4995583202109.726 -26.7280.10042981580.5001625519…… …… …… …… ……
由表1可以看出,改变屏幕位置,得到的观瞄器方位偏转角Δ1和俯仰偏转角Δ2基本相同,根据表1绘制出Δ1、Δ2的曲线图,如图7所示。
由图7可以得到,观瞄器处于零位时,其相对于枪塔的方位偏转角Δ1的最大误差为0.0009°,俯仰偏转角的最大误差为0.001°,符合试验要求,验证了该校正方法的准确性与可行性,为下一步试验的进行提供了重要基础。

图7 Δ1、Δ2的曲线图
4 结束语
本文采用空间坐标转换的原理研究了遥控武器站独立观瞄器的零位校正,设计了一种简便的观瞄器零位校正算法,进行校正的时候输入仪器测得参数,调用此算法,就能得到观瞄器的零位偏移角度,然后进行校正。
还需要注意,在使用以上算法时候,包含如下几个假设:
(1)枪塔回转轴角位移传感器的零点位置准确。
(2)枪管轴线与Y1轴(以枪架耳轴轴线为X1轴,与车体的回转轴为Z1轴(此时角位移传感器读数为0),两轴相交垂直且形成Y1轴,Y1轴与两轴相垂直。)是重合的,假如不重合,可以再建立一个坐标系,此坐标系的三个轴线分别与O1-X1Y1Z1坐标系的三个轴线平行,且方向相同,然后利用坐标转换关系进行计算。
(3)光电系统的光学轴线与Y2轴(以光电观瞄系统支架的耳轴轴线为X2轴,与车体之间的回转轴为Z2轴,两轴相交垂直,做Y2轴,Y2轴与两轴相垂直。)是重合的,假如不重合,可以再建立一个坐标系,此坐标系的三个轴线分别与O2-X2Y2Z2坐标系的三个轴线平行,且方向相同,然后利用坐标转换关系进行计算。
如果想要继续进行深入研究,则(1)、(2)、(3)假设都不成立,这样就会使得观瞄器的零位校正变得更为复杂,可以作为下一步的研究内容。
