第一类Fredholm积分方程分段泰勒级数展开法
2022-02-16刘雪铃
刘雪铃, 黄 静
(亳州学院 电子与信息工程系, 安徽 亳州 236800)
0 引言
1782年Laplace提出的Laplace逆变换以及1811年Fourier提出的Fourier反演问题, 都属于积分方程[1]. 而近年来, 随着社会的飞速发展, 积分方程在数学、 物理等领域扮演着愈发重要的角色, 引起了学者们的广泛关注[2-5]. 随之而来的关于积分方程的数值求解也显得格外重要. 对于一维的Fredholm积分方程和Volterra积分方程, 国内外学者也进行了大量的研究. 文献[6]利用再生核, 构造了Fredholm积分方程的Hermite数值解, 并证明解的存在唯一性. 文献[7]利用光滑化方法给出第一类Fredholm积分方程的稳定数值解, 并通过数值算例表明该方法的有效性文献[8]利用Legendre小波函数获得了第一类Fredholm积分方程的数值解, 关于这方面的成果可见文献[9-11]. 文献[12]利用泰勒展开式得到第二类Fredholm积分方程的数值解并证明了解的存在性. 受到以上内容的启发, 本文利用泰勒展开式得到了第一类Fredholm积分方程的数值解, 并通过数值实例来证明方法的可行性与有效性.
1 分段泰勒级数展开法
一般来说, 第一类Fredholm积分方程可以写成

(1)
这里的f(x)为定义在区间[a,b]上的已知连续函数,φ(t)是未知函数. 接下来, 我们有两种数值方法, 一种是对(1)式进行积分, 另一种方法是对(1)式进行微分. 为了方便起见, 我们把前者称为积分法, 后者称为微分法.
1.1 积分法
接下来, 我们对(1)式进行i(i=1,2,…,m(n+1)-1) 次积分可得:
(2)
对(2)式交换积分顺序
(3)
为了书写方便我们有以下假定:
(4)
(5)
则(2)式和(3)式可以表示为
(6)
其中i=1,2,…,m(n+1)-1. 下面选择一系列的间断点a=x0
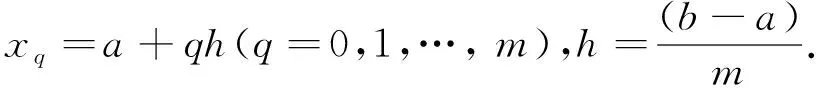
则(6)式可以表示为
(7)
式(7)中的φ(t)可以表示为带有拉格朗日余项的泰勒级数展开式, 即可得到
(8)
将(8)式代入(7)式可得
(9)
(10)
此外
(11)
其中
(12)
(11)式可以写为:
LΦ=F
(13)
(14)
(15)
根据著名的克拉默法则, 我们知道这个方程组的解:
其中矩阵Lq(x)代表矩阵F(x)替换矩阵L(x)的第q列.
1.2 微分法
与上面的方法相反, 若K(x,t)和f(x)对变量x具有i(i=1,2,…,m(n+1)-1)阶导数, 我们对(1)式进行i(i=1,2,…,m(n+1)-1)次求导可以得到
(16)
和上面的积分方法相同, 我们对(1)式和(16)式中未知函数φ(t)进行泰勒展开, 类似(13)式可以得到:

(17)
其中
(18)
(19)
(20)
同样借助克拉默法则, 我们可以得到方程组(17)的解:
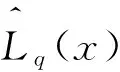
2 例题
为了表明上述方法的可行性, 首先我们将会给出一个例题用上述的方法进行求解, 其次用其他文献中的方法去求解这个例题, 同时给出数值解与精确解的绝对误差.
例:考虑下面第一类Fredholm积分方程
其中0 为了显示该方法的可行性, 我们选择文献[13]中的方法, 取n=4可以得到方程的近似解, 对本文中的方法, 我们选择(m,n)=(2,4),(m,n)=(4,4)和(m,n)=(8,4), 求得方程的数值解与精确解的绝对误差, 可以得到表1. 表1 数值解与精确解的绝对误差 从上面表格中的数据可以看出本论文提出的方法是可行的, 并且对比其他文献中的数值求解方法更加精确. 使用本文中的方法只要m,n选取合理, 就能得到比较精确的数值解. 本文研究了第一类Fredholm积分方程的数值求解, 基于积分方程理论和泰勒展开式等, 建立了等价的积分方程, 而且利用积分法和微分法, 求解出方程的数值解, 通过数值例子验证了所得结果的可行性与有效性.
3 结论
