基于三维误差空间模型的阴极板垂直度检测方法

袁 峰

（江西瑞林装备有限公司，江西 南昌 330032）

随着我国铜冶炼行业的蓬勃发展，21世纪的中国已成为世界铜矿产量第二，炼铜产量第一的大国，永久阴极电解法（简称ISA法）工艺和铜湿法电积（电解）已广泛应用，不锈钢阴极板在铜电解生产中也随之大量使用，但在铜电解生产过程中，有多种原因会导致不锈钢阴极板变形，如不锈钢阴极板反复收到机械装置的挤压导致反复弯曲、工人在装夹边条的不当操作、不锈钢阴极板在行车吊装等过程中，随着时间的积累，不锈钢阴极板的垂直度会超出工艺技术要求，而阴极板的垂直度对保持电流的均匀分布及电流效率作用极为重要。阴极板的平直不容易发生短路，故可采用较小的极距和较高的电流密度，从而提高生产效率嘲；而垂直度差的阴极板则会导致电流分布不均，严重时会产生电流短路和析出阴极铜的质量缺陷，不但影响阴极铜质量，而且易与阳极板接触出现短路，从而造成经济损失和能源损耗。因此，在阴极板脱铜后，对其平整度进行检测，在下一电解流程之前，将平整度不够的阴极板剔除，保证进入电解槽所有极板的平整度均达标，这一过程十分重要[1]。目前检查不锈钢阴极板垂直度好坏的问题，大部分都是靠人工经验看或通过测量工具来人工测量；为了保证阴极铜的质量和良好的电解技术经济指标，能准确快速和便的检测出垂直度差的不锈钢阴极板，设计了一种运用三维空间模型的思路（三维误差空间模型的阴极板垂直度检测方法），避免检测过程中阴极板的各种运动因数的影响。

1 控制对象系统分析

目前，国内外对板面平整度的检测主要分为两大类：接触式检测和非接触式检测。对于接触式检测，使用金属探针接触板面进行检测；对于非接触式检测，运用光的反射原理进行检测。这两种检测方法存在以下问题：

（1）当采用接触式检测时，待检测的阴极板在完成脱铜后并不是静止不动的，采用金属探针接触时，容易对板面造成刮伤，降低阴极板的使用寿命，同时，运动中的阴极板容易将金属探针损坏。

（2）当采用非接触式检测时，运用光的反射原理判断阴极板平整度，当极板处在晃动状态，光学探头对反射光的接收存在偏差，虽然可以避免接触式检测的问题，但检测误差很大，无法达到检测要求[2]。

现在的研究是基于三维误差空间模型的阴极板板面平整度检测的方法，其特征在于采用非接触式检测手段，通过9个超声波传感器检测待测板面，且使9个检测点均匀的分布于整个检测面；选取所测数据中三个不共线的点，确定一个恰好能使待测面在所得面一侧的面，根据设定的平整度允许最大值，通过空间坐标运算求得另一平面，因此，夹在所得的两个面之间的区域即为该检测板面的平整度误差空间；通过所得的两个面可以求得其余6个点允许的测量值范围，通过判断实际测量值是否在允许的范围内即可判断该板面是否符合平整度的要求[3]。该方式的优点是：采用非接触式检测手段，不会对检测板面造成不必要的损伤、采用超声波传感器进行测量，其很好的穿透性能够有效的避免检测环境对最终检测精度的影响、采样阴极板在运动中某一时刻的数据确定误差空间模型，然后判断该时刻的数据是否满足要求。这样无论阴极板如何晃动或者晃动的幅度和频度多大，均可达到精确判断的效果。

2 系统控制设计及其模型

针对三维误差空间模型的阴极板板面平整度检测的硬件配置，控制面板、CPU处理器，超声波等，采集、数据的滤波等都是通过CPU处理器实现的，其组态结构如图1所示：

图1 控制硬件示意图

该系统采用9个超声波传感器，如图2所示，等距均匀的安装在恰好能覆盖待检测阴极板板面的XOY平面上。

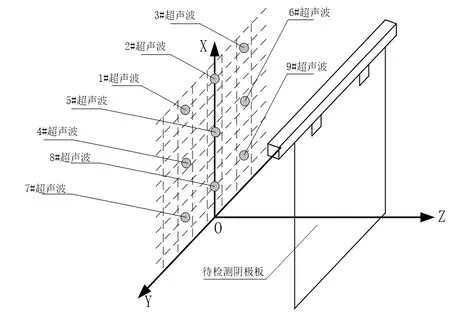
图2 控制硬件示意图

新型原理框如图3，构成数据采集单元（1），由机械安装尺寸可知其X坐标值和Y坐标值。数据采集单元（1）的9个采样数据，即为在检测板面上检测点的Z坐标值，经过数据筛选单元（2），选出其中Z坐标值最小且不共线的三个点。

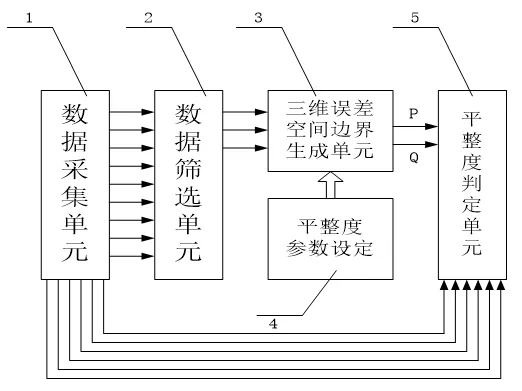
图3 新型原理框图

由上述描述的这三个点，经过空间坐标运算，确定过这三个点的平面P，即三维误差空间模型的最靠近传感器一侧的边界面，如附图4，该平面恰好使检测板面处于其右侧（只是相交于选出的3个点）；根据平整度参数的设定和上述边界面P，可以确定另一边界面Q。边界面Q的特点为：平行于边界面P，且沿Z轴正方向与边界面P之间的距离为所设平整度允许值。因此，三维误差空间模型的边界面已确定。最后将其余的6个点的X,Y值分别代入边界面P、Q的方程中，确定每个点Z值的允许范围，最后判断实际的测量值是否在相应的区间范围内，作出最终平整度的判断。本实用新型通用性强，无论阴极板如何晃动，或者检测时未能与传感器安装面平行等各种复杂情况下均可准确判断检测极板的平整度是否满足要求。

图4 三维误差空间模型

3 三维误差空间模型的设计

为此，本实用新型提出一种基于三维误差空间模型的极板平整度检测方法。该方法采用9个超声波测距传感器，分别检测阴极板距传感器的距离，然后建立直角坐标系，通过三维空间坐标运算，根据板面平整度的范围要求，定位某一瞬间待检测阴极板平整度的误差空间，最后通过判断实际检测到的数据是否处于该误差空间来判定阴极板平整度是否达标。

如图2，为检测区域示意图，当安装位置确定后，9个传感器在直角坐标系中的X，Y值可以根据机械安装尺寸得知。当阴极板运动到检测区域时，传感器测量阴极板某一运动状态下的9个值，因此，9个检测点的在直角坐标系中的Z值也已知。所以，可以得到9个检测点在直角坐标系中的坐标。

在这9个点中，选取Z值最小的3个点(此三点在XOY平面不共线)，确定一平面P，可得出其平面方程为：AX+BY+CZ+D1=0。则该平面为在检测板面一侧，且恰好与检测板面相交的面（结合处为点，并非交叉相交），将这个面作为误差空间模型的边界面之一；假如允许的极板平整度最大为d，则可以认为，误差空间模型的另一边界为沿Z轴正方向，平行于平面P，且距离为d的平面，设为Q。则可以根据以上条件计算出平面Q的方程为：AX+BY+CZ+D2=0。这样就确定了误差空间的模型 ，如图4。

将剩下的6个点的X值与Y值代入误差空间模型的两个边界面方程可以得到每个检测点z值的允许范围，最后判断实际测量的每个z值是否在相应的z值允许范围内，若在，则板面合格；反之，不合格。

具体实施方式：

（1）将板面多点检测装置（本实例中为9个点，分别是板面的左上、左中、左下、正上、正中、正下、右上、右中、右下，此处分别给其下定义A1、A2、A3、A4、A5、A6、A7、A8、A9点）安装在需要检测装载板的工位一侧（此处以B面为例），确保多点检测装置的每一点均能正确检测到板面的相应位置[4-6]。如图5所示。

（2）安装后，以板面多点检测装置上的某一个点为原点（不要以检测点作为原点），做空间三维坐标XYZ轴。本方案中，以与板面平行的面做平面XY轴，以与板面垂直的面做三维空间Z轴，其中：设定X轴为横向水平，正向方向为面向A面朝右；设定Y轴为纵向垂直，正向方向为垂直向上；设定检测装置往板面位置方向为Z轴正向。测量出每一个检测点的XY轴坐标，并记录下相应点的XY轴坐标值。如图6所示。

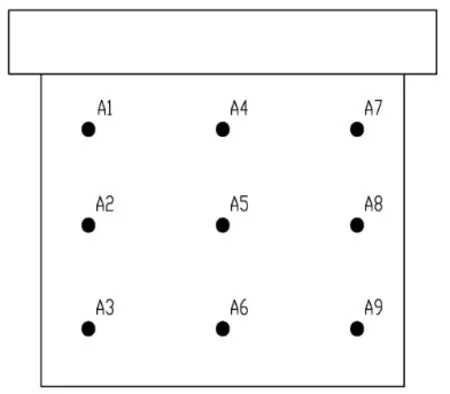
图6 多点检测装置检测点

（3）找一块参照装载板，放在检测的工位上，按照多点检测装置中每一个检测点的位置，将此参照装载板的每一个检测点的垂直度数值人工检测出来，垂直度检测的面需与板面多点检测装置在同一侧，然后记录下对应点的测量值。

（4）通过工业可编程控制器读出通过超声波传感器测出的此参照装载板每一个检测点的值，并记录下来对应点的测量值。根据（3）中的人工测量出来的垂直度值进行比较和纠差，例如人工测量标准值为15mm，A1点人工测量值为13.2mm，则，A1点的参考传感器测量值则在实际传感器的测量值的基础上加上（13.2mm～15mm）的纠正值。以此为例，依次记录下计算后的每一个检测点参考传感器测量值。如图1所示。

（5）检测工位放上一块实际使用装载板，将实际使用装载板的实际检测值减去（4）中记录下来的参考传感器测量值，得出实际使用装载板的相对传感器测量值，此值即为实际使用装载板的Z轴值。如图5所示。

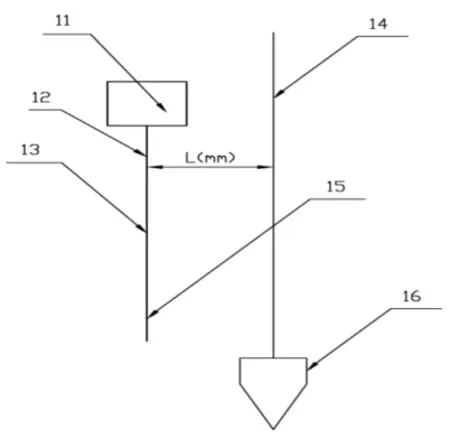
图5 板面多点检测装置

（6）将每一个测量点的三维空间Z轴值，在PLC中通过冒泡法从小到大排序，取Z轴值最小的三个测量点，假设为M1(X1，Y1，Z1)，M2(X2，Y2，Z2)，M3(X3，Y3，Z3)。判 断 此三个点是否成一条线，若成线，则取测量值第一，第二，第四小的三个测量点。将此三个点的三维空间坐标值确定一个三维空间数学面，公式如下：

AX+BY+CZ+D=0

其中：

A=Y2Z3-Y2Z1-Y1Z3-Y3Z2+Y3Z1+Y1Z2

B=X3Z2-X1Z2-X3Z1-X2Z3+X2Z1+X1Z3

Z=X2Y3-X2Y1-X1Y3-X3Y2+X3Y1+X1Y2

D=X1Y3Z2-X1Y2Z3+X2Y1Z3-X2Y3Z1+X3Y2Z1-X3Y1Z2

以此面为基准面去判断其余6个点距离这个数学面的垂直距离，公式如下：

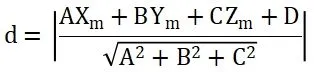
其中Xm，Ym，Zm表示第m个点的三维坐标，只要存在一个点的垂直距离d大于设定值，则说明此实际使用装载板垂直度不符合要求。

此方法可成功排除掉人工安装导致的传感器放位不准，检测工位放板位置不准和参考板并不标准等外在因素。对于设备安装要求大大降低，符合实际工程施工环境，同时大大提高测量精准度和普及度。