企业原材料订购与运输决策模型

朱隆吉

（西北大学信息科学与技术学院，陕西 西安 710127）

0 引言

在市场经济环境下，某建筑和装饰板材的生产企业所用原材料大致可分为A、B、C三种类型。该企业每年按48周安排生产，需要提前制定24周的原材料订购和转运计划：根据产能要求确定原材料的供应商和相应每周的订货量，进而选择合适的转运商。本文先从已有的402家原材料供应商中选定最重要的50家，进而确定最经济的订购方案和损耗最少的转运方案，实现企业经济效益最大化。

1 数据来源与模型假设

（1）假设在通常情况下，每家供应商每周供应的原材料只由一家转运商进行运输。

（2）为简化计算，假设三类原材料运输和储存的单位费用相同且等于1。

（3）不考虑转运商前往供货商所在地接收原料的成本。

2 供应商评价模型建立和求解

2.1 供货特征指标选取和指标评价体系构建

从402家原材料供应商的订货量和供货量数据中提炼出衡量供应商供货特征的指标，进而根据特征指标建立数学模型来反映不同供货商对保障企业生产的重要性。笔者考虑从供货稳定性、竞争能力、生产能力三方面来分析影响供货特征的指标。

2.1.1 生产能力

（1）实际周均供货量Si。

（2）技术水平Techi。

2.1.2 竞争能力

（1）订单获得率Mi。

（2）订货量占有率Ki。

2.1.3 供货稳定性

（1）供订差异水平Dfi。

（2）交货违约率Ri。

2.2 基于TOPSIS方法的供货特征量化模型

依据上文所计算的各项指标数值及评价体系，考虑建立基于TOPSIS方法的供货特征量化模型[1]来量化供货特征，反映各供应商对企业保障生产的重要程度。首先，要确定各项指标的权重，为避免主观因素对于量化结果的影响，考虑使用熵权法对各项指标进行赋权。得到各项指标的权重后，使用TOPSIS方法来量化分析供应商的供货特征。

2.3 模型的求解和结果

运用MATLAB软件编程，计算6个特征指标的权重，计算结果如表1所示。

表1 各特征指标权重

然后，借助已计算出的特征指标权重，使用TOPSIS方法计算各供应商的生产保障得分，由此确定50家最重要的供应商。

3 订购-转运决策模型建立和求解

3.1 基于0-1整数规划的最少供应商数量确定

要在已确定的50家最重要供应商中选择满足企业生产的最少供应商数量，对于生产企业来说，供应商的选择与否关乎企业一周内可以得到的供应量的大小和稳定性，进而直接影响企业的产能和生产需求。为此，引入0-1逻辑变量[2]来表示是否选择第家供应商来供应原材料，设0-1变量：

3.1.1 决策变量

本题的思路围绕是否选择供应商展开，考虑将0-1变量ai作为问题的决策变量。

3.1.2 目标函数

要得到满足企业生产的最少供应商数量，故把最少供应商数量作为模型的优化目标，则优化目标为：

3.1.3 企业产能约束

要求尽可能少选择供应商数量来满足企业的生产需求，意味着被选择的各类原材料供应商的总供货量与单位产品消耗原材料的比值应不小于企业当周产能，因此有如下约束条件：

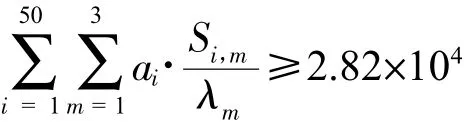
其中，Si，m表示生产m类原材料的供应商的周均供货量，m=1，2，3分别对应A、B、C三类原材料供应商；λm表示生产每立方米产品需要消耗的第m类原材料数量。

3.1.4 基于0-1整数规划的最少供应商模型的建立

综上，结合下式，可以建立基于0-1整数规划的最少供应商模型：

3.1.5 模型求解和结果

基于所建立的模型，使用MATLAB求解，得到满足企业生产需求的最少供应商数量为22家，供应商的编号和生产原材料类型如表2所示。

表2 满足企业生产需求的供应商

3.2 模型的求解

使用Lingo软件编程得出每周的最小总成本和企业对各供应商的订购量，限于篇幅本文仅列出编号为S395、S361和S282等三家供应商在未来24周的最优订购量，如图2所示。

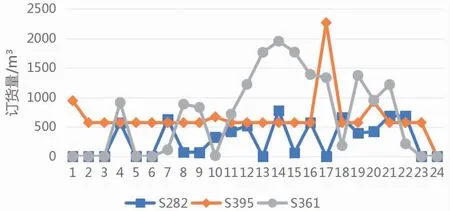
图2 三家供应商在未来24周的最优订购量

3.3 基于0-1整数规划的转运决策模型

3.3.1 模型的建立

要制订损耗最少的转运方案，在实际转运过程中，原材料总会有一定的损耗，但是各转运商的转运原材料的损耗率是各异的，如何选择合适的转运商运送原材料使得原材料的总损耗量最少是解决问题的关键。显然这仍是一道优化问题，最少损耗量是最终的优化目标。此外在前文已建立的订购决策模型的基础上，可以得到企业在未来24周中对各供应商的订货量，但转运商的选择仍为未知量。为此，考虑建立目标规划模型求解。

为简化问题，假设每家供应商每周供应的原材料只由一家转运商进行运输，故引入0-1逻辑变量来表示第家供应商是否选择第家转运商来供应原材料，则设0-1变量其中，和分别表示供应商编号和转运商编号。

（1）决策变量

本问的解题思路基本上是围绕如何选择转运商而展开的，考虑将0-1变量作为问题的决策变量。

（2）目标函数

本小问要求制订损耗最少的转运方案，故把最少损耗量作为模型的优化目标，则优化目标为：

式中：Y表示每周运送原材料的总损耗量；Ej表示第j家转运商运送原材料的损耗率；ai·Gi，m（k）反映第家供货商的供货量。

（3）约束条件

①运输能力约束。

依题意可知，每家转运商的运输能力为6 000立方米/周，即有如下约束条件：

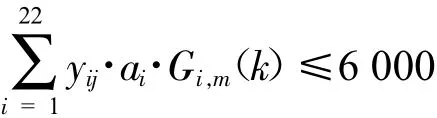
②转运商约束。

为简化问题，假设每家供应商每周供应的原材料只由一家转运商进行运输，则满足约束：

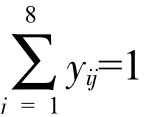
3.3.2 模型的求解

基于所建立的模型，求解得到每周损耗量最少时的转运商选择方案，进而可得到各转运商每周的转运量，限于篇幅本文仅列出编号为T3、T5和T6三家转运商在未来24周的最优转运量，如图3所示。

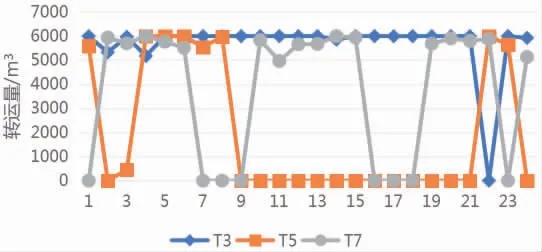
图3 三家转运商未来24周的最优转运量

4 结语

本文量化分析供应商的供货特征时，选取的指标覆盖了供货商的多方面的数据，能较为全面地反映供货商的实力。基于TOPSIS方法的供货特征量化模型也对供货商的重要程度做出精确的打分。基于规划模型的订购—转运方案考虑了多方面的成本，约束条件设定较为合理，并且运用离散时间下的动态规划进行求解，能精准制订最经济的订购方案。现实生活中生产企业根据该问题的模型综合考虑，制订最经济的订购方案和损耗最少的转运方案，实现企业经济效益最大化。