两类供应风险下装配商的最优订购策略
2022-02-16吉清凯胡祥培
吉清凯, 胡祥培, 赵 达
(1.海南大学 管理学院,海南 海口 570228; 2.东南大学 经济管理学院,江苏 南京 211189; 3.大连理工大学 经济管理学院,辽宁 大连 116024)
0 引言
随着外包的盛行与供应链的延伸,制造企业面临越来越多的供应风险(如日本地震导致的汽车零部件供应中断,手机关键零部件良品率波动,OLED供应商产能不足等。供应风险下的供应链管理已成为业界与学术界共同关注的热点。对于产品包含许多零部件的装配制造企业而言,其面临的供应风险种类更多、频率更高,并且在零部件互配性(零部件缺一不可)的作用下,供应的风险将被放大。因此,如何在多类供应风险下合理计划采购是装配制造商面临的亟待解决的难题。
具体而言,在装配制造中,有些核心零部件涉及诸多新技术、新设计与新工艺,往往存在良品产出率随机的问题,比如苹果手机iPhone 5曾因为其in-cell触控屏供应商良品率过低而出现缺货。有些非核心的零部件也可能会出现产能不确定的情况,如HTC One Mini曾因外壳产能不足导致发布延迟而错失销售良机。iPhone X在上市前则同时遭遇NAND闪存产能不足和OLED面板良品率低的双重风险。对于这两类供应风险,装配商和供应商都不愿囤积库存来应对。这是因为创新型电子产品更新换代快,零部件易过时,库存呆滞的风险极高(如iPhone X上市后销售不畅,导致零部件库存量高达实际出货量的3倍)。此时,装配商的零部件订购决策变得极为重要,但也比较复杂。目前已有一些供应风险下装配系统的订购/库存决策研究(如Li与Arreola-Risa[1],吉清凯等[2],以及Tajbakhsh等[3]的综述),为本文提供了可借鉴的理论和方法,但这些文章都只考虑单一类别的供应风险。当面临多类不同的供应风险时,装配商的最优订购策略具有什么结构?不同类别的供应风险在零部件互配性的作用下如何影响最优订购决策?
针对上述研究问题,本文考虑零部件供应面临不确定产能和随机产出率的风险,建立零部件订购的随机非线性约束规划模型,基于约束极值理论刻画出最优的零部件订购策略,并对不同种类的供应风险的影响展开分析,为装配商提供科学的辅助决策工具与有益的管理启示。
关于供应风险下的订购/库存决策有许多研究,其中与本文比较相关的是针对装配系统研究。Xiao等[4]刻画装配产能不确定风险下的最优预装配量、零部件预存量以及追加装配量,探讨按单装配与预装配混合策略的优越性,但其未考虑零部件供应的风险。Ji等[5]假定n个零部件均具有产能不确定性,刻画了装配系统的单周期最优订购策略,但其模型中的零部件供应风险是同类型的。DeCroix[6]刻画了中断风险下装配系统的多周期最优库存控制策略,同样,其模型中零部件的供应风险也是同类型的。Bollapragada等[7],Bollapragada等[8]假设装配系统按基本库存(Base-stock)策略运行,寻找产能不确定风险下的最优策略参数并考察系统的表现,与之关注的焦点不同,本文着重于最优策略结构的刻画。Güler与Bilgic[9]与Li等[10]设计基于惩罚的契约以协调随机供需下的供应链,二者的区别在于分别考虑“被动顺从”与“自动顺从”(即上游是否严格按下游的订单安排生产)。Li等[11]考虑一个装配商与两个供应商组成的装配系统,假设供应商1面临供应中断风险,而装配商与供应商2可协助其进行产能恢复,研究其中的供应链协调机制。这三篇文献关注一类供应风险下的供应链协调问题,本文关注多类供应风险下的最优订购策略问题。Wang与Gerchak[12]曾刻画了不确定产能与随机产出率双重供应风险下单个零售商的最优库存策略,但其结论较难扩展到包含多个零部件的装配系统中。
可见,多个零部件面临不同类供应风险条件下装配系统的运营优化问题仍有待深入研究。在装配系统中,由于存在零部件互配性,所以零部件订购决策天然存在着紧密联系,而不同类别的供应风险对订购决策的影响不同,导致不同零部件的供应风险相互作用,终将使得零部件的订购决策变得更加复杂。本文研究将有助于丰富供应风险下装配系统运作管理领域的理论研究,且有利于指导企业的采购管理实践。
1 问题描述与假设
考虑一个装配制造企业,其采购两种零部件(零部件1与2,分别由供应商1与2提供)并按1:1的比例组装成1单位的最终产品以满足某个销售周期的市场需求。零部件1是一种采用成熟技术的标准件(如智能手机的塑料件或普通金属部件),其生产制造难度不高,供应商1可使用已有设备进行生产。但是由于已有设备偶然的停机、检查、维修等原因,零部件1周期内的生产能力具有不确定性,具体表现为:供应商1在周期内计划生产u单位,将只有min{u,K}单位的产出,其中K是周期内不确定的产能。零部件2是一种采用了新材料或新技术的非标准件(如高端智能手机的屏幕),其生产制造难度高,尽管供应商2已购进新设备并投入了充足的产能,但是仍存在较多次品,即零部件2具有随机产出率,具体表现为:供应商2周期内计划生产u单位,将只有ξu单位的产出,其中ξ∈[0,1]是随机产出率。假设装配商知晓零部件1与2的供应不确定性,即其掌握K与ξ的具体分布,而供应商将按照装配商的订购量安排生产。本文关于不确定产能与随机产出率的模型描述与上一节中相关文献(如Xiao等[4],Ji等[5],Wang与Gerchak[12])的描述相同,不同之处在于本文假设一个装配系统中同时存在这两类供应风险。
令ci表示零部件i=1,2的单位购入成本。将最终产品的销售价格(给定的外生变量)规范化为1元,且假设总购入成本小于销售价格,即∑ici≤1。组装成本与零部件残值均设为零(Gerchak与Wang[13]在关于一般装配系统的研究中也作相同假设,可以根据第3节的方法证明本文结论在非零组装成本和残值假设下也成立)。令F(·)和Q(·)分别表示K与ξ的累积分布函数,假设其递增且二次可微。变量符号及其含义如下所示。

符号含义K零部件1的不确定产能F(·)K的累积分布函数,支撑集为(0,∞)定义F(·)=1-F(·)ξ零部件2的随机产出率Q(·)ξ的累积分布函数,支撑集为[0,1]定义Q(·)=1-Q(·)μξ的均值ui零部件i=1,2的订购量ci零部件i=1,2的单位购入成本D最终产品需求预测值(u∗1,u∗2)最优的零部件订购量
装配商对最终产品的销售预测值为D,装配商的期望利润函数为
Π(u1,u2)=E[min{u1,K,ξu2,D}-
c1min{u1,K}-c2ξu2]
(1)
其中E表示对所有随机变量(即K与ξ)取期望,而min{u1,K,ξu2}代表最终产品的数量。不难发现,若考虑零部件i=1,2的缺货惩罚成本pi,则装配商的期望利润函数变为Π(u1,u2)=E[min{u1,K,ξu2,D}-(c1+p1)min{u1,K}-(c2+p2)ξu2+∑ipiui]。与(1)式比较,可见考虑缺货惩罚成本并不会改变装配利润函数的结构,反而使函数形式变复杂了。故在下文不再考虑缺货惩罚成本,以(1)式为装配商的期望利润函数。
显然,零部件1的订购量不应大于D,故装配商的问题变为

c1min{u1,K}-c2ξu2]}
(2)
2 问题求解与分析
2.1 最优订购量决策
尽管min{u1,K,ξu2}是关于(u1,u2)的凹函数,但由于-c1min{u1,K}是u1的凸函数,故Π(u1,u2)在定义域+上不是关于(u1,u2)的凹函数,但是,能够证明如下引理成立。
引理1在区域Z={(u1,u2)|0≤ui,i=1,2,u1≤Q-1(1-c1)u2}内,Π(u1,u2)是关于(u1,u2)的凹函数。

(3)
(4)
命题1为采购经理提供如下两条容易理解与操作的管理规则:
推论1零部件1的最大订购量是需求预测值D,但零部件2的最大订购量是需求预测值的固定倍数(即D/Q-1(1-c1)),该倍数取决于零部件1自身的成本和零部件2的产出率分布。
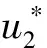
2.2 灵敏性分析
在实际中,产出率一般会随着制造企业对新技术、新材料的学习曲线随机地增大,而设备的产能一般会随着预防性维护、流程改进等的投入而随机地增大。为了考察多种供应不确定性对零部件最优订购量的影响,本节利用一阶随机占优的概念来对供应不确定性进行灵敏性分析。




3 数值实验
本节通过数值实验来验证上文中已被证明的结论,并进一步直观地考察多类供应风险对最优订购量的影响。
3.1 参数设置
因为零部件2采用了新材料或新技术,故其可能比零部件1更昂贵,所以假设购入成本为c1=0.1
3.2 结果分析


图1 λ变动时最优订购量决策及利润的变化

图2 κ变动时最优订购量决策及利润的变化

分析根据定义1,当λ增大(保持κ=5)或κ增大时(保持λ=5)时,零部件1的产能随机增大(对∀x∈[0,1],F(x)变小),此时,采购经理调高零部件1的订购量,其期望进货量也将增大,相应地,零部件2的订购量和期望进货量也增加,从而装配商的利润也增大。此结果与命题2。(i)结论一致。
接下来变化ξ~Beta(α,β)的参数以观察零部件2的产出率变化时的影响。

图3 α变动时最优订购量决策及利润的变化

分析根据定义1,当α增大时,零部件2的产出率随机增大(对∀x∈[0,1],Q(x)变小),此时,采购经理在保证零部件2的期望产出量有所增大的前提下可减小其订购量(即结果(i))。相应地,零部件1的订购量也应有所增大以匹配零部件2的期望增量,但是,α增大也使得零部件2的随机产出率的方差下降,从而零部件1的不确定产能逐渐成为主要的供应风险,最终导致采购经理调低零部件1的订购量以避免其过剩的风险(即结果(ii))。这一结果与命题2(ii)中的结论不同,其原因是Beta分布并不总能满足命题2(ii)中要求的“q(·)是非减函数”条件。不过,零部件2的产出率随机增大总是使得装配商的利润增大。

图4 β变动时最优订购量决策及利润的变化

分析根据定义1,当β增大时,零部件2的产出率随机减小(对∀x∈[0,1],Q(x)变大),此时,为了保证零部件2的进货量,采购经理可适当提高零部件2的订购量,但其期望进货量仍将会下降(即结果(i))。此时,采购经理也有必要调高零部件1的订购量以匹配零部件2订购量的增大。但是,零部件1的订购量不会先增后减。这是因为,虽然β增大使得零部件2的随机产出率的方差下降,但由于零部件2的产出率整体而言随机地减小,所以零部件1的不确定产能不会变成主要的供应风险,从而采购经理能够有信心调高零部件1的订购量。最后,尽管产出率的稳定性提升(方差减小)一定程度上有助于进货量的提升,但由于产出率均值减小,装配商的利润还是一直在减小。结果2与3说明了零部件随机产出率对订购决策的影响更加复杂。
根据以上结果可见,零部件1的产能随机增大与零部件2产出率随机增大均利于装配商,但两种情况下的最优订购量的变动有较大的不同,零部件1的产能随机增大使得装配商同时调高两种零部件的订购量,并且装配商的利润单调上升,而零部件2产出率随机增大使得装配商调低零部件2的订购量,但零部件1的订购量或增或减,装配商的利润则单调上升。本文的结论与分析对采购经理者进行供应商管理(如帮助供应商提高零部件1的产能或控制零部件2的产出率)和采购计划有一定的指导意义。
4 结语
本文研究两类供应风险下装配系统中零部件的最优订购策略问题。考虑包含两个零部件的装配系统,其中,零部件1是一种标准件,但由于设备停机、检查、维修等原因,其产能具有不确定性,零部件2是一种采用新材料/技术的非标准件,由于生产制造难度高,其产出率具有随机性。运用随机非线性规划方法,以装配商期望利润最大化为目标,本文建立了零部件订购决策的多维优化模型。通过求解模型最终刻画了零部件的最优订购策略,并基于随机占优概念进行了灵敏性分析。最后,通过数值算例验证了模型结论并进一步探讨零部件供应不同类风险的影响。
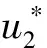
目前关于供应风险下装配系统的最优订购/库存策略研究都只考虑两个零部件的系统,比如,李毅鹏等[15]和Pan与So[16]都考虑随机产出率条件下包含两个零部件的装配系统。可见,多类供应风险下包含n个零部件的装配系统的最优订购/库存策略仍有待学者们深入研究。
