柔性工期下的资源受限项目调度双目标优化研究

刘国山, 林新宇

(中国人民大学 商学院,北京 100872)

0 引言

在资源受限项目调度问题(RCPSP)研究中，项目中各个活动的工期通常是通过类比法、三点估计法、德尔菲估算法等方法提前确定的[1]，且在整个项目执行过程中保持恒定[2]。但是，在实际项目中，通常是每个活动的工作量是确定的，而活动的工期和资源配置是依据资源供给情况、项目截止工期等合理规划产生的[3]。比如说：在新产品研发项目中，由于需要采用新技术、新工艺、或新材料等，项目的创新性较多[4]，此时已有的项目经验不一定适合该项目的工期估计；或者在一些对活动工期没有严格限制的项目中，活动工期设置的灵活性较大，采用上述方法限制了项目调度的灵活性。此时，若活动工期或资源配置结构不科学，则很容易出现资源浪费或者资源不足等极端情况[5]。同时，不合理的活动工期设置，容易使得项目实际执行情况与进度计划偏离较大，进度计划的作用被弱化。在这种背景下，活动工期柔性的特点为提高项目调度计划的科学性和灵活性提供了一种选择。

柔性调度思想在项目调度中的应用主要体现在资源柔性与工期柔性两方面。资源柔性是指资源具备活动实施所需的多种技能[6]，可以以不同的技能形式参与到不同的活动中去，因此资源与活动会存在多种对应关系[7]。同理，柔性思想也可以应用到工期设置上，使工期与活动也存在多种对应关系。多模式下的资源受限项目调度问题(MRCPSP)将活动执行模式扩大到多个，由Talbati首次提出[8]。此后，众多学者对MRCPSP进行了研究[9,10]。但在MRCPSP中，活动的执行模式通常只有两到三种，提供的工期-资源组合种类固定且有限，并不一定能保证包含最优的工期-资源组合，这在一定程度上限制了活动调度的灵活性。因此，本文在MRCPSP的基础上，提出柔性工期项目调度(RCPSP with Variable Duration)模式。将活动工期用区间变量来表示，同时引入 “活动工作量”定义[11]，确定工期与资源的函数关系。这种调度方式扩大了工期-资源的组合范围，项目承包方可以选择最优的工期-资源组合，而不是通过经验进行估计或在较局限的范围内选择。

与此同时，对于新产品研发项目等其他活动工期柔性较大的项目来说，柔性工期的特点为压缩项目总工期提供了一种选择[12]。但是，由于工作量约束的存在，压缩工期的同时，项目对可更新资源的单位日需求量可能会增加，甚至超过日供给量。因此，采用柔性工期项目调度模式，需要考虑项目时间与成本的权衡。关于离散时间-成本权衡的文献，可参考Orm等[13]、张静文等[14]。但以上研究并没有考虑工期的柔性。在柔性工期的背景下，如何基于项目的资源供给情况与截止工期要求，对活动的工期进行合理设置，是项目承包方能否实现项目总工期与成本权衡优化的关键。

综上所述，本文的贡献主要有三方面：第一，本文将柔性调度思想应用于工期设置，为工期的确定提供了依据，提高了项目调度方案的科学性；第二，算例测试结果表明，柔性工期项目调度方法可以有效实现项目完工时间的压缩；第三，本文建立的柔性工期下工期-成本权衡优化模型，可以为项目承包方提供较多可供选择的项目调度方案，可以起到辅助决策的作用，同时提高了项目调度方案选择的灵活性。

1 问题描述与模型建立

1.1 问题描述

在一个项目中，包含n+2个子活动，网络图类型为AON(activity-on-node)。文中涉及的变量及参数的表示和含义如表1所示。项目承包方首先对项目进行WBS分解，然后通过专家估计、小组讨论等方式对项目中各个活动的基准工期进行估计。根据基准模型(见2.2)可计算出项目对可更新资源日供给量，即ak。由于工作量约束的存在，压缩某些活动的工期后，项目对资源的单位日需求会增加，甚至超过日供给量ak。因此，需要考虑时间与成本的权衡。基于上述问题背景，论文建立基准模型与柔性工期模型。

表1 变量及参数的表示和含义

1.2 基准模型

(1)

Sj-Si>di,(i,j)∈E

(2)

(3)

(4)

Sn+1≤D

(5)

xit∈{0,1},i∈Vr

(6)

在已知的活动基准工期下，依据关键路径理论，可以计算出完成整个项目所需的最短工期。在该工期的约束下，可通过基准模型计算出项目对可更新资源的最小日供给量。目标函数(1)为最小化可更新资源的成本；(2)为活动间的逻辑关系约束；(3)为资源约束；(4)为活动的工期表示，且活动不允许中断；(5)为截止工期约束。(6)为决策变量定义域。通过基准模型计算出的项目完工时间及资源供给量作为柔性工期模型的基准线。

1.3 柔性工期模型——模型1

(7)

minf2=Sn+1

(8)

(9)

Sj-Si≥rdi,(i,j)∈E

(10)

rdirrik≥wik,i∈Vr,k∈K

(11)

(12)

(13)

Sn+1≤D

(14)

xit∈{0,1},i∈Vr

(15)

为实现压缩项目完工时间的目的，该模型将活动工期作为决策变量之一，在基准工期的基础上可缩短可延长。该模型为工期-成本双目标优化模型。目标函数(7)为最小化可更新资源的成本，其中第一部分为基准资源供给量以内的资源成本，第二部分为超过基准资源供给量的额外成本；目标函数(8)为最小化项目完工时间；(9)为工期约束；(10)为活动间逻辑关系约束；(11)为工作量约束；(12)为实际资源需求量的表示；(13)为活动实际工期的表示，且活动不允许中断；(14)为截止工期约束；(15)为决策变量定义域。

2 算法描述与算例说明

2.1 算法描述

由于项目调度中的工期-成本权衡是NP-Hard问题[15]，因此本文选择启发式算法对模型1进行求解。模型1的决策变量有两部分，活动工期及开始时间，且活动开始时间的取值范围与活动工期有关。因此，本文在NSGA-Ⅱ算法的基础上，结合随机搜索(Random Searching)算法，提出一种适用于模型1的两阶段嵌套算法，称之为NSGAⅡ-RS算法。算法将活动工期作为主循环中的决策变量，将活动开始时间作为次循环中的决策变量。设主循环(NSGAⅡ)迭代次数为MaxIt1，次循环(RS)迭代次数为MaxIt2，种群规模为nPop，目标维度为nObj。算法的步骤如下：

步骤1种群构造及初始解生成

与NSGAⅡ算法不同，NSGAⅡ-RS算法的种群的迭代分为个体间与个体内两部分循环。首先，每个个体在活动工期范围内随机取值作为工期的初始解。由于每个个体代表的活动工期不同，因此他们代表的活动开始时间的搜索范围也不同，为了减少搜索空间，通过关键路径理论中的正向迭代算法与逆向迭代算法，计算出每个个体对应的活动开始时间区间，即[ES,LS]。然后，引入随机搜索算法，每个个体在[ES,LS]中随机循环取值，作为活动开始时间的初始解。因此，活动工期的初始解个数为nPop，活动开始时间的初始解个数为nPop×MaxIt2，因此，需要通过次循环中的初始解进行筛选。种群的构造见图1。

步骤2算法次循环，计算目标函数值

每个个体在次循环过程中，由于活动工期是不变的，因此依据关键路径理论每次循环得到的项目完工时间是相同的，不同的是在每次循环中活动的开始时间不同，即可更新资源的成本不同。次循环结束后，将成本最低的个体位置作为个体在次循环中的最终位置，通过次循环计算每个个体的目标函数值，并根据约束条件判断其否可行。

步骤3非支配排序

将个体进行两两比较，根据非支配个体的筛选规则，判断每个个体的非支配等级。规则如下：(1)如果两个个体均可行，且个体p1的两个目标函数值均优于个体p2，则个体p1为非支配个体；(2)如果两个个体均不可行，且个体p1的错误值小于个体p2，则个体p1为非支配个体；(3)如果个体p1可行，个体p2不可行，则个体p1为非支配个体；(4)计算每个个体的被支配个数np和该个体支配的解的集合Sp这两个参数；(5)遍历整个种群，将np=0的个体的非支配等级标记为1，并将这些个体从种群中删去，对其余个体重新进行非支配排序，得到非支配等级标记为2的个体；(6)以此类推，直到所有个体都有非支配等级。

步骤4拥挤度计算

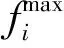
(16)

步骤5交叉、变异、种群合并，以及精英保留策略

采用二进制锦标赛法从种群中选择部分个体，进行交叉、变异，产生新的种群，并将子代种群与父代种群进行合并。对新种群中的个体进行非支配排序(步骤3)与拥挤度计算(步骤4)的操作。由于新种群中个体数目大于设置的种群规模，因此根据精英保留策略对新种群进行筛选，具体规则为：(1)如果个体p1的非支配等级小于个体p2，则p1优于p2；(2)；如果个体p1与p2在同一非支配等级，且个体p1的拥挤度值小于p2，则p1优于p2。根据该策略保留nPop个个体，作为下一次迭代的初始种群。

步骤6输出结果

循环操作步骤2～步骤5，直到达到主循环的最大迭代次数MaxIt1。将非支配等级最高的个体信息输出作为最终结果。

NSGAⅡ-RS算法的流程图见图1。

图1 种群结构

2.2 算例说明

本文通过一个算例对柔性工期模型在缩短完工时间方面的应用进行说明。已知该项目有12个子活动，各个活动间的逻辑关系如图2所示。每个活动基准工期、资源需求以及每种资源的成本信息已知。根据基准模型，可得资源的日供给量，若资源需求超过供给量，则超过部分资源单位成本增加。依据关键路径理论可知项目的最短完工时间为23天，关键路径为0-1-3-6-8-9-11。

图2 算例项目网络图

通过NSGAⅡ-RS算法对基准模型及柔性工期模型进行求解，结果如表2所示。可以发现，柔性工期模型可以对项目完工时间实现有效的压缩，为项目承包方提供了更多选择方案。而且，由于工期的柔性，部分方案(方案4、5、6、7)实现了工期与成本的双重优化。因此可以初步认为，柔性工期是一种有效压缩项目完工时间的策略。

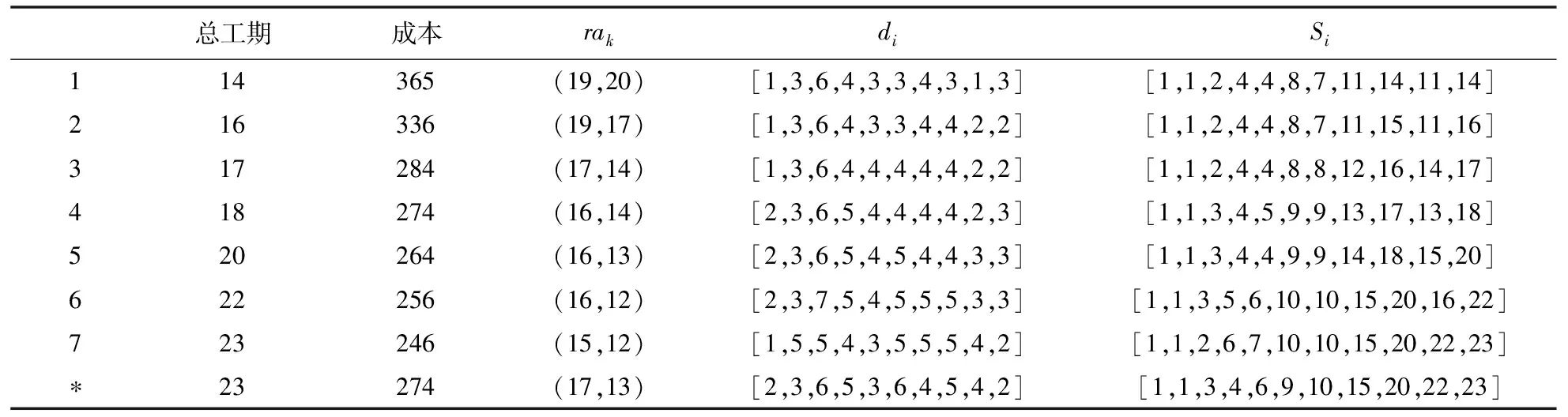
表2 算例柔性工期模型解集

3 计算结果分析

3.1 参数分析

为进一步证明柔性工期模型在压缩项目完工时间上的效果及NSGAⅡ-RS算法的有效性，论文采用PSPLIB数据库1中的480个算例对柔性工期模型及NSGAⅡ-RS算法进行测试。算例中的参数信息如表3所示，测试结果如表4所示。其中，n为项目中实活动个数；k为可更新资源的种类；NC为网络复杂度，反映了网络中每个节点的平均箭头数；RF为资源因子，反映了活动的资源需求，RF越大表示活动需要的资源种类越多；RS为资源强度系数，反映了资源的供给强度，RS越大表示资源的供给越多；FF为工期柔性因子，反映了活动工期的柔性程度，FF越大表示活动工期的取值区间越大。(表中数据均为以FF=0作为基准计算得出，且分别展示了项目完工时间的最大优化比例(Max-makespan%)与平均优化比例(Mean-makespan%)以及项目成本的最大增加比例(Max-cost%)以及平均增加比例(Mean-cost%)。)

表3 算例参数信息

表4 算例测试结果-柔性工期模型

由表4可知，柔性工期策略可以较好的实现项目完工时间压缩，且压缩比例受到柔性系数的影响，柔性系数越大，项目完工时间可压缩比例越大。由图3可知，柔性系数的边际效用是递减的。但是，由于工期与成本的反比关系，实现工期压缩的同时，项目成本也会增加，增加的比例会因资源成本的改变而改变。同时，因提前完工带来的奖励会抵消部分增加的成本。此外，项目完工时间的压缩水平和NC、RF、RS没有明显关系，浮动水平不大，因此，柔性工期策略是一种鲁棒性较好的项目完工时间压缩策略。

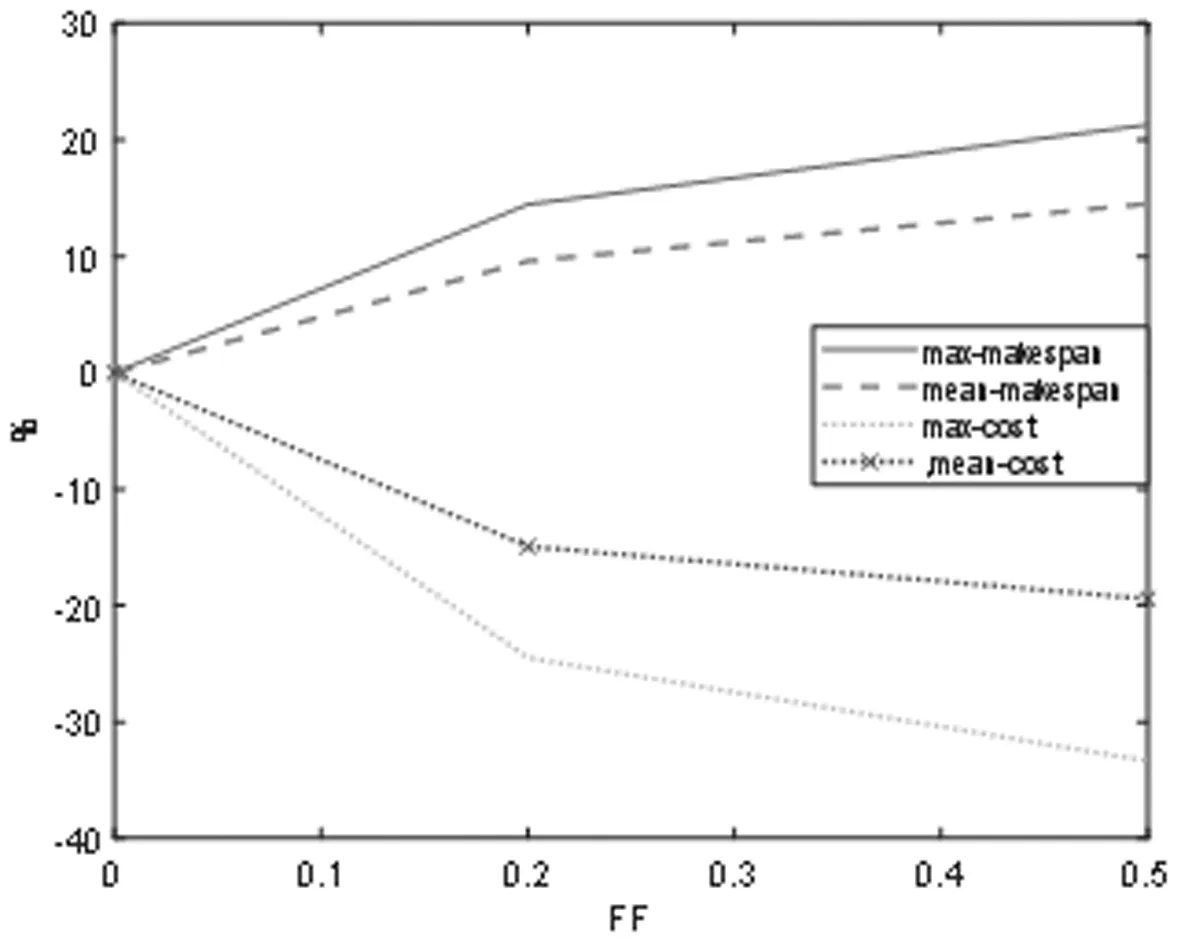
图3 算例测试结果图—FF

3.2 不同压缩完工时间策略对比分析

活动重叠策略为文献中通常使用的压缩完工时间的策略之一，即放松活动间逻辑关系约束。比如武汉火神山医院的建设，采用了边设计边施工的建设方式，大大减少了工程所需的完工时间。但在活动重叠策略下，由于紧前活动信息的不完全性，紧后活动会出现部分返工的情况，导致项目工期或成本的增加。两种压缩完工时间策略对比见附表3。

本文基于文献Chu等[12]对活动重叠策略进行建模(详见附录)。该文献基于设计结构矩阵(DSM)引入了PO和RI两个矩阵，分别代表紧前活动对其紧后活动的重叠时长影响因子和返工影响因子。举例来说，PO(i,j)=0.7意味着活动j最早可在活动i完成70%后开始；RI(i,j)=0.2意味着如果两个活动的重叠时长为Δij，则j的返工时长为0.2Δij。活动的实际工期为基准工期加返工时长。设二进制决策变量hi为某活动是否与其紧前活动重叠。

为将两种策略在压缩项目完工时间上的表现能力进行对比，本文利用Progen随机产生一个算例，分别用以上三个模型进行求解，并对FF、PO、RI等进行参数分析。算例信息见表2。算例测试结果见表5。

表5 算例测试结果——两种压缩完工时间策略对比

由表5可知，两种压缩完工时间策略都大致呈现出工期与成本的反比关系，且随着FF或RI的增加，压缩完工时间的能力增加，变化趋势基本一致，两种策略能实现的最大工期压缩程度相差不多。在同一算例下，更换压缩工期策略，可以取得与已有研究类似的结果，进一步证明了本文提出的模型及算法的科学性与有效性。然而，对不同的项目来说，由于不同项目的各种参数不同，比如柔性因子、返工因子、提前完工奖励因子、资源边际成本、截止工期等，不同策略的工期和成本表现能力都会受到一定的影响。当项目对活动间的逻辑关系要求较高时，同时活动的工期没有严格限制时，可以采用柔性工期策略实现项目完工时间的压缩；当项目对活动间的逻辑关系要求较低，同时活动的工期受到严格限制时，可以采用活动重叠策略实现项目完工时间的压缩；当项目对活动间的逻辑关系要求较低，同时活动的工期没有严格限制时，两种策略均可，但考虑到返工对项目成本、员工效率及企业声誉等带来的负面影响，柔性工期策略较优。在实际应用中，项目承包方可以依据不同项目的特点，通过计算分析，合理选择最适合本项目的策略，实现工期与成本的双重优化。

4 结论

在资源受限项目调度问题(RCPSP)研究中，各个活动的工期往往都是已知且固定的。工期设置的是否合理也会影响到整个项目调度安排的合理性，包括完工时间以及资源配置。因此，本文在已有研究的基础上，将柔性调度思想应用于项目中各个活动的工期设置。与MRCPSP不同，柔性工期调度方式提供的工期-资源组合范围更广，可以依据项目截止工期、资源供给情况等从中选出最优的工期-资源组合。为验证柔性工期调度方式对项目工期和成本的影响，论文建立了工期-成本双目标权衡优化模型，并将其与工期已知下的基准模型进行对比，证明柔性工期调度方式在压缩项目完工时间方面的作用。而且，论文设计了一种两阶段的嵌套算法，NSGAⅡ-RS算法。实验证明，该调度方式是一种鲁棒性较好的压缩完工时间的策略，且工期的柔性系数越大，对压缩完工时间起到的作用越大，但边际效用是递减的。同时，本文将柔性工期调度策略与活动重叠策略进行对比，两种策略特点不同，在实际项目应用中，项目承包方应根据项目具体情况合理选择项目调度方案。在未来的研究中，可以进一步考虑资源供给的不确定性对活动工期和开始时间的选择以及项目的完工时间和成本带来的影响。