疏浚工程施工耙吸船装舱效率分析

张志勇，严 娟

(长江水利委员会河湖保护与建设运行安全中心，湖北 武汉 430010)

自航耙吸挖泥船(TSHD)是一种主要的疏浚施工船，具有良好的航海性能，自航、自挖自卸，不需要占用大量水域或封锁航道，世界各国疏浚河港广泛使用。在疏浚工程施工作业时，TSHD下放耙臂，通过耙头疏松泥沙，再由泥泵将松动的泥沙经管路吸入泥舱完成疏浚。施工中，一般会采用边装舱边溢流的工艺，以增加装载量。这个过程中，部分细颗粒会随溢流流出泥舱，这被称为溢流损失。以合理的时间进行装舱溢流施工，使装舱量最大化、溢流损失最小化，对耙吸疏浚而言是极其重要的。不同粒径泥沙在装舱过程中的沉积、冲刷等特性是不同的，并且会显著影响装舱溢流施工过程，这就需要开展针对性研究，掌握泥沙在装舱过程中的运动特性，并据此确定合理的装舱溢流时间等关键施工参数，进而提高实际施工的装舱效率。

目前已开展的相关研究有：Vlasblom和Miedema基于Camp模型的泥舱沉积理论研究；Ooijens在Camp模型中加入了动力学计算，并通过大比尺模型实验测量了装舱过程中的流速和浓度等；Cees van Rhee提出了装舱过程的简二维CFD计算模型。在这些研究中心，有些基于沉降理论估算溢流损失，有些是计算流体力学方法对装舱溢流的流态过程进行模拟，从而得到模拟计算的产量，Camp模型沉积理论的方法简单快捷，但不能反映出泥舱结构对溢流的影响；Van Rhee 的模型虽然模拟了装舱的过程(包括溢流)，但是受制于二位模型的局限性，只能反映泥舱的基本结构，并且仅对单一粒径进行了分析，而不能对多粒径组泥沙的沉积特点及相互的影响进行分析。

本文针对泥沙在装舱溢流过程中的特性差异及对施工参数的影响，根据郝宇驰等由RANS方程与泥沙经验公式相结合所建立的装舱溢流数值计算方法，分别基于长江口航道疏浚工程和长江下游12.5 m深航道疏浚工程施工现场实测数据，建立15 800 m3和11 800 m3耙吸挖泥船泥舱模型，具体模拟了细沙和粗沙的装舱溢流全过程，对装载量进行了实测数据验证，并估算了溢流损失量，据此给出合理装舱溢流时间等关键施工参数的确定依据。

1 模型基本方程

1.1 流体力学方程

基于流体不可压缩的假定，连续性方程及动量方程分别为

(1)

(2)

式中：VF为流动的体积分数；ρ为流体密度；RDIF为流体湍流扩散项；RSOR为流体质量源项，流体的速度分量(U,V,W)分别是对应(x,y,z)坐标系或(r，θ，z)坐标系的对应方向值；Ax，Ay，Az分别为3个方向自由面流动的面积分数；Gi为加速度。

1.2 泥沙运动方程

耙吸装舱过程，包括泥沙的悬浮和沉积、冲刷、推移等运动过程。

1)悬浮沉积。泥沙的输运连续性方程为：

(3)

其中：cs,j为悬浮泥沙的浓度；u是水沙混合物的平均流速。

2)冲刷过程。Shields对各种泥沙颗粒进行了临界起动试验，实测得到无量纲临界起动剪切应力与颗粒雷诺数的Shields关系曲线。随着沉积面的升高，泥舱过流面积缩小，流速增大，达到临界流速时，沉积泥沙再次起动，由于起动冲刷问题的复杂性，只能采用经验公式来计算此过程。根据资料，选用基于Mastbergen和Von den Berg[1]的经验公式：

(4)

(5)

床面的Shields数θj则根据剪切应力τ计算：

(6)

3)推移过程。推移是较大颗粒泥沙沿沉积面滚动或跳动形成的泥沙运动形式。选用Meyer，Peter和Muller的公式计算：

Φj=βj(θj-θcr,j)1.5

(7)

式中，Φj是无量纲推移质输送率，与单宽体积推移质输送率qj的关系为

(8)

2 边界条件

2.1 壁面边界条件

泥舱壁面定义为无滑移壁面边界，在对称边界上流量通量为0，流体剪切应力为0，即在与壁面边界相邻的水体周围，固壁结构是固定的；水体可以沿边界自由滑动，但不能穿透也不能拉开固壁边界。

2.2 溢流边界条件

为模拟溢流过程，设定了自由出流边界条件，该条件实质上是Sommerfeld辐射边界条件，即在边界上：

(9)

式中：φ为所要辐射的变量；C为波浪传播的速度；n为辐射边界的法向向量。

3 不同粒径的装舱特性分析

为了分析粒径差异对装舱过程的影响，设置与Miedema和Van Rhee相同的参数，泥舱舱容约15 800 m3。模拟选用的装舱泥沙中值粒径d50为0.4 mm的欧洲北海中沙。表1是模拟工况，计算时间为7 000 s。

表1 装舱过程参数

各粒径组在装舱溢流的过程中溢流损失变化见图1。

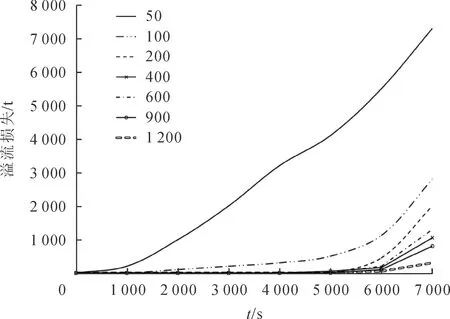
图1 各粒径组的溢流损失随时间的变化

根据图1可知，从实际来说，细颗粒泥沙溢流损失发生时间早于粗颗粒；从损失量来说，细颗粒泥沙也明显大于粗颗粒。50 μm粒径泥沙的溢流损失约占损失总量的50%，100 μm约占12%，200 μm约占18%，400 μm约占8%，600 μm约占6%，900 μm约占4%，1 200 μm约占2%。50 μm颗粒是溢流损失的主要部分，其溢流损失率(曲线斜率)随着装舱时间的增大而增大，其余粒径组在5 600 s时刻前损失率较小，之后明显开始增大。可以看出，各种不同粒径的疏浚土在泥舱中的沉积、冲刷特性是显著不同的，需要针对性的制定工艺，提高施工效率。

4 实船装舱过程分析

4.1 细沙装舱过程模拟

根据船舶结构图，建立15 800耙吸挖泥船三维泥舱数学模型，根据长江口航道疏浚工程现场实测数据对装载量和土方量的计算进行验证，并开展装舱溢流损失分析。实船现场数据测试，施工参数见表2。

表2 盐城大丰港典型装舱过程参数

将现场实测装载量与土方量(最终留在舱内的泥沙换算为自然状态下的重量)和模型计算结果进行对比，绘制装载量曲线与土方量时间变化曲线，见图2。计算结果与实测数据基本一致。

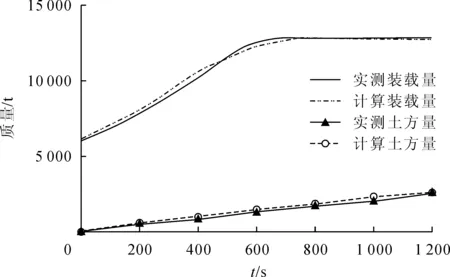
图2 15 800 m3装舱过程对比验证

由于该工程疏浚泥沙颗粒较细，因此，在该段时间内，通过装舱最终沉积在舱底的泥沙较少，泥舱中大部分泥沙处于悬浮状态。由于该工程实际施工中，挖泥船单次装舱时间约1 h，因此将装舱溢流过程的模拟时间扩展到3 600 s，得到以下结果，见图3。

根据计算结果，在330 s时开始溢流，溢流泥沙含量随时间逐步增大，约700 s时溢流泥沙含量的增长率明显加大(对应于溢流泥沙含量曲线的斜率变大)；1 000 s时达到145 kg/m3，之后增幅变缓，2 700 s左右时溢流泥沙含量达到270 kg/m3，逐渐接近装舱浓度(装舱入流泥沙含量约300 kg/m3)。由图3可知，溢流损失率可分为低中高三个阶段。2 700～3 000 s以后，总装载量的增长比较有限，而溢流损失增幅明显，说明此后的装舱过程效率较低。建议装舱时间为2 700 s，由于在具体施工过程中，还受到潮流、波浪、疏浚进度、抛泥区位置、环境要求等因素的影响，因此，建议在确定装舱时间时，综合各因素确定。

图3 装舱溢流过程中的溢流浓度与溢流损失对比

4.2 粗沙装舱过程模拟

长江下游12.5 m深水航道疏浚工程，疏浚泥沙中值粒径d50为0.76 mm，施工船舶为舱容11 800 m3的自航耙吸挖泥船，根据施工记录，航行运距约46 km，装舱时间约1.8 h。实处船测试数据作为模拟工况，模型计算时间为6 200 s。计算起始水深约3.0 m。

进口采取现场实测的时间序列浓度值和入流流量值，11 800 m3的自航耙吸挖泥船泥舱分为4个入流口装舱。装舱模拟的相关参数见表3。工程现场主要为粗沙，因此泥沙在进入泥舱后迅速沉积，图4是15 800 m3的自航耙吸挖泥船泥舱内的泥沙沉积情况模拟结果。可以看出，在1 500 s时，泥舱底部已经沉积了大量的泥沙。

表3 装舱模拟的相关参数

图4 15 800 m3的自航耙吸挖泥船装载过程对比验证

将现场实测的装载量与土方量(最终留在舱内的土方量)和模型计算结果进行对比，并绘制装舱量曲线、土方量曲线和溢流损失曲线。通过对比可见，装舱量和土方量的模拟结果与实测数据是基本一致的，说明所建立15 800 m3的自航耙吸挖泥船泥舱粗沙装舱的三维数学模型是准确可信的。

通过对装载曲线和溢流损失曲线的分析可知，由于粗沙颗粒粗、较易沉积。因此，在整个装舱过程中，大部分泥沙都留在舱内，并且沉积量较多。根据溢流损失曲线，溢流开始时间为2 460 s，其后，溢流泥沙损失比(每时刻溢流泥沙量相比于入流泥沙量的比值)迅速由0增加至4.5%左右(2 460～4 000 s区间)，后续溢流增量趋于平缓(4 000～5 500 s区间)，在5 500 s以后溢流损失量的增幅再次增大。

4.3 粗沙和细沙装舱特性对比分析

将细沙和粗沙的装载量、溢流损失量都除以各自的总量，转化为相对值，得到图5。由图5中曲线对比分析，长江口航道疏浚工程为细沙，装舱历时较短，长江下游12.5 m深水航道疏浚工程为粗沙，装舱浓度较小，装舱历时较长，由于粗沙较易沉积，因此，大部分都留在舱内。从装载量曲线来看，细沙和粗沙开始溢流的时刻都处于总时间的20%左右，之后装载曲线斜率均开始变缓，但是粗沙的装载曲线斜率明显大于细沙，细沙在装载总时间的60%时，装舱曲线近乎水平，说明细沙的溢流损失占比较大，在该时刻以后的装舱效率较低；粗沙在装舱总时间的85%之前，还可以保持较高的装舱效率。从溢流损失来看，细沙比粗沙溢流损失发生的快、溢流损失总量多。细沙的溢流损失基本和溢流同步开始，而粗沙的溢流损失则相对滞后于溢流开始时刻，这是因为细沙在装舱过程中处于悬浮状态的多一些，粗沙则相对在底层分布的多一些。

图5 细沙粗沙装舱溢流特性对比

5 结 语

1)利用Miedema和Van Rhee的典型模型，分析了不同颗粒泥沙的装舱特性，根据分析结果，从时间来说，细颗粒泥沙溢流损失发生时间早于粗颗粒；从损失量来说，细颗粒泥沙也明显大于粗颗粒。

2)针对长江口航道疏浚工程和长江下游12.5 m深水航道疏浚工程实测数据，分别模拟分析了细沙和粗沙的装舱溢流过程，并据此确定了合理装舱溢流时间等关键参数。

3)细沙通过装舱最终沉积在舱底的泥沙较少，泥舱中大部分泥沙处于悬浮状态，舱过程可分为低中高溢流损失率三个阶段，进入高溢流损失阶段以后，总装载量的增长比较有限，溢流损失增幅明显，装舱效率较低，合理装舱时间应该选在高溢流损失阶段。

4)粗沙在进入泥舱后迅速沉积，溢流开始后，溢流泥沙损失比迅速增加至4.0%左右，后续溢流增量趋于平缓，在5 500 s以后溢流占比的增幅再次增大，由于粗沙可以一直保持一定的净装舱率，合理的装舱溢流时间应该结合水环境、抛沙距离等因素的影响，尽可能延长。

5)细沙粗沙开始溢流的时刻大致都处于总时间的20%左右，之后装载曲线斜率都变缓，但是粗沙的装载曲线斜率明显大于细沙，细沙在装载总时间的60%时，装舱曲线近乎水平，说明细沙的溢流损失占比较大，在该时刻以后的装舱效率较低；粗沙在装舱总时间的85%之前，还可以保持一定的装舱效率。从溢流损失来看，细沙比粗沙溢流损失发生的快、溢流损失总量多。细沙的溢流损失基本和溢流同步开始，而粗沙的溢流损失则相对滞后于溢流开始时刻，这是因为细沙在装舱过程中处于悬浮状态的多一些，粗沙则相对在底层分布的多一些。