通信时延下UAV/UGV混合编队控制系统的稳定性分析

朱 旭，赵文杰

(长安大学 电子与控制工程学院，西安 710064)

0 引言

无人机(UAV，unmanned aerial vehicle)/无人车(UGV，unmanned ground vehicle)混合编队控制，通过空地协作，可以实现UAV编队和UGV编队在感知、通讯、负载等方面的互补，提高整个系统的灵活性和对未知环境的适应性，从而完成单独UAV编队或UGV编队难以完成的任务，如空地立体化交通监管、快速精准跟踪追逃、协同定位、紧急救援等[1-2]。

然而，UAV与UGV之间存在巨大差异，不同的工作空间、不同的动力学特性，使得UAV/UGV混合编队控制变得异常困难[3-4]。同时，由于网络通讯环境和通讯带宽的限制，混合编队的交互信息中含有通信时滞，导致控制系统的稳定裕度急剧下降，甚至引发系统不稳定，进一步加剧了混合编队控制的难度[5-7]。因此，研究通信时延下UAV/UGV混合编队控制系统的稳定性具有重要意义。

关于通信时延下控制系统稳定性的研究，有两大类方法：时域方法、频域方法[8]。时域方法是当前的主流方法，往往基于Lyapunov-Razumikhin定理或Lyapunov-Krasovskii泛函进行研究[9-12]。然而，时域方法仅能获取通信时延下控制系统稳定的充分条件，而非充要条件，具有很大的保守性[13]。

频域方法致力于研究通信时延下控制系统特征方程的求解问题，可以获取系统稳定的充要条件[14]。但是，时延系统的特征函数具有无穷多个特征根，现有的数学工具无法计算出其所有特征根，所以更关注临界虚根(位于复平面虚轴上的特征根)求解[15]。常用的临界虚根求解方法有：Rekasius代换法[16]、辅助特征函数法[17]、直接法[18]、τ分解法等[19]。这些临界虚根求解方法各有优缺点，这里推荐辅助特征函数法，其主要优势包括：(1) 对临界虚根的检测可简单有效地通过求解辅助特征方程完成；(2)在辅助特征方程没有重根的前提下，所有临界虚根的稳定性行为可以直接判断，无需其他计算[20]。

目前，利用频域方法分析通信时延下UAV/UGV混合编队控制系统稳定性的研究较为匮乏，存在一些关键难题。比如，囿于UAV/UGV的异构特性，难以将频域方法直接应用于混合编队的复杂系统特征方程的求解。特别地，随着UAV、UGV数量的增加，混合编队系统特征方程的维数不断增加，临界虚根求解运算量呈指数膨胀，导致“维度爆炸”问题。因此，研究通信时延下UAV/UGV混合编队控制系统的稳定性问题，推导系统稳定的充要条件，尚存在研究瓶颈。

综合以上分析，本文研究通信时延下UAV/UGV混合编队控制系统的稳定性分析问题，旨在推导系统稳定的充要条件，计算准确的时延边界，即可容许的最大时延。首先，建立考虑UAV/UGV异构特性的混合编队模型，并描述混合编队的通信关系。接着，针对UAV群组、UGV群组，分别设计基于信息一致性的分布式控制器，并构建UAV/UGV混合编队控制系统。然后，利用矩阵相似变换，将高维异构的UAV/UGV混合编队控制系统降维拆分为若干等价的低维子系统，降低解析难度和运算量。最后，采用辅助特征函数法计算这些子系统特征方程的临界虚根，获取系统稳定的充要条件，得到准确的时延边界，并通过仿真验证了所提理论方法的有效性。

1 UAV/UGV混合编队建模

首先，对UAV、UGV分别进行建模，并确立UAV/UGV的共同控制量；然后，构建UAV/UGV混合编队的通信拓扑，描述编队的通信关系。

1.1 UAV与UGV建模

在地面惯性坐标系OXYZ中[21]，由于无人车仅在OXY平面运动，因此选取平面运动状态作为UAV/UGV共同的控制量，而高度协同控制只在UAV群组内部进行。UAV模型选用四旋翼，UGV模型选用双轮差分驱动式。

首先，四旋翼无人机的运动学模型为[22]：

(1)

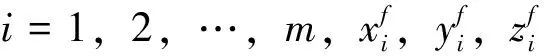
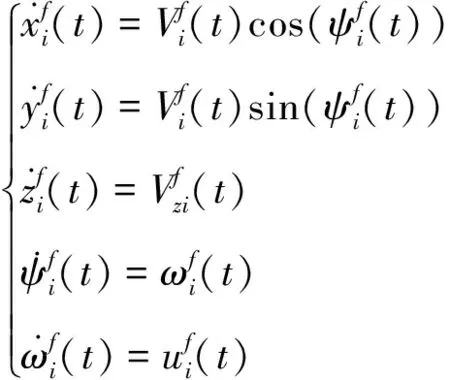
(2)

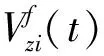
再者，双轮差分驱动轮式移动机器人的运动学模型为[23]：

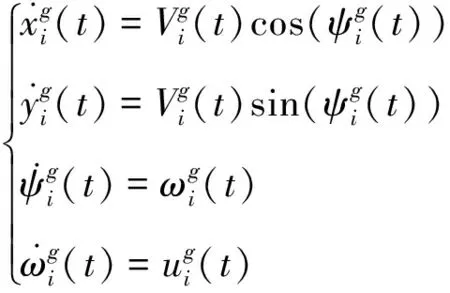
(3)

为了实现UAV/UGV混合编队在平面的协同，选取偏航角和偏航角速度作为UAV/UGV共同的控制量。

1.2 UAV/UGV混合编队的通信拓扑

考虑由m架四旋翼UAV、n-m辆双轮差分驱动UGV所构成的混合编队，其通信拓扑可以用图论的相关知识进行描述[24-25]。

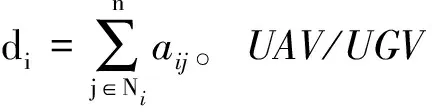
UAV/UGV混合编队可以分为UAV群组和UGV群组，Γ1={1,2,…,m}，Γ2={m+1,m+2,…,n}分别表示UAV、UGV的集合，有Γ1∪Γ2=v。Lf∈m×m是UAV群组通信拓扑的拉普拉斯矩阵，Lg∈(n-m)×(n-m)是UGV群组通信拓扑的拉普拉斯矩阵。

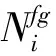
2 通信时延下UAV/UGV混合编队的稳定性分析

针对通信时延下的UAV/UGV混合编队，设计分布式控制器，并分析编队的稳定性，获取准确的时延边界。首先，设计通信时延下基于一致性算法的UAV/UGV混合编队分布式控制器，并推导编队的闭环系统特征方程。然后，根据UAV/UGV编队的闭环系统特征方程，推导编队稳定的一组必要条件；继而利用辅助特征函数法对带有通信时延的UAV/UGV混合编队进行稳定性分析，证明只有一个时延区间可以令编队稳定，并得到编队稳定的充要条件，获取准确的时延边界。

2.1 UAV/UGV混合编队的分布式控制器设计

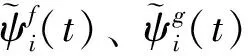
(4)

其中:ψd(t)、ωd(t)为UAV/UGV混合编队的期望偏航角和期望偏航角速度。UAV/UGV混合编队的控制目标为：

(5)

接下来，针对UAV群组、UGV群组，分别设计基于信息一致性的分布式控制器：

(6)

(7)

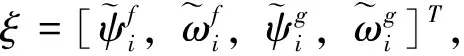
(8)

其中:

其中:I为单位矩阵。定义矩阵L*为：

(9)

存在变换矩阵U，使得通过相似变换U-1L*U=Λ，得到对角矩阵Λ，Λ的特征值与L*相同，设这些特征值为γ1,γ2,…,γn。利用上述相似变换，推导出UAV/UGV混合编队控制系统的特征方程：

f(λ,τ)=|H1+H2e-λτ-λI|=

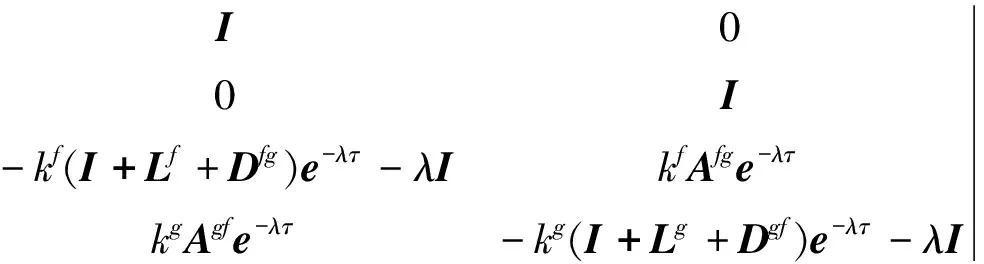
|U-1(λ2I+(λ+1)e-λτL*)U|=

|λ2I+(λ+1)e-λτΛ|=

(10)

其中:λ为拉氏变量，fi(λ)为对控制系统特征方程进行降维拆分后的子系统特征方程，其形式为：

fi(λ,τ)=λ2+γi(λ+1)e-λτ

(11)

至此，利用矩阵相似变换，将高维异构的混合编队控制系统(8)降维拆分为若干等价的低维子系统(11)，分析这些子系统的稳定性与分析原UAV/UGV混合编队控制系统等价，可大幅度降低稳定性分析的解析难度和运算量。

2.2 准确时延边界求解

针对通信时延下UAV/UGV混合编队控制系统的稳定性分析分为两部分。首先，给出整个系统稳定的一组必要条件，推导无时延情况下的稳定性判据。然后，利用辅助特征函数法，证明只存在一个时延区间可以令编队稳定，并计算通信时延下系统准确的时延边界，得到编队稳定的充要条件。

无时延情况下UAV/UGV混合编队控制系统的稳定条件，是有时延情况下系统稳定的前提和必要条件。因此，先给出无时延情况下的稳定性判据。

引理1：对于τ=0，当且仅当γi>0时，i∈V，UAV/UGV混合编队控制系统(8)是Hurwitz稳定的。

证明：由于分析UAV/UGV混合编队控制系统(8)的稳定性与分析各个子系统(11)的稳定性等价，所以计算τ=0时子系统(11)的特征方程：

fi(λ,0)=λ2+γiλ+γi

(12)

用劳斯判据推导式(12)Hurwitz稳定的充要条件，即γi>0。

接下来，给出通信时延下UAV/UGV混合编队控制系统的稳定性判据。

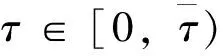
(13)

证明：子系统(11)的特征方程可以写为如下形式：

fi(λ)=a0(λ)+a1(λ)e-λτ

(14)

其中:a0(λ)=λ2，a1(λ)=γi(λ+1)。

定义辅助特征函数Fi(Wi)：

Fi(Wi)=Re(a0(iαi))2+lm(a0(iαi))2-

Re(a1(iαi))2-lm(a1(iαi))2

(15)

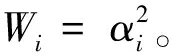
(16)

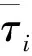
(17)

解方程组得到式(11)的时延边界为(13)。

3 仿真结果与分析

为了验证所提出通信时延下UAV/UGV混合编队稳定性分析方法的有效性，使用由3架UAV和3辆UGV构成的混合编队进行仿真。混合编队的通信拓扑如图1所示。

图1 UAV/UGV混合编队的通信拓扑

图1所示通信拓扑对应的L*为：

L*的特征值为γ1=13.392 3，γ2=9.464 1，γ3=5.531 9，γ4=1.280 3，γ5=2.535 9，γ6=3.795 6。所有的特征值均大于零，满足引理1。

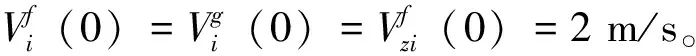
接下来，分三种情况验证定理1的正确性。三种情况的时延大小有差异，分别为：1) 时延略小于边界值，τ=0.110 0 s；2) 时延等于边界值，τ=0.111 4 s；3)时延略大于边界值，τ=0.112 0 s。

情况1：τ=0.110 0 s

UAV/UGV混合编队的偏航角和偏航角速度变化曲线分别如图2、图3所示，偏航角误差和偏航角速度误差曲线分别如图4、图5所示。UAV/UGV的偏航角在50 s之内趋近于控制目标80°并保持不变，偏航角速度趋近于0，偏航角误差、偏航角速度误差也均在50 s内趋近于0。由此可知当通信时延τ=0.110 0 s时，UAV/UGV混合编队控制系统是稳定的。

图2 τ=0.110 0 s时的偏航角

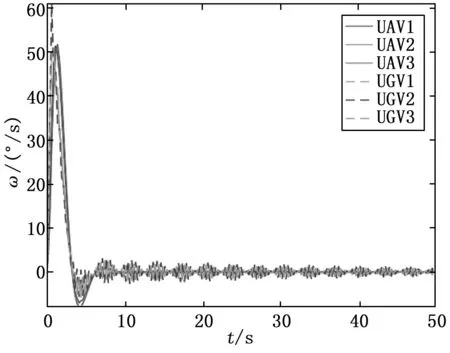
图3 τ=0.110 0 s时的偏航角速度

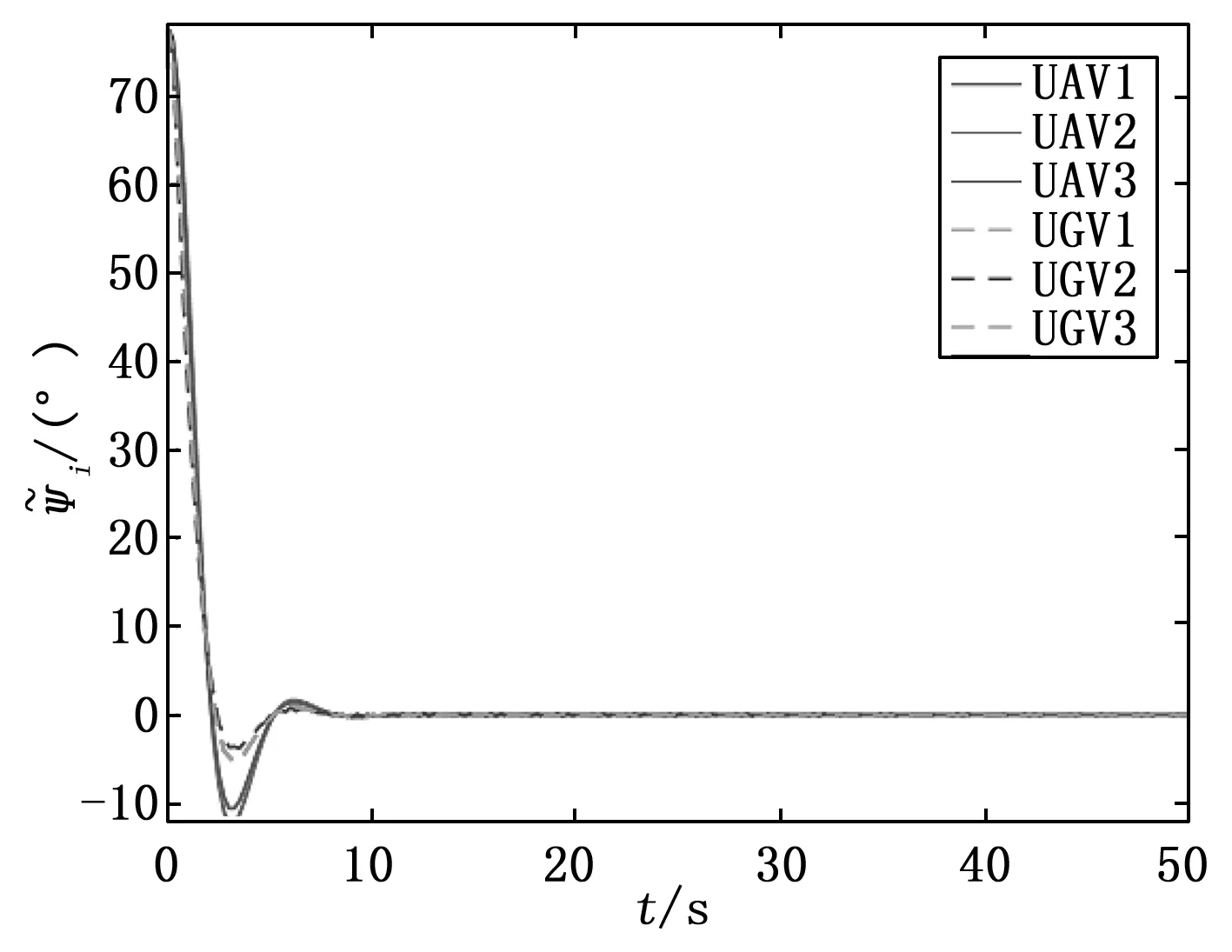
图4 τ=0.110 0 s时的偏航角误差

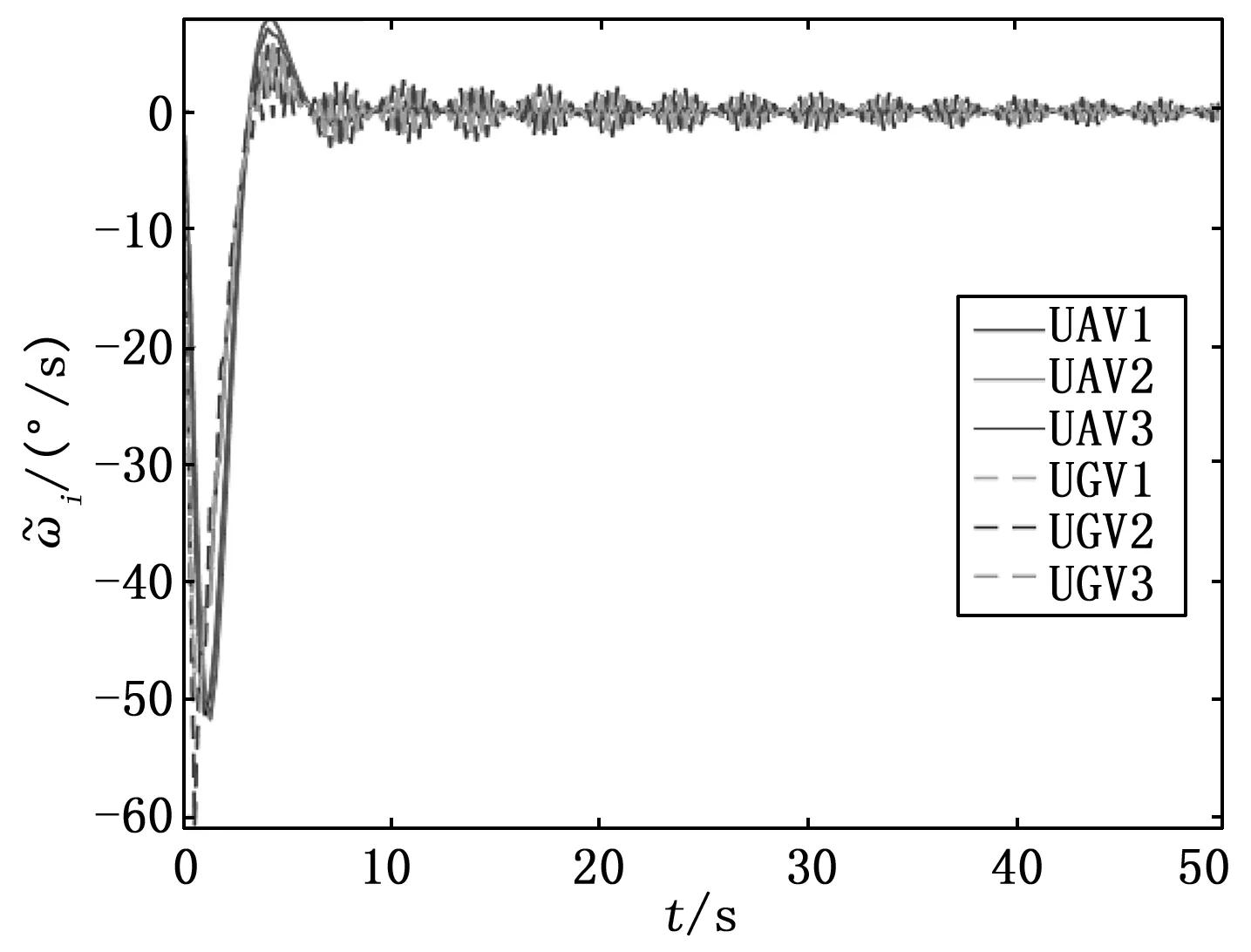
图5 τ=0.110 0 s时的偏航角速度误差

UAV/UGV混合编队的OXY平面运动轨迹如图6所示，三维运动轨迹如图7所示。UAV/UGV混合编队系统在50 s内达到稳定状态。

图6 UAV/UGV混合编队的OXY平面运动轨迹

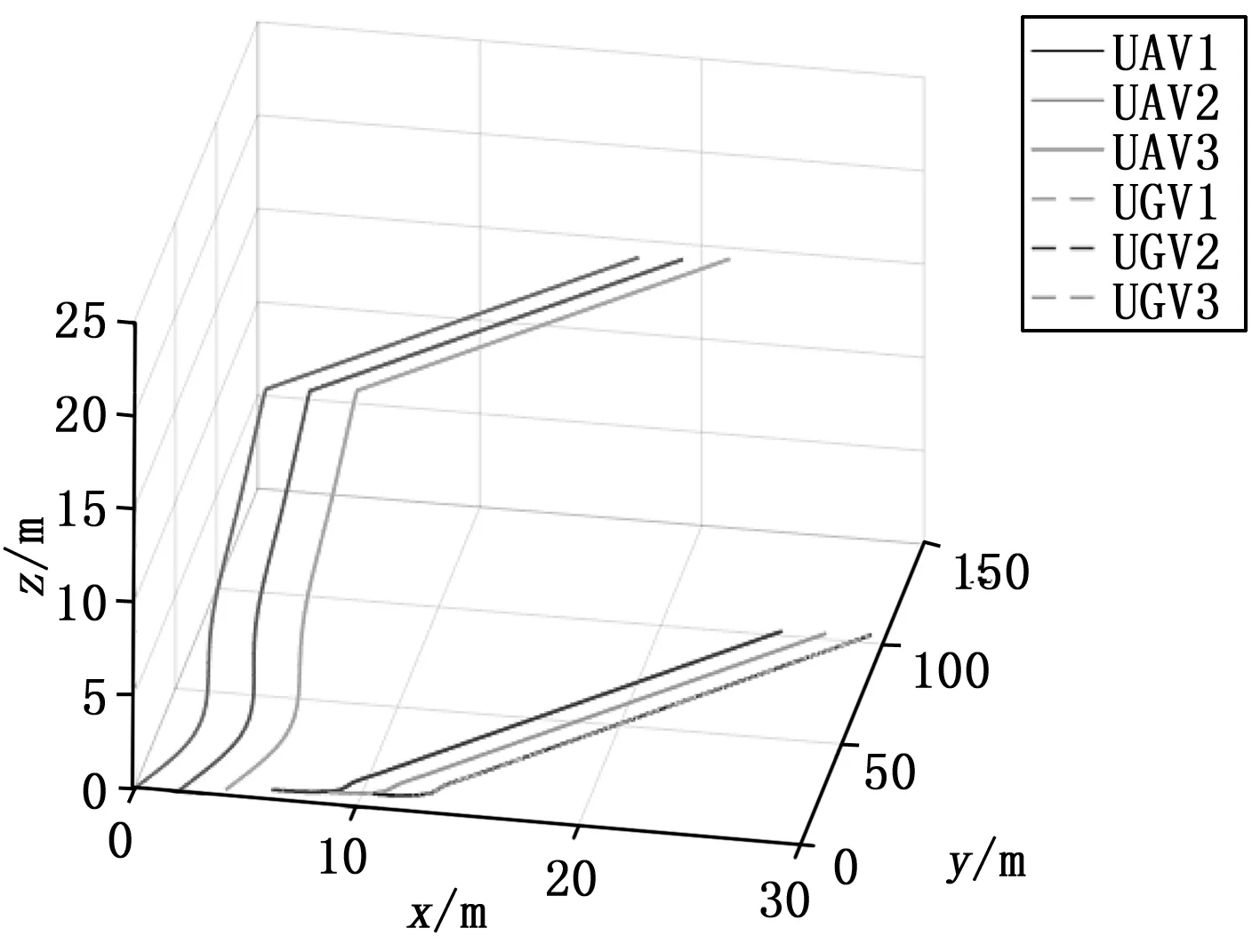
图7 UAV/UGV混合编队的三维运动轨迹

情况2：τ=0.111 4 s

UAV/UGV混合编队的偏航角误差和偏航角速度误差分别如图8、图9所示。此时，系统的状态呈现等幅振荡，UAV/UGV混合编队控制系统临界稳定。

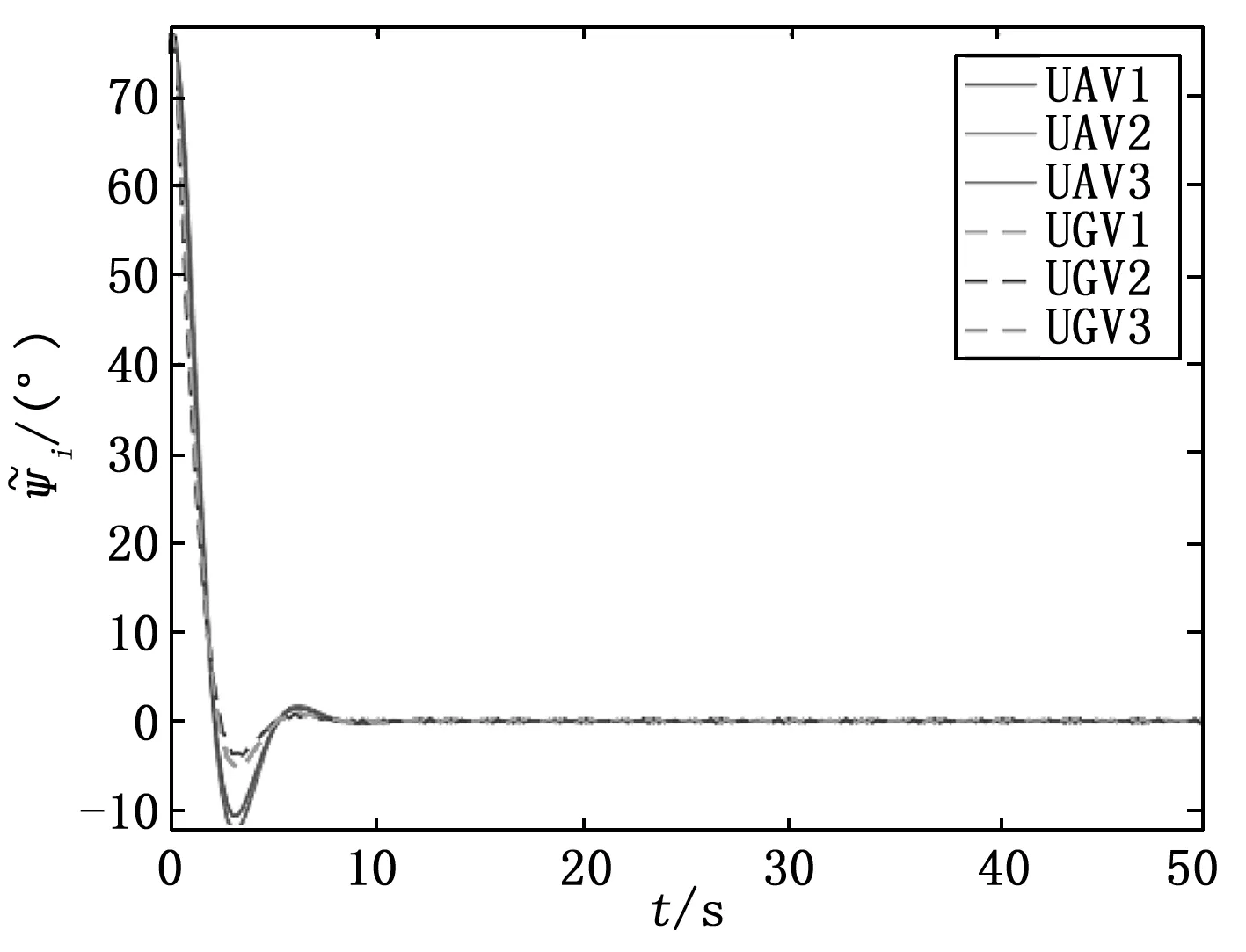
图8 τ=0.111 4 s时的偏航角误差

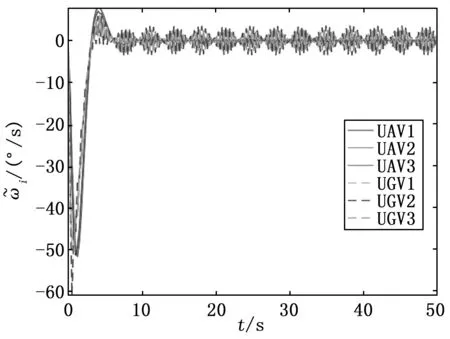
图9 τ=0.111 4 s时的偏航角速度误差

情况3：τ=0.112 0 s

UAV/UGV混合编队的偏航角误差和偏航角速度误差分别如图10、图11所示。此时，混合编队的偏航角误差、偏航角速度误差曲线均发散，UAV/UGV混合编队控制系统不稳定。

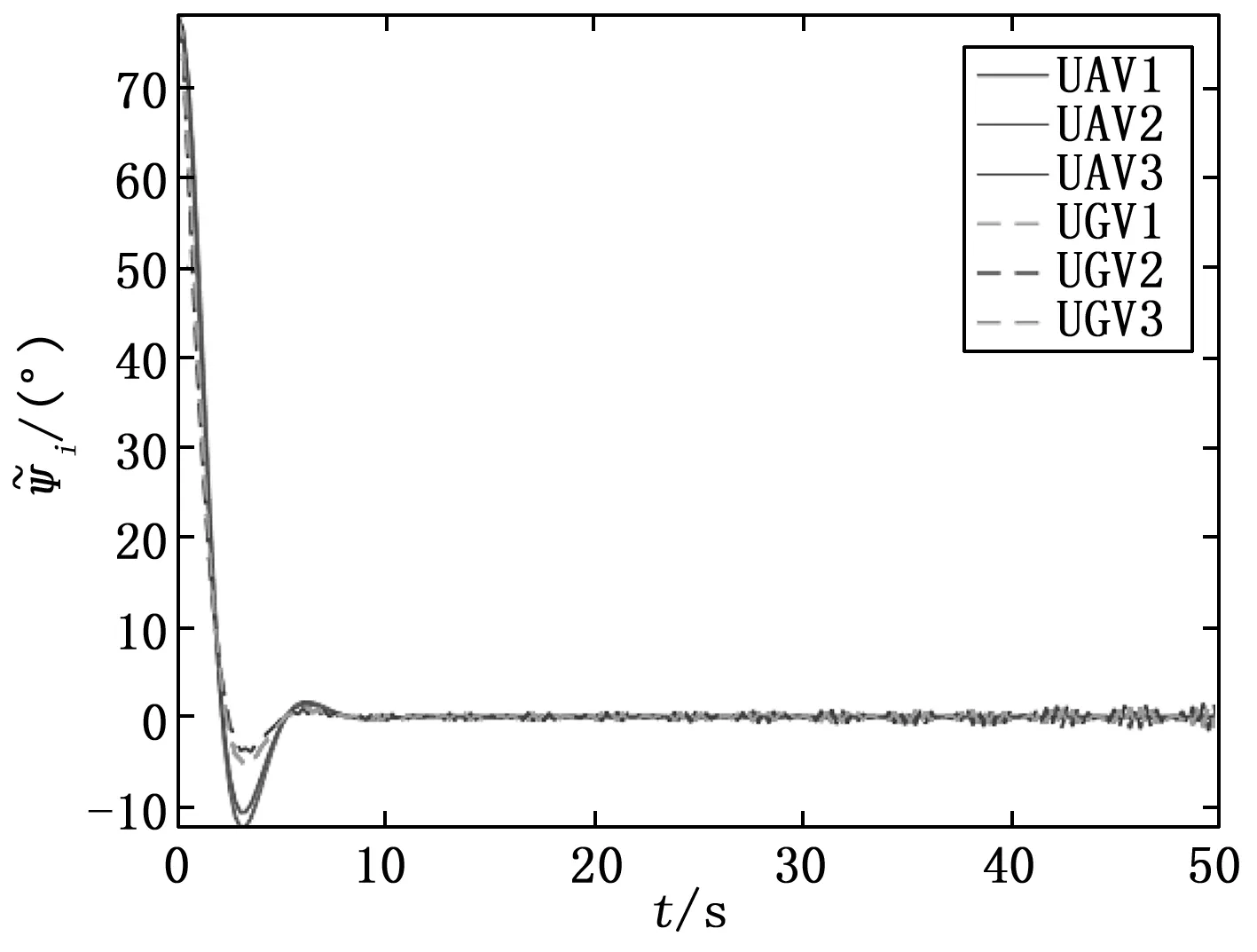
图10 τ=0.112 0 s时的偏航角误差

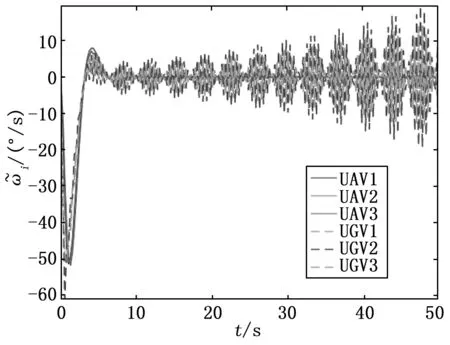
图11 τ=0.112 0 s时的偏航角速度误差

上述三种不同情况的仿真结果表明，定理1的时延边界计算方法是正确的，所提出的通信时延下UAV/UGV混合编队稳定性分析方法是有效的。

4 结束语

针对通信时延下的高维异构UAV/UGV混合编队控制系统，本文提出了系统稳定的充分必要条件，给出准确时延边界的计算方法。建立了考虑异构特性的UAV/UGV混合编队模型，对UAV群组、UGV群组分别设计了基于信息一致性的分布式控制器。利用矩阵相似变换，将高维异构的UAV/UGV混合编队控制系统进行降维拆分，极大地降低了稳定性分析的解析难度和运算量。证明了只存在一个时延区间可以令编队稳定，并利用辅助特征函数法推导了准确的时延边界。最后，通过三组仿真验证了所提出稳定性分析方法的有效性。