习题“换装”记

环靖

命题人出试题的主要依据就是教材，翻阅历年的中考题，不难看到教材课后练习的身影。同学们平时要弄清教材上的每一个问题，弄清题目背后的目的和考查深意，这样才能举一反三，事半功倍。

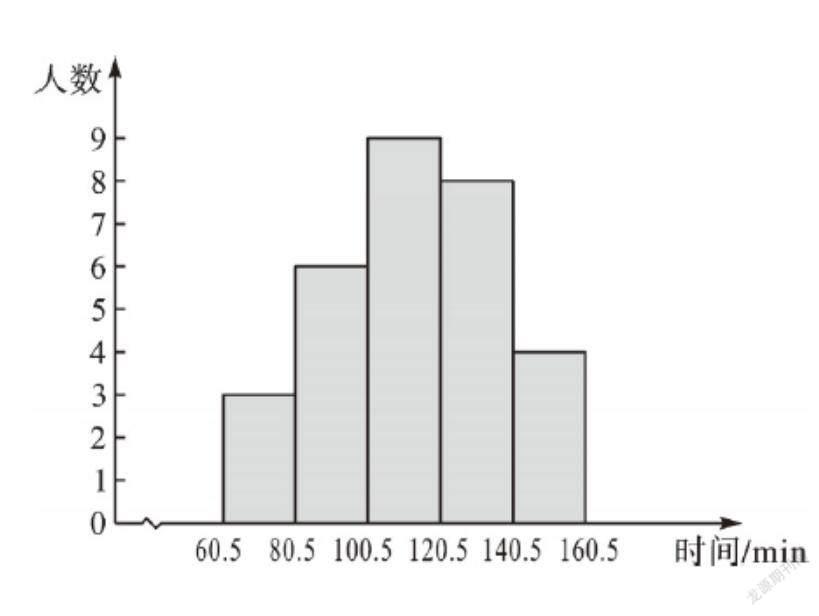
原题 （苏科版数学教材九年级下册第128页练习2）某研究性学习小组采用简单随机抽样的方法，对本校九年级学生一天中做家庭作业所用时间（单位：min）进行了抽样调查，并把所得数据整理后绘制成频数分布直方图。

根据提供的信息回答问题：

（1）该研究性学习小组抽取的样本容量是多少？

（2）在所抽查的学生中，一天做家庭作业所用时间超过120min的频率是多少？

（3）调查所得数据的中位数落在什么范围内？

（4）你对该校九年级学生一天中做家庭作业所用时间做怎样的分析、推断？

解：（1）抽取的样本容量为30;

（2）一天做家庭作业所用时间超过120min的频率为0.4;

（3）调查所得数据的中位数落在100.5～120.5min范围内;

（4）估计该校九年级能在100～120min完成一天的家庭作业的学生人数最多;估计有40%的学生一天中做家庭作业所用的时间超过120min，只有10%的学生能在60～80min完成一天的家庭作业，说明学生的学习负担较重。

换装一：“一个统计图”变成“两个统计图”

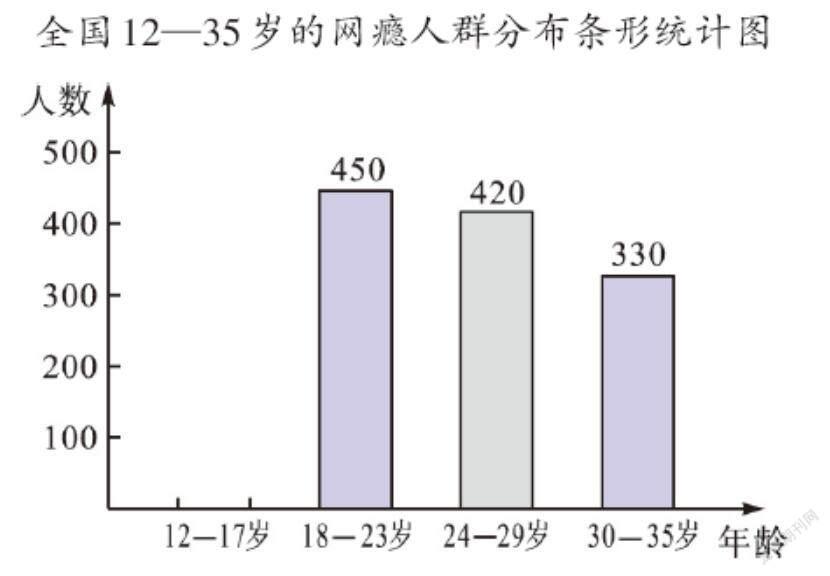
例1 网瘾低龄化问题已经引起社会各界的高度关注，有关部门在全国范围内对12—35岁的网瘾人群进行了简单的随机抽样调查，绘制出以下两幅不完整的统计图。

请根据图中的信息，回答下列问题：

（1）这次抽样调查中共调查了 人，并请补全条形统计图;

（2）扇形统计图中18—23岁部分的圆心角的度数是 ;

（3）据报道，目前我国12—35岁网瘾人数约为2000万，请估计其中12—23岁的人数。

解：（1）这次抽样调查中调查的总人数为330÷22%=1500（人），则12—17岁的人数为1500-（450+420+330）=300（人）。

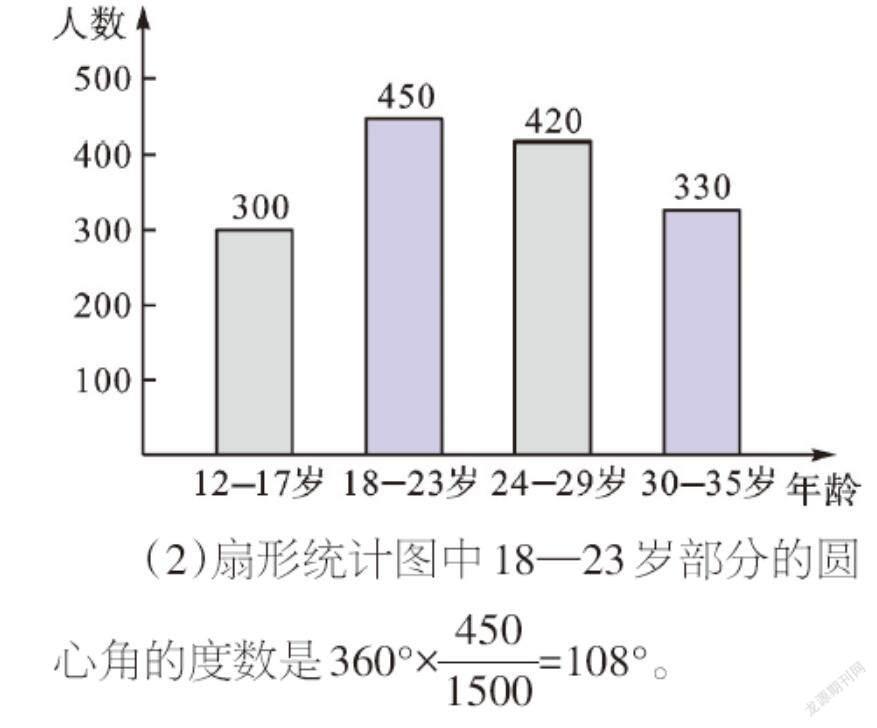
补全条形统计图如下：

（2）扇形统计图中18—23岁部分的圆心角的度数是360°×[4501500]=108°。

（3）估计12—23岁的网瘾人数为2000×50%=1000（万人）。

【点评】同学们要通过两个统计图数据之间的联系找到解决问题的突破口，掌握频率、频数和总数与扇形统计图之间的关系，学会利用样本中的频率估计总体。

换装二：利用范围判断一组数据的极端值

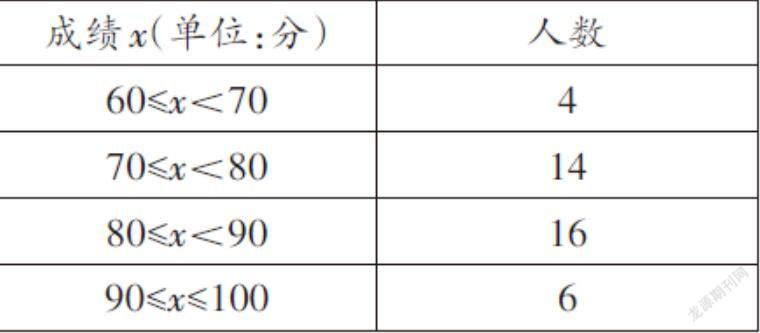
例2 某校九年级（1）班40名同学期末考试成绩统计表如下。

下列结论：①成绩的中位数在80≤x<90;②成绩的众数在80≤x<90;③成绩的平均数可能为70;④成绩的极差可能为40。其中正确结论的序号是 。

解：∵共有40名同学，那么中位数是第20和第21个数的平均数，

∴成绩的中位数在80≤x<90这个范围内，故①正确。

众数不一定在80≤x<90这个范围内，故②不正确。

[60×4+70×14+80×16+90×64+14+16+6]≤x<[70×4+80×14+90×16+100×64+14+16+6]，

∴平均值只可能在76≤x<86这个范围内，

∴成绩的平均数可能为70是错的，故③不正确。

成绩的极差可能为100-60=40，故④正确。

故答案为①④。

【点评】同学们要学会用极端值的思想解决统计问题，一组数据中出现次数最多的数值是众数，而题中的信息是范围，所以在60≤x<70范围内的4人成绩可能一样，在80≤x<90范围内的16人成绩可能在每一个数值上都是平均分布，所以众数不确定。因为题中信息是范围，所以同学们同样可以利用极端值的思想，求出成绩的平均数范围。

换装三：从单一角度分析评价到多角度分析评价

例3 甲、乙两人在相同的情况下各打靶10次，每次打靶的成绩如下（单位：环）：

甲：9，5，7，8，7，6，8，6，7，7;

乙：7，9，6，8，2，7，8，4，9，10。

请你运用所学的统计知识做出分析，从三个不同角度评价甲、乙两人的打靶成绩。

解：从集中趋势看，x甲=7环，x乙=7环，

∴x甲=x乙，即甲、乙两人水平相当。

从离散程度看，s甲2=1.2环2，s乙2=5.4环2，

∴x甲=x乙，s甲2

从最高分看，∵9<10，

∴乙比甲更有潜力。

【点评】同学们要学会从多角度分析评价，可以从集中趋势、离散程度等多方面进行分析评价，但无论从哪一个角度分析，都要有数据作为支撑。从方差角度进行评价的时候，要注意只有在平均數相等或者相差不大的情况下进行分析才合理，离散程度只能反映数据的稳定程度，并不能直接体现水平的高低。

（作者单位：江苏省六合高级中学附属初级中学）