摸球试验“72变”

曹丹

教材是中考试题编者的重要参考内容，很多试题都来源于教材。下面我们来看一个例子，识别中考题中此类题的种种“马甲”。

原题 （苏科版数学教材九年级下册第138页练习2）一只不透明的袋子中装有2个红球和1个白球，这些球除颜色外都相同。

（1）将球搅匀，从中任意摸出1个球，记下颜色后放回、搅匀，再从中任意摸出1个球，求两次都摸到红球的概率;

（2）将球搅匀，从中任意摸出2个球，求摸到2个红球的概率。

【分析】这是一个典型的摸球试验。第（1）问是放回试验;第（2）问摸2个球，相当于第一次摸出的球不放回，第二次再从余下的球中任意摸出1个球，是不放回试验。

解：把2个红球编号为红球1、红球2。

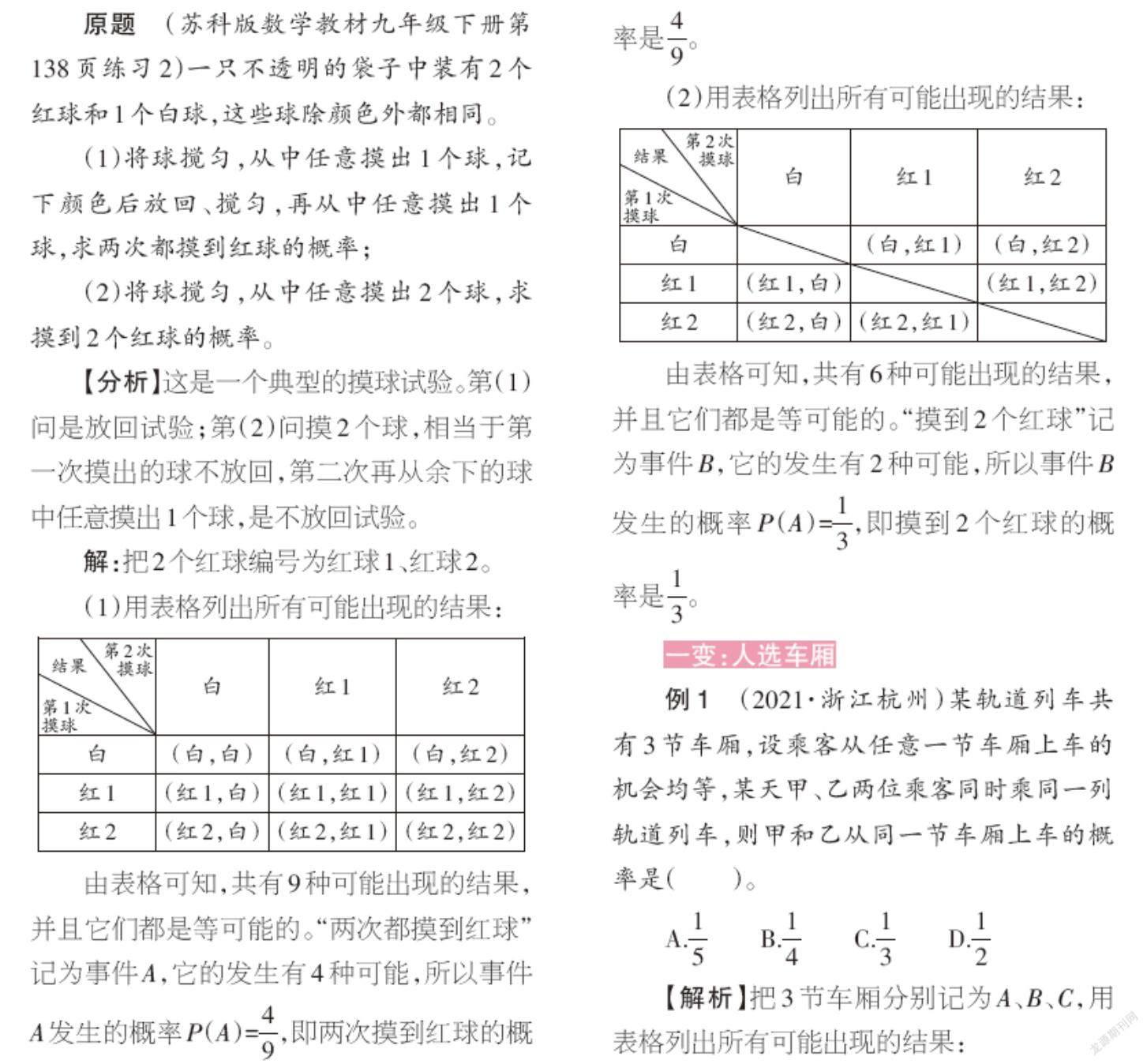
（1）用表格列出所有可能出现的结果：

由表格可知，共有9种可能出现的结果，并且它们都是等可能的。“两次都摸到红球”记为事件A，它的发生有4种可能，所以事件A发生的概率P（A）=[49]，即两次摸到红球的概率是[49]。

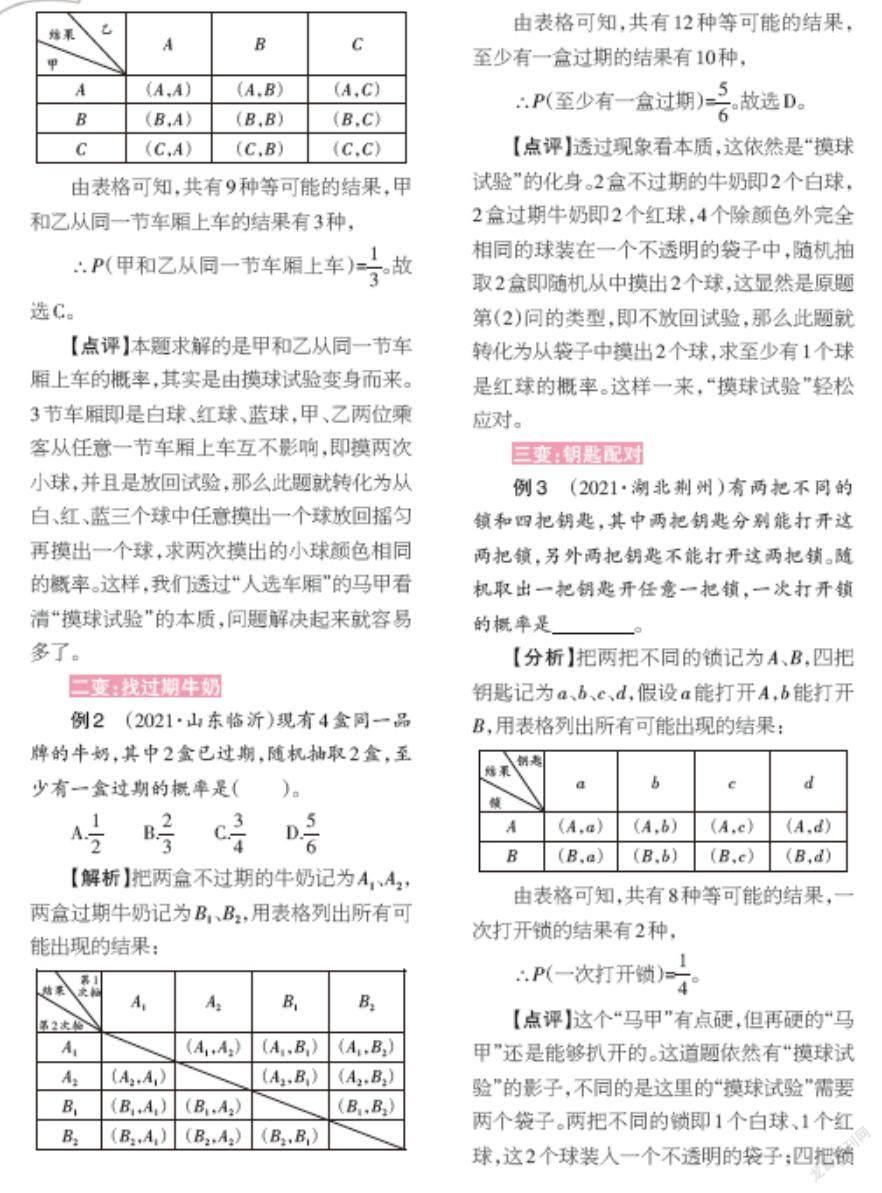
（2）用表格列出所有可能出现的结果：

由表格可知，共有6种可能出现的结果，并且它们都是等可能的。“摸到2个红球”记为事件B，它的发生有2种可能，所以事件B发生的概率P（A）=[13]，即摸到2个红球的概率是[13]。

一变：人选车厢

例1 （2021·浙江杭州）某轨道列车共有3节车厢，设乘客从任意一节车厢上车的机会均等，某天甲、乙两位乘客同时乘同一列轨道列车，则甲和乙從同一节车厢上车的概率是（ ）。

A.[15] B.[14] C.[13]    D.[12]

【解析】把3节车厢分别记为A、B、C，用表格列出所有可能出现的结果：

由表格可知，共有9种等可能的结果，甲和乙从同一节车厢上车的结果有3种，

∴P（甲和乙从同一节车厢上车）=[13]。故选C。

【点评】本题求解的是甲和乙从同一节车厢上车的概率，其实是由摸球试验变身而来。3节车厢即是白球、红球、蓝球，甲、乙两位乘客从任意一节车厢上车互不影响，即摸两次小球，并且是放回试验，那么此题就转化为从白、红、蓝三个球中任意摸出一个球放回摇匀再摸出一个球，求两次摸出的小球颜色相同的概率。这样，我们透过“人选车厢”的马甲看清“摸球试验”的本质，问题解决起来就容易多了。

二变：找过期牛奶

例2 （2021·山东临沂）现有4盒同一品牌的牛奶，其中2盒已过期，随机抽取2盒，至少有一盒过期的概率是（ ）。

A.[12] B.[23] C.[34]    D.[56]

【解析】把两盒不过期的牛奶记为A1、A2，两盒过期牛奶记为B1、B2，用表格列出所有可能出现的结果：

由表格可知，共有12种等可能的结果，至少有一盒过期的结果有10种，

∴P（至少有一盒过期）=[56]。故选D。

【点评】透过现象看本质，这依然是“摸球试验”的化身。2盒不过期的牛奶即2个白球，2盒过期牛奶即2个红球，4个除颜色外完全相同的球装在一个不透明的袋子中，随机抽取2盒即随机从中摸出2个球，这显然是原题第（2）问的类型，即不放回试验，那么此题就转化为从袋子中摸出2个球，求至少有1个球是红球的概率。这样一来，“摸球试验”轻松应对。

三变：钥匙配对

例3 （2021·湖北荆州）有两把不同的锁和四把钥匙，其中两把钥匙分别能打开这两把锁，另外两把钥匙不能打开这两把锁。随机取出一把钥匙开任意一把锁，一次打开锁的概率是 。

【分析】把两把不同的锁记为A、B，四把钥匙记为a、b、c、d，假设a能打开A，b能打开B，用表格列出所有可能出现的结果：

由表格可知，共有8种等可能的结果，一次打开锁的结果有2种，

∴P（一次打开锁）=[14]。

【点评】这个“马甲”有点硬，但再硬的“马甲”还是能够扒开的。这道题依然有“摸球试验”的影子，不同的是这里的“摸球试验”需要两个袋子。两把不同的锁即1个白球、1个红球，这2个球装入一个不透明的袋子;四把锁即白、红、黄、蓝各1个球，这4个球装入另一个不透明的袋子，这些球除颜色外都相同。随机取出一把钥匙开任意一把锁即从这2个袋子中分别取出1个球，这种“摸球试验”还是摸两次，不过是从两个袋子各摸一次，那么就转化为从2个袋中分别取出1个球，求2个球颜色相同的概率。这样思考，简单明了。

这里虽然只举出了三种变化方式，但是实际上摸球试验通过“72变”甚至“108变”还是可以变出许许多多的样子。希望同学们可以看透本质，回归“摸球试验”模型，提高解决问题的能力。

（作者单位：江苏省南京市六合区横梁初级中学）