抓住结合点 巧读统计图

汪宏玲

人类的生活进入了“大数据时代”，一切用数据说话，如何解读数据与我们每个人的生活息息相关。今天我们就来利用三个活动探索如何解读数据。

活动一：折线统计图与统计表相结合（出行交通情境）

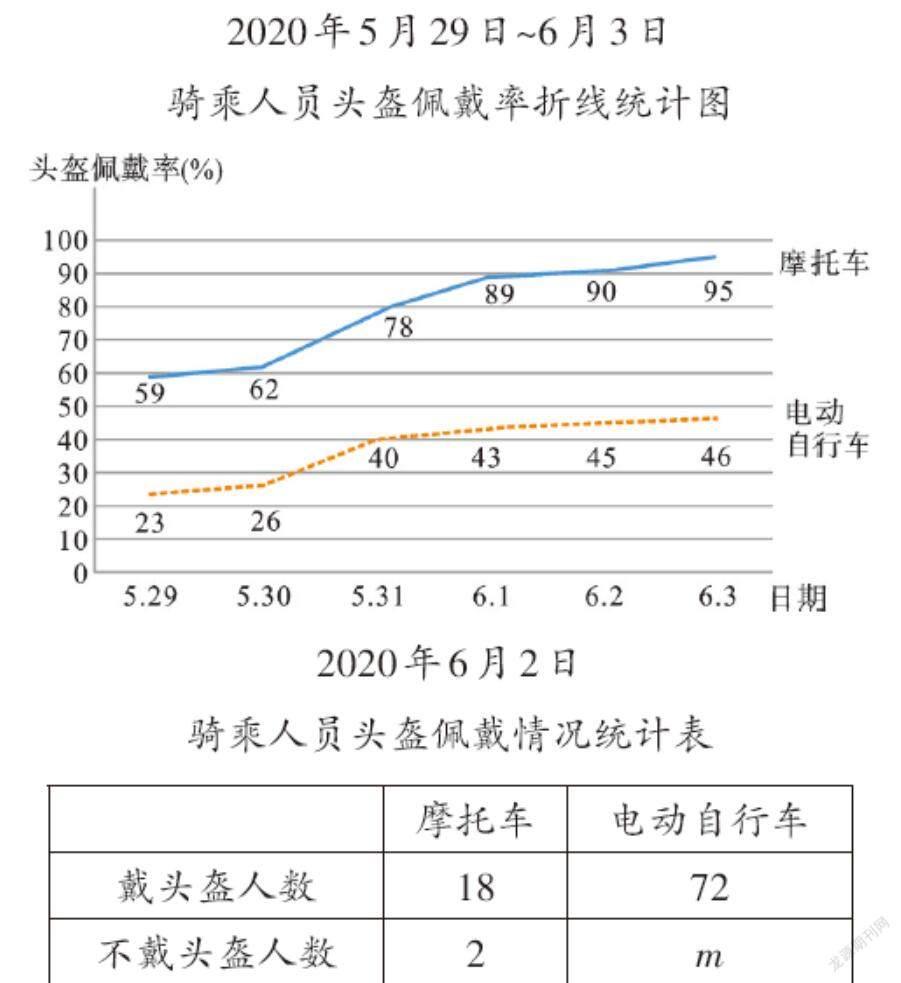
例1 2020年6月1日起，公安部在全国开展“一盔一带”安全守护行动。连续6天，在同一时段对某地区一路口的摩托车和电动自行车骑乘人员佩戴头盔情况进行了调查，并将数据绘制成图表如下：

2020年5月29日～6月3日

2020年6月2日

（1）根据以上信息，小明认为6月3日该地区全天摩托车骑乘人员头盔佩戴率約为95%。你是否同意他的观点？请说明理由;

（2）求统计表中m的值;

（3）相比较而言，你认为需要对哪类人员加大宣传引导力度？为什么？

【解析】解决这类问题的诀窍是要明白几个问题：（1）样本要具有代表性、普遍性;（2）能从两幅图表中提取相关的有效数据，如本题6月2日对应的电动自行车头盔佩戴率为45%，就能用当天骑乘电动自行车头盔佩戴的72人算出骑乘电动自行车的总人数;（3）用数据说话，回答第3个问题时如果泛泛而谈，没有从本题的数据出发，比如要加强头盔佩戴宣传等，这种答案是无意义的。可参考如下回答：由折线统计图可知，连续6天电动自行车骑乘人员头盔佩戴率比摩托车骑乘人员头盔佩戴率要低很多，电动自行车骑乘人员头盔佩戴率最高仅有46%，应对电动自行车骑乘人员加大宣传引导力度。

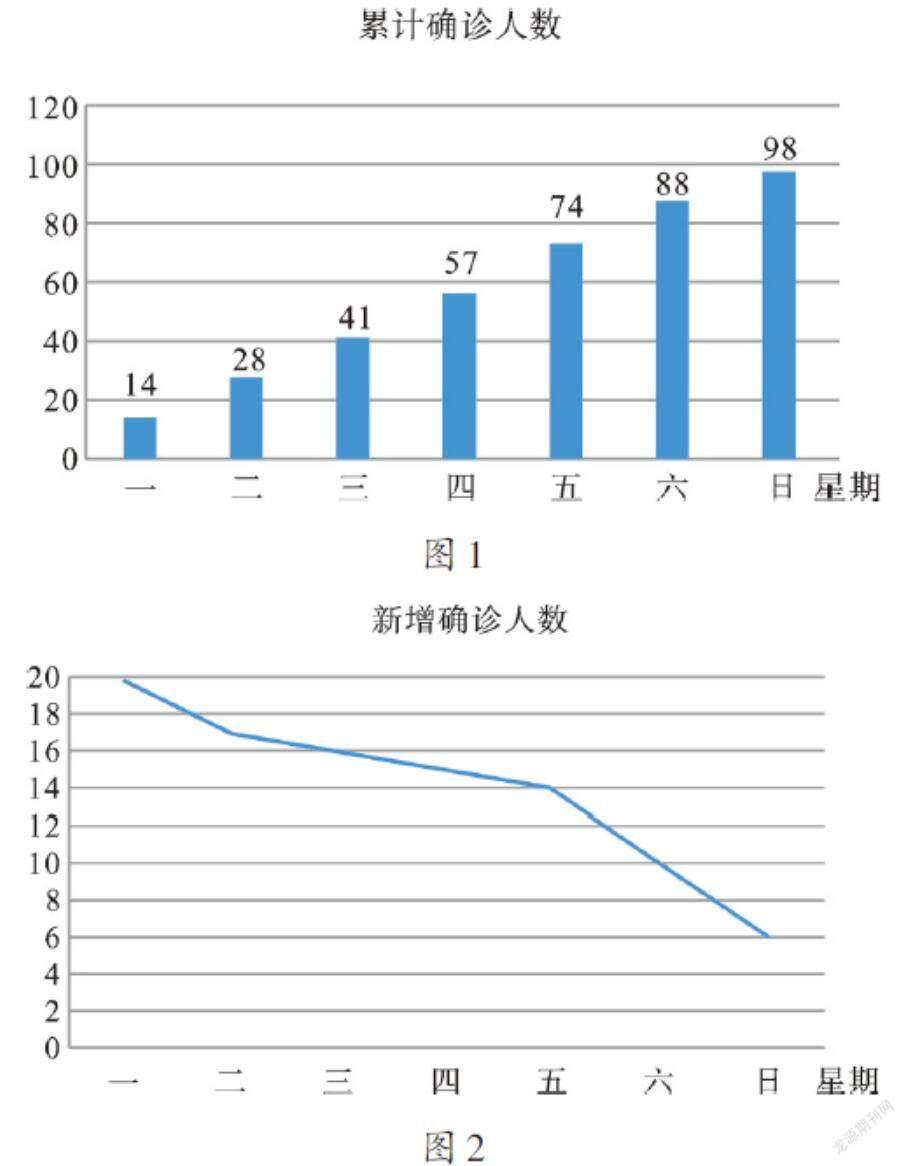
活动二：条形统计图与折线统计图相结合（全民抗疫情境）

例2 在某次疫情发生后，根据疾控部门发布的统计数据，绘制出如下统计图：图1为A地区累计确诊人数的条形统计图，图2为B地区新增确诊人数的折线统计图。

（1）根据图1中的数据，A地区星期三累计确诊人数为 ，新增确诊人数为 ;

（2）已知A地区星期一新增确诊人数为14人，在图2中画出表示A地区新增确诊人数的折线统计图。

（3）你对这两个地区的疫情做怎样的分析、推断？

【解析】统计学的每一个情境都来源于生活，又服务于生活。解决这类问题的诀窍：（1）对两幅图中有效信息进行提炼与整合;（2）要逐步培养样本估计总体的统计学思想。第（3）问依然不能单纯凭借生活经验作答，要厘清题意，根据问题回答。如A地区疫情不断反复，如果不加以有效控制，A地区累计确诊人数可能会持续增加;B地区新增确诊人数有减少趋势，说明疫情控制情况较好。

活动三：散点图与统计表相结合（垃圾分类情境）

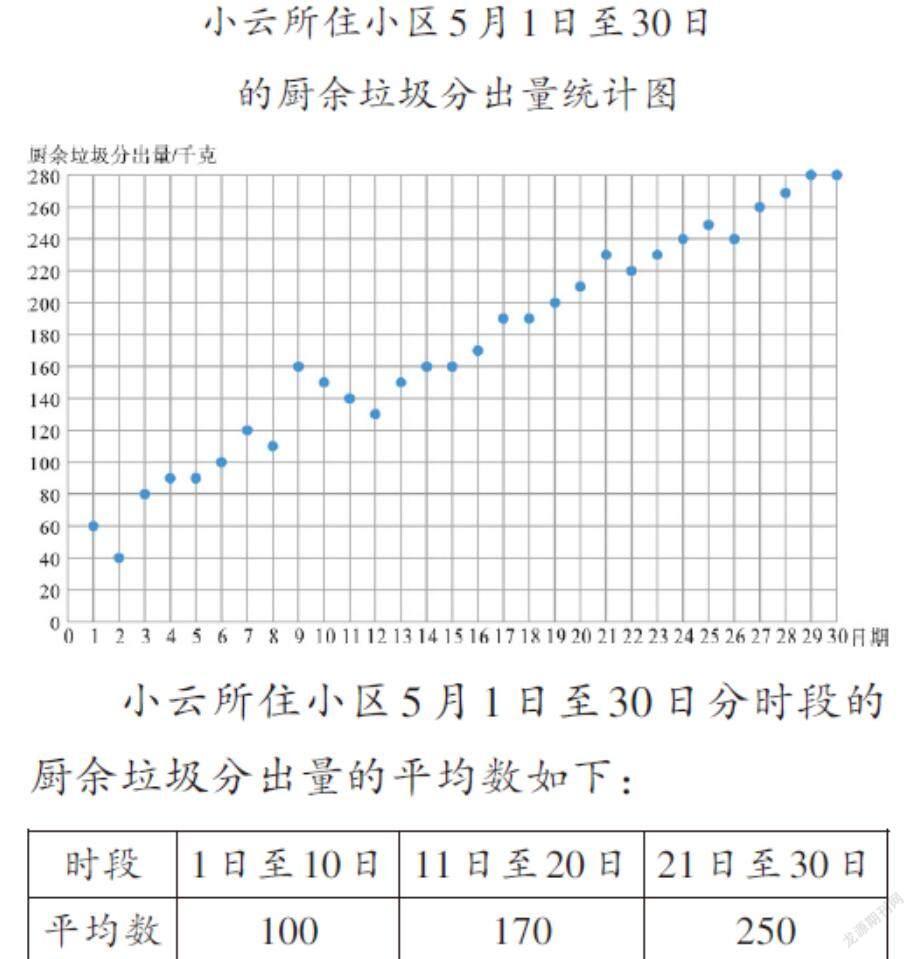
例3 小云统计了自己小区5月1日至30日的厨余垃圾分出量（单位：千克），信息如下：

小云所住小区5月1日至30日分时段的厨余垃圾分出量的平均数如下：

（1）已知该小区5月31日厨余垃圾分出量为261千克，则5月该小区的厨余垃圾分出量的平均数约为 ;

（2）记该小区5月1日至10日厨余垃圾分出量的方差为s12，5月11日至20日的厨余垃圾分出量的方差为s22，5月21日至30日的厨余垃圾分出量的方差为s32。直接写出s12、s22、s32的大小关系。

【解析】这类题统计图复杂、计算烦琐，但同学们不要有畏惧心理，根据前两个活动总结的经验，可迁移来解决这个问题。第（1）问有很多同学这样计算[100+170+250+2614]，其实这里是考查统计量中算术平均数与加权平均数的区别，100、170、250的权重都为10，而261的权重为1。第（2）问考查的是另一个统计量方差。我们知道，方差反映数据的稳定程度，散点图能直观反映数据的离散程度。无须计算，在三个时间段中分别画出平均数这条线（如图3），通过每个数据与平均数的距离远近就能读出s12>s22>s32，这就是巧读统计图的奥妙。

通过上面的活动，老师希望大家能初步培养数据分析的观念，读懂具有相关性的统计图表。大数据时代，数据的收集、整理不成问题，怎样将数据的效用最大化才是我们每个同学都要为之努力的。了解统计学知识，你会成为当今时代的明白人。

（作者单位：江苏省金陵中学仙林分校中学部）