几何非线性黏性阻尼隔振系统动力学特性研究

刘海超，金映丽，闫 明，孙自强，惠安民，王开平

（沈阳工业大学机械工程学院，辽宁 沈阳 110870）

引 言

随着中国舰船制造技术的快速发展，舰载设备日益精密化、智能化，但其所处的工作环境却日益复杂和严酷，这对舰载设备隔振装置的设计提出了更高的标准与要求［1-2］。由于舰船上多为大型重载设备，所以隔振器应具有更高的承载能力和更低的隔振频率，显然线性隔振器已经不能满足工程实际需求，因此，近年来国内外学者对非线性隔振系统展开了广泛而深入的研究。

陆泽琦等［3］对近年国内外多种非线性隔振系统的理论与应用进行了综述，非线性刚度能够有效解决线性隔振系统承载能力不足的问题。Brennan等［4］采用谐波平衡法求解了具有软化和硬化的Duffing 隔振系统响应方程，研究了跳降频率和跳升频率与系统参数的关系。张小龙等［5］进一步推导了Duffing 型隔振系统跳跃频率和力传递率的计算公式，分析了隔振系统主要参数对力传递率影响规律。文献［6-10］采用了理论、仿真和试验的方法对准零刚度隔振器的非线性动力学行为进行了研究，结果表明，准零刚度隔振器的高静低动特性使隔振系统具有更高的承载能力、更优的隔振带宽，但只适用于小幅值振动。Li 等［11-12］设计了一种双腔固液混合（SALiM）隔振器，通过理论计算与振动试验对系统非线性刚度和阻尼特性进行了研究，这种隔振器更适合低频重型设备的隔振。Gao 等［13］为低频重型设备设计了一种具有高静态和低动态（HSLD）刚度的新型油气近零频率（NZF）隔振器，该隔振器通过调节气压改变承载能力，采用流体阻尼机构实现了阻尼非线性。

相比线性隔振器，准零刚度隔振器虽然可以实现较高的承载能力和较低的隔振频率，但由于刚度的非线性常常会导致系统出现跳跃、分岔和混沌等不稳定现象。目前常采用提高系统阻尼来改善隔振系统的动力学性能。Kovacic 等［14］对具有非线性阻尼的三类Duffing 隔振系统（渐软、渐硬和双稳）的动力学特性进行研究，得出了幂函数非线性阻尼对分岔结构和通向混沌途径的依赖与系统的非线性刚度特征；并且对于渐软系统，随着激励幅值增加，下跳频率对阻尼的非线性阶次较为敏感，因此可以通过增加阻尼阶次提高系统的稳定性。Sharma 等［15］分析了非线性阻尼对强迫Duffing 系统的分岔与混沌特性的影响，结果表明，非线性阻尼能够降低系统首次进入混沌状态的临界值，增加发生混沌的参数空间，影响系统进入混沌的通道。Ho 等［16］首次采用输出频响函数法分析了非线性刚度和非线性阻尼对Duffing 系统动态行为的影响，结果表明，非线性阻尼对抑制隔振系统共振峰值，提高系统稳定性的效果要远优于线性阻尼。Peng 等［17］采用谐波平衡法研究了立方阻尼对非线性隔振系统动力学特性的影响，结果表明立方阻尼隔振器在一些特殊情况下才具有优势。Laalej 等［18］利用主动试验装置对立方阻尼隔振系统进行了试验研究，结果充分说明了通过在单自由度隔振系统中使用三次非线性阻尼可以获得较好隔振效果。苏何先等［19］通过对非线性黏滞阻尼器进行性能试验测试进一步明确了非线性阻尼器的关键参数，有助于设计出更符合工程实际需求的非线性阻尼器。

考虑舰载设备复杂的工作环境，被动隔振方式依然是首要选择，为了提高非线性隔振系统的振动性能，本文采用线性黏性阻尼器与隔振系统运动方向垂直的布置形式实现了系统阻尼的几何非线性；采用平均法求解了非线性隔振系统的主共振响应，分析了线性阻尼、库伦阻尼和几何非线性黏性阻尼对系统幅频响应、稳定性的影响规律，并且实现了隔振系统参数的避跳设计；最后通过振动试验进一步验证了几何非线性黏性隔振系统的特性规律。

1 建立隔振系统模型

1.1 系统力学模型

几何非线性隔振系统力学模型如图1所示。M为设备的质量，K1和K2分别为隔振器垂向线性刚度和非线性刚度系数，C1为垂向线性黏性阻尼系数，Ff为垂向库伦阻尼力，C2为水平线性黏性阻尼系数，D为水平阻尼器初始长度，Y（t）和X（t）分别代表基座和设备的绝对位移。

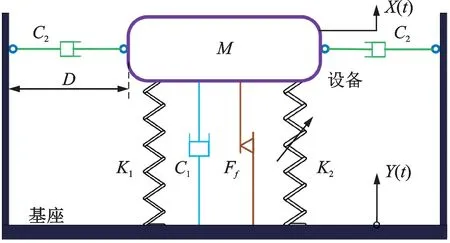
图1 几何非线性隔振系统力学模型Fig.1 Mechanical model of geometrically nonlinear vibration isolation system

1.2 系统数学模型

几何非线性隔振系统随基础激励做受迫振动，假设基础激励为谐波信号，即Y（t）=Psin（ωt），定义设备与基座的相对位移Z（t）=X（t）−Y（t）。

系统中的弹性力和阻尼力分别表示为：

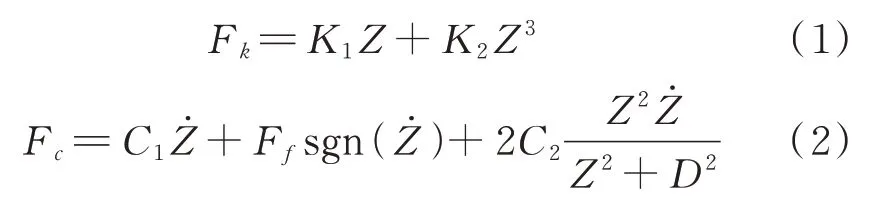
当Z≤0.2D时，利用泰勒级数展开将式（2）简化为：

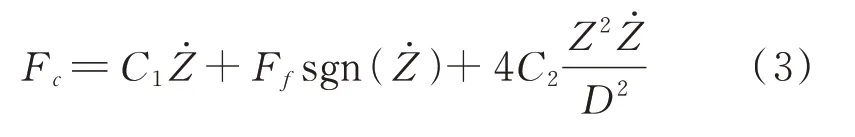
由此，系统的动力学方程为：

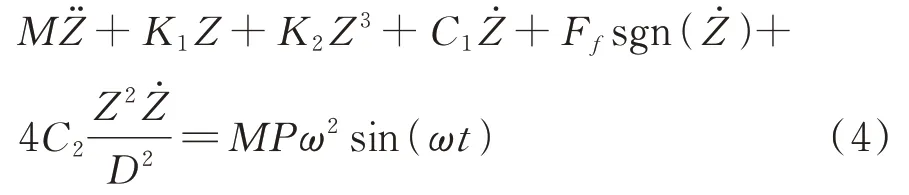
定义无量纲参数如下：

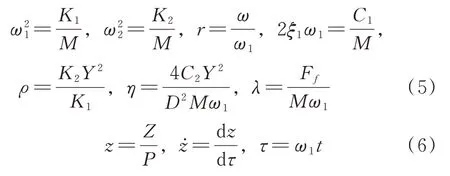
变换得到相对坐标系下动力学方程（4）的无量纲形式为：

2 幅频响应特性分析

假设系统稳态响应的一次近似解为：

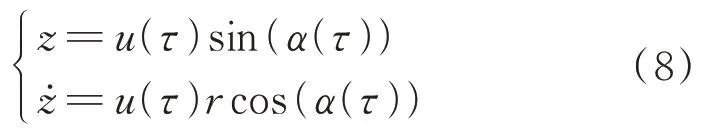
式中u(τ)为无量纲振动幅值，α(τ)=rτ+θ(τ)，θ(τ)为无量纲相位角，由此推出：

同时，利用傅里叶展开对sgn 函数进行化简，有：

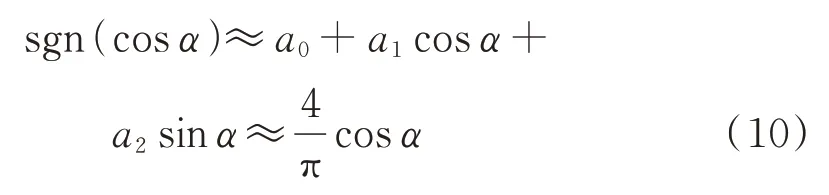
将式（8）～（10）代入式（7）求出关于和的方程式为：

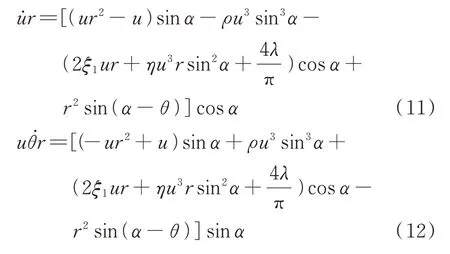
其中，根据三角函数化简关系有：

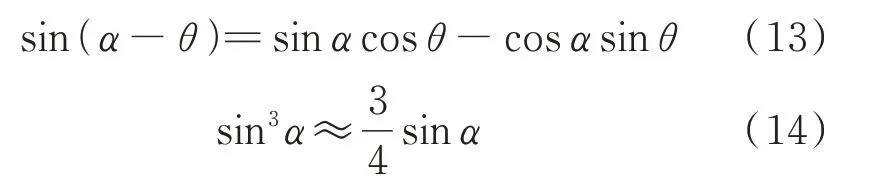
将式（13）和（14）代入式（11）和（12）整理得到：

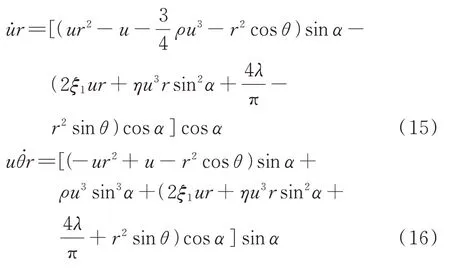
由于和为随时间缓慢变化的周期量，因此采用平均法求得一个周期内的平均值为：

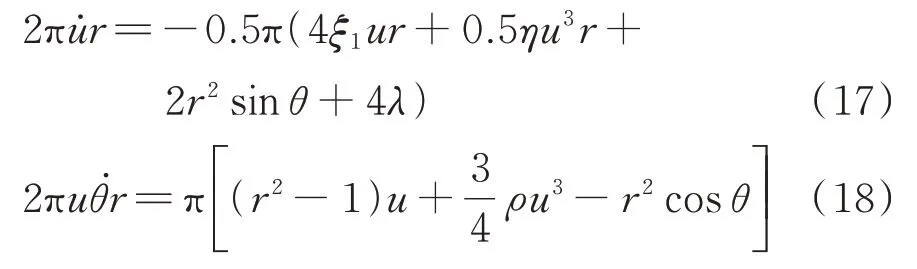
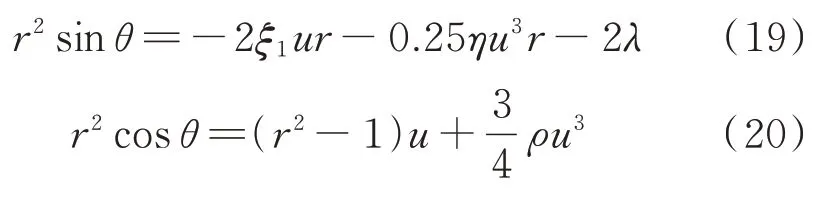
将式（19）和（20）两边平方求和，整理得到系统幅频响应和相频响应方程：

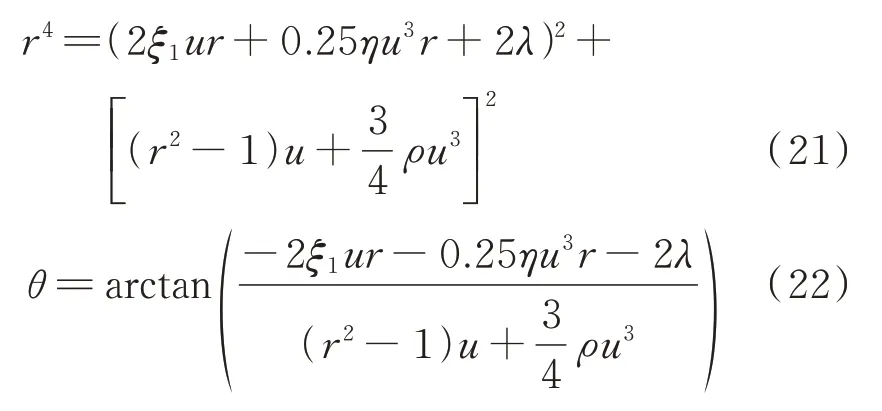
由式（21）得到系统的骨干曲线方程：

如图2所示，分别绘制了线性隔振系统与Duffing 隔振系统的无量纲幅频特性曲线，其中，骨干线由式（23）绘制。图3～5 分析了线性阻尼ξ1、库伦阻尼λ和几何非线性黏性阻尼η对软、硬特性隔振系统的幅频响应特性的影响规律。

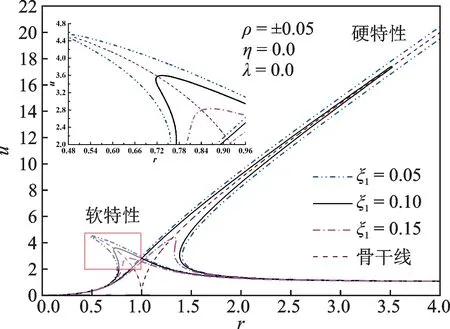
图3 参数ξ1对幅频特性曲线的影响Fig.3 The influence of parameter ξ1 on the amplitudefrequency characteristic curve

由图3可知，随着线性阻尼ξ1增加，软、硬隔振系统的幅频响应峰值都会大幅降低，跳跃区间迅速减小，直到跳跃现象完全消失。

由图4可知，由于库伦阻尼力的“锁定”特性（即由于库伦阻尼具有黏滞作用，当振动频率较低时，系统具有保持初始静止状态的特性），幅频响应的曲线起始频率（逃离频率）大于零，并随着λ的增大向右移动。对硬特性非线性隔振系统，当库伦阻尼λ≤0.5 时，库伦阻尼对幅频响应的影响较小，当库伦阻尼λ>0.5 时，幅频特性响应曲线逃离频率r>1.0，此时幅频特性响应曲线出现独立封闭环形区域，即“频率岛”现象［20］，并且“频率岛”内部区域均为不稳定的跳变区，随着库伦阻尼的增大，“频率岛”缓慢减小直到消失，此时系统才恢复稳定状态；对于软特性非线性隔振系统，随着库伦阻尼的增大，幅频响应峰值迅速衰减，跳跃现象消失，因此，增加库伦阻尼有利于提高软特性非线性隔振系统的稳定性。

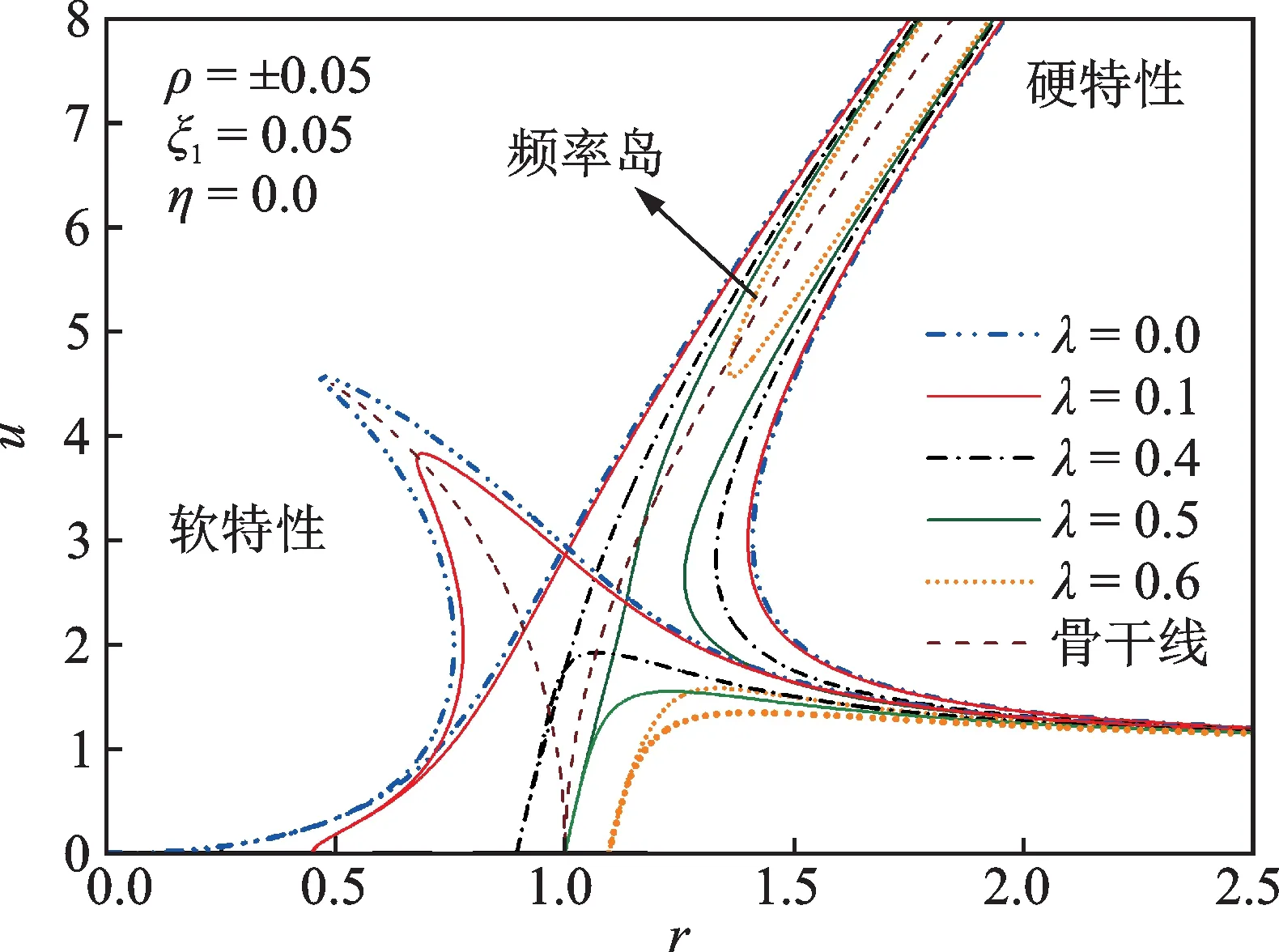
图4 参数λ 对幅频特性曲线的影响Fig.4 The influence of parameter λ on the amplitudefrequency characteristic curve

由图5可知，微量增加几何非线性黏性阻尼η，软、硬特性隔振系统的幅频响应峰值大幅下降，跳跃现象迅速消失，同时不会因为η的增加导致幅频响应曲线出现“频率岛”现象。因此，几何非线性黏性阻尼对降低软、硬特性隔振系统的幅频响应，提高系统稳定性起到了十分重要的作用。

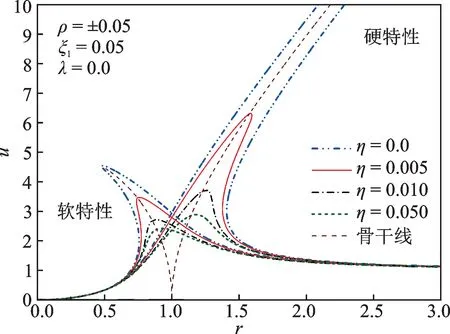
图5 参数η 对幅频特性曲线的影响Fig.5 The influence of parameter η on the amplitudefrequency characteristic curve

3 定常解稳定性分析

为了研究非线性隔振系统定常解的稳定性，将表达式u=u0+v（τ）和θ=θ0+φ（τ）代入式（17）和（18），考虑式（19）和（20）的定常解并进行线性化处理得到扰动方程：

其中：

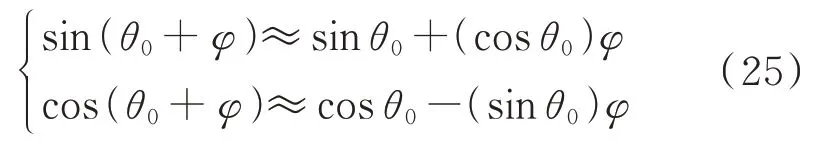
u0和θ0为式（19）和（20）的定常解，v（τ）和φ（τ）是两个较小的扰动。

设方程（24）的解为v=v0est和φ=φ0est，得到特征方程为：

总的来说，选择关键词作文相对学生平时练的其他任务驱动型作文是更为容易，出现偏题离题的现象也更少，学生也较难拉开作文的差距。但如果在大部分学生没关注的地方花更多心思，在同样的语言水平、用例丰富程度上，把大家都忽略的关联部分做得更好，同样也可以得到一篇高分的作文。

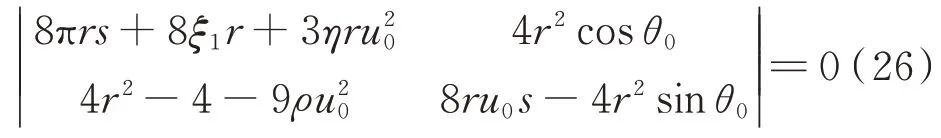
展开行列式得：

根据Routh-Hurwitz 定理，定常解稳定的边界条件为：

图6为不同激励幅值对系统幅频响应及稳定性边界的影响，其中，定义实际施加的位移激励幅值p=nP，n为倍数参数，图中阴影部分为不稳定区域。图7～9 分别研究了线性阻尼ξ1、库伦阻尼λ和几何非线性黏性阻尼η对软、硬特性隔振系统稳定性的影响。

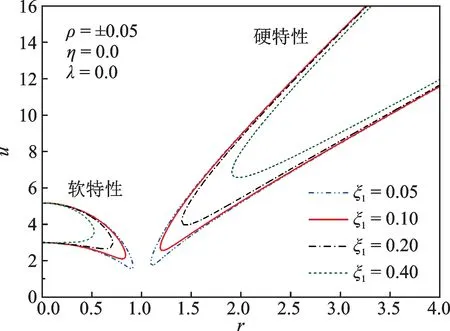
图7 参数ξ1对不稳定区域的影响Fig.7 The influence of parameter ξ1 on unstable region

由图6可知，硬特性非线性隔振系统随激励幅值增加，幅频响应曲线逐渐向右弯曲，共振频率右移，系统隔振频宽减小；软特性非线性隔振系统随激励幅值增加，幅频响应曲线逐渐向左弯曲，共振频率左移，提高了系统隔振范围。但是，无论软、硬隔振系统，不稳定区域的边界由系统参数唯一确定，与激励幅值无关。但随着激励幅值增大，幅频响应曲线落入不稳定区域的部分增加，导致系统不稳定性增加。

图6 不同激励幅值下的幅频响应及稳定边界Fig.6 Stability boundary and amplitude frequency responses with different excitation forces

由图7可知，随线性阻尼ξ1的增加，软、硬特性非线性隔振系统的不稳定区域均逐渐减小，系统稳定性增加。

由图8可知，增加库伦阻尼λ同样可以减小软、硬特性非线性隔振系统的不稳定区域，提高系统稳定性，但是作用效果远远弱于线性阻尼。结合图4，增加库伦阻尼λ能够有效降低软特性非线性隔振系统的幅频响应，而且不会导致“频率岛”现象的出现。因此，在软特性非线性隔振系统中增加库伦阻尼有利于提高系统的稳定性。

图8 参数λ 对不稳定区域的影响Fig.8 The influence of parameter λ on unstable region

由图9可知，随几何非线性黏性阻尼η的增加，硬特性非线性隔振系统不稳定区域快速减小，系统稳定性大幅提高，但是软特性非线性隔振系统不稳定区域变化不大，因此，几何非线性黏性阻尼η更适合应用于硬特性非线性隔振系统减小其跳跃区间，提高系统稳定性能。

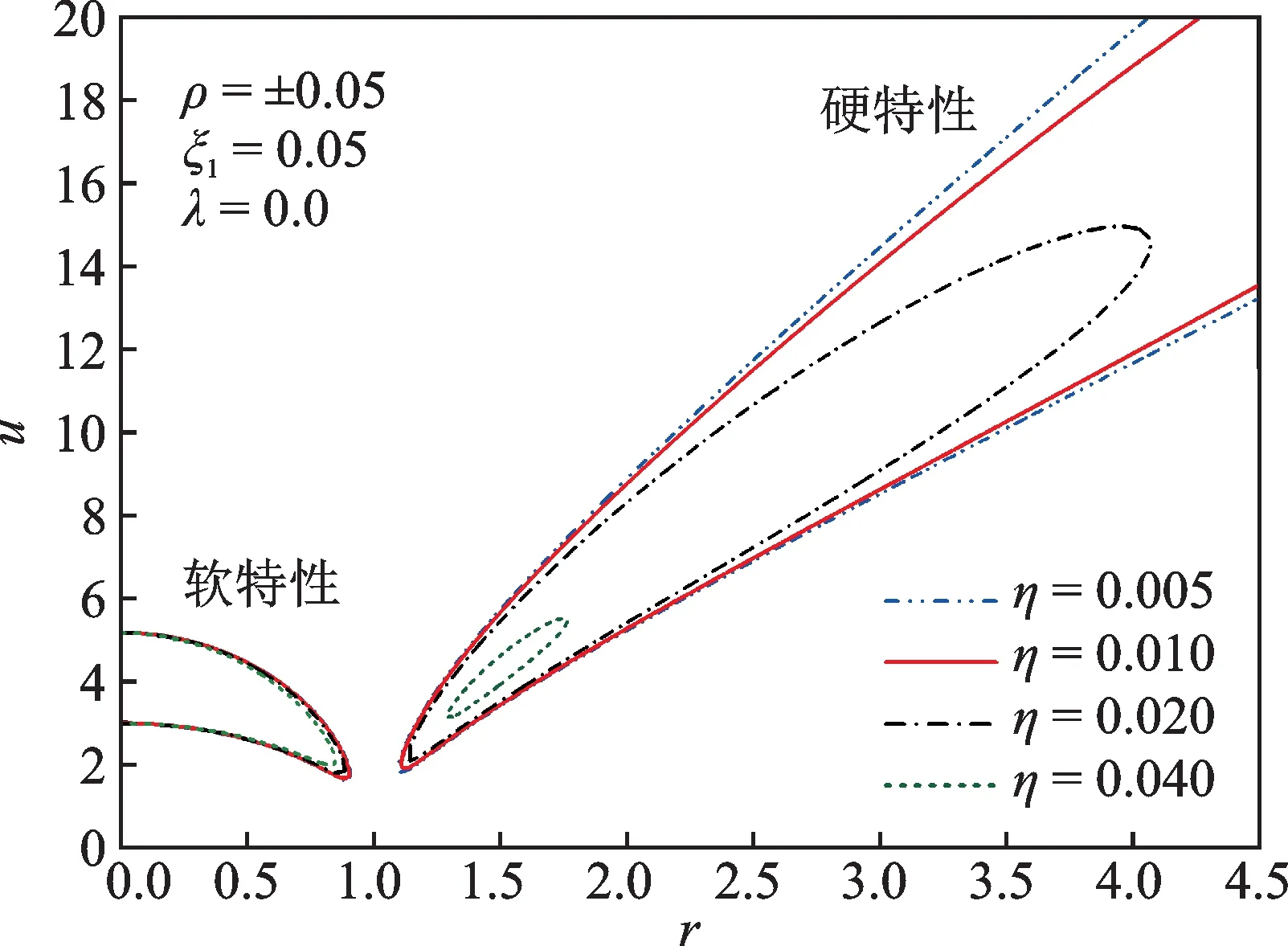
图9 参数η 对不稳定区域的影响Fig.9 The influence of parameter η on unstable region

4 避跳参数设计

通过上述分析，在一定参数范围内会出现对系统造成意外损坏的跳跃现象，故在设计隔振系统参数时应该首先避免跳跃现象的产生。事实上，如果能够保证系统的频率响应是唯一的就可以避免出现跳跃现象［21］，因此，存在一个参数边界将单个和多个幅值区分开，即将跳跃区与非跳跃区分开。结合式（28）和（21）便可得到关于系统参数ρ，ξ1，λ和η的跳跃区和避跳区的边界。

为了避免跳跃现象的产生，对某线性阻尼ξ1=0.05 的软、硬隔振系统的ρ，λ和η参数进行设计，由满足式（28）和（21）的参数构成如图10和11 所示的曲面图，其中曲面及以上的区域为避跳区域，曲面上的星号（*）点为满足避跳边界条件的曲面内插点。图12和13 分别为硬、软特性隔振系统跳跃避免参数的二维图。

图10 硬特性隔振系统跳跃避免边界曲面图Fig.10 Jump avoidance boundary surfaces of the hard characteristic vibration isolation system

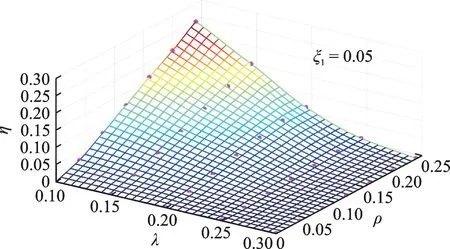
图11 软特性隔振系统跳跃避免边界曲面图Fig.11 Jump avoidance boundary surfaces of the soft characteristic vibration isolation system

图12 硬特性隔振系统跳跃避免参数二维图Fig.12 Two-dimensional diagram of jumping avoidance parameters of hard characteristic vibration isolation system

由图12可知，对于硬特性非线性隔振系统，随着非线性刚度ρ的增加，需要增加更多的几何非线性黏性阻尼η使系统处于避跳区域，即二者呈正相关，并且增加库伦阻尼能够减小避跳所需的几何非线性黏性阻尼η值，增大系统稳定避跳区域。但是，由于库伦摩擦阻尼的“锁定”特性导致了避跳参数设计更加复杂。当λ≤0.5 时，由于库伦阻尼“锁定”频率段较小，非线性刚度ρ与几何非线性黏性阻尼η近似呈线性关系，这大大简化了避跳参数的设计；当λ>0.5 时，随着库伦阻尼增大，逃离频率逐渐向右移动，并且在“锁定”频率段内不需要提供几何非线性黏性阻尼便可以避免跳跃，当频率超过“锁定”频率范围，随着非线性刚度的增加，非线性阻尼会呈现先快速上升（如图12中虚线圆圈包围的频率范围），然后近似线性增长的变化趋势。

由图13可知，对于软特性非线性隔振系统，几何非线性黏性阻尼η随非线性刚度ρ的增加近似线性增加，并且随着库伦阻尼λ的增加，避跳边界所需的几何非线性黏性阻尼逐渐减小，跳跃区间随之减小，系统稳定性增加。因此，对任一非线性刚度ρ，增加几何非线性阻尼η与库伦阻尼λ均能够有效增大避跳区域，提高软特性非线性隔振系统的稳定性。

图13 软特性隔振系统跳跃避免参数二维图Fig.13 Two-dimensional diagram of jumping avoidance parameters of soft characteristic vibration isolation system

5 非线性隔振系统振动试验

5.1 试验装置及工作原理

为了验证上述几何非线性黏性阻尼隔振系统的动力学特性，设计制作了如图14所示的试验装置，主要由基座、水平阻尼器支座、导向装置、传感器测量装置、线性弹簧、垂向黏性阻尼器、质量块、水平黏性阻尼器和磁性弹簧元件组成。该试验装置工作原理为：由图14中的磁性弹簧元件提供非线性刚度，其中磁性弹簧元件是由两对径向磁化的环形永磁体组成，其结构形式如图15所示，具体参数如表1所示。内磁体安装在竖直连杆上并与基座连接固定，外磁体通过上、下端盖与质量块相连并随之运动，由于内外磁体的磁化方向相反，因此，始终存在一个与质量块运动方向相同的磁性力作用在质量块上。磁性弹簧的工作原理、磁性力和磁刚度的计算方法详见文献［22］，由此得到了磁刚度Km的近似计算公式如下：

表1 磁弹簧参数Tab.1 Parameters of the magnetic spring

图14 几何非线性黏性阻尼隔振系统试验装置Fig.14 The test device of geometrically nonlinear viscous damping vibration isolation system test device

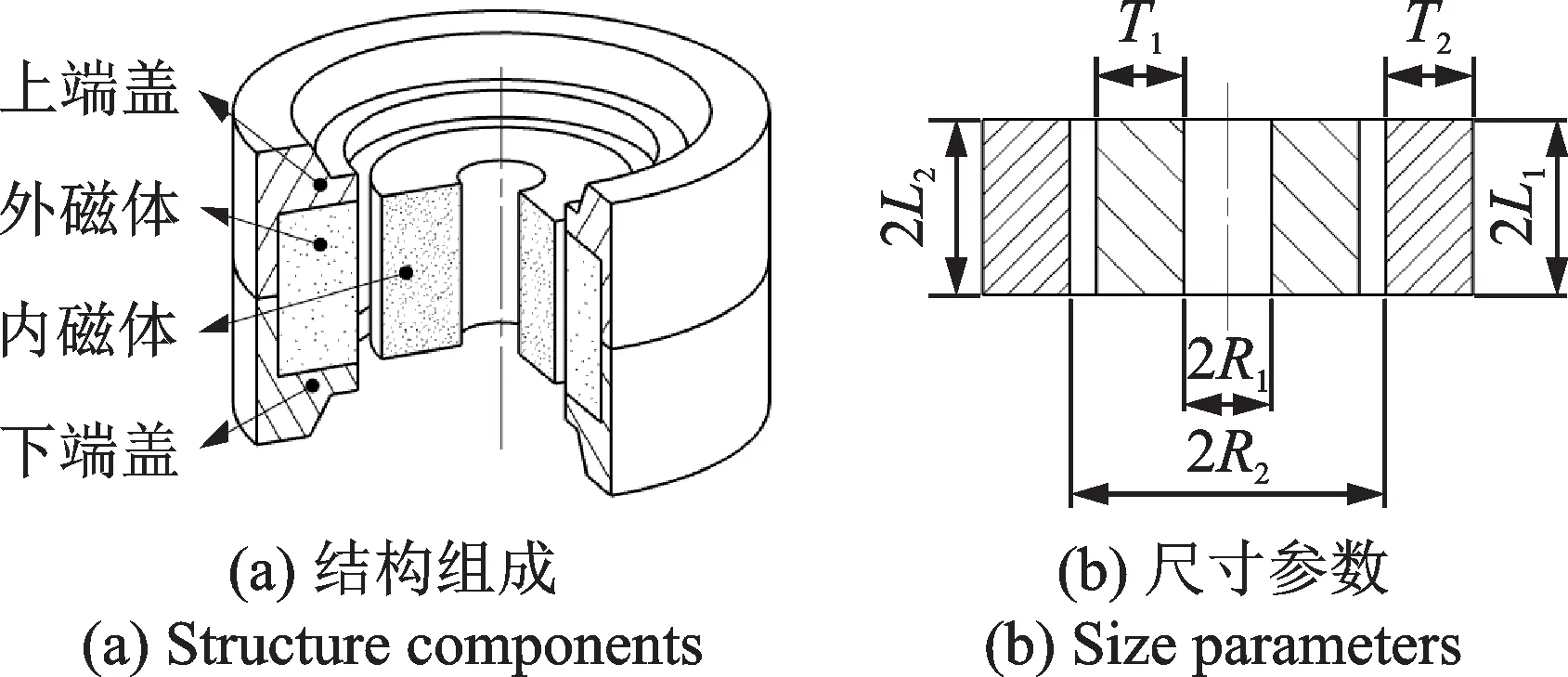
图15 磁性弹簧元件Fig.15 The magnetic spring element

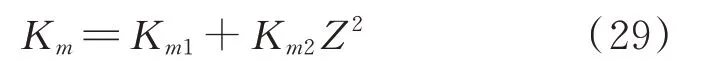
式中Km1和Km2分别为常数项和二次项刚度系数。

由图14中线性弹簧的线性刚度KL和磁性弹簧磁刚度的常数刚度Km1共同提供线性刚度，由此可得：

由图14中垂向黏性阻尼器提供垂向阻尼C1，由水平阻尼器提供几何非线性阻尼C2，由试验装置各部件之间的干摩擦力提供库伦阻尼力Ff。并且采用位移传感器、加速度传感器和数据采集仪采集与记录试验数据。

采用垂向液压振动试验台进行振动试验，试验台基本参数为：最大推力100 kN，正弦扫频范围0.1～160 Hz，试验装置安装及试验系统组成如图16所示。

图16 试验装置安装图Fig.16 The installation diagram of test device

5.2 振动试验及结果分析

以线性隔振系统和硬特性隔振系统为例进行了定频振动试验，频率范围为0.6～15 Hz，频率间隔为0.6 Hz，加载谱位移峰峰值为2 mm，非线性隔振系统的参数如表2所示，试验结果与理论计算幅频响应对比曲线如图17所示。

表2 非线性隔振系统参数Tab.2 Nonlinear vibration isolation system parameters

由图17（a）可知，原系统参数下非线性隔振系统具有硬刚度特性，幅频响应曲线向右弯曲，出现了跳跃现象，并且理论计算与振动试验所得幅频响应曲线具有较好的一致性，最大误差仅为2.5%。

采用第4 节中避跳设计方法对非线性系统进行避跳设计，在其他参数不变的条件下，几何非线性黏性阻尼η=0.09 为避跳临界参数（此时C2=1.50×106N/（m/s）），因此水平黏性阻尼器阻尼系数调到1.66×106N/（m/s），即对应无量纲阻尼系数η=0.10 进行理论计算与振动试验，结果如图17（b）所示。

由图17中（b）可知，当无量纲阻尼系数η超过避跳临界阻尼系数0.09 时，理论计算与振动试验幅频响应曲线均未出现跳跃现象，这说明第4 节中的避跳设计方法具有一定的准确性与普适性，可以用于非线性隔振系统参数设计。

图17 试验结果与理论计算对比分析Fig.17 The comparative analysis of experimental results and theoretical calculations

6 结 论

（1）增加线性阻尼ξ1能够降低软、硬特性隔振系统幅频响应峰值，减小跳跃区间，提高系统的稳定性。

（2）增加库伦阻尼λ能够有效降低软特性隔振系统的幅频响应峰值，减小跳跃区域，提高系统稳定性；但库伦阻尼对硬特性隔振系统影响较为复杂：当λ≤0.5 时，库伦阻尼对系统的幅频响应及稳定性影响较小；当λ>0.5 时，幅频响应曲线会出现独立封闭环形区域，即出现“频率岛”，此时需要大幅提高库伦阻尼才能使“频率岛”消失，而且对减小不稳定区域的作用较小，因此，库伦阻尼更适合软特性隔振系统参数设计。

（3）微量增加几何非线性黏性阻尼η就能使软、硬特性隔振系统幅频响应峰值大幅降低，使硬特性隔振系统不稳定区域迅速减小，而且不会出现“频率岛”现象，但是几何非线性黏性阻尼对软特性隔振系统不稳定区域的影响并不显著，因此，几何非线性黏性阻尼更适合硬特性隔振系统参数设计。

（4）通过对几何非线性黏性阻尼隔振系统进行避跳参数设计，得到了避跳边界。同时，对于硬特性隔振系统，当λ≤0.5 时，避跳边界上的非几何非线性黏性阻尼η与线性刚度ρ近似呈线性关系；当λ>0.5时，由于“频率岛”等复杂的幅频特性导致避跳参数变化规律十分复杂，因此，硬特性隔振系统最好在λ≤0.5 范围内进行避跳参数设计。对于软特性隔振系统，避跳边界上的非几何非线性黏性阻尼η与线性刚度ρ近似呈线性关系，并且随着λ增加η随之减小，增大了系统稳定区域，因此，适当增加库伦阻尼λ对软特性隔振系统避跳参数设计具有积极作用。

（5）通过定频振动试验验证了理论计算的准确性以及避跳设计方法的普适性，因此，上述计算得到的几何非线性隔振系统非线性动力学特性规律以及采用的避跳参数设计方法，对非线性隔振系统参数设计具有重要的指导作用。