匀速旋转刚环⁃内接柔性梁系统的共振分析

2022-02-15陈渊钊吴文军

振动工程学报 2022年6期

陈渊钊，吴文军

（广西科技大学机械与汽车工程学院工程力学系，广西柳州 545006）

引言

无轴轮缘驱动推进系统的主要结构是环形导管和无轴螺旋桨［1］，可通过转动环形导管，带动安装在导管内壁的叶片旋转，不需要使用轮毂，不存在“轴”。这种“无轴”特征使此类结构在减振降噪上有独特优势，对提高潜水艇的隐蔽性具有重要的应用价值。

由于螺旋桨具有较大的细长比，环形导管-螺旋桨可简化为旋转刚环-柔性梁系统进行研究，其实质是一类刚-柔耦合动力学系统，这类系统广泛应用的建模方法是柔性多体系统动力学中的浮动坐标系法。该方法利用浮动坐标系来描述构件的弹性变形，并认为构件的位形是浮动坐标系的大范围运动与弹性变形的叠加，由此来表达大范围运动和弹性变形之间的耦合关系。在耦合关系中还需要考虑梁弯曲导致的轴向缩短量。根据计算耦合缩短量不同的程度，浮动坐标系法可建立零次刚柔耦合动力学模型［2］、一次刚柔耦合动力学模型［3-5］和高次刚柔耦合动力学模型［6］。

浮动坐标系法常用于研究中心刚体-柔性梁系统动力学与控制问题。文献［7-11］将一次近似耦合模型应用于旋转梁、旋转板的自由振动分析，详细讨论了转速、集中质量、复合材料的相关参数、横向和轴向变形之间的耦合等因素对结构振动特性的影响，并指出这类系统随着角速度的增大会产生频率迹线转向和振型转换现象。和兴锁等［12］通过进一步计入轴向变形对横向变形的影响，提出了一种更完备的柔性梁一次近似耦合模型。Li 等［13-14］和吴根勇等［15］分别将一次近似耦合模型应用于研究旋转功能梯度梁（板）和复合材料板的自由振动问题。方建士等［16-17］讨论了横向和轴向变形之间的耦合对旋转柔性梁频率迹线转向的影响，并引入了尺度效应进行研究。高晨彤等［18］建立了旋转功能梯度梁基于倾角坐标的一次刚柔耦合模型，并考虑剪切变形的影响，分析了楔形比和材料梯度分布规律对频率特性的影响。范纪华等［19］研究了温度作用下的旋转功能梯度梁的动力学响应。为满足任意形状梁结构的离散需求，范纪华等［19-21］和杜超凡等［22-23］分别采用计算几何方法和无网格法离散旋转柔性梁，并获得了良好的数值结果。文献［24-25］建立了带集中质量的功能梯度梁的高次耦合模型，并对该结构在温度场中的自由振动和振动控制展开了深入研究。

上述的中心刚体-柔性梁系统，其“柔性梁”是外接于中心刚体上，离心力属于“拉力”。与之不同，无轴轮缘驱动推进系统的“柔性梁”内接于“刚环”内壁，离心力属于“压力”，在“压力”较大时，压杆易出现失稳现象。因此，旋转刚环-柔性梁系统的研究更为关注梁结构的屈曲和稳定性。Mostaghel 等［26］基于结构力学建立了旋转内接柔性梁（板）的离心力与变形之间的关系，给出了径长比与临界失稳转速的关系式。Wang［27］研究了旋转内接柔性梁的安装角对临界失稳转速的影响。William 等［28］讨论了旋转平面内屈曲和平面外屈曲的临界失稳转速。Yu等［29］结合伽辽金法和牛顿线性化方法，给出了匀速旋转环-内悬臂梁系统振动的解析解。方建士等［30］建立了内悬臂梁系统的一次刚柔耦合动力学模型，分析了系统在不同转速和径长比参数下的稳定性。

值得注意的是，在系统匀速旋转时重力与梁之间的夹角产生周期性的变化，从而使得重力周期性地激励内悬臂梁。若旋转角速度令重力激励的频率接近系统的固有频率，则会产生共振问题，易使结构产生破坏。然而，目前关于旋转刚环-柔性梁系统共振转速的研究鲜有报道。

本文基于浮动坐标系法，结合梁由于弯曲而产生的轴向缩短量，采用有限元法建立旋转内接柔性梁的一次刚柔耦合动力学模型，以此来研究旋转内接柔性梁的共振转速区间和动力学行为，以期为无轴螺旋桨结构动力学设计提供参考数据。

1 内接柔性梁动力学建模

本文将环形导管和无轴螺旋桨简化为刚环-悬臂梁系统，如图1（a）所示。刚环-内接悬臂梁始终在竖直平面上绕圆心做旋转运动，刚环角速度为Ω，半径为R，在圆心O建立惯性坐标系O⁃XY和浮动坐标系O⁃X1Y1，两坐标系的夹角为θ，如图1（a）所示。其中，浮动坐标系O⁃X1Y1固联在悬臂梁上，用以描述悬臂梁的变形位移。鉴于无轴螺旋桨一般在铅垂面上运动，因此本文仅讨论刚环-悬臂梁系统的平面运动，采用平面Euler-Bermoulli 梁模型进行研究。如图1（b）所示，梁上任意一点P的横向变形为w。

图1 刚环-柔性梁系统及变形Fig.1 System and deformation of steel ring-flexible beam

如图2所示，沿梁中轴线的微元M0N0，其端点在浮动坐标系上的坐标分别为M0（ξ，0）和N0（ξ+dξ，0）。微元变形后记为MN，其长度为：

图2 梁的变形位移描述Fig.2 Description of deformation displacement of beam

式中下标“，ξ”表示对弧长坐标ξ求一次导数。

将式（1）进行泰勒展开，鉴于轴向变形远远小于横向变形，忽略w，ξ的三次以上高阶项，忽略u0，ξ的两次以上高阶项，有：

对式（2）积分可得到变形后的梁长度为：

式中v为梁的实际轴向变形量，表示为：

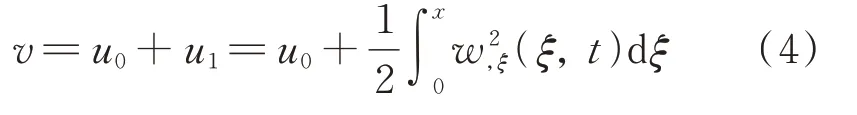
其中，u0主要由梁的伸缩产生，在刚环-悬臂梁系统中，梁所能产生的伸缩非常小，可忽略不计。u1为弯曲产生的轴向变形：

柔性梁的应变能为：

式中E和I分别为柔性梁的弹性模量和截面惯性矩；L为梁的长度。

此外，柔性梁做旋转运动，在小变形情况下，可认为其离心惯性力作用于中轴线上。根据式（5），横向变形势必会引起轴向长度的缩短。这样的缩短使离心力沿着轴向产生了移动，从而使整个系统需要考虑离心力对系统做的功。梁上的某个微元的离心力可表示为：

式中ρ和A分别为梁的质量密度和横截面积。

离心力做的功可表示为：

系统在旋转时，梁所受重力会产生周期性变化。梁上微元的重力可表示为：

这里假定初始时刻惯性坐标系O⁃XY和坐标系O⁃X1Y1重合。梁重力做的虚功可表示为：

梁上任意一点P的速度可表示为：

式中Ω为刚环-悬臂梁系统的转动角速度。

这样可得到系统的动能为：

采用有限元法来离散柔性梁，梁上任意一点的变形可表示为：

其中

式中l为梁单元长度；下标“，x”表示对弧长坐标x求一次导数，下标i表示单元结点的编号。

可推导得到旋转内接柔性梁的动力学方程：

其中

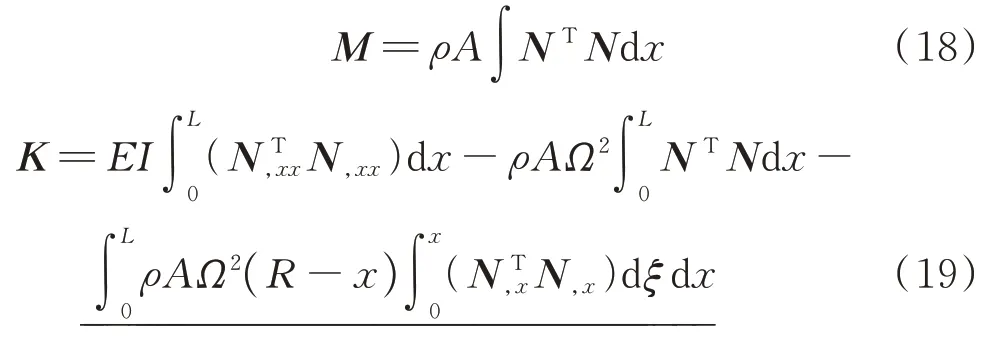
式中F1和Fg分别为离心广义力和重力广义力。

由于离心力广义力和弹性广义力可以表达成一项，因此动力学方程（17）中未直接看到离心力广义力，而是体现在刚度阵（19）的单下划线项中。

2 旋转内接柔性梁的模态特性

若记q=z，并忽略重力的影响，动力学方程改写为：

方程的解可表示为z=Zejωt，可推导得到系统的频率特征方程：

式中ω为圆频率。

表1给出了刚环-柔性梁系统的参数，根据这些参数，可计算得到梁的频率和模态。为更好地与文献［26］数据进行对比，引入无量纲参数：

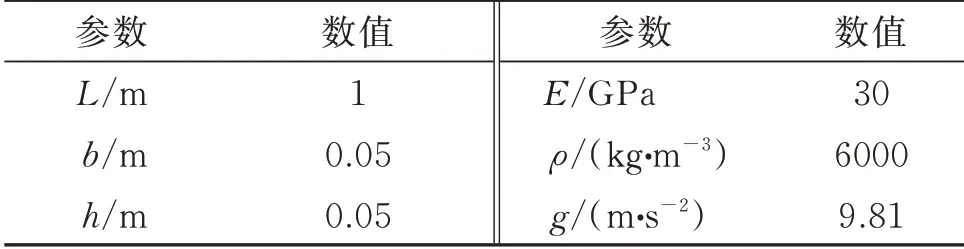
表1 刚环⁃柔性梁系统的参数Tab.1 Parameters of system of steel ring⁃flexible beam

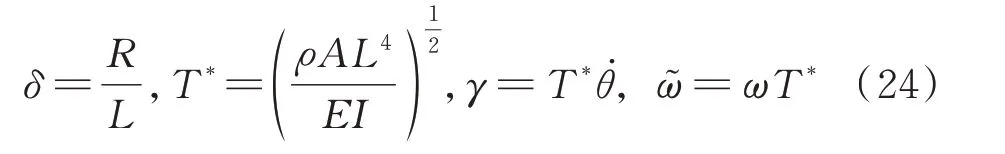
式中δ，γ和分别为系统的径长比、无量纲转速和无量纲频率。

表2给出了柔性梁在无量纲转速分别为0，1，2，3 时的前两阶无量纲频率，对应的径长比δ=1。可以看出，在这四个转速下，本文模型分别采用5，10，20 个单元计算，ANSYS 采用100 个beam188 单元，两种方法计算得到的无量纲频率几乎完全吻合，可验证本文所建立的内接悬臂梁动力学模型的正确性，也说明本文所采用的梁单元具有优良的收敛性。此外，注意到在无量纲转速为3 时，两种方法得到的第一阶无量纲频率均等于0。当频率等于0 时，意味着结构处于失稳状态，也就是说，在无量纲转速为3时，内接旋转悬臂梁会产生失稳。

表2 不同转速下的固有频率（δ=1）Tab.2 Natural frequencies at different speeds（δ=1）

图3给出前两阶无量纲频率随无量纲转速变化规律，对应的径长比仍为δ=1。可以看出，无论是第一阶还是第二阶无量纲频率，均随着无量纲转速的增大而逐渐减小。如第一阶无量纲频率在无量纲转速为零时约为3.5，然后随着无量纲转速的增大开始减小，在无量纲转速为3 时，第一阶无量纲频率刚好等于0，达到了失稳的临界值，因此无量纲转速为3 时正好是内接旋转悬臂梁的失稳临界转速。类似地，第二阶无量纲频率在无量纲转速约为12.2 时等于0，但比第一阶无量纲频率的失稳临界无量纲转速大得多，在无量纲转速未达到12.2 但大于3 时，梁已经失稳。因此，本文仅讨论第一阶无量纲频率所对应的临界失稳无量纲转速以及共振无量纲转速。

图3 前两阶无量纲频率Fig.3 Dimensionless frequencies of the first two orders

图3仅分析了径长比δ=1 时的临界无量纲转速，而径长比对临界无量纲转速有较大影响。图4比较了径长比为1，2，3，4 时的第一阶无量纲频率随无量纲转速的变化曲线。不难发现，径长比为1 时的临界无量纲转速约为3；径长比为2 时的临界无量纲转速约为2.1；径长比为3 时的临界无量纲转速约为1.6；径长比为4 时的临界无量纲转速约为1.45。可以总结出这样一个规律：径长比越大，第一阶无量纲频率随无量纲转速增加而减小的幅度越大，减小至0（失稳）的“速度”也越快，对应的失稳临界转速也就越小。这是因为径长比越大、无量纲转速越大，柔性梁的离心力也就越大，柔性梁受压的程度也就越强，对应的频率就下降得越快。

图4 不同径长比的频率变化曲线Fig.4 Variation curves of the frequencies with different δ

图5给出了临界失稳无量纲转速随径长比的变化曲线。在文献［26］也给出了径长比与临界失稳转速之间的关系式，为γ2=72/（9δ−1）。可以看到，本文的计算结果与文献［26］所给出的关系式结果基本吻合，仅在径长比小于0.3 以后略有差异，造成这样细微差异的主要原因可能是本文与文献［26］在动力学建模方法上存在差异，但数值结果整体上基本一致，可说明本文模型的正确性。

图5 临界失稳转速随径长比的变化曲线Fig.5 Variation curves of critical instability speed with δ

目前，关于旋转内接悬臂梁的研究大多集中在分析其失稳临界转速上，但事实上，内接旋转悬臂梁还可能面临共振问题。如图6所示，无量纲转速对应的频率直线=γ从0 开始增大；而梁的第一阶无量纲频率均从3.5 开始减小。因此，直线与第一阶无量纲频率曲线必定会有交点，而这个交点代表着无量纲转速等于第一阶无量纲频率，意味着转动很可能会发生共振现象。那么，在这个共振点所对应的无量纲转速，可称之为共振转速。可以看出，不同的径长比有不同的共振转速：径长比为1 的系统，交叉点为γ=2.27；径长比为2 的系统，交叉点为γ=1.77；径长比为3 的系统，交叉点为γ=1.50；径长比为4 的系统，交叉点为γ=1.32。从图6中也容易看出，共振转速显然比失稳转速要小得多。

图6 共振转速Fig.6 Resonance speed

图7给出了共振转速随径长比的变化曲线。不难发现，径长比越大，共振转速就越低。此外，此共振转速曲线通过曲线拟合，得到以下经验公式：

图7 共振转速随径长比的变化曲线Fig.7 Variation curves of resonance speed with δ

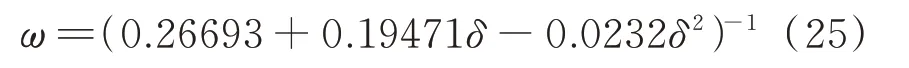
经验公式与数值结果吻合度较好，可直接用于相关结构共振转速的测算。

3 旋转内接柔性梁的受迫振动

图8给出了在无量纲转速分别为2.1775，2.2775，2.3775，3 下的梁末端变形，梁的径长比为1，对应的实际转动角速度分别约为70.04，73.5，76.49和96.82 rad/s。此时梁的共振无量纲转速和失稳无量纲转速分别为2.2775 和3。

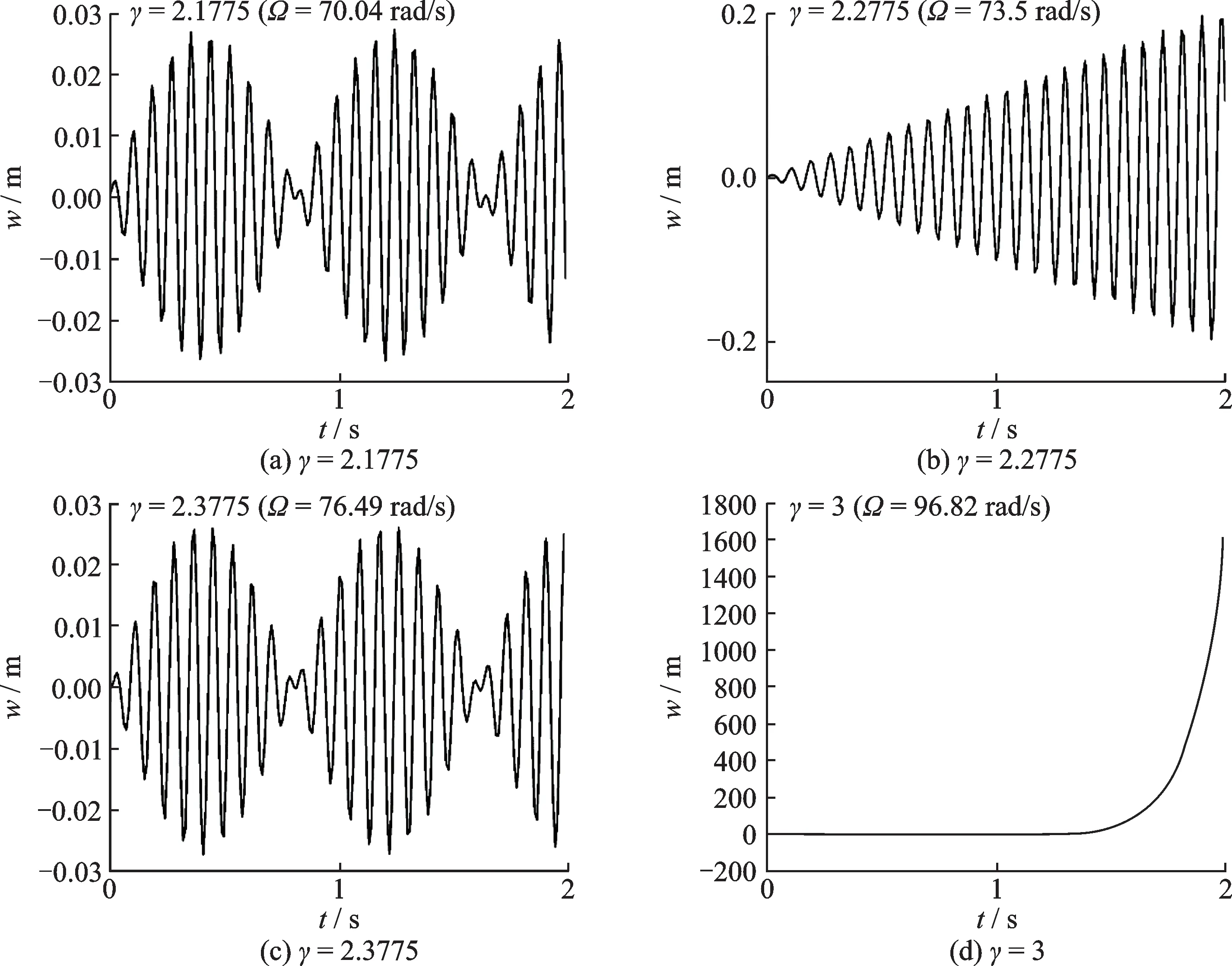
图8 不同转速下的动力学响应Fig.8 Dynamic responses with different speeds

在无量纲转速与共振无量纲转速比较接近时，如图8（a）和（c）所示，无量纲转速分别略小于和略大于共振转速（γ=2.1775 和2.2775），梁振动的振幅时而变大，时而变小，产生拍振现象。这是因为此时梁的动力学响应是梁自由振动和受迫振动的叠加，而在梁自由振动的固有频率和受迫振动的激励频率相差不大的情况下，即可出现拍振。换句话说，在产生拍振的转速附近，可能存在共振转速。

在无量纲转速等于共振转速时（γ=2.2775），如图8（b）所示，梁末端变形的振幅随着时间的增大而逐渐增大。图9是对应的相图，可看到变形不断增大、变形的速度也不停地增加，出现剧烈的振荡，即产生了共振现象；在无量纲转速等于失稳转速时（γ=3），如图8（d）所示，梁的末端变形随时间迅速增大，产生失稳现象。

图9 共振时的相图Fig.9 Time phase diagram under resonance

若将图8（b）的数据结果进行傅里叶变换，并归一化，可得到图10所示的位移幅频曲线。可以看到，位移幅频曲线的峰值出现在2.25，在共振转速2.27 附近。可将振幅下降至其峰值的1/ 2 倍时所对应的频段定义为共振区，那么此时系统的共振区为2.20 至2.36，即图10中的红色区域。根据图8的分析，系统的转速应当避开共振区转速，并小于失稳转速，否则系统将会出现位移共振或者失稳现象。因此，γ<2.20 和2.36<γ<3 是刚环-柔性梁系统可正常工作的转速区间。