π型加劲梁软颤振特性及下稳定板的影响研究

董国朝，许育升，韩 艳，李 凯，蔡春声，2

（1.长沙理工大学桥梁工程安全控制教育部重点实验室，湖南 长沙 410114；2.路易斯安那州立大学，路易斯安那州 巴吞鲁日 LA70803）

引 言

开口断面主梁因具有良好的受力性能、吊装简便和造价低等优点，常用于大跨度斜拉桥和悬索桥，如鄂东长江大桥、荆岳长江大桥、鹦鹉洲长江大桥和宜昌庙嘴长江大桥等。其主要断面类型有主肋混凝土板梁、π 型钢-混凝土叠合梁及半封闭式钢箱梁等。相对于线性颤振［1-3］，由于主梁的气动非线性和结构非线性，一些学者［4-7］在大振幅下观察到部分桥梁断面存在极限环振荡（Limit Cycle Oscillation，LCO）现象，表现为当风速超过某个“临界点”后，结构的振动响应不会立刻发散，其振幅在某一风速下保持稳定并随风速的增大而增大。为区别硬颤振，国内外学者称其为“软颤振”（Soft Flutter）。

事实上，早期研究发现旧Tacoma 桥在风毁前大约经历了70 min 的扭转振动，振幅为30°～35°，这一发现表明真实的颤振响应并非完全与线性颤振理论预测的结果一样。许多学者通过风洞试验也发现，由于空气动力学或结构的非线性，部分桥梁断面可能存在极限环振荡现象。Amandolese 等［8］和Pigolotti 等［9］研究了薄板的后临界颤振行为，发现其存在显著的竖弯-扭转耦合的LCO。Gao 等［10］通过风洞试验发现了双侧悬挑箱梁表现出显著的后临界LCO，且具有轻微的弯扭耦合效应。伍波等［11］基于武汉杨泗港长江大桥风洞试验，对比了不同动力参数下桁架梁的软颤振特性。许福友等［12］对印尼Suramadu 大桥进行了风洞试验研究，发现钝体主梁断面的软颤振特性，得出颤振形态与断面形式、模态频率和质量相对比例有关。

部分学者在π 型加劲梁断面也观察到了软颤振现象［13-17］。Kubo 等［14］在两个（板梁位置不同）π 截面上发现了其非线性颤振性能。董佳慧等［15］发现了边箱钢-混叠合梁π 型断面的软颤振表现为振动频率单一且以扭转为主的弯扭耦合运动。方根深等［16］通过风洞试验发现，π 型梁断面存在软颤振现象且风攻角效应明显。此外，由于其气动外形较钝，对风的敏感性较强，在不进行气动优化情况下，易出现明显的颤振现象［18-22］。试验和实际工程中常采用气动措施进行优化，其中，下稳定板是用于改善开口断面主梁气动稳定性的有效气动措施之一。郑史雄等［18］分析了不同角度的风嘴及稳定板对π 型加劲梁断面的软颤振的抑制效果，发现下中央稳定板对软颤振作用效果不明显。Irwin［19］介绍了底部隔板对开口断面主梁的气动抑制效果。杨光辉等［20］和战庆亮等［21］结合风洞试验和计算流体力学（Computational Fluid Dynamics，CFD）发现下稳定板能改善π 型开口断面主梁的气动稳定性。杨詠昕等［22］发现中央稳定板能显著提高三类主梁的颤振稳定性能且控制效果与稳定板的位置和高度有关。以上研究结果大部分是基于风洞试验分析π 型加劲梁设计断面软颤振特性，有关数值模拟及气动优化措施对软颤振的影响报道较少。因此，借助可视化的计算流体动力学方法，深入研究π 型加劲梁悬索桥的软颤振特性及下稳定板的影响机理具有重要意义。

本文基于数值模拟方法并结合风洞试验，以某π 型钢-混凝土结合梁大跨悬索桥为研究背景，通过对比风洞试验三分力系数验证网格和时间步长的无关性，对比颤振临界风速结果验证数值模拟方法的可靠性，并进一步通过数值模拟结果分析加劲梁的软颤振特性及1/4 下稳定板对π 型加劲梁软颤振的影响，探讨π 型加劲梁的软颤振机理及1/4 下稳定板对其影响机理。

1 风洞试验概况

某加劲梁断面形式为开口钢-混凝土结合梁的大跨悬索桥［23］，主跨为838 m，桥型布置如图1所示。加劲梁宽33.2 m，高2.8 m，加劲梁断面及优化措施即下稳定板的位置如图2所示，1/4 下稳定板（即桥梁横断面开口宽度（1/4）L处，且下稳定板的下缘与检修轨道底部平齐）在节段模型中的布置如图3所示。对主梁进行节段模型颤振试验，试验风速比为1∶3.4，模型缩尺比为1∶50，试验主要动力特性参数如表1所示。

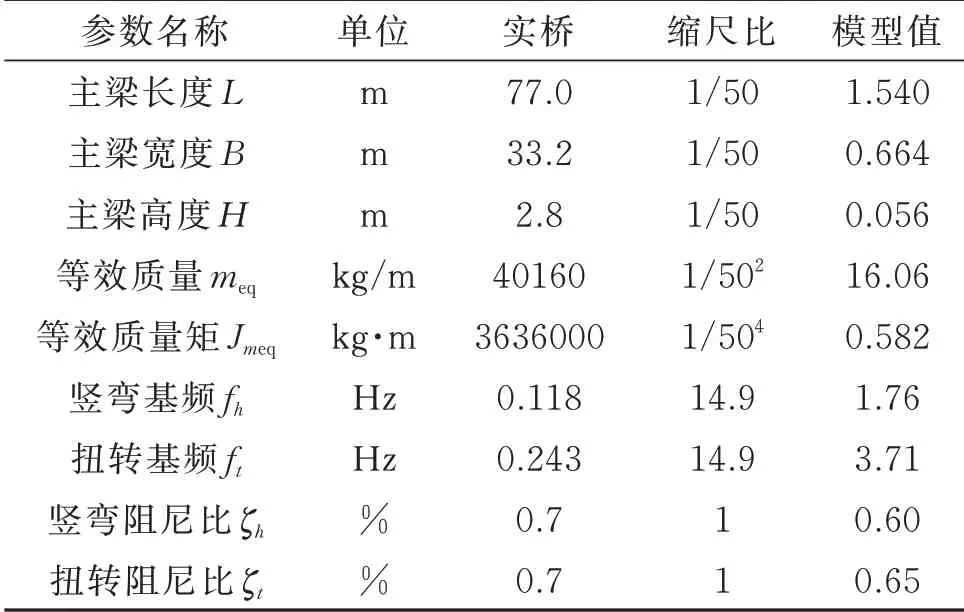
表1 动力特性参数表Tab.1 Dynamic characteristic parameter table

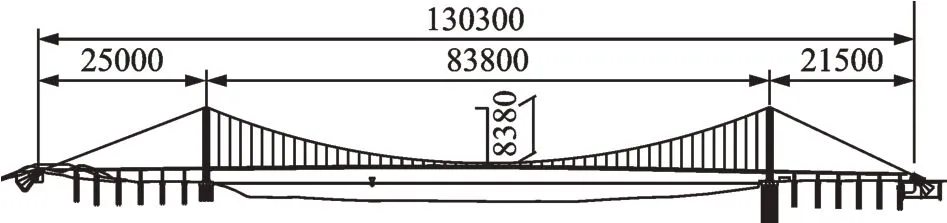
图1 桥型布置图（单位：cm）Fig.1 Layout of the bridge（Unit：cm）

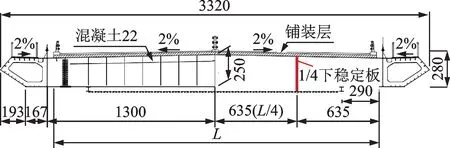
图2 加劲梁断面及气动措施位置示意图（单位：cm）Fig.2 Cross section of stiffening beam and location of aerodynamic measures（Unit：cm）

图3 节段模型1/4 下稳定板布置图Fig.3 1/4 lower stabilizers layout of the segmental model

原设计加劲梁断面的颤振试验结果［23］表明：+3°攻角下，原设计断面的颤振临界风速为31 m/s，低于颤振检验风速，不满足抗风要求［24］。采取多种气动优化措施进行节段模型颤振试验后，发现在原设计加劲梁断面下表面增设1/4 下稳定板的气动措施对加劲梁的颤振临界风速提高效果最明显。此外，文献［14-17］的研究结果表明π 型加劲梁断面及优化方案（增设1/4 下稳定板）存在一定的软颤振现象。为了进一步探明π 型加劲梁的软颤振特性及下稳定板对其的影响机理，建立二维两自由度（扭转和竖弯）的数值模型进行计算，并借助CFD 可视化流场进一步分析。

2 数值模拟

2.1 网格及时间步长无关验证

Gao 等［10］和董佳慧等［15］在研究桥梁的软颤振试验时，发现桥面的附属结构会增加软颤振响应，减小软颤振的振幅增长速率，而且栏杆等附属结构能进一步增强来流在桥断面附近的分离，增强自激力的非线性特性。建模时保留栏杆和下检修道等附属结构，以进一步准确模拟加劲梁断面附近的流场。数值模型的尺寸与风洞试验模型保持一致，网格计算域划分为“静网格域”、“刚性域”和“动网格域”。其中，刚性域内包括边界层以及相应的网格加密，并与加劲梁断面同步运动，目的是保证加劲梁断面周围具有较高的网格精度，以更好地捕捉旋涡的分离和再附。动网格域采用非结构化的三角形网格按一定疏密填充，外部静网格域采用结构化的四边形网格。湍流模型采用二维大涡模拟（Large Eddy Simulation-2D），速度压力耦合采用SIMPLEC 求解。计算域及近壁面网格如图4所示，网格阻塞率小于3%。

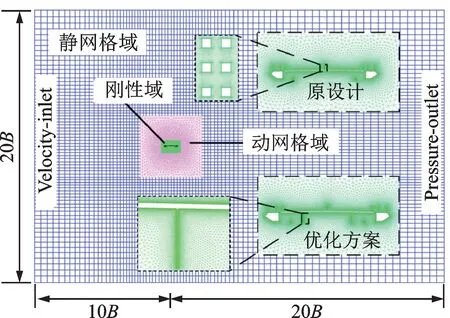
图4 网格及计算域Fig.4 Grid and computing domain

在保证计算准确的前提下，为提高计算效率，以原设计加劲梁断面为例，对网格和时间步长进行了无关性测试。采用三套增长疏密不同的网格（Case1，Case2 和Case3）及三种不同时间步长（T1=0.001 s，T2=0.0005 s 和T3=0.0001 s）进行测试，网格参数如表2所示。风洞试验中，桥梁主要发生扭转自由度的颤振现象，因此，以原设计加劲梁断面0°攻角的阻力系数和扭矩系数结果为参考值来验证网格及时间步长的无关性。三分力系数定义如下：

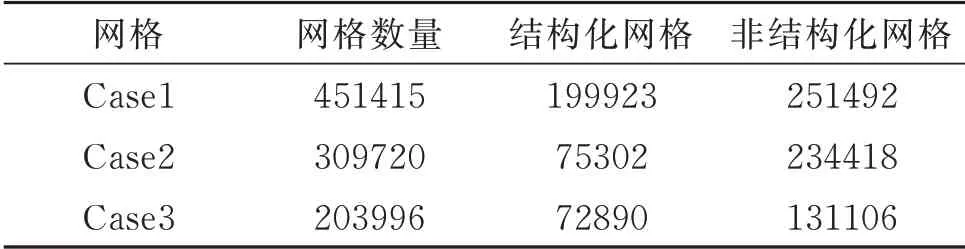
表2 网格参数Tab.2 Parameters of grid

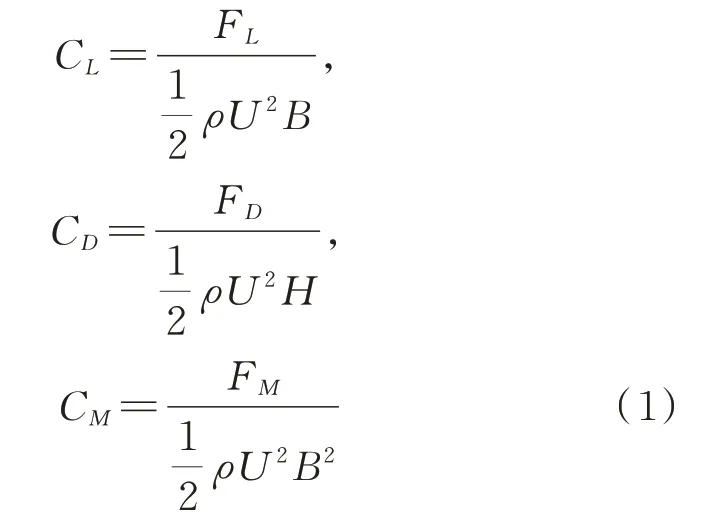
式中CD为阻力系数；CL为升力系数；CM为扭转系数；FD，FL和FM分别代表桥梁断面受到的阻力、升力和扭矩。模型宽度B=0.664 m；模型高度H=0.056 m；U为来流风速；空气密度ρ=1.225 kg/cm3。

0°攻角下，来流风速U=10 m/s 时，原设计断面的风洞试验与数值模拟的三分力系数结果对比如表3所示。网格及时间无关性测试结果表明：Case1，Case2 和Case3 的网格在0.001，0.0005 及0.0001 s 的时间步长下三分力系数计算结果与风洞试验值吻合良好，表明网格的稳定性较好。兼顾计算精度和计算效率的前提下，选取时间步长为T1=0.001 s 以及数量为203996 的网格Case3 对各攻角下的颤振临界风速计算，进一步验证数值模拟方法的可靠性。为保证精确捕捉近壁面的旋涡的产生和脱落，要求YPlus具有足够的精度，网格近壁面YPlus值如图5所示，YPlus值整体小于1。

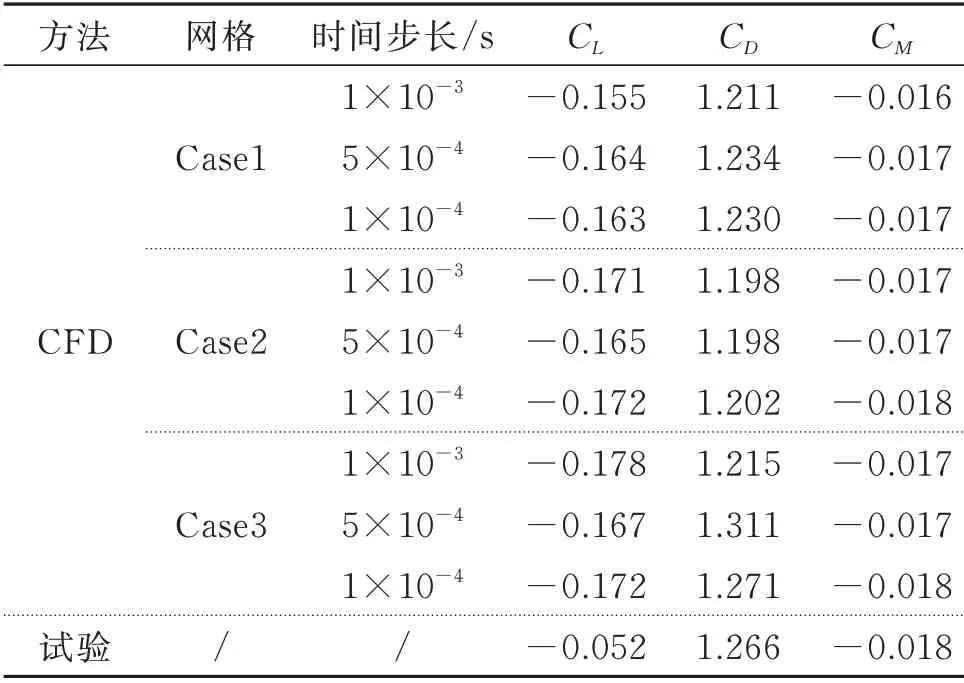
表3 网格及时间无关性验证结果Tab.3 Grid and time independent test results

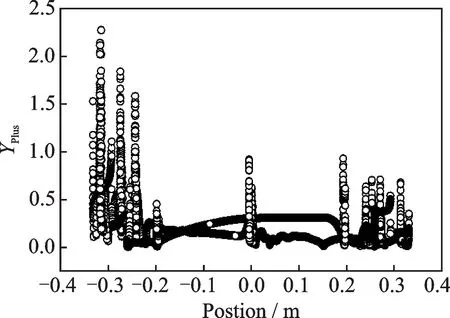
图5 近壁面网格YPlus值Fig.5 YPlus of the first layer mesh near wall

2.2 数值模拟方法可靠性验证

节段模型颤振试验结果表明原设计方案的颤振稳定性能较差，不满足规范要求，且气动优化方案（增设1/4 下稳定板）能显著提高加劲梁的颤振临界风速。为进一步验证数值模拟方法的可靠性，对各攻角下原设计加劲梁及优化方案的颤振临界风速进行计算。本文采用直接计算法［25］，借助Fluent 自带的动网格技术同时嵌入自编译的UDF 二次开发程序计算原加劲梁断面及优化方案在−3°，0°和+3°攻角下的颤振临界风速。网格重构方法使用Soomthing 和Remeshing 功能。根据抗风规范［24］：当颤振“发散点”不明显时，若扭转位移标准差达到0.5°，则认为发生颤振失稳。数值模拟与风洞试验的颤振临界风速对比结果如表4所示。

表4 原设计及优化方案的颤振临界风速结果Tab.4 Critical flutter wind speed of initial design and optimization scheme

风洞试验和数值模拟的颤振临界风速结果表明：数值模拟的原设计加劲梁断面及优化方案的颤振临界风速与风洞试验结果吻合较好，数值模拟的颤振临界风速值相比风洞试验的结果整体偏低，在原设计的+3°攻角上出现最大误差为5.7%。原设计断面+3°攻角相比0°攻角和−3°攻角的颤振稳定性较差，与文献［18，21］结果的趋势一致。且风洞试验和数值模拟的结果均表明1/4 下稳定板能显著改善加劲梁的颤振稳定性。颤振临界风速的对比结果验证了数值模拟方法的可靠性，因此，下文基于数值模拟结果对π 型加劲梁的软颤振特性及下稳定板的影响进一步研究。

3 软颤振分析

根据数值模拟和风洞试验结果，本文研究的加劲梁主要振动形式为扭转振动，且在原设计断面上增设1/4 下稳定板能有效降低加劲梁的颤振临界风速。数值模拟结果表明：当风速小于“临界点”时，加劲梁的扭转振动表现为随机的小振幅振动；当风速大于“临界点”时，加劲梁的扭转振动表现为振幅稳定的极限环振荡，如图6为设计加劲梁断面+3°攻角下风速为12 m/s 时的极限环振荡图。

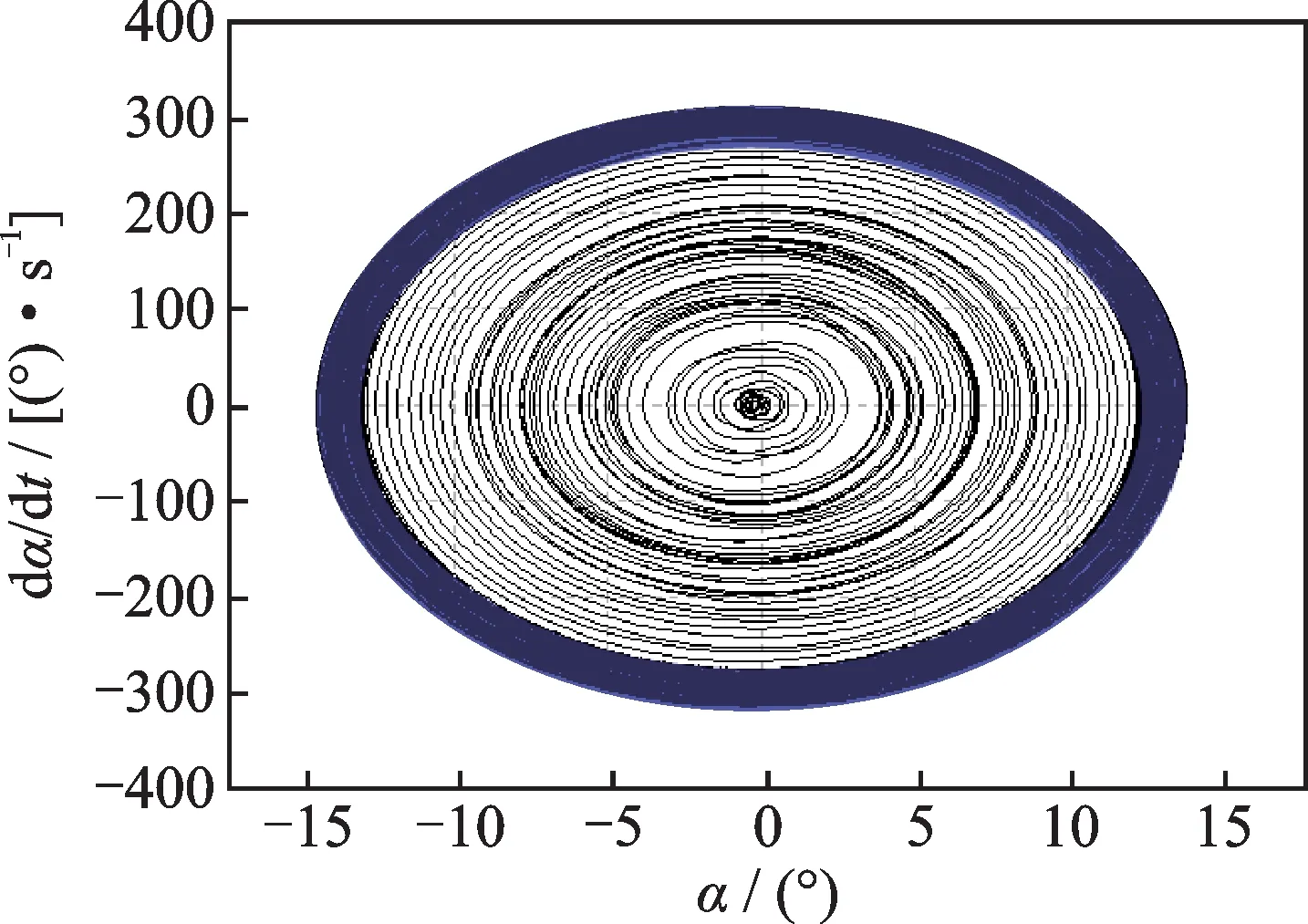
图6 极限环振荡（原设计断面+3°攻角，风速：12.0 m/s）Fig.6 Limit cycle oscillation（+3° attack angle of initial design，wind velocity：12.0 m/s）

图7为原设计及优化方案在各风攻角下的扭转角位移RMS 值随风速的变化，U=12 m/s 时原设计断面在+3°攻角下的扭转角位移时程曲线见局部放大图。原设计加劲梁断面及增设1/4 下稳定板的优化断面均出现了程度不一的软颤振现象，且存在明显的振幅“发散点”。在+3°攻角下，当风速达到12.0 m/s 时，原加劲梁出现明显的扭转振动，但未发散，振幅稳定在12°左右。加劲梁断面的稳定振幅随风速增大而增大，与涡激振动的振幅增长和振幅限制的现象相似。当风速大于振幅“发散点”时，加劲梁断面的振幅迅速发散，表现出与硬颤振类似的现象［1-3］，如0°攻角下原设计加劲梁断面风速达到16 m/s 时出现了发散性颤振。对比图7中各攻角的扭转位移随风速的变化，可以看出：正攻角的“发散点”风速较低，负攻角的“发散点”风速较高，且振幅的增长斜率随攻角减小呈减小趋势。负攻角的软颤振特性比正攻角的更加显著，这一趋势与文献［13，18］的结果一致。

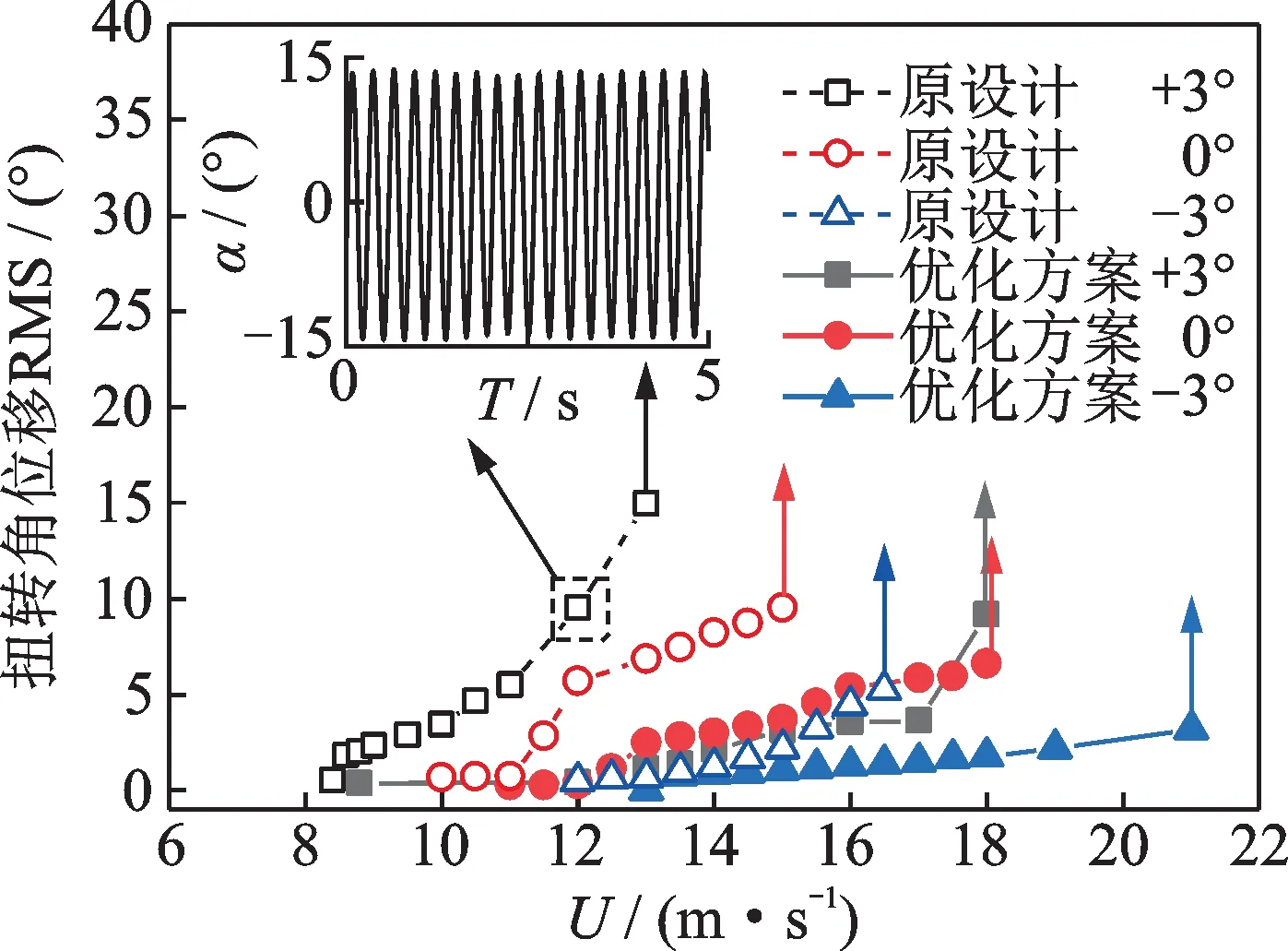
图7 扭转位移RMS 值随风速变化图Fig.7 Variation of RMS values of torsional displacement with wind speed

图7中，虚线和实线分别代表原设计加劲梁断面和优化断面的扭转位移RMS 值随风速变化曲线，可以明显看出，在原设计加劲梁断面上增设1/4 下稳定板有效地减缓了各个攻角的振幅增长斜率，降低软颤振的振幅，增大了原设计加劲梁断面各个攻角的起振风速和“发散点”的风速。1/4 下稳定板对正攻角的改善效果最明显。增设了1/4 下稳定板的优化断面的软颤振特性相比原设计加劲梁断面的更为明显。

由于原设计断面+3°攻角软颤振特性不明显，而0°攻角相对于−3°攻角的颤振临界风速更小，因此，限于文章篇幅，选择0°攻角对主梁的原设计方案和优化方案进行分析。图8给出0°攻角下原设计加劲梁断面的部分扭转角位移时程曲线。

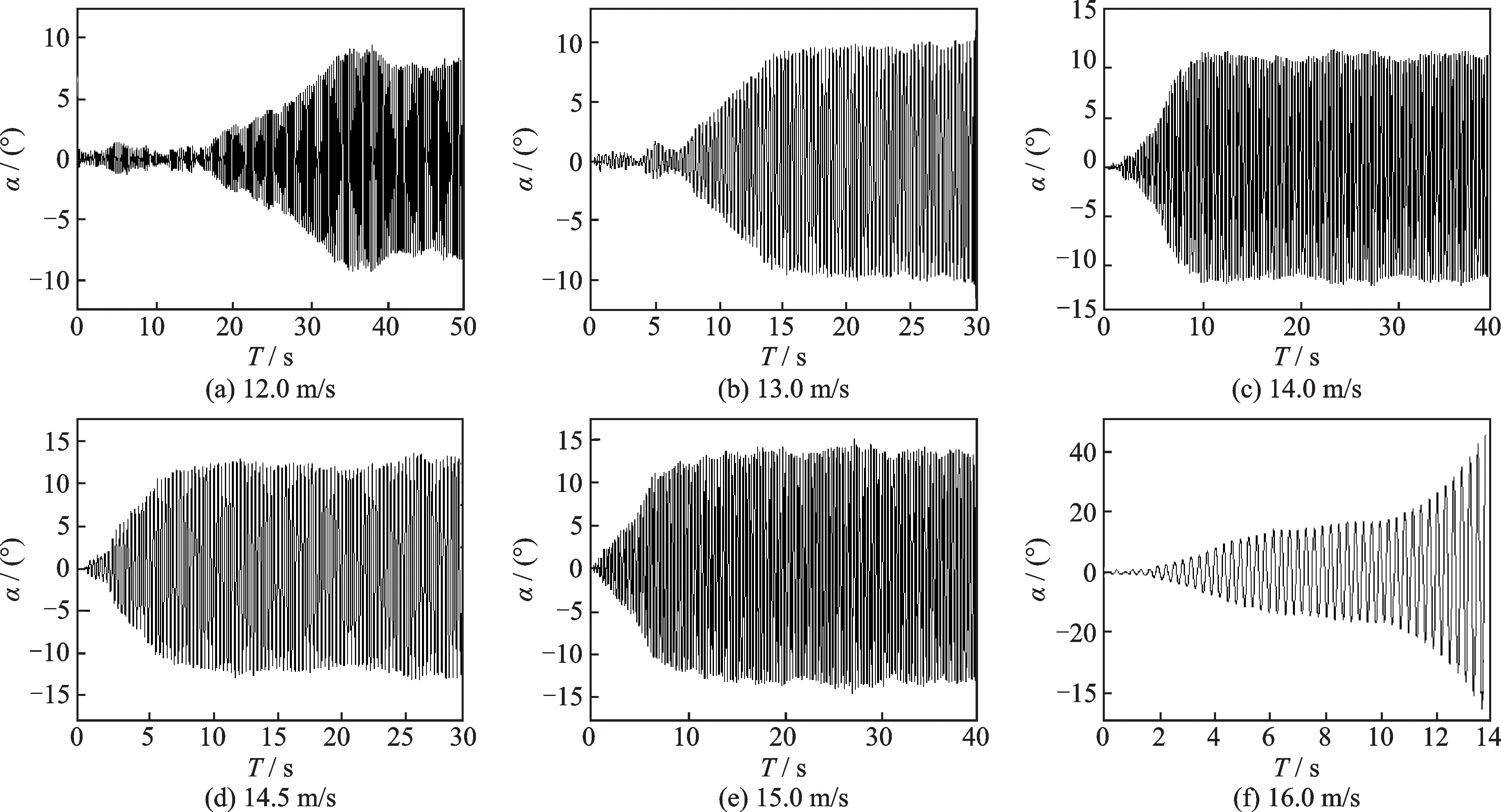
图8 原设计加劲梁断面位移时程（0°攻角）Fig.8 Displacement time history of initial design stiffening beam（0°attack angle）

图9为原设计加劲梁断面和优化方案在0°攻角下的振幅稳定时间（达到最大振幅所需的时间）随风速变化趋势图。风速为13.0 及16.0 m/s 时0°攻角下优化方案的位移时程曲线如图9中的小图所示。风速为13.0 m/s 对应的振幅稳定时间约为12 s；风速为16.0 m/s 达到最大振幅所需的时间约为7.2 s，振幅稳定时间随风速呈现递减趋势。风速小于14.0 m/s 时，增设1/4 下稳定板降低了原设计加劲梁断面的振幅稳定时间。当风速大于等于14.0 m/s时，增设1/4 下稳定板对原设计加劲梁断面的振幅稳定时间优化不明显。可以看出，增设1/4 下稳定板能减少原设计断面在低风速下达到振幅稳定所需的时间，对较高风速下振幅稳定时间的作用效果不明显。

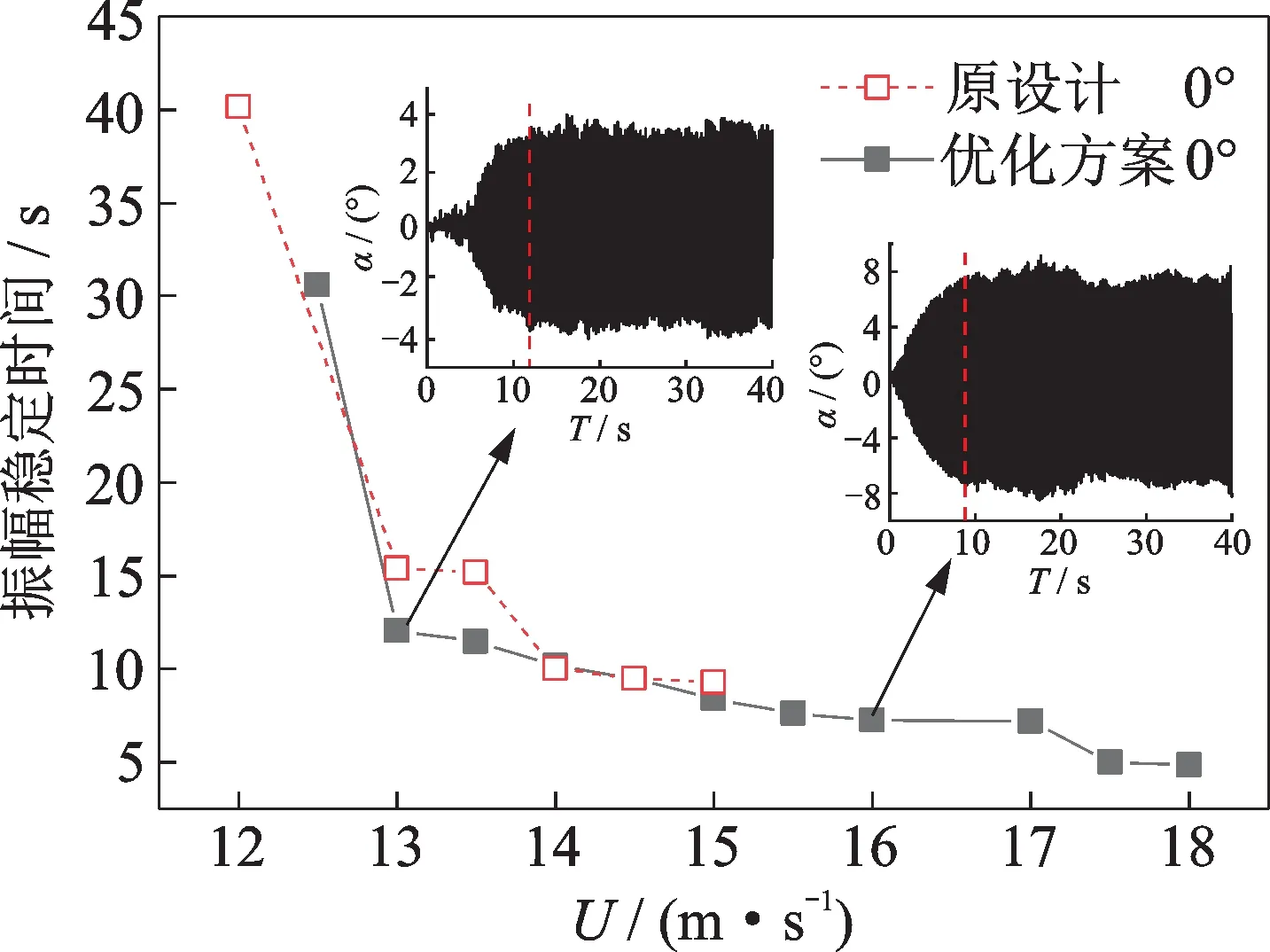
图9 振幅稳定时间随风速变化图Fig.9 Variation of amplitude stability time with wind speed

对各风速下的振动响应进行傅里叶变换，获得其频域特性。图10给出了原设计加劲梁断面和优化方案在0°攻角下的振动频率随风速变化的趋势图。原设计加劲梁断面和优化方案的振动频率减小斜率近似，振动频率随风速的增大均呈减小趋势。与文献［11］中桁架梁和文献［15］中π 型梁发生软颤振时颤振频率随风速增大而减小的特性相同。增设1/4下稳定板后，小幅降低了0°攻角各风速下原设计加劲梁的振动频率。图10中的小图给出了0°攻角下，原设计加劲梁断面在13 m/s时和优化断面在16 m/s时的频谱图。进一步对优化方案0°攻角下的竖向位移时程进行频谱分析，如图11所示。加劲梁的竖向振动的频率和扭转振动的频率一致，并与模型的第一阶扭转固有频率接近，这一现象与文献［16］一致。

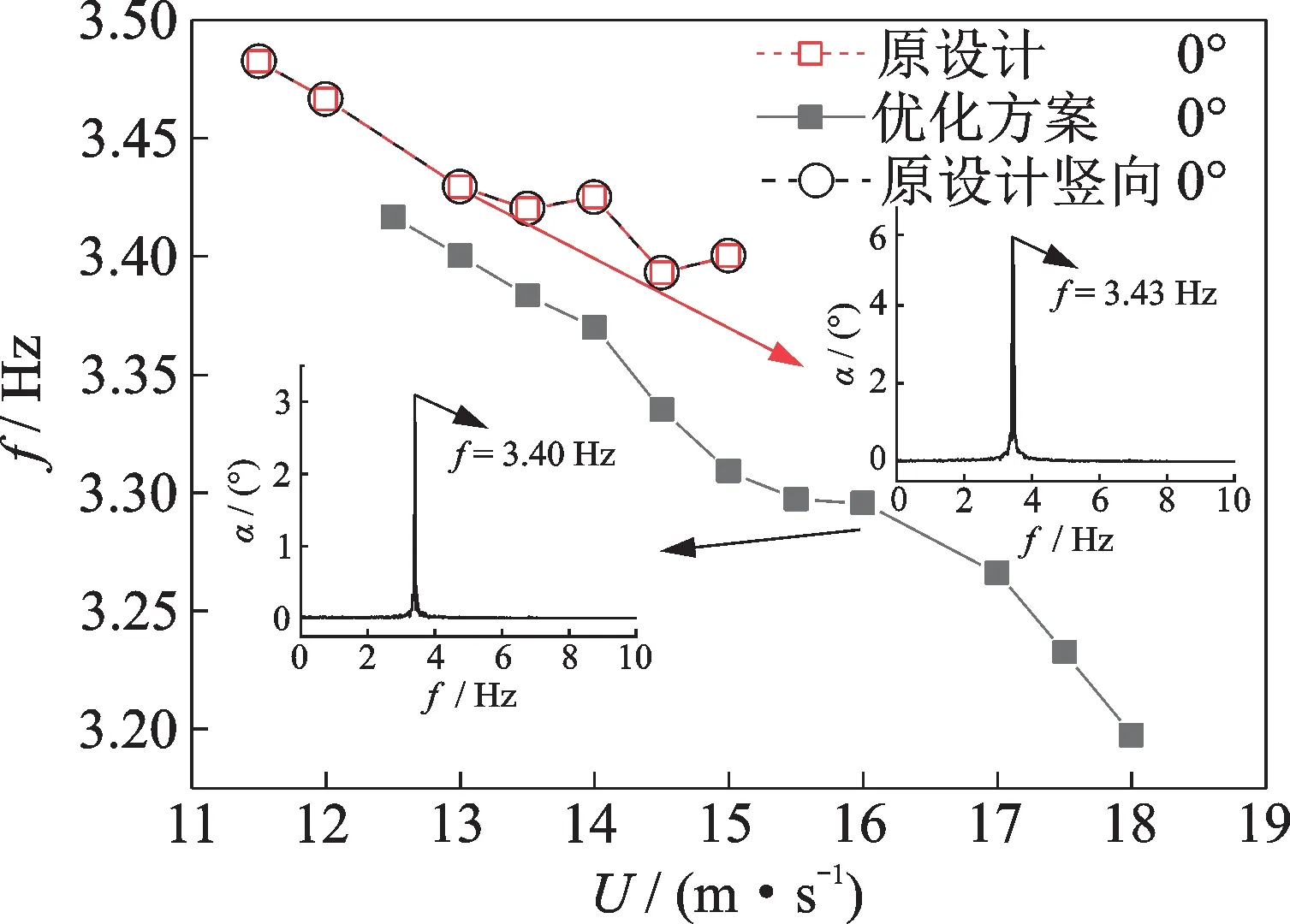
图10 频率随风速变化图Fig.10 Variation of frequency with wind speed

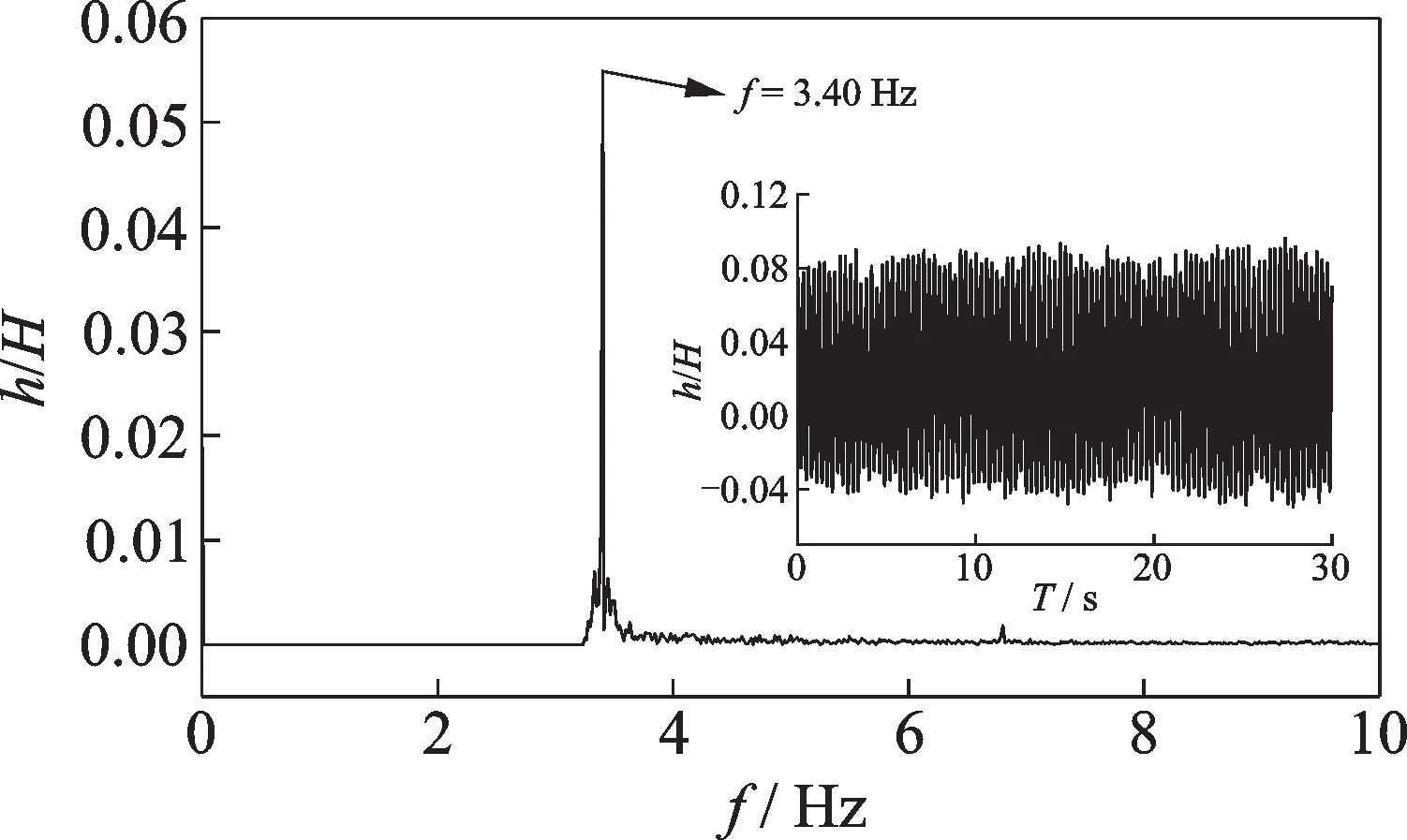
图11 优化方案0°攻角下竖向位移时程及频谱图（风速13.0 m/s）Fig.11 Time history and frequency spectrum of vertical displacement under 0° attack angle of optimization scheme（Wind velocity：13.0 m/s）

4 软颤振机理分析

4.1 振动系统能量分析

将自编译的UDF 二次开发程序导入Fluent，通过UDF 宏命令找到加劲梁断面的形心，对加劲梁断面壁面的压强积分计算得到每一个时间步长下加劲梁断面的升力矩M（t）。由于加劲梁的振动主要以扭转模态为主，因此，忽略竖向气动力的影响可以更清晰地分析π 型加劲梁断面软颤振过程中各能量的变化。加劲梁振动过程中系统的总能量Q、振动系统从外流场吸收的能量Qa和阻尼所消耗振动系统的能量Qc计算如下：

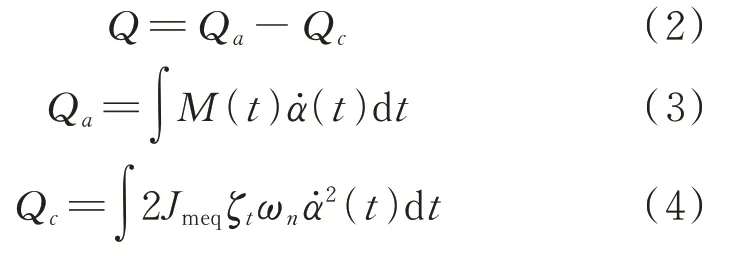
式中M(t)为力矩；(t)为角速度；Jmeq为模型等效质量矩，取0.582 kg⋅m；ζt为模型的扭转阻尼比取0.7%；ωn=2πft为扭转圆频率，取23.31 rad/s。

图12为原设计方案中0°攻角在风速为13.0 m/s下的系统的各能量随时间变化图。π 型加劲梁的软颤振振动过程可分为两个阶段：振幅扩散阶段和振幅稳定阶段。在振幅扩散阶段中，加劲梁的扭转位移由0 增大到最大稳定振幅。如图12所示，这一阶段中，振动系统从外流场吸收能量的速率明显大于阻尼消耗系统能量的速率，系统从外界吸收的能量大于阻尼消耗的能量，系统的能量增大，加劲梁的扭转位移增大。第二阶段为振幅稳定阶段，加劲梁的扭转振幅达到了最大稳定振幅，且振幅呈近似等幅。这一阶段中，振动系统从外界吸收能量的速率与阻尼消耗振动系统能量的速率相近，系统从外界吸收的能量近似等于阻尼所消耗的能量，系统的总能量值稳定在某一个值附近。

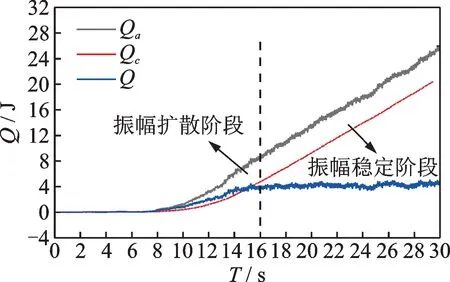
图12 振动系统各能量随时间变化图Fig.12 Component energy of vibration system varies with time

由0°攻角下原设计方案和优化方案在风速为13.0 m/s 的系统总能量可以发现：增设1/4 下稳定板后，系统总能量的稳定值降低了约86%，加劲梁达到最大扭转振幅所需的时间缩短。加劲梁的扭转振幅RMS 减小了63.7%，有效地改善了π 型加劲梁断面的颤振性能。为进一步分析风速对系统总功的影响，增加优化方案在0°攻角、风速17.5 m/s 时的工况，与优化方案在0°攻角、风速13.0 m/s 时的工况对比可以发现：虽然高风速下振幅扩散阶段的时间缩短了，但系统总功的增长速率明显大于低风速下系统总功的增长速率。因此，稳定阶段高风速下系统的总功大于低风速下系统的总功，高风速下扭转位移的最大稳定振幅大于低风速下的最大稳定振幅。图13中稳定阶段系统总功产生的较小波动是由于最大稳定振幅位移时程的波动造成的，与计算所采用的湍流模型有关。

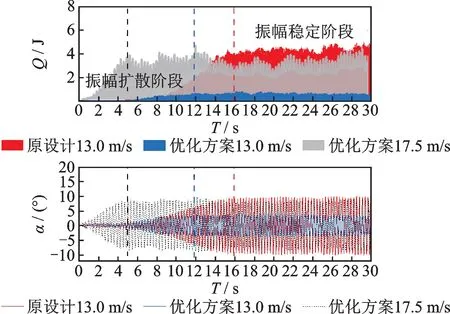
图13 振动系统总功及位移时程（0°攻角）Fig.13 Total work and displacement time history of vibration system（0°attack angle）

4.2 流场分析

分别取原设计π 型加劲梁及其优化方案在振幅扩散段及振幅稳定段的一个典型运动周期的流场进行分析，位移时程曲线如图14所示。着重分析T时刻（平衡位置）、T+T/4 时刻（最大扭转位移位置）、T+3T/4 时刻（平衡位置）和2T（最小扭转位移位置）时刻桥断面附近的流场演变过程。

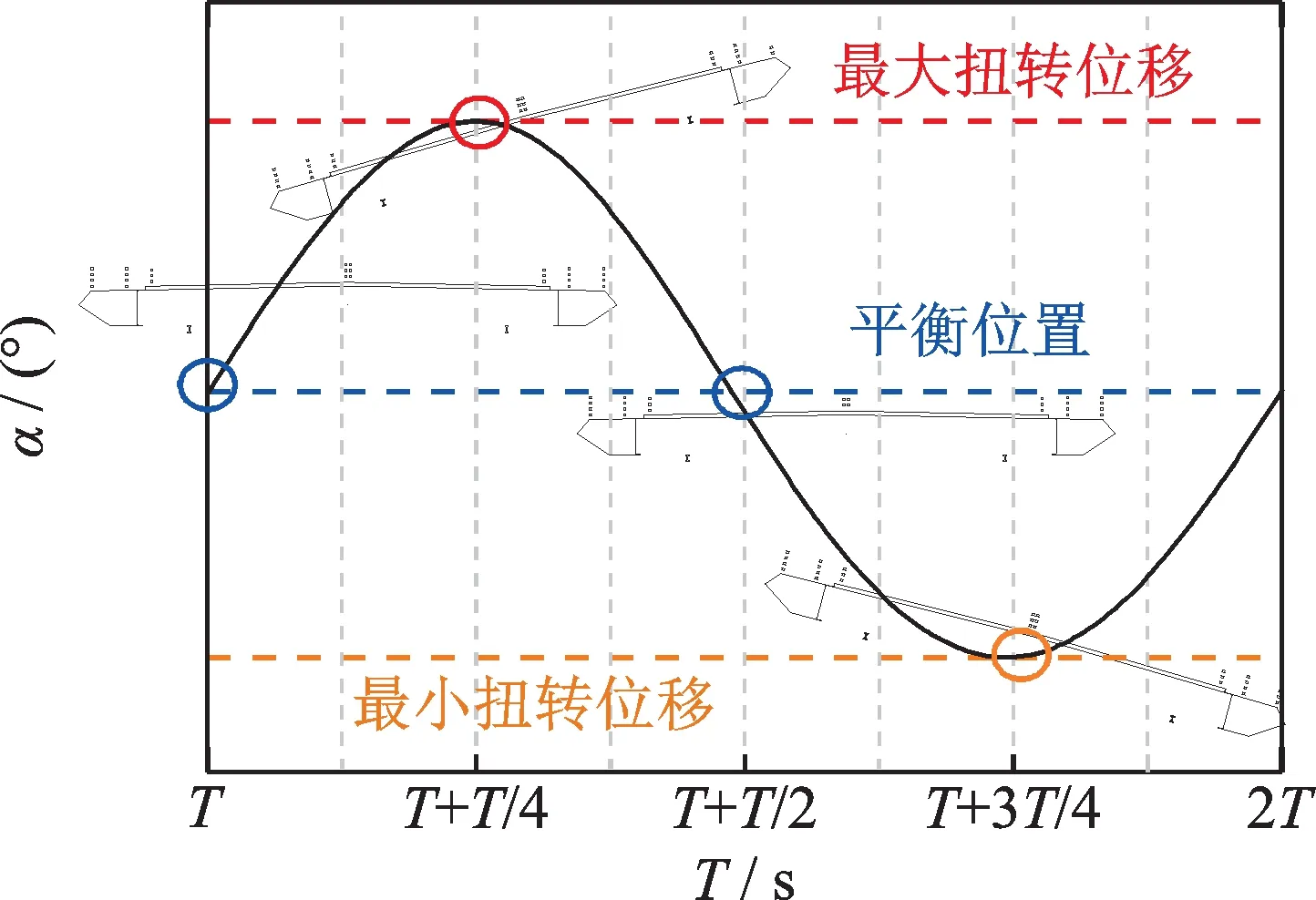
图14 典型周期位移时程图Fig.14 Displacement time history curve in typical period

0°攻角、风速为14.0 m/s 时原设计加劲梁断面在振幅稳定阶段典型周期的压力云图如图15所示。来流经原设计加劲梁断面，分别在上表面的上游栏杆处和上游箱室、下检修道处分离形成的旋涡脱落，并向下游发展，最终在尾部交替脱落。

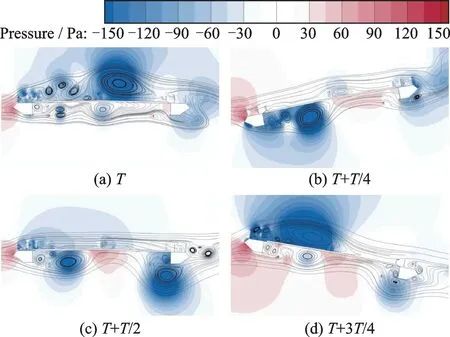
图15 原设计方案瞬时压力云图（0°攻角，风速14.0 m/s）Fig.15 Contours of static pressure of initial design（0° attack angle，wind velocity：14.0 m/s）

T时刻，上表面形成的旋涡运动至桥断面下游。下表面处，新的小涡在箱室及检修车轨道处产生并向下游发展。同时，上一周期的旋涡在下游箱室出现脱落，负压区逐渐远离桥面。下游下表面压力为正，上表面压力为负，气动力的方向在下游方向为竖直向上。此时桥梁断面处于平衡位置，气动力矩方向为逆时针，与桥断面的运动方向相同，气动力做正功，系统能量增大，促进振动发散。T+T/4 时刻，上表面的负压区较少，少量旋涡开始在栏杆处形成。下表面的旋涡在中间靠近上游处融合，形成一个较大的负压区，气动的方向竖直向下。此时，气动力矩减小，方向为逆时针，与桥梁的运动方向相同，气动力做正功，促进扭转振动的发散，桥梁断面达到最大扭转位移位置。T+T/2 时刻，下表面的主涡继续发展，旋涡的尺度增大并在下游箱室尾部开始脱落，气动力在下游方向为竖直向下。同时，新的旋涡开始产生并在下表面中间靠近上游处盘旋，旋涡的尺度较小。此时，桥梁断面处于平衡位置，气动力矩方向为顺时针，与桥梁断面的运动方向相同，系统能量增大，促进了振动发散。T+3T/4 时刻，上表面小的旋涡在上游融合形成了一个尺度较大的旋涡，生成了较大的负压区，气动力的方向在桥断面上游方向为竖直向上。下表面旋涡在下游箱室脱落，气动力的方向竖直向下。此时，气动力矩方向为顺时针，与桥梁断面的运动方向相同，促进了桥断面的振动发散。在原设计桥梁断面的运动过程中，上、下表面旋涡的运动交替主导着气动力的方向，在周期内做功为正，促进桥梁断面的振动发散。

图16为0°攻角、风速为14.0 m/s 时优化方案加劲梁断面在振幅稳定阶段典型周期的压力云图。对比1/4 下稳定板和原设计方案的压力云图可以发现：增设了1/4 下稳定板后，整个流场趋于更稳定的状态，桥断面表面附近的负压区面积缩小，负压区的压强绝对值减小。在桥断面上表面，旋涡的尺度减小，负压区的压强值增大。在桥断面下表面，两下稳定板和上、下游的箱室之间形成了稳定的负压区，稳定了桥断面附近的流场。

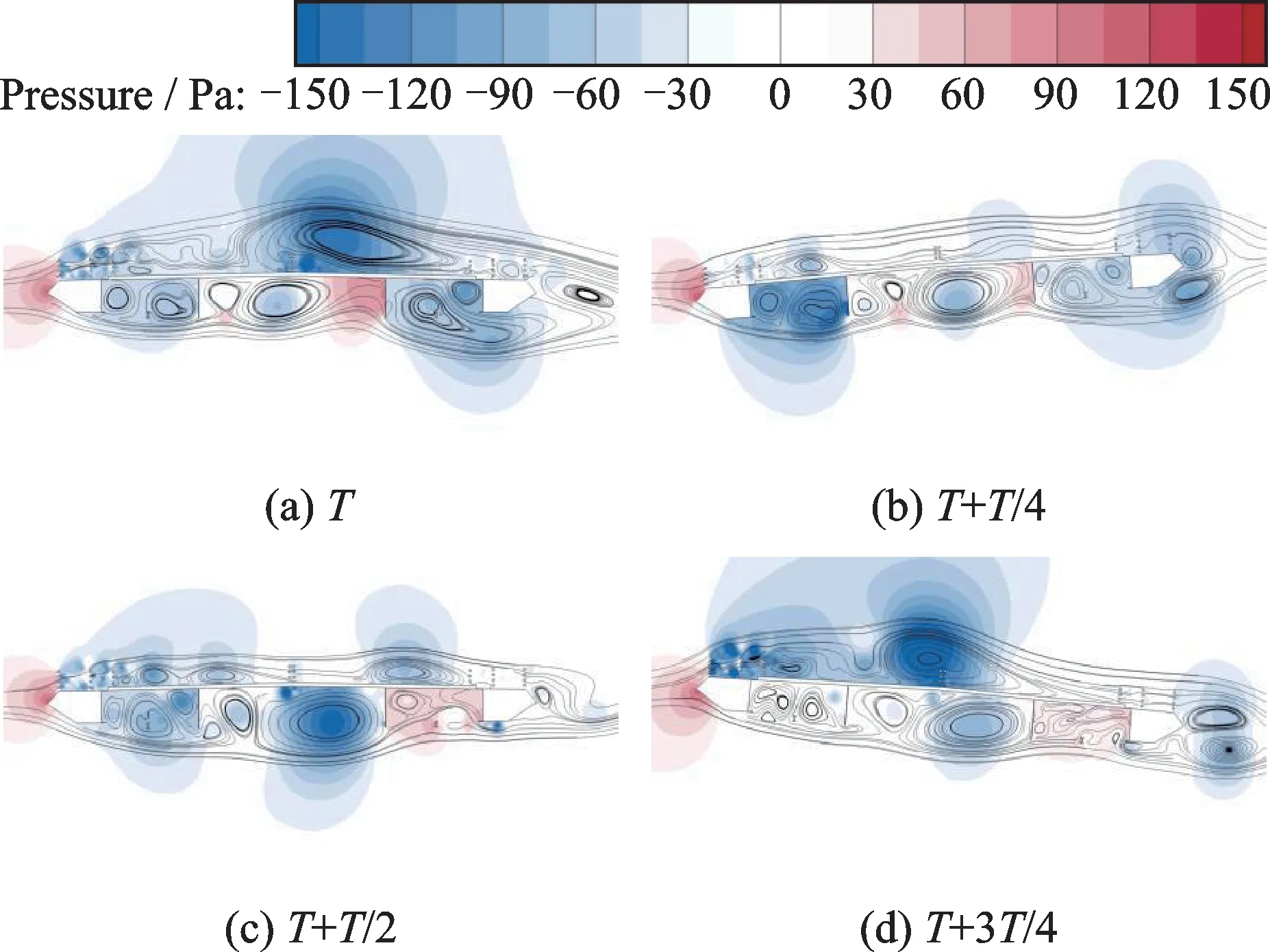
图16 优化方案瞬时压力云图（0°攻角，风速14.0 m/s）Fig.16 Contours of static pressure of optimization scheme（0°attack angle，wind velocity：14.0 m/s）

在π型加劲梁断面增设了1/4下稳定板后，削弱了桥断面上表面的旋涡的尺度，上、下表面的压力差减小，减弱了对振动发散的促进作用，有效地降低原设计π型加劲梁的振幅，改善了加劲梁的颤振稳定性能。

流场分析结果表明：相同风速下，原设计断面的旋涡的形成、运动以及脱落产生的气动扭矩与桥梁断面的运动方向相同，气动力做正功，增大了振动系统的能量。而增设1/4 下稳定板的加劲梁断面由于上表面负压区的减弱和下表面稳定负压区的存在，减弱了气动力对振动系统的输入能量值。因此，原设计断面的气动力做功输入振动系统的能量值大于优化断面的能量值，进一步验证了能量分析的结果。

5 结 论

基于数值模拟方法对某π 型加劲梁的软颤振特性及下稳定板的影响开展研究。通过数值模拟结果分析加劲梁的软颤振特性及1/4 下稳定板对加劲梁的软颤振的影响，并探讨了机理。结论如下：

（1）当来流风速大于颤振临界风速时，π 型加劲梁断面出现典型的软颤振现象，表现为振幅随风速增大而增大，振动频率随风速增大而减小。在某一风速下振动频率单一且主要以扭转模态为主。负攻角下π 型加劲梁的软颤振特性相比其他攻角的软颤振特性更为显著。

（2）在π 型劲梁软颤振的振幅扩散阶段，振动系统从外界吸收的能量大于系统消耗的能量，系统的总能量增大，加劲梁扭转位移增大。而在软颤振的振幅稳定阶段中，振动系统从外界吸收的能量近似等于阻尼消耗的能量，振动系统的总能量达到稳定，π型加劲梁的振幅趋于稳定，表现为极限环振荡现象。

（3）增设1/4 下稳定板显著降低了振动系统的总能量值，有效地提升π 型加劲梁的颤振临界风速，降低加劲梁的软颤振振幅，减小了各风攻角下扭转位移的增长速率。增设1/4 下稳定板后的π 型加劲梁的软颤振特性相比原设计的软颤振特性更为显著。

（4）来流流经π 型加劲梁断面，在上表面栏杆处和下表面的上游箱室、下检修道处分离，形成旋涡向下游发展，最后在桥断面尾部交替脱落。旋涡的产生和发展形成的升力矩与主梁的运动方向相同，气动力做正功，增大了系统的能量。在下表面增设1/4 下稳定板后，削弱了上表面旋涡的尺度，并在桥断面下表面形成了稳定的负压区，减弱了气动力对扭转振动的促进作用，降低了扭转振幅，有效地改善了π 型加劲梁断面的颤振稳定性能。