基于概率-模糊-区间混合模型和改进分枝限界法的重力坝可靠性分析方法

魏博文，张 升，袁冬阳，徐富刚

(1.南昌大学 工程建设学院，江西 南昌 330031；2.河海大学 水利水电学院，江苏 南京 210098)

1 研究背景

可靠性分析是评判重力坝服役安全性态的一种有效手段[1-2]。现有的研究成果[3-6]大多基于传统概率可靠性理论，需要明确不确定参数的概率分布。但对于实际工程而言，大多不确定参数的实测数据稀少，难以准确知悉概率分布，这在一定程度上限制了概率可靠性分析方法的应用。针对上述问题，一些学者将非概率可靠性理论应用到重力坝可靠性分析中，取得了一些有益成果[7-8]。但非概率可靠性分析方法得出的结果既不能准确度量复杂结构的可靠程度，也无相应的标准，对工程指导意义有限，通常作为概率可靠性分析结果的补充。实际上，对于难以开展原型试验的部分参数，如建基面抗剪断摩擦系数、黏聚力等，还应考虑其具有的模糊性[9-10]。因此，在重力坝可靠性分析中，若仅用一种可靠性分析方法，通常难以取得满意的结果。

结构可靠性分析考虑多源不确定性因素的影响，目前已有部分学者取得了不菲的成果。在概率可靠性分析中考虑部分变量的模糊性，已发展出不少成熟的理论[11-14]。在可靠性分析中同时考虑随机变量和区间变量的分析方法起步相对较晚，但也有部分学者已得出许多有益的结论。郭书祥等[15]和王军等[16]分别基于区间理论和凸集理论建立起结构可靠性分析概率和非概率混合模型。将概率-区间混合可靠性问题视为优化问题，DU等[17]基于传统一次二阶矩法(First Order Second Moment，FOSM)提出了一种序列迭代求解方法，并开展了灵敏度分析；姜潮等[18-19]则分别采用一次渐进积分法、响应面法和蒙特卡洛仿真(Monte Carlo Simulation，MCS)相结合的方法，提出了混合可靠性问题的高效求解模型。充分发挥Kriging模型[20]的非线性拟合能力，李刚等[21]提出了一种基于序列重要性抽样(Importance Sampling，IS)的MCS方法来计算随机-区间混合可靠度，可解决功能函数高度非线性和多设计点的混合可靠性问题；余萌晨等[22]则通过构建能正确预测功能函数符号的Kriging模型和高效全局优化主动学习策略(Efficient Global optimization，EGO)实现了随机-区间混合可靠度的高效求解。在可靠性分析中同时考虑三种不确定性，一些学者也做出了探索性研究。尼早等[23]利用凸集理论和高斯积分方法，建立了概率-模糊-非概率混合可靠性模型。杨瑞刚等[24]则将该混合可靠性模型成功应用到桥式起重机主梁结构的可靠性分析中。重力坝是极为复杂的工程，其能否正常服役事关国计民生，在可靠性分析中应当充分考虑多源不确定性因素的影响。针对这一问题，部分学者做出了一些有益的探索[25]，但仍有不确定参数的类型与分布的快速获取、考虑多源不确定性因素的影响时重力坝可靠性分析模型的科学建立及重力坝体系可靠度的高效计算等问题亟待解决。

据此，本文拟在重力坝可靠性分析中同时考虑随机变量、模糊变量和区间变量的影响，以期进一步提高重力坝可靠性分析方法的科学性和有效性。首先，明确影响重力坝服役安全性态的不确定参数的类型与分布的获取方法及重力坝可靠性分析混合模型构建与解耦方法；其次，确定重力坝单元失效准则，结合正交试验、有限元仿真和响应面法显式表达重力坝失效功能函数，建立各单元可靠性分析混合模型，再通过前述解耦方法解耦各单元混合模型并计算可靠指标；再次，对适用于框架结构的分枝限界法加以改进或更新失效准则搜索主要失效模式，同时采用窄界限法计算重力坝体系可靠度，以此评估重力坝整体服役安全；最后，以某重力坝为例，利用上述方法对选定坝段进行分析，与工程服役背景相对比，检验本文方法的科学性和有效性。

2 重力坝可靠性分析混合模型

2.1 重力坝可靠性分析混合模型服役期重力坝在水位与环境温度等因素长期耦合作用下，尤其在特大洪水、地震等突发极端荷载影响下，其筑坝材料物理力学参数和结构抗力势必与设计值存在一定偏差[26]，且难以精确获取。为合理感知与反馈重力坝的运行安全性态，可以综合利用原型、室内试验成果与大坝安全监测资料，对重力坝开展可靠性分析。考虑到影响重力坝运行性态的不确定参数众多且其类型和分布不同，若运用参数时变模型[27]、区间反演分析方法[28]等理论确定的功能函数所涉及的变量中，既有随机变量，又有模糊随机变量和区间变量，则重力坝失效的功能函数可以表示为

(1)

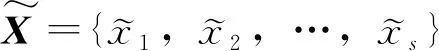
式(1)描述的是概率-模糊-区间混合可靠性分析问题，其失效概率可以定义为

(2)

式中Pr{·}为概率。

2.2 重力坝可靠性分析混合模型解耦方法针对混合模型中存在的模糊变量，可通过将其隶属函数转化为等价的概率密度函数，进而将其转化为随机变量。广义密度函数法、当量密度函数法、信息熵法等是常用的实现方法[12]。其中，信息熵法视随机变量和模糊变量的信息熵相等，信息熵[29]是用来描述变量不确定性的程度，其数学表达式为

(3)

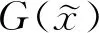
根据式(3)建立将模糊变量转化为随机变量的转换式为

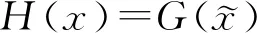
(4)

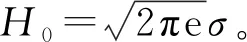
(5)

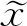
对于均值m*，可采取如下做法：1)对于隶属函数为对称型的，将对称点值作为均值；2)均值等于不考虑模糊变量模糊性时的值。

Z=g(Xall，Y)

(6)

式中：Xall=X∪X*；Y={y1，y2，…，yt}为t维区间变量，其中

(7)

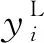
则由式(2)表达的失效概率可重新定义为

Pf=Pr{g(Xall，Y)<0}

(8)

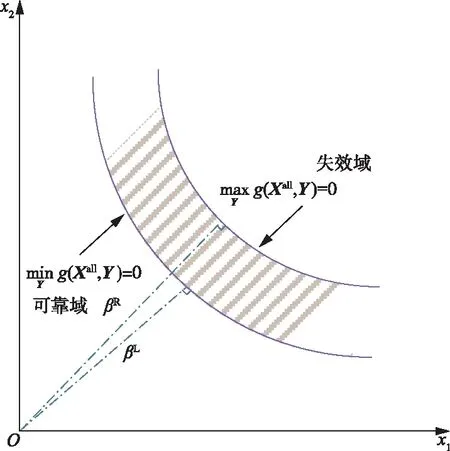
图1 极限状态区域

因而失效概率也存在上下界，可表示为

(9)

(10)

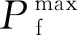
采用一次二阶矩法求解式(8)，可得优化问题

(11)

显然，式(11)中包含两层优化问题，即外层优化

(12)

与内层优化

(13)

为将式(11)中双层嵌套的优化问题转换为单层优化问题，本文利用KKT最优化条件[30]将区间变量Y转换成服从均匀分布的随机变量YU

YU～U(YL，YR)

(14)

此时，极限状态函数g(Xall，Y)可改写成g(Xall，YU)，且式(8)中可靠性指标求解的优化问题可改写为

(15)

式中：U和V分别为Xall和YU映射到标准正态空间下的随机变量；G′(U，V)为g(Xall，YU)映射到标准正态空间下的功能函数。

通过KKT最优化条件可将式(11)中的概率-区间混合模型的可靠性分析问题转换成式(15)所述的只含概率模型的可靠性分析问题，可将本文所提的概率-模糊-区间混合可靠性问题进一步转化为概率可靠性问题，进而可结合概率可靠性分析方法来评估重力坝服役安全。

3 重力坝单元可靠度计算方法

重力坝失效一般是局部损伤在环境荷载长期作用下纵深发展，形成失效路径，最终因不满足所承担的功能目标以失效模式的形式致使整体失效。为合理评估重力坝服役可靠性，本文以数值模拟结果为基础，确定重力坝单元失效准则，耦合响应面法确定重力坝单元失效的功能函数，结合重力坝可靠性分析混合模型及其解耦方法，选用成熟的可靠指标计算方法计算重力坝单元可靠度，明确重力坝可能出现的局部损伤。

3.1 失效准则根据重力坝局部可能破坏形式及筑坝材料力学性质，确定重力坝单元强度不足破坏与滑动失稳破坏的失效准则如下。

3.1.1 重力坝单元强度不足破坏 对于重力坝单元强度不足破坏而言，坝基单元失效准则多采用Drucker-Prager强度准则，坝体单元多选择Hsiegh-Ting-Chen四参数破坏准则。本文基于俞茂宏[31]提出的双剪强度理论，确定坝基、坝体单元相统一的强度不足破坏失效准则为

(16)

式中：g(i)为单元i强度不足破坏的功能函数值；ft和fc分别为重力坝材料的抗拉强度和抗压强度；σ1i、σ2i、σ3i分别为重力坝单元的第一主应力、第二主应力和第三主应力(拉为正，压为负)。

3.1.2 重力坝单元滑动失稳破坏 对于重力坝沿建基面、坝基深层滑动面、碾压施工层面及其它薄弱层面的滑动失稳，根据刚体极限状态方程与重力坝抗滑稳定分析的抗剪断公式，重力坝单元滑动失稳破坏的失效准则可表示为

g(i)=(-f·σi+c-τi)di

(17)

式中：f和c分别为滑动面的摩擦系数和黏聚力；σi和τi分别为单元i垂直于滑动面的正应力和沿滑动面的剪应力；di为单元i沿滑动面的边长。

3.2 功能函数的建立与可靠指标的计算重力坝的功能函数多为隐式非线性[1，3]，且涉及的参数众多，如何显式表征功能函数是重力坝可靠性分析中不可回避的一个问题。响应面法[32-35]应用广泛、精度较高，本文选用不含交叉项的二次多项式响应面来拟合重力坝的功能函数并结合正交试验[36]求解模型系数，响应面函数如下

(18)

式中：x=[x1，x2，…，xn]为不确定性参数；a为常数项；b=[b1，b2，…，bn]T和c=[c1，c2，…，cn]T分别为响应面函数的一次项和二次项系数矩阵；n为参数的个数。

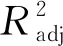
(19)

(20)

通过响应面法建立重力坝单元可靠性分析的功能函数后，运用前文提出的概率-模糊-区间混合模型解耦方法，可将其转化为仅含随机变量的常规概率可靠性问题。对概率可靠性问题而言，可靠指标计算体系成熟且计算方法众多，本文为衔接后续重力坝体系可靠度，选用JC法作为可靠指标的计算方法。

4 重力坝体系可靠度计算方法

重力坝为坝体与坝基组成的复杂三维超静定结构系统，为综合评估重力坝体系服役可靠性，需要在明确其局部损伤的基础上，寻找可能发生的失效模式，并计算其体系可靠度。重力坝的主要失效模式[38]包括以下两种：(1)坝体强度不足导致坝踵处坝体单元失效后在坝体内发展直至稳定，或坝基强度不足导致坝踵处坝基单元失效后在坝基内发展直至稳定；(2)失效发生在坝体与坝基的交界面，即沿建基面滑动失稳。为此，本文采用改进分枝限界法搜索重力坝主要失效模式，并以逐步等效线性Johnson求交法计算失效模式可靠指标，最后运用Ditlevsen窄界限法计算重力坝体系可靠度，以此综合评估重力坝系统服役安全。

4.1 改进分枝限界法失效路径是重力坝失效模式的显式载体，为合理评价重力坝的可靠性，需以坝体-坝基系统为研究对象，耦合数值模拟识别重力坝的失效路径。与系统失效概率相比，多数失效路径形成的失效模式失效概率很小，对系统失效概率的贡献不大，可予以忽略，而只需要考虑那些主要失效模式。为了在提高效率的基础上不遗漏主要失效模式，本文基于分枝限界法原理[39]，提出了适用于重力坝主要失效模式搜索的改进分枝限界法，其搜索过程如图2所示。改进分枝限界法的主要思想如下：

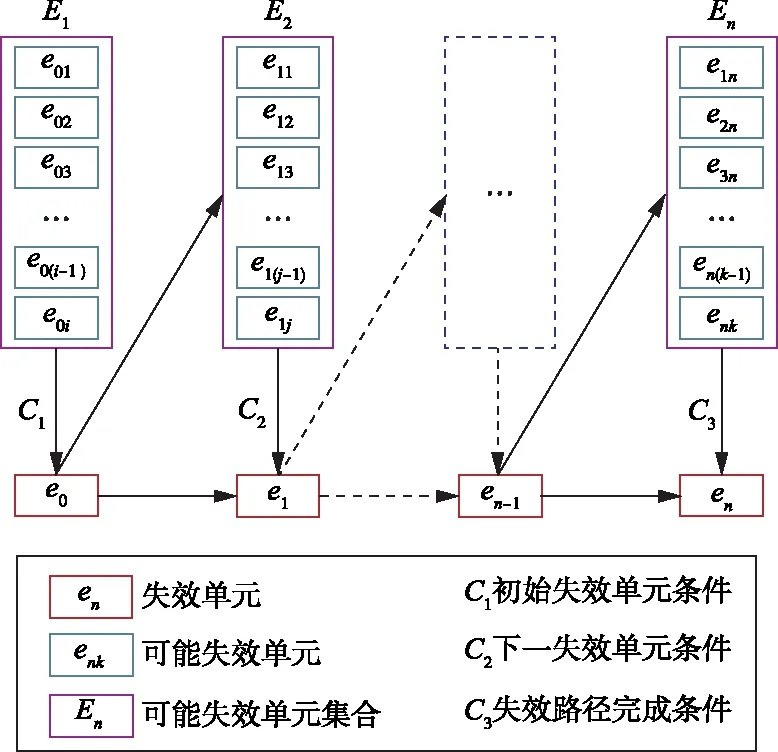
图2 改进分枝限界法搜索过程示意

(1)设置初始失效单元条件：①根据失效单元可靠指标确定主要失效模式的初始失效单元。可以定义初始失效单元的可靠指标阈值β0，如果失效路径的首个单元的可靠指标小于β0，那么此失效路径形成的失效模式通常是主要失效模式。②根据失效单元所在位置确定主要失效模式的初始失效单元。重力坝失效的发生通常开始于坝踵、坝址等已知的薄弱环节，开始于其他位置的失效路径通常能够快速收敛，所形成的失效模式对系统失效概率贡献不大，可予以忽略。

(2)设置失效路径完成条件：①设定失效路径概率稳定的可靠指标阀值βP0[40]。当组成失效路径的多个单元同时失效的可靠指标大于βP0时，认为此路径在概率上己经稳定，结束搜索。主要根据下述三个因素确定βP0。a)失效路径收敛较快，仅经历几个单元失效后，失效模式的可靠指标已满足规范要求；b)失效路径发展到βP>βP0时，后续单元的失效概率很小，由上述假设带来的误差很小；c)失效模式达到βP>βP0时，相同初始失效单元搜索得到的若干失效模式相关性很强，首次搜索出的主要失效模式在一定程度上可以代替其他失效模式。②设定失效路径完成的最大失效单元个数Nmax。在搜索过程中，一些失效路径发展深度是受限制的，此时可根据有限元尺寸确定失效路径允许的最大失效单元个数Nmax。

(3)设置搜索横向分枝数nb：在搜索失效路径的过程中，对每一个单元都进行横向分枝，才不会遗漏主要失效模式。这样操作效率较低，且横向分枝搜索出的大量失效路径形成的失效模式可能对整个体系的可靠度贡献不大，往往可以忽略。引入横向分枝数nb，可以提高失效模式搜索效率。对于重力坝而言，其静力工况下的失效路径往往是沿着薄弱环节发展的，可以近似地假设nb=1。

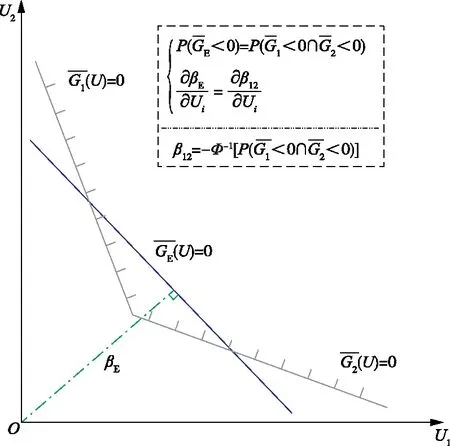
图3 两单元逐步等效线性Johnson求交法示意

4.2 体系可靠度的计算方法针对筑坝材料强度不足导致的重力坝失效，可利用前述的改进分枝限界法实施重力坝失效路径的搜索，求得坝体和坝基强度不足破坏失效模式的可靠指标。针对重力坝沿建基面的滑动失稳，考虑滑动面上所有单元的应力，重力坝滑动失稳破坏失效模式的失效准则可以表示为

(21)

式中：m为滑动面上单元总数；f和c分别为滑动面的摩擦系数和黏聚力；σi和τi分别为单元i垂直于滑动面的正应力和沿建基面的剪应力；di为单元i沿滑动面的边长。

利用逐步等效线性Johnson求交法可求得各失效模式在标准正态空间中的线性化功能函数。若两个失效模式线性化功能函数如下

(22)

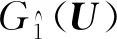
则两个失效模式间的相关系数为[42]

(23)

针对重力坝各失效模式间的相关系数较小的特点，可采用窄界限法计算重力坝体系可靠度，具体计算公式如下

(24)

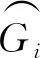
4.3 重力坝可靠性分析流程基于前述重力坝可靠性分析混合模型和改进分枝限界法，借助有限元软件计算优势[43]，总结重力坝可靠性分析流程如图4所示。

图4 分析流程

5 工程算例

5.1 工程资料和计算模型某混凝土重力坝位于吉林省境内第二松花江中游，为Ⅰ级建筑物，该坝坝顶全长1080 m，最大坝高91.7 m，坝顶高程267.70 m，上游正常蓄水位263.50 m，下游水位常年保持在193.50 m。为实时感知该坝的运行性态，坝体与坝基埋设了大量的安全监测仪器，其中，变形监测仪器主要有正、倒垂线和真空激光准直系统，坝基扬压力监测仪器主要有横向和纵向扬压水位观测孔。

以该混凝土重力坝35#典型坝段为例，该坝段坝顶长18.0 m、高79.1 m，变形监测项目主要有坝顶激光水平位移测点D35，坝基激光水平位移测点BJ35D。利用ABAQUS软件建立的该坝段数值仿真分析模型如图5所示，其坝基的模拟范围为：沿坝踵和坝趾向上、下游各延伸1.5倍坝高，沿铅直方向取120.0 m。模型共计4705个单元、4912个结点，其中，坝体共划分1321个单元、1397个结点。

图5 35#坝段有限元模型

5.2 计算参数与工况确定环境荷载变化驱动下，筑坝材料物理力学参数的演变是影响服役期混凝土重力坝运行可靠性的决定性因素，其中，坝体混凝土与坝基岩体的密度与泊松比等参数变异性小且对重力坝可靠性影响甚微，故本文将其视为确定性参数，如表1所示。

表1 确定性参数

某些参数变异性较大，且较小的变化会对重力坝服役安全产生较大的影响，在可靠性分析中必须予以考虑。其中部分参数，如混凝土、岩基弹性模量等，可结合重力坝安全监测资料(图6)，辅以有限元及区间数学，建立区间混合监控模型，反演确定[8]。此时得出的不确定性参数由于只知其上下界与变化区间，在可靠性分析中应考虑为区间变量。另有一些参数随时间变化的规律明显，如混凝土抗拉、抗压强度等，这些参数的时变模型通常可描述为Xi(t)=Xi(0)φi(t)，其中Xi(t)为某一时刻的材料参数，φi(t)为衰减函数。参考初始值Xi(0)及大坝服役年限t，借助上述时变模型获取的参数，通常视为随机变量。还有部分参数，可参考规范及原型、室内试验成果，并充分考虑其模糊性来确定，而变量类型则需要根据获取来源及信息量多寡来确定。依据上述原则，确定本文所考虑的不确定性参数的类型及分布如表2所示。

表2 不确定性参数

图6 环境量与水平变形实测过程线

作用在重力坝上的荷载并非一成不变，因此在实践中按荷载组合将重力坝受载分为几种工况。为验证本文方法的适用性，选定计算工况为正常蓄水位工况，考虑自重、静水压力和扬压力的影响，以此开展重力坝可靠性分析。

5.3 重力坝可靠性分析在确定计算工况及影响重力坝服役安全的不确定性参数后，利用前述流程对选定的35#坝段进行可靠性分析。

首先，采用信息熵法将表2中的模糊变量转化为正态分布的随机变量。对服从N(m，σ2)分布的随机变量，采样空间取为[m-2σ，m+2σ]，而对于变化区间为[a，b]的区间变量，采样空间取为[a，b]，各变量的水平数均取为5，参考表2确定各变量因素水平见表3。

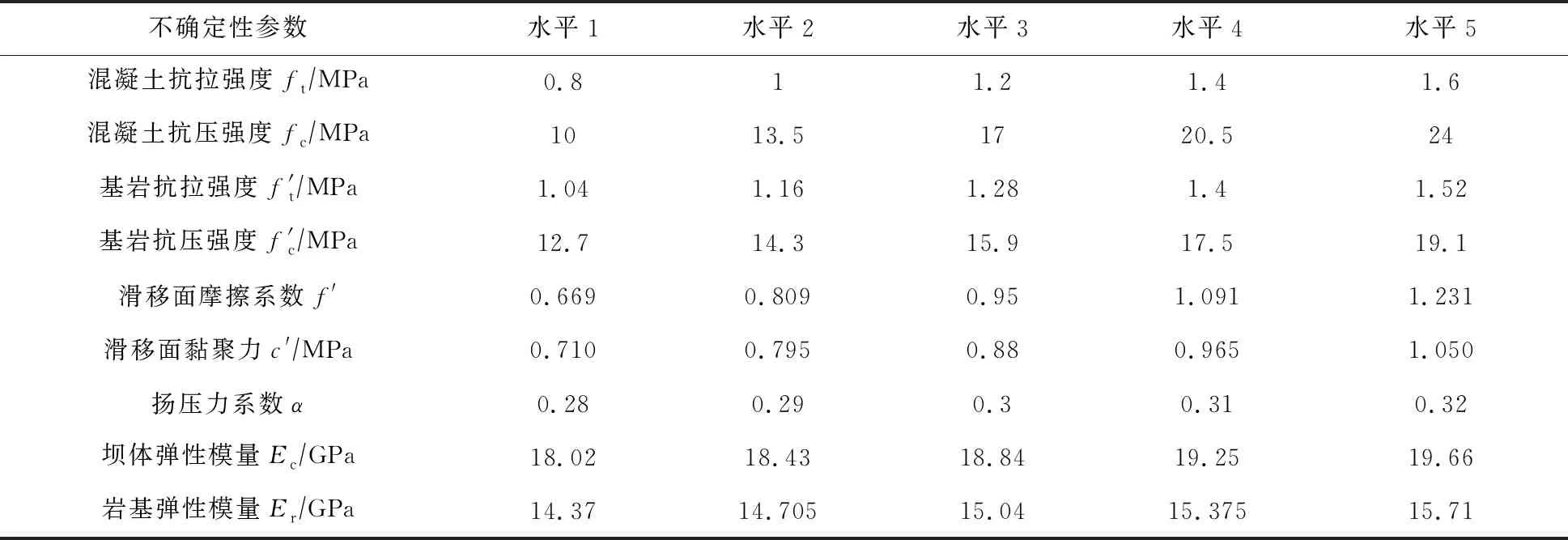
表3 不确定性参数因素水平表

其次，根据表3，对坝体、坝基强度单元和建基面抗滑单元采用正交表L25(55)开展正交试验，运用有限元软件ABAQUS仿真计算，提取单元应力，利用失效准则式(16)(17)计算响应值，运用最小二乘法拟合各单元响应面。在拟合时，为避免因参数间数值相差过大，导致响应面拟合误差加大，更改部分参数及响应值单位，使其在数量级上尽可能保持一致。

最后，对于以上述响应面表达的概率-区间混合可靠性问题，运用KKT最优化条件将其转化为概率可靠性问题，并以JC法求解其可靠指标、验算点及在标准正态空间的线性化功能函数，为后续重力坝失效模式分析及体系可靠度计算做出准备。

5.3.1 滑动失稳破坏失效模式 考虑计算坝段沿建基面滑动失稳破坏，利用式(21)更新失效准则，结合有限元计算结果拟合得到沿建基面滑动失稳破坏的响应面函数为

(25)

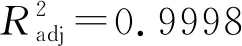
为进一步验证本文方法的有效性，将本文计算结果同文献[8]的研究成果做出相互印证：(1)文献[8]按抗剪断强度公式复核了该坝段的抗滑稳定性，计算得到的抗剪断安全系数K′c=2.59低于规范要求K′=3.00；(2)文献[8]运用非概率可靠性分析方法计算出的相应指标NR-ηH=0.926<1，表征该坝段存在滑动失稳的可能性。文献[8]结果与本文计算结果一致，佐证了本文方法的有效性。但在工程实际中，非概率可靠性分析得到的指标NR-ηH=0.926<1，只能说明结构处于非绝对安全状态，而其可靠性却无法准确度量，这对实际工程服役所能做出的指导是比较有限的。而本文建立的重力坝可靠性分析混合模型，其计算结果仍为概率可靠指标，同《标准》规定一致，工程实践指导意义明确。

5.3.2 强度不足破坏失效模式 为了分析选定的35#坝段的强度是否满足要求，采用上述理论拟合出所有单元的响应面并检验其精度后，可求出对应的可靠指标。对计算结果分析发现，仅有位于坝踵处的4个单元(坝体2个、坝基2个)和坝址处的1个单元(位于坝体)的可靠指标小于目标可靠指标βT1=4.2；其余坝体单元可靠指标均处于5～8，其余坝基单元除了坝踵、坝址附近的单元可靠指标较小外(处于6～9)，其他单元随着地基深度的增加和远离坝体，可靠指标均迅速增长至10以上。上述计算结果符合重力坝受力特点，也在一定程度上表明该坝段存在局部强度不足破坏的可能性。

为明确该坝段整体发生强度不足破坏的可能性，采用前述改进分枝限界法搜索主要失效模式。首先，需要确定主要失效模式初始失效单元的可靠指标阈值β0。考虑到重力坝在静力荷载作用下，破坏过程比较缓慢，参考《标准》，β0取为3.7。此时仅有坝踵处的3个单元(坝体1个、坝基2个)小于β0，应当作为初始失效单元，如图7所示。

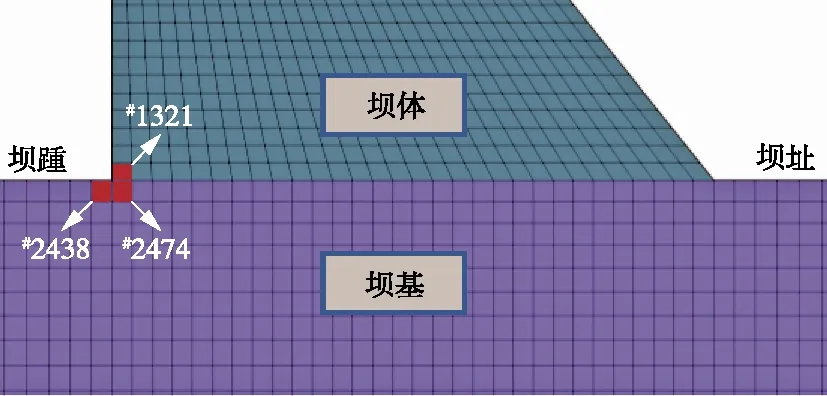
图7 初始失效单元

其次，参考《标准》和相关文献[38，40-42]，失效路径概率稳定的可靠指标阈值可取为βP0=4.2。选取初始失效单元，采用生死单元技术将其杀死，以条件可靠指标最小原则寻找下一失效单元，循环上述操作，直至失效路径概率稳定。在搜索过程中发现通常仅有1个单元条件可靠指标较小，且失效路径的可靠指标迅速增大，说明分枝数nb取为1是合理的。主要失效模式搜索结果如图8与表4、表5所示。

图8 坝体失效模式和坝基失效模式

表4 坝体失效模式

针对坝体强度不足失效模式，由表4知，形成这一失效模式的失效路径初始失效单元可靠指标较大，且各失效单元之间的相关系数均较小，导致该失效路径仅在经历3个单元失效后失效概率便趋于稳定，路径可靠指标βP1达到5.290。从计算结果及图8(a)知，坝体强度不足失效局限于坝踵，对大坝整体强度影响不大。

坝基强度不足致使重力坝失效存在2条失效模式。参考表5知，对于坝基失效模式1，初始失效单元#2438可靠指标为β20=-1.266，失效概率较大，几乎必然失效，但仅在6个单元失效后，路径可靠指标βP2便达到4.232，趋于稳定，这再次验证了重力坝单一单元的失效并不意味着重力坝整体失效的正确性。对于坝基失效模式2，初始失效单元#2474失效后，引起#2438、#2475、#2476和#2477单元连锁失效，单元失效间的相关性很强，但当失效路径达到一定深度后，应力发生重分布，随后仅在经历两个单元失效后，路径可靠指标便达到βP3=4.684，失效概率便趋于稳定。坝基两条失效模式均从地基表面向地基深处发展，对大坝防渗设施影响较小，不会对大坝抗滑稳定产生影响，仅使得大坝整体变位在一定程度上增大。采用改进分枝限界法搜索出的3条失效路径，均在经历几个单元失效后失效概率便迅速趋于稳定，对大坝的影响十分有限，这说明该坝段整体发生强度不足破坏的可能性是相当小的，基本满足《标准》要求。实际上，该大坝经过多次补强加固后，发生强度不足破坏的可能性已相当小。大坝安全监察中心第二次定期检查按材料力学法及有限元法计算了静力工况下的35#坝段的应力及整体性情况，基本能满足规范要求，与本文计算结果相互印证。

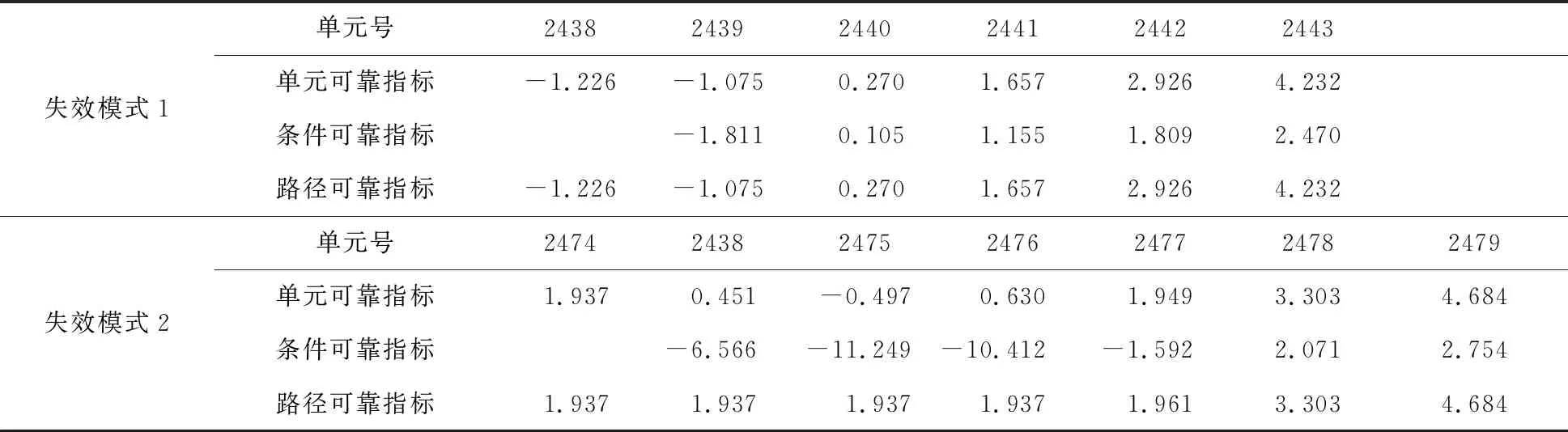
表5 坝基失效模式

在工程实践中，坝体单元的失效亦有可能引起坝基单元失效，本文为计算及说明上的方便，未充分考虑坝体和坝基的耦合作用，在实际工程分析中，应尽量予以考虑。

5.3.3 重力坝体系可靠度 求出主要失效模式的可靠指标后，为了求得重力坝体系可靠度，统计各失效模式在标准正态空间中的线性化功能函数在表6中。

表6 主要失效模式线性化功能函数

利用式(23)计算失效模式之间的相关系数，用Ditlevsen窄界限公式计算重力坝体系可靠度为5.172×10-4～5.154×10-4，对应的体系可靠指标为3.281～3.282，不满足《标准》要求。实际上，该坝的设计并非完全合理，施工质量差，混凝土强度低，稳定性及整体性差；在服役过程中，又长期经历风化、冻胀、溶蚀和坝体漏水，使得该坝一直存在一定的缺陷，虽经过多次除险加固使得该坝能正常服役，但仍有一些病险问题未能完全解决。35#坝段由于坐落在破碎带上，抗剪断摩擦系数变异性大，即使在预应力锚索加固后，仍有滑动失稳的可能性，这也是该坝一直未能解决的问题之一。大坝服役实际情况同本文计算结果吻合，再次佐证了本文提出方法的有效性。

6 结论

(1)认识到评估重力坝长期服役安全时应充分考虑多源不确定性因素的影响，通过构建重力坝可靠性分析概率-模糊-区间混合模型，可有效规避在重力坝可靠性分析中单一运用概率可靠性理论或非概率可靠性理论的局限性。(2)考虑到重力坝为三维超静定结构，失效模式众多，对适用于框架结构失效模式搜索的分枝限界法加以改进应用于重力坝主要失效模式的搜索，并利用Ditlevsen窄界限法计算重力坝体系可靠度，实现了重力坝体系可靠性的高效分析。(3)本文方法经工程实例验证，能够充分考虑工程实际，适用范围广；计算结果符合大坝运行规律和服役背景，科学性和有效性强。同时，在充分考虑工程服役实际情况的基础上，更新失效准则及失效模式的计算方法，即可利用本文建立的可靠性分析混合模型开展其他大型结构工程的可靠性分析。