考虑散体拱效应的筒仓仓壁侧压力计算方法

陈家豪，谭晗洋，陈桂香，韩 阳，何佳欢，刘超赛

1.河南工业大学 土木工程学院，河南 郑州 450001 2.河南工业大学 河南省粮油仓储建筑与安全重点实验室，河南 郑州 450001

散体储料作用于筒仓仓壁上的侧压力是筒仓结构的主要荷载，侧压力的计算是筒仓结构设计的关键问题，直接关系到筒仓的结构安全。国内外专家学者不断致力于仓储结构中散体压力的研究。原方等[1]对散体的滑动楔体进行受力分析，考虑到浅圆仓的曲线仓壁与直线挡墙的不同，根据粮堆破裂角的大小将筒仓粮堆分为3种不同工况进行水平侧压力计算。陈长冰[2]利用总体平衡法和虚位移法对筒仓粮堆压力进行了推导。李东桥等[3]摒弃Janssen理论中竖向压力分布均匀的假设，考虑粮堆有效摩擦系数分布规律得出筒仓内部压力场计算方法。这些理论虽然都给出了筒仓水平侧压力的数学表达式，但大多的筒仓仓壁侧压力[4-5]、仓底竖向压力[6-8]以及仓壁摩擦力[9-10]的试验值、数值仿真结果均与上述理论之间存在一定偏差。陈家豪等[5]认为散体竖向压力在水平面上的非均匀分布特性是主要原因之一。土拱的存在造成了土压力呈现复杂的非线性分布[11-14]，会对储料散体压力的分布产生一定影响。散体竖向压力呈现非均匀分布正是因为散体储料中存在“拱”(拱形的颗粒集合体)，在粮食散体中出现这种拱形的颗粒集合体称为“粮拱”。

对于筒仓中粮拱现象的研究，大多集中在筒仓散体物料的卸料过程中[15-17]。相比静态储粮，仓壁在卸料时受到的压力峰值可以达到静态压力的数倍[18-20]，大量的筒仓工程事故由此产生。在卸料过程中出现在卸料口附近的拱效应是仓壁压力增大的主要原因。粮食颗粒之间、粮食与仓壁之间的摩擦作用是筒仓内粮拱现象出现的直接因素，任杰等[21]从内摩擦力对储料固结条件的影响分析了成拱的主要原因。近年来，大量学者通过不同的试验方法发现了在静态储粮状态下粮拱现象的存在。罗伟洲[22]通过对砂性土的试验研究在筒仓砂堆中发现明显的应力拱效应，并阐述了可能影响这种现象的因素。

当筒仓处于正常储粮状态下，与土拱影响土压力的分布类似，粮拱也必然对储料的散体压力分布产生一定影响，各大经典理论在计算时忽略了这种现象，目前关于粮拱对仓壁侧压力影响的理论研究并不全面。蒋波等[12]根据土拱形状的理论分析计算竖向压力，并给出了考虑拱效应时的侧压力系数以及筒仓仓壁侧压力的计算方法，但其在分析过程中没有考虑到水平拱的存在。侧压力系数是计算筒仓仓壁侧压力的关键因素，多数研究选取筒仓侧压力系数时采用Rankine主动土压力系数，但Rankine理论假设仓壁为光滑材料。鉴于此，本研究将筒仓储料中存在的水平拱现象考虑在内，以筒仓仓壁面、平衡拱面和滑动面所包围的储料作为隔离体模型，取隔离体中单位微元进行受力分析，采用考虑拱效应的侧压力系数，给出了筒仓仓壁侧压力计算方法。通过与其他未考虑粮拱效应理论结果、有限元结果、实仓试验的对比分析，验证本研究计算方法的合理性与有效性，探究粮拱效应对筒仓仓壁侧压力的影响，为筒仓设计提供理论支持。

1 筒仓仓壁侧压力计算模型的建立

图1 竖直曲线形挡墙的滑裂情况Fig.1 Slip crack condition of the vertical curved retaining wall

土拱效应的机理：土体由于自重作用产生向下的变形，如果两边滑动面上可以提供足够的剪切力，这时滑动土体便会通过土颗粒相互挤压作用而将屈服应力转移至周边土体，土体的竖向应力会减小，水平向应力会增加。土拱效应的主要特点：土压力分布呈非线性；总压力大小及作用点与朗肯理论和库伦理论不同；墙底竖向平均应力小于土体自重。这是土体中竖向拱的作用机理。但土体中不仅存在竖向拱，沿挡土墙墙长方向也存在水平拱。顾慰慈[11]对挡土墙背面填土中的滑动面形状进行了系统的试验研究，其试验结果可以清晰地看出挡土墙后土体中存在水平拱现象，滑动面任一水平截面为一圆弧线，与挡墙形状相同，具有相同的曲率半径，滑裂情况如图1所示。圆弧形挡墙和直线形挡墙后水平土拱的拱曲线如图2所示。图2a中，2β角为圆弧形挡土墙背面圆弧中心角。图2b中，直线形挡墙后水平土拱的拱曲线数学表达式：

x=a2y0.357，

(1)

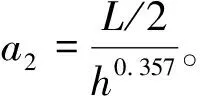
(2)

式中：φ为储料与储料间摩擦角；δ为储料与仓壁间摩擦角。

试验所得到的滑动面任一水平截面形状为圆弧线，且与挡墙的圆弧线形状相同，并具有相同的曲率半径。考虑到筒仓仓壁与圆弧形挡墙的不同，筒仓仓壁及其内部储料具有中心对称性，因此对拱曲线进行简化。简化后的平衡拱曲线与筒仓仓壁曲率相同，拱曲线的顶点与原拱曲线顶点重合，简化后拱曲线与筒仓仓壁围成的区域包含原拱曲线与筒仓仓壁围成的区域，这样可以在保证考虑粮拱现象的同时使计算更简便，计算模型如图3所示。其中，O点为筒仓中心，灰色部分为简化后拱内储料的区域。简化后的拱内储料区域中y0=R-Rcosβ+h，h为拱曲线矢高。在本文后续算例计算中，取2β为60°。

图2 圆弧形挡墙和直线形挡墙后水平土拱的拱曲线Fig.2 Arch curves of the horizontal soil arch behind the arc-shaped retaining wall and the linear retaining wall

图3 储料中水平粮拱的拱曲线及拱曲线的简化Fig.3 Arch curve of the horizontal grain arch in the storage material and the simplification of the arch curve

顾慰慈[11]的研究中，挡土墙背面填土中的滑裂体是由挡土墙墙面、平衡拱面和滑动面所包围的土体，如图1所示。朱建明等[13]研究在考虑土拱效应的挡土墙空间土压力时，为更好地体现空间土压力特点，采用的滑动面倾角(α)的取值为α=45°+φ/2(φ为储料内摩擦角)，本文沿用其α的取值。根据以上研究，本文建立的隔离体模型分为上下两个部分，上部平衡拱柱段为Ⅰ区，下部滑动面部分为Ⅱ区，Hn为平衡拱段高度，模型如图4所示。

图4 考虑粮拱效应的筒仓侧压力计算模型Fig.4 Calculation model of silo side pressure considering grain arching effect

2 考虑拱效应的筒仓仓壁侧压力计算方法

本研究计算方法基于的前提：采用简化后的平衡拱曲线，建立如图4所示的隔离体模型；α=45°+φ/2(φ为储料内摩擦角)；平衡拱柱段储料内部摩擦力竖直向下，滑动面摩擦力沿滑动面方向斜向上；将朗肯主动土压力系数替换为文献[12]考虑筒仓内部散体拱效应的侧压力系数。

2.1 受力分析

对Ⅰ区和Ⅱ区取单位微元进行受力分析，微元体如图5a和图5b所示，受力分析如图5c和图5d所示。σv为微元体顶部受到的竖向压力，Ⅰ区平衡拱柱面与仓壁平行，仓壁对储料的摩擦力(τw)方向竖直向上，平衡拱柱面上摩擦力(τf)方向竖直向下，σn和σah为微元体受到的水平压力，如图5c所示。Ⅱ区滑动面角α为45°+φ/2，仓壁对储料的摩擦力(τw)竖直向上，微元体滑动面摩擦力(τf)方向沿滑动面向上，σF为微元体滑动面上法向力，σah为微元体受到的来自仓壁的水平压力，如图5d所示。

2.1.1 Ⅰ区受力分析

竖向静力平衡方程：

图5 Ⅰ区、Ⅱ区微元受力情况Fig.5 Forces of micro-elements in zone Ⅰ and Ⅱ

σv·A上+dW+τf·l1·dz=(σv+dσv)·A上+
τw·l2·dz，

(3)

式中：dW为储料重度，dW=γA上dz，A上为Ⅰ区微元体上、下面面积；l1，l2分别为外圆及内圆弧长。

2.1.2 Ⅱ区受力分析

水平方向静力平衡方程：

σah·Aw=σF·Af·sin(α-φ)-τf·Af·cosα，

(4)

(5)

竖向静力平衡方程：

dW+σv·A=(σv+dσv)·A+τw·Aw+

τf·Af·sinα+σF·Af·cos (α-φ)，

(6)

2.2 求解隔离体内竖向压力及仓壁侧压力

2.2.1 Ⅰ区竖向压力求解

根据式(3)可得：

(7)

式中：y0=R-Rcosβ+h，将τw=tanδ·σn，τf=tanφ·σn代入式(7)可求得：

(8)

(9)

2.2.2 Ⅱ区竖向压力求解

将式(5)代入式(6)，Ⅱ区竖向静力平衡方程变形：

(10)

对式(10)两边同时对z积分可得：

σv=γ(z-Hn)+A-B+

(11)

式中：

根据边界条件σv|z=Hn=σv,1可得C2=σv,1。σv,1为Ⅰ区底部竖向压力,则：

(12)

综上，仓壁处竖向压力σv和仓壁侧压力pw,h的表达式：

(13)

pw,h=Kσv。

(14)

3 筒仓仓壁侧压力计算方法的算例验证

根据式(13)和式(14)，只要给定筒仓半径、装粮高度、储料容重、内摩擦角以及外摩擦系数等参数便可得到筒仓仓壁任一深度处的侧压力。将本研究计算结果与Janssen理论、文献[5]的计算方法、有限元结果、文献[2]实仓试验结果进行对比分析，验证本方法的合理性及有效性，给出考虑粮拱现象的筒仓仓壁侧压力计算结果，使侧压力计算结果更为精确，符合实际要求。

算例1。筒仓几何属性和储料材料属性：筒仓半径8 m，装粮高度分别为6.3 m和10 m。散料顶部平堆,储料容重8.04 kN/m3，内摩擦角25°，储料与仓壁间外摩擦系数0.40，侧压力系数根据文献[12]可得为0.435，本研究方法计算得出的侧压力结果与其他计算方法、有限元结果对比，结果如图6所示。

算例2。以郑州市东区河南省国家粮食储备库为研究对象，筒仓半径14 m，装粮高度分别为6.3 m和13.5 m。散料顶部锥堆，储料容重7.88 kN/m3，内摩擦角25°，外摩擦角21.8°，侧压力系数根据文献[12]可得为0.435，将本研究方法所得的侧压力计算结果与Janssen 理论、文献[2]实仓试验结果进行对比，结果如图7所示。

从以上两个算例可以看出，考虑拱效应的仓壁侧压力高于其他理论、有限元结果，与实仓试验结果较为符合。算例1中仓壁侧压力高于其他理论和有限元结果，主要原因是粮拱效应的影响。环分法在计算过程中采用有效摩擦系数造成本研究计算结果、Janssen理论高于其计算结果。

算例2中，本研究计算方法和Janssen理论未考虑粮堆顶部锥堆的影响，因此粮堆深度为0.3 m和1.5 m时，本研究计算结果、Janssen理论与实仓试验结果差距较大。堆高为6.3 m的算例中，粮堆深度为0.3～4.5 m 时，本研究计算结果、Janssen理论均小于实仓试验结果；在粮堆深度为4.5～5.5 m 时，本研究计算结果与实仓试验结果在某一深度处达到一致，之后本研究结果略高于实仓试验结果。

堆高为13.5 m的算例中，随着粮堆深度的增大，考虑拱效应的仓壁侧压力计算结果逐渐高于实仓试验结果。由于顶部锥堆和试验过程中不确定性因素的影响，粮堆深度为0～6.5 m 时，本研究计算结果小于实仓试验计算结果；二者在粮堆深度为6.5 m左右时达到一致，之后本研究计算结果逐渐高于实仓试验结果。原因是在式(12)包含的参数A中存在1/(H-z)项，当z值接近于H时，计算结果会存在一定误差，使得粮堆底部位置计算结果偏大。整体上看，本研究计算结果与Janssen理论、实仓试验结果具有很好的一致性，相较于Janssen理论本研究计算结果与试验实仓结果更为符合。

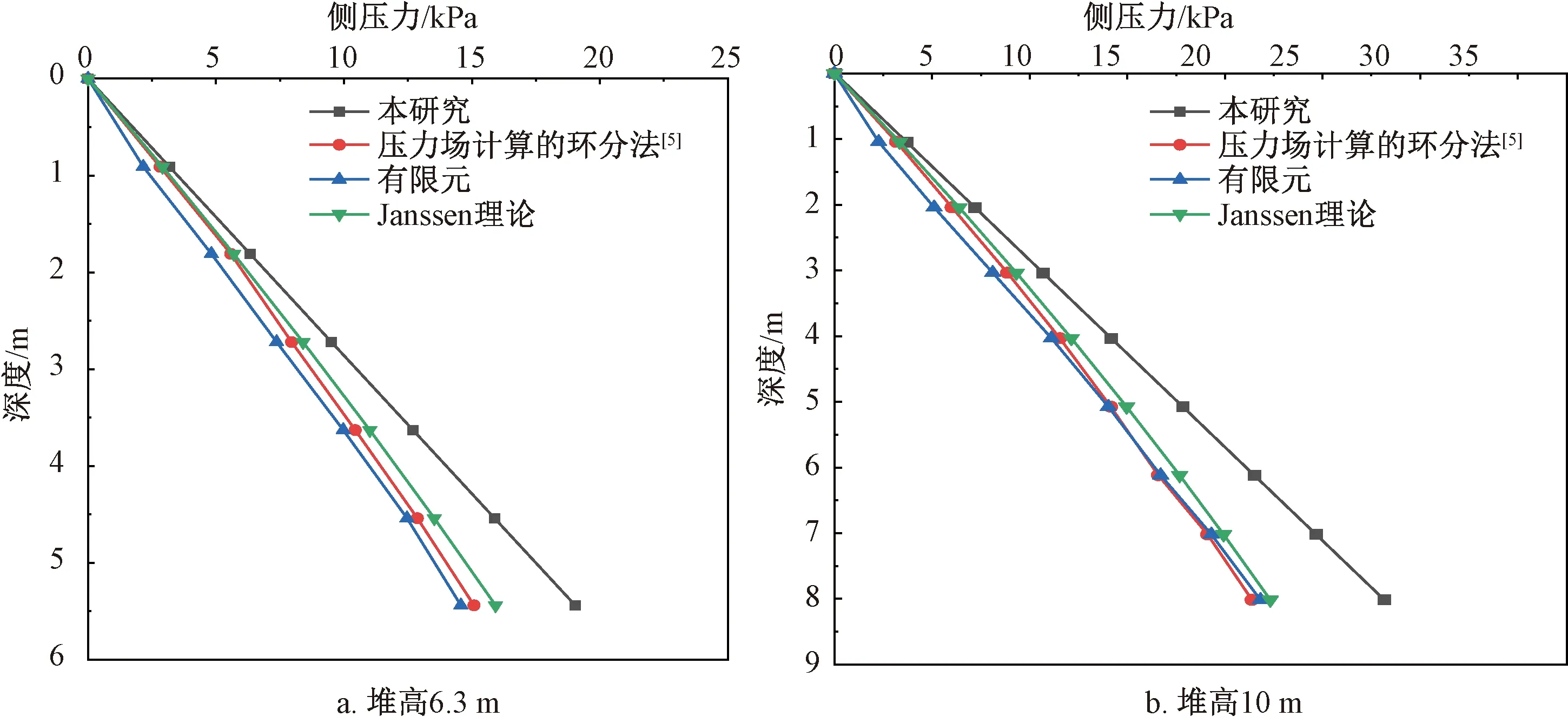
图6 堆高6.3 m和10 m时仓壁侧压力对比Fig.6 Comparison of lateral pressure at stack height of 6.3 m and 10 m

图7 堆高6.3 m和13.5 m时仓壁侧压力对比Fig.7 Comparison of lateral pressure at stack height of 6.3 m and 13.5 m

4 结论

考虑到储料中存在水平拱且圆形筒仓仓壁及储料具有中心对称性的特点，本研究从平衡拱几何形状出发，对拱曲线的几何模型进行简化，建立了考虑拱效应的仓壁侧压力计算模型，该模型是由筒仓仓壁接触面、平衡拱柱面和滑动面所围成的储料。对计算模型取单位微元进行受力分析，采用水平微分层析法求解，计算出筒仓仓壁处的竖向压力和仓壁侧压力，并与其他理论结果、有限元结果、实仓试验结果进行对比分析，得到如下结论：

相较于未考虑粮拱效应的理论和有限元结果，本研究计算结果略大，说明将粮拱效应考虑在内会使仓壁侧压力有一定程度的增大。此外，文献[5]的方法在计算过程中采用有效摩擦系数，而本研究在计算摩擦力时采用最大摩擦系数也造成了结果存在一定差异。

本研究计算结果高于Janssen理论，较低深度时小于实仓试验结果，相较于Janssen理论与实仓试验结果更为符合，一定程度上验证了本文计算方法的合理性和有效性。粮拱效应对仓壁侧压力的影响不可忽略，本文可为研究储料内部存在的粮拱对筒仓仓壁侧压力的影响提供一种思路，为筒仓设计研究提供理论支持。