基于启发式算法的货物装配策略研究

蓝机满 （惠州工程职业学院，广东 惠州 516001）

0 引 言

在一般货物的二次流通的运输环节中，货物的装配运送工作是中间最复杂、费时与费力最小的一部分，直接影响着各运输相关部门间的协作活动的质量与时间成本。随着运输信息技术的不断发展，货物运输工具的装配设计方案将完全可以通过计算机仿真模拟来自动生成，并将以此直接指导装配工作人员之间的装配运送活动，以准确提升运输货物操作环节的协调效率和质量并最终达到降低成本的目的。

本文旨在试图系统构建能自动生成车辆装配运输方案的算法，该自动算法可以实现将装载货物快准狠且有效安全地自动装入车辆车厢系统中，而且可同时满足任何给定的车辆车厢系统，自动装配完车上所有余留的货物。为了有效验证该算法中生成的自动装配工艺方案的整体可行性，本文利用了SharpGL图形包来对生成工艺的整体方案的正确性做了进一步验证，实验最终结果表明，该算法可以较为合理、高效、经济地设计完成自动化装配。

国内学者提出了以下观点：张游天等（2021）提出，在美国时下比较广泛流行使用的对货物进行自动化装配问题的分类研究方法[1]；江峰等（2020）提出，大规模货物列车，在运行阶段需要通过编制启发式的算法，对物流运输方式进行优化整合[2]；王张峰等（2017）提出，基于启发式算法的托盘货物优化装载方法，依据货物数量进行自动装配继而将所有可能同时出现的车辆车厢的货物进行自动化装配[3]；郑炜等（2016）提出，在货物混装模式中，可以通过启发式的算法，对货物装载问题进行研究，提高货物运输质量[4]；宿伟伟等（2007）提出，多品种货物混装配载模型可以通过启发式的算法，对货物的运输方法进行计算与整合[5]；徐海东等（2004）提出，启发式算法在非满载货物运输优化调度中的应用，需要通过对启发式算法进行预判，进而优化物流运输中的路径，对风险起到一定的规避作用[6]。

1 货物自动化装配问题

1.1 货物自动化装配概述

货物集装箱的计算机自动化的装配及设计问题，就是指怎样利用现代工业计算机通过自动编程把各种型号、不同规格的一些大型特殊包装货物自动、合理、准确地安装到专用车厢系统内的装配系统方案。货物方面的综合装配设计技术问题实际上已经不是某一类最原始、简单的技术设计理论问题，而是由许多不同形式和种类各异的技术装配和工艺问题所共同组成的关于装配设计的综合理论问题。根据不同层次的研究内容和约束限制条件，可以适当地将其研究细分为两个不同阶段的分支。货物装配最优化是一类多目标组合的优化完全问题，其理论本质仍然是NP-HARD问题，而目前解决NP问题的较为传统的方法就是利用元启发算法模式不断地去找寻算法，不断地在不同的空间中找寻最优解。

1.2 货物自动化装配问题的分类

一个三维空间的装配问题是货物的自动化装配。近些年来有较多的分类方法。将装配问题大致划分为两类：装配多的车辆车厢问题；集装箱车辆车厢问题。

1.3 货物自动化装配问题的技术难点

实际上，在运输过程中，货物的形状、数量复杂，并且在整个货物车厢的尺寸不确定的情况下，解决好对整体货物的准确自动装配，并且同时又要能满足在货物自动准确装配作业时存在着的许多约束性条件和可控制性技术条件是当前面临着的重要技术难点。

在实际进行货物的组装与摆放或运输活动时，货物可能就存在着以下7种不同类型的实际装配、摆放及运输活动状态，在货物的包装结构的实际几何形状是长方体的情况下，仍然有6种不同类型的实际装配状态。见图1。

图1 长方体6种货物摆放图

2 核心算法

2.1 算法的基本思想

本文的目的主要是在求解货物的自动装配法约束原则下，寻求到一种以划分平面理论为基础的求解货物在自动化装配下的误差的方法。将车厢的底部分为20个等面积的小格。如果想要提高自动化装配系统的标准度，可将车厢划分为若干个更多数量的小格子。

假设货物的装配层数要求为NumLayer，货物将只有图1所示的第一种和第二种放置状态。将当前被选择到的货物号码的长记为Li，宽记为Wi，高记为Hi；由原点出发，然后沿着X轴正方向不断叠加查找，找到第一个空白小格子，再开始依次累加长，记小格子的累加长为Lsum，当Lsum≥Wi，从找到的第一个空白小格子的位置开始顺着Y轴正方向依次不断累加小格子的宽，直至到达车厢内的底面边缘或小格子上已经填上顺序编号，则停止累加。记小格子的累加宽为Wsum，当Wsum≥Li，就可以判断出车厢长度与货物长度之间的关系，在累加过程中，若不能同时满足Lsum≥Wi、Wsum≥Li的条件时， 就需要变换到图一货物的放置状态，经过不断操作得出货物高度小于车厢内高。

假设车厢内长为Lcarriage，宽为Wcarriage，高为Hcarriage。通过公式（1）与公式（2）将货物放置状态设置为图 1 所示的第一种和第二种放置状态时，单个货物进行装配时的一般约束条件为公式（1）（2）。

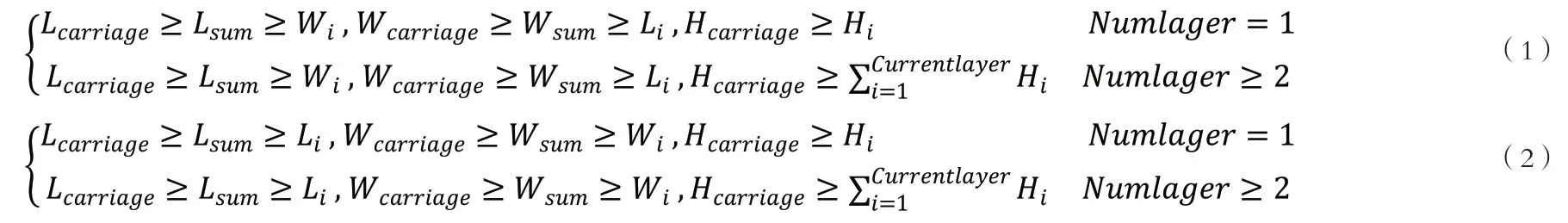
2.2 改进思想

上述计算模型提供了最终货物装配的另一个基本思路，但是算法仍然存在着以下三个显著缺陷：算法在对最后的货物和最终装配的设计进行处理时，只先考虑了如图1所展示的状态；算法有贪婪性，让算法无法实现最优解；在一定的车辆数量下，会要求其装配货物的数量、体积等，但是此算法下对此要求无法达到百分之百符合，而且还存在问题。启发式的算法需要将货物运输的体积与运行方式计算进去，套用启发式算法公式，对之后的模型建设进行相关处理，以提高物流运输的效率。

3 实验仿真与分析

3.1 实验配置

本文作者拟尝试选用一种基于微软C语言平台环境下所开发出的OpenGL函数库仿真软件SharpGL来仿真模拟以及对装配的算法结果进行仿真模拟和验证。SharpGL开发者们应该可以比较轻松地使用微软视窗的Windows操作系统中的Forms或WPF，应用中能够轻松实现使用OpenGL函数库来开发出图形可视化设计。借助SharpGL，可以保证在较短期范围内迅速实现和建立出对装配算法效果的模拟分析及仿真。

3.2 实验结果

本实验对算法进行了操作与验证，该实验具有三个约束条件如下：先寻找一批货物和卡车，要求都为长方形，需要将给定货物装配到给定的车辆车厢中；货物可以分为4类，其中第一、二、三类不可以混装，第四类可以混装；要求货物底面接地，按照表1的车厢尺寸放置货物，当 NumLayer 为 1 时，1 层就是货物装配 ，并且采用表2的货物尺寸。表1和表2分别是给定的车辆车厢尺寸和给定的货物尺寸。

表1 给定的车辆车厢尺寸mm

表2 给定的货物尺寸mm

4 结 论

三维货物中的装配约束问题是另一个难以完全被有效的方法解决的NP-HARD问题，当对三维货物中装配的各种约束条件和限制条件都给定很多遍时，很难得到一个完全满意的结果。

本文拟利用研究结果提出来另一种基于平面分割的设计算法方案，提供给广大用户一种基于集装箱货物的自动化装配的算法方案，但研究发现目前本方法设计及算法模型设计仍存在很多局限，如尚不能很充分合理地利用车厢内的面积和空间，对于各种异构货物集装箱的自动装配，尚还不能很充分地满足车厢空间布置需求以及实现集装箱货物自动化装配系统的基本约束条件和设计条件。基于存在的各种问题，本文已分别提出了对其改进的举措和一些新想法，预计今后将会在进一步的研究调查工作中给出一些相关的数据以支持和证明。