改进PSO-LSTM的水文时间序列预测

张洋铭，万定生

(河海大学 计算机与信息学院，江苏 南京 211100)

0 引 言

在近年来数据驱动的预测方式准确度不断提升，水文时间序列预测取得了较大进展。除了经典的物理模型、BP、SVM等神经网络外，易云飞等[1]提出了结合时间序列分析和卡尔曼滤波的优化方法，有效地预测水位短期内趋势。余洋等[2]采用WNN-SVM组合模型对流量进行预测，验证了改进的SVM模型对水文时间序列预测的精度有所提高。

这些算法在数据量丰富、规律明显的大江大河的预测上取得了成功，但中小河流数量众多，研究期短，数据量少，规律特殊。长短期记忆神经网络(LSTM)凭借其优势，在该领域表现突出。

Widiasari等[3]将LSTM模型应用到小流域洪水预报中。Zhang等[4]研究了水位预报中LSTM的适用性，验证了其准确度。Kratzert等[5]证实了LSTM在小流域水文时间序列预测上有较强的预报能力。Hu等[6]验证了在降雨及径流方面，LSTM的预报精度较高。冯钧等[7]提出基于LSTM-BP的组合模型预测方法，提高了中小流域预报的准确度。

上述文献在实验中，LSTM参数选择往往采用试错法[7]与一些简单的优化，而忽略了模型参数的影响。中小河流水文时间序列具有复杂性高与不确定性的特点，且水文模拟优化过程往往是强非线性的[8]。本文改进粒子群优化算法(PSO)，结合注意力机制与LSTM建立组合模型，使其在中小河流水文时间预测上产生更好的效果。

1 相关研究

1.1 LSTM原理

长短时记忆神经网络(long short-term memory，LSTM)作为一种特殊的循环神经网络(recurrent neural network，RNN)，其神经元能够将当前时刻信息，传递到下一时刻[9]。循环神经网络的具体结构请参见文献[9]。

然而，梯度爆炸与消失是RNN在处理时间序列最容易出现的问题，因此导致对于时间周期稍长的序列特征难以学习[10]。为了解决这个问题，LSTM被提出。

图1是LSTM神经元的内部结构示意图。当前时刻为t，ht-1、ct-1分别为(t-1)时刻序列神经元的隐藏状态变量与细胞状态变量，xt为当前时刻的输入序列。信息被输入到神经元，依次通过内部遗忘门ft、输入门it与输出门ot，计算得到当前时刻t序列的ht与ct。ht与ct继续传入下一时刻神经元的同时，会传入输出层，生成时间序列在t时刻的预测结果yt，组成结果集

ft=σ(Wf*[ht-1,xt]+bf)

(1)

遗忘门决定了从当前时刻状态中遗忘什么内容。根据上一时刻神经元状态，遗忘门会读取ht-1和xt，输出一个在0(“完全抛弃”)到1(“完全保留”)之间的数值给每个在细胞状态ct-1中的数字，决定遗忘程度。σ为Sigmoid激活函数

it=σ(Wi*[ht-1,xt]+bi)

(2)

(3)

输入门决定让多少新的信息加入到当前时刻中。it根据式(2)决定哪些信息需要更新，式(3)通过激活函数tanh备选用来更新的内容，共同对细胞状态进行更新

ot=σ(Wo*[ht-1,xt]+bo)

(4)

ht=ot*tanh(ct)

(5)

输出门首先通过式(4)决定细胞状态哪个部分将被输出，再通过式(5)，tanh激活函数处理，输出到下一层细胞。

图1 LSTM内部结构

神经元的细胞状态变量ct在与其它单元传递信息中，保持线性交互，能够保持长时序列特征不变，因此使得模型在训练过程中避免出现梯度爆炸与消失的问题，保证了LSTM具有长时记忆能力。使得神经网络大大提升了对时间序列的记忆能力，更适用于处理时间序列。

1.2 粒子群优化算法

粒子群优化算法(particle swarm optimization，PSO)定义请参见文献[11]。作为一种进化计算技术，通过种群中的个体间协作和相互之间信息传递，让群体求解空间不断更新，在问题的演化中产生从无序到有序的过程，从而得到最优解。原理描述如下：

首先在需要求解的一个d维搜索空间中,初始化m个粒子。求解过程中算法迭代n次。假设在第t次迭代中，第i个粒子 (i=1,2,…,m) 的位置向量为xi=(xi,1,xi,2,…,xi,t)， 速度向量为vi=(vi,1,vi,2,…,vi,t), 第i个粒子至今为止搜索到的最优位置为pbesti，整个种群至今为止搜索到的最优位置为gbesti。

那么，在寻找最优解的过程中，每个粒子在第t次迭代后下一时刻的速度和位置，分别按照式(6)、式(7)进行更新

vi,t+1=w*vi,t+c1*rand*(pbesti-xi,t)+c2*rand*(gbesti-xi,t)

(6)

xi,t+1=xi,t+λ*vi,t+1

(7)

其中，w为惯性权重，影响粒子收敛速度；c1和c2为学习因子，用来调整个体与群体最优解的比例；rand为[0,1]之间的随机数；λ为速度系数。

由公式原理可知，粒子速度更新的过程，有3个影响因子：粒子自身之前时刻对目前状态变化的影响、粒子自身迭代过程中的变化、群体搜索结果对个体粒子的影响。

2 构建改进PSO-LSTM组合模型

针对PSO与LSTM的原理，结合中小河流水文数据的特点，本文对算法进行以下改进，构建改进的PSO-LSTM组合模型。

2.1 改进PSO算法

粒子群算法在寻找最优解的过程中容易陷入早熟和收敛速度慢的缺陷。针对此问题，本文引入变异算子，将粒子群体趋于一致性与粒子变异结合，增加粒子多样性和寻优能力。同时对惯性权重进行调整，将固定权重改为非线性变化权重，改善了收敛精度和速度。在此基础上，加入对收敛标准的优化，使算法在全局寻优过程中保证效率。

2.1.1 改进惯性权重

由PSO算法计算公式可知，粒子变化速度公式中w为惯性权重，是维持着上一时刻速度趋势的系数。w系数大，全局寻优能力强，w系数小，局部寻优能力较强。因此，固定的w减弱了算法的全局寻优能力，并减慢算法的收敛速度。本文提出利用非线性变化惯性权重来提高PSO的性能。将w改为如下形式

(8)

其中，wmax和wmin分别为w的最大值和最小值；t为当前代次数；tmax为最大迭代次数。w随迭代次数变化图像如图2所示。

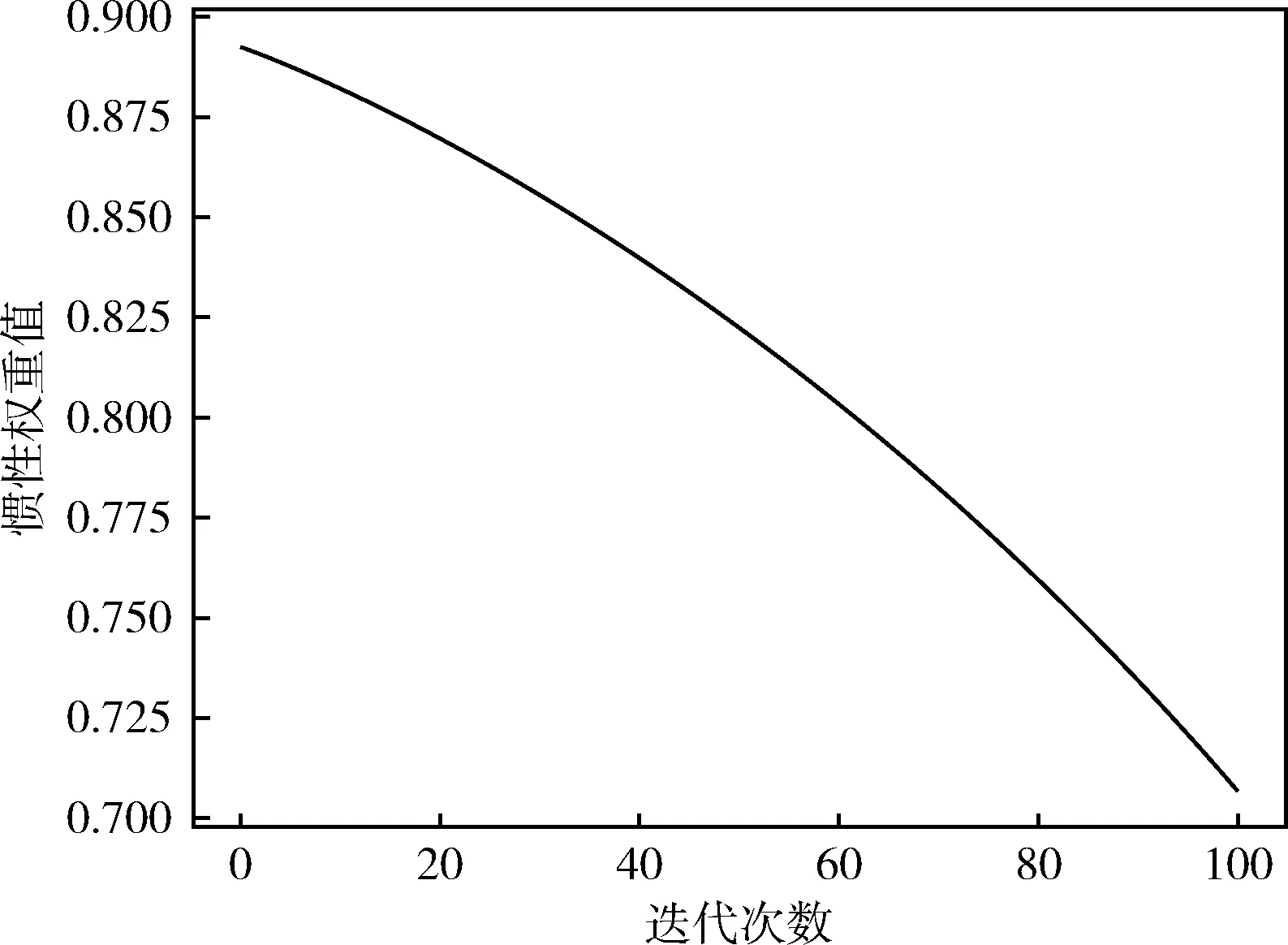
图2 惯性权重变化曲线

图2为改进后的惯性权重变化曲线，当t较小时，w接近于wmax，并且w的减少速度也较慢，保证了算法的全局寻优能力；随着t增大，w以非线性递减，并且w的减少速度逐渐增加，保证了算法的局部寻优能力。通过改进惯性权重，从而使原来较弱寻优能力的算法能够在前期快速搜索全局最优解，后期增加局部解的寻找，寻优能力更强。

2.1.2 改进粒子种群

除了对惯性权重的改进，为了使粒子更加丰富，本文提出对粒子种群进行改进。

在遗传算法中有一个重要的概念：变异算子，基本思想是模拟基因突变，产生更加多样的种群，在求解全局最优问题上保证了良好的鲁棒性。本文参考了该算法中变异算子的思想，在粒子群算法中增加改进粒子种群的自适应变异操作，主要目的在于维持种群的多样性，减小粒子在搜索过程中同化的概率。可以有效地防止算法过早收敛于局部最优解，从而增强算法的全局寻优能力。自适应变异的概率公式为

(9)

其中，t为当前迭代次数，tmax为最大迭代次数。该方法在实验过程的实现如算法1所示。

算法1：

(1) For i in range(粒子数)

(2) 根据自适应变异公式判断是否rand>σ

/*rand为[0,1]之间生成随机数*/

(3) For j in range(搜索纬度)

(4) Do 更新最优解

(5) End for

(6) Do 记录gbest， pbest

/*pbest:个体最优， gbest:全局最优*/

(7) End for

(8) For t in range(最大迭代次数)

(9) Do 更新gbest， pbest

(10) End for

在该算法中，往单个粒子搜索最优解时加入自适应变异公式，随机rand数在纬度搜索前对全局最优解更新做出限制。随着迭代次数增加，自适应变异公式呈非线性增加，随机rand数大于自适应变异公式σ的概率减小，从而随着粒子数增加，粒子群变异的几率减小。从而可以保证粒子群的多样性，减少粒子受其它粒子影响，逐渐同化，陷入局部最优的风险。

2.1.3 极值扰动

由粒子群算法的原理可知，单个粒子更新的状态会受到当前群体最优值和个体最优值的双重吸引。这促使粒子向由个体当前位置、个体历史最优位置与群体当前最优位置所构成的扇形区域内移动。使得搜索范围得不到扩散，粒子陷入“早熟”。

在粒子的收敛判断中，种群适应度方差δ2反映了种群个体的聚集程度，δ2越小，则种群个体的聚集程度越小。因此，在标准的粒子群算法中，δ2会随着迭代次数越来越小，粒子群可能会过快由分散变密集。

本文对群体最优值进行扰动操作，扰动公式为

Gbest=gbest+ε

(10)

其中，gbest是群体的全局极值在第d维的分量，ε为随机扰动量，是第t次迭代，粒子在第d维位置的平均值，乘随机数rand得到的。Gbest为扰动后的全局极值。对极值进行扰动之后效果如图3所示。

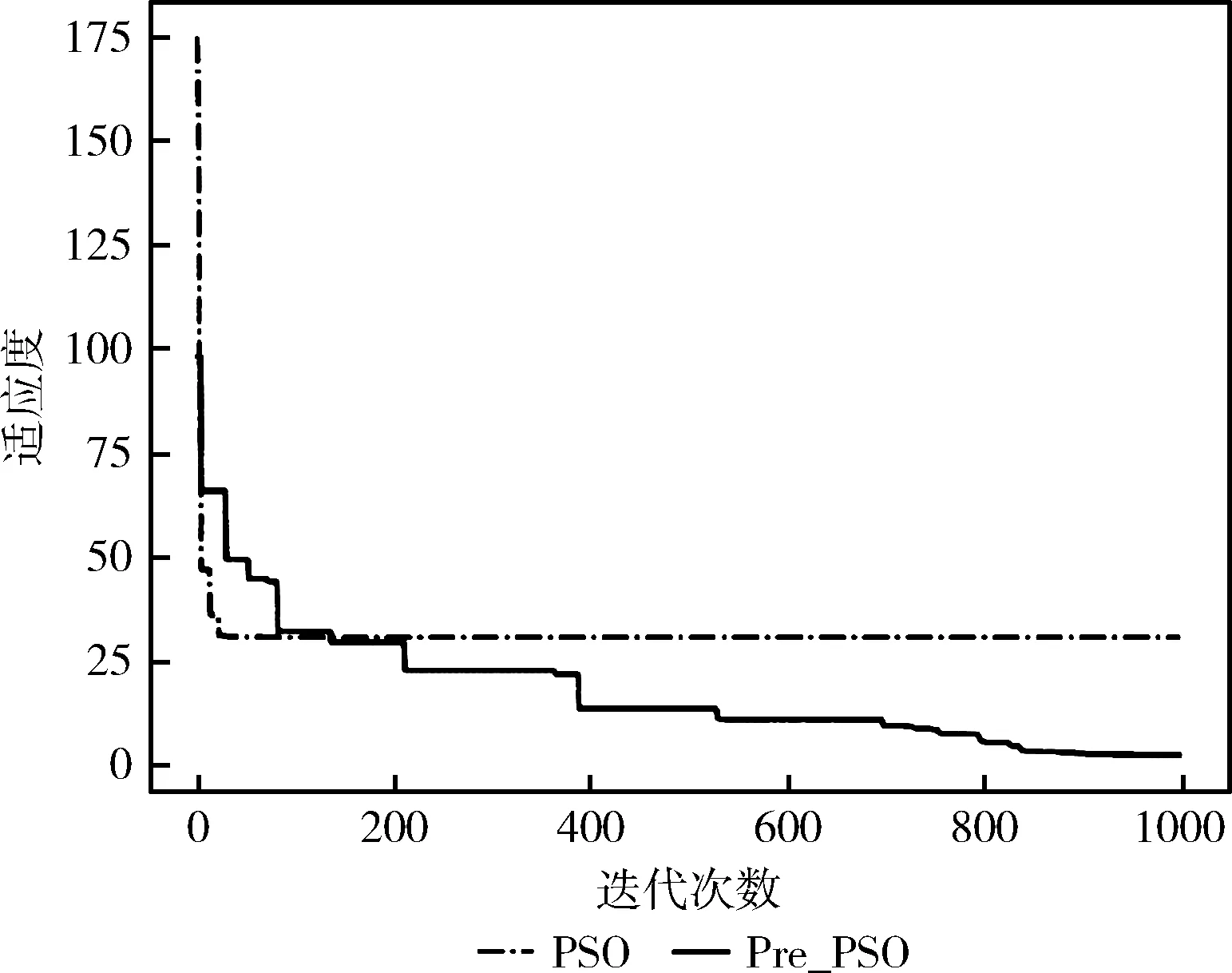
图3 Rastrigin适应度曲线

图3为采用Rastrigin函数的结果验证对比图，PSO为未改进的效果，Pre_PSO为改进之后的效果。根据结果来看，粒子在更新自己状态过程中，加入了随机扰动变量，根据扰动后的全局状态Gbest进行更新，使得单个粒子在运动过程中受群体最优位置影响情况减小，粒子会向未搜索到的方向倾斜，有效地扩大了粒子本身搜索范围。在群体中防止过早早熟收敛现象。从图像表现可以看出减缓收敛的趋势以及跳出局部最优的能力。

2.2 改进LSTM模型

LSTM在长时间序列处理上表现良好，但序列中不同特征重要程度具有差异，影响信息选择。针对此问题，本文引入注意力机制(attention mechanism)对LSTM模型进行改进。

采用注意力机制目的是实现LSTM中资源应用高效，一般步骤如下：信息输入；计算注意力分布α；由α计算出输入信息xi的加权平均作为输出结果输入到分类器。本文基于缩放点积模型(scaled dot-product attention)，在实验过程中与LSTM模型结合计算如下

αi=softmax(s(xi,q))

(11)

(12)

式中：αi为注意力分布，xi为输入信息，q为序列向量，d为缩放系数，引入注意力机制与LSTM的记忆单元结合，模型如图4所示。

图4 基于注意力机制的LSTM模型

图4为基于注意力机制的LSTM模型原理图，将一个预测序列元素q，计算键(Key)的概率分布并传递到值(Value)上(Key与Value是Source构成元素)，得到每个Key对应Value的权重系数，加权求和后，从而输入到LSTM网络实现时间序列预测，不断循环训练。这个过程体现了注意力机制对差异特征进行选择的特性：从大量信息中选择出关键部分，不用将所有特征都输入到神经网络模型中计算。根据训练好的权重对序列进行预测，使多变量输入的LSTM模型对时间序列的处理能力更强，预测准确率更高。

引入注意力机制可以提高对时间序列特征的细粒度提取能力，实现高效信息优化与神经网络训练能力。

2.3 基于注意力机制的改进PSO-LSTM模型

将改进后的粒子群算法与基于注意力机制的LSTM结合建立组合模型，将其称之为Pre_PSO-LSTM模型，实现过程描述如下：

步骤1 对原始数据进行去噪、均值归一化、划分数据集等预处理；

步骤2 初始化参数。确定粒子种群规模、迭代次数、学习因子以及位置和速度取值的限定区间；

步骤3 初始化粒子的位置和速度。随机生成一个种群粒子xi,0(α,ε,h1,h2),i为粒子个数，优化的超参数为α，为LSTM的学习率，ε为LSTM的epochs，h1,h2为双层隐含层神经元数。

步骤4 初始化LSTM。根据式(11)，引入注意力机制，对Dense进行处理，转换维度后与神经网络相结合。

步骤5 确定粒子的评价函数。将步骤2中得到的粒子xi,0对LSTM的参数赋值。将个体xi的适应度定义为

(13)

将训练集与测试集的评价指标融合作为适应度函数。防止只利用训练样本的拟合误差作为适应度值，得到的模型预测效果是过拟合的。

步骤6 标记每个粒子当前位置xi并计算对应的适应度值，确定极值并标记历史最佳位置。

步骤7 在循环迭代中，采用算法1更新粒子速度和位置并计算新的适应度值，根据式(10)对极值进行扰动更新粒子个体极值和群体极值。

步骤8 满足算法最大迭代次数后，将测试集输入利用最优粒子训练好的改进后的LSTM模型，输出预测结果。

改进的PSO-LSTM模型针对于水文时间序列预测具有以下优势：

水文时间序列具有非线性、非平稳性和多时间尺度变化的特征，针对水文时间序列数据复杂且高维的问题，组合模型通过改进LSTM模型将其与注意力机制相结合，能够更好地挖掘出各组信息对序列预测的影响，筛选出有效的特征，提高水文数据预测的精度。由于水文领域的特殊性，中小河流观测数据的完整性无法保证，连续的数据记录往往存在异常点，这些噪音对模型训练产生影响，上述提出的变异算子算法与极值扰动方法能较好地减少异常点对粒子群算法的干扰。同时，水文数据变化幅度大，时变速率快，预见期短，改进惯性权重的方法不仅提高了PSO算法的寻优能力，也更适用于组合模型预测具备此特征的中小河流水文时间序列。

3 实验与分析

3.1 实验准备

实验基于TensorFlow2.0.0框架进行编码，所用平台为PyCharm2018.2.2x64，搭载的操作系统为Windows 10。

采用的数据集为屯溪流域从2016年1月1日至2016年8月31日共计5800个小时雨量及水位数据。屯溪水文站位于屯溪流域的汇流出口处，根据屯溪流域的雨量站点情况，依据相关性分析法，将该流域划分为11个单元流域，对应11个关键雨量站，分别为黟县、儒村、岩前、呈村、上溪口、五城、屯溪、大连、左龙、休宁和石门。出口断面水位主要与该11个雨量站的雨量有关，因此采用雨量站雨量作为模型自变量之一。图5为屯溪流域相关雨量站分布图。

图5 屯溪流域相关测站分布

数据集被分为两部分，一部分是训练数据共4060条，用于训练调整模型权值和系数;另一部分是测试数据共1740条，为汛期数据，用于测试预测效果。预热期为6小时，预见期为3小时，运用前6小时11个站点的面雨量以及当前小时屯溪的水位来预测未来水位。

3.2 评价指标

根据《水文情报预报规范》，对水文时间序列预测的评价指标可以采用绝对误差、相对误差、均方根误差、决定系数等，本文采用均方根误差与决定系数。

3.2.1 均方根误差

均方根误差(RMSE)，在整个预报的过程中，预测值与真实值之间的偏差的程度，值越小表明结果与真实值相差越小，其计算公式如下。其中，ytest为测试样本真实值，ypre为预测值，n为测试样本数

(14)

3.2.2 决定系数

决定系数(R2)，反映因变量的全部变异能通过回归关系被自变量解释的比例。值越接近1，表示模型拟合效果越好。计算公式如式(15)所示。其中，ytest为测试样本真实值，ypre为预测值，ymean为平均值

(15)

3.3 实验结果与分析

为了验证改进粒子群算法的效果，采用原始PSO算法以及改进后的Pre_PSO算法分别对5维sphere测试函数寻优，进行对比实验，两种算法各迭代1000次。将其结果进行处理放大呈现，得到适应度曲线如图6所示。

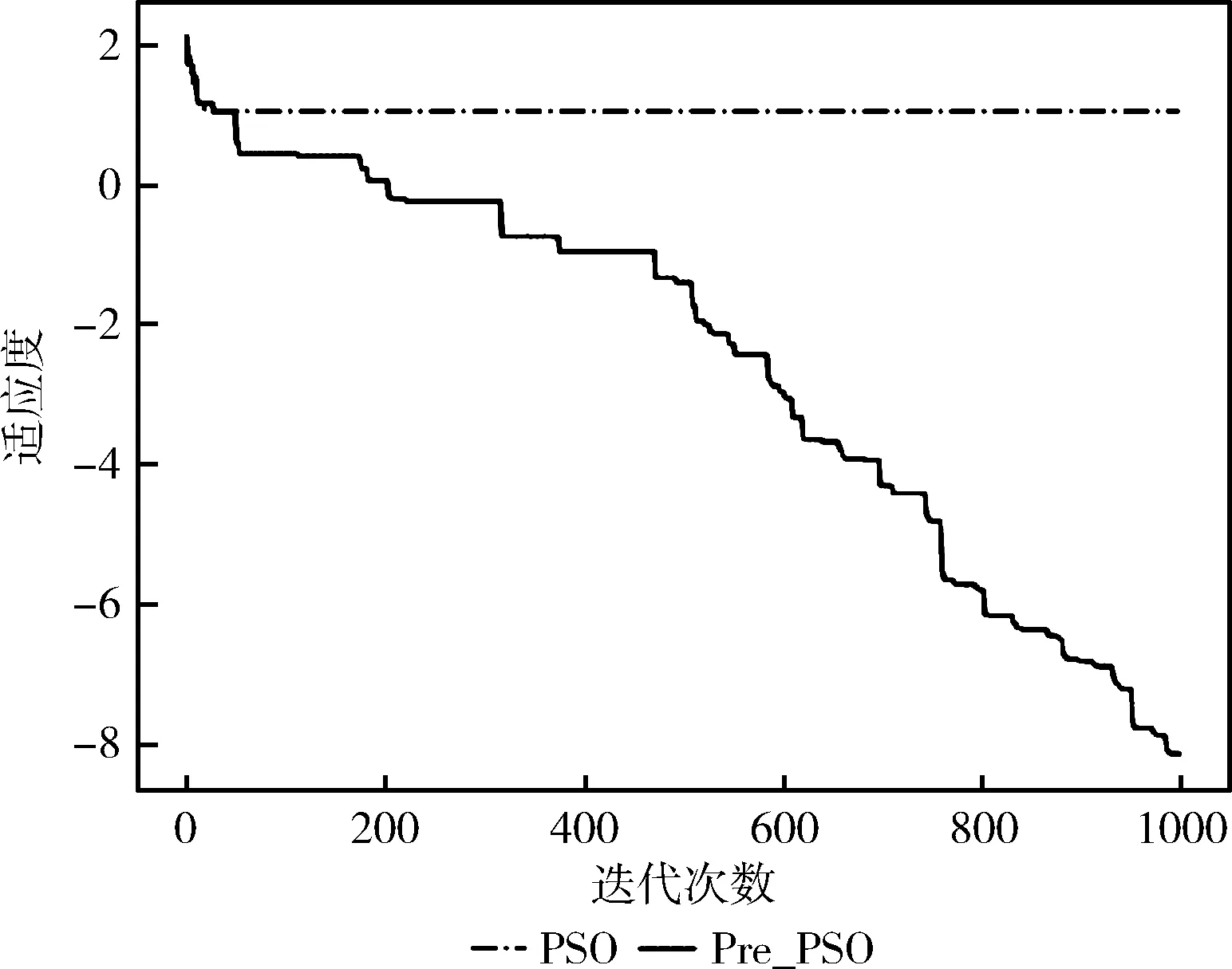
图6 算法改进寻优能力对比

由图6中曲线走势可以看出，传统的PSO算法迭代时很早陷入了局部最优解，不再具备寻优能力。而改进后的Pre_PSO算法展现了强大的跳出局部最优能力，在1000次迭代后，依然有能力继续寻找最优解。验证了改进后粒子群算法的优势。

对屯溪流域雨量水位数据进行处理后，用传统LSTM模型、未改进的PSO-LSTM模型与本文改进的Pre_PSO-LSTM模型分别对水位进行预测，3种模型的对真实值、预测值、绝对误差比情况见表1。

表1 3种模型预测结果对比

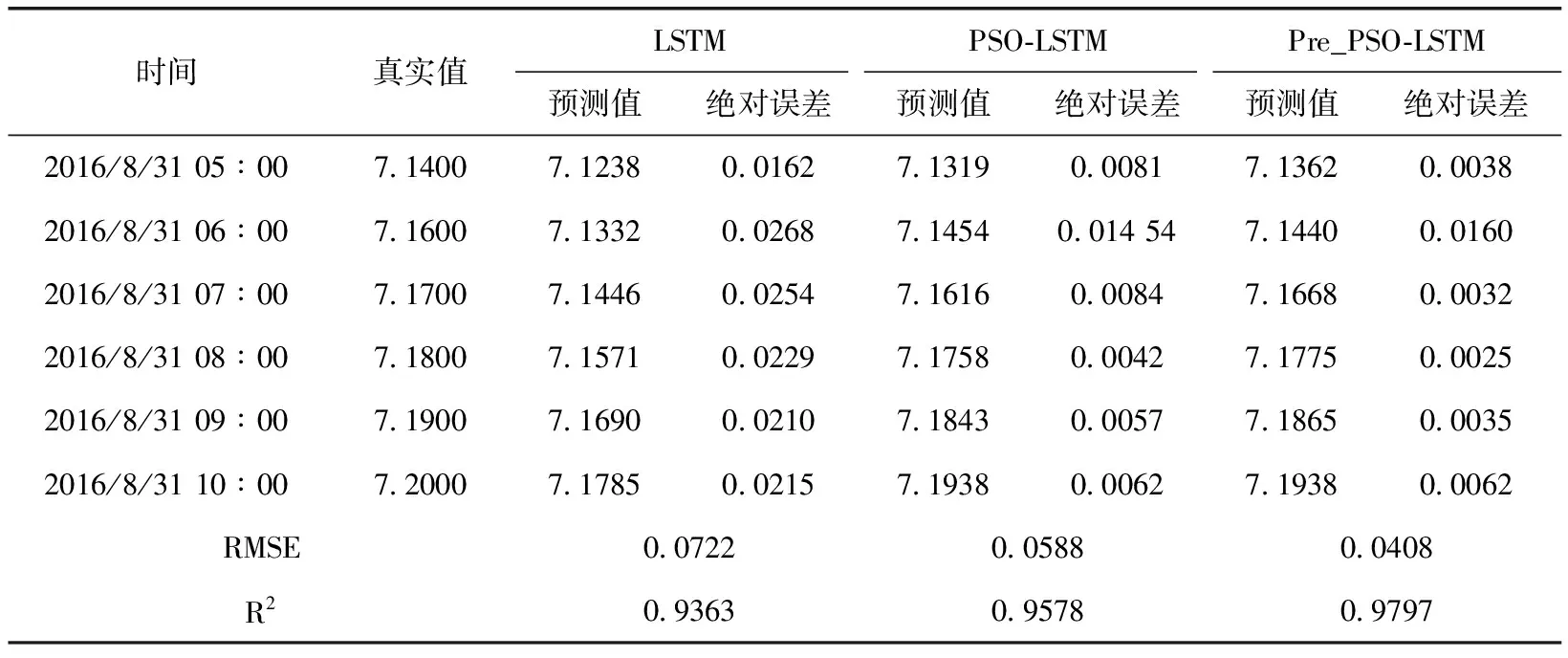
表1(续)

将PSO-LSTM与改进后的Pre_PSO-LSTM组合模型进行预测结果对比。从真实值与预测值的绝对误差可以看出，未改进的模型没有引入注意力机制，且容易陷入局部最优解，在模型预测效果上稍差。在实验条件相同的情况下，预测精度与改进后的算法相比有一定差距。

在屯溪流域数据集上，对传统BP模型、SVM模型进行训练，将几种模型训练后最好的结果进行对比实验，预测结果评价指标见表2。

表2 各模型预测效果对比

通过实验验证，BP、SVM在屯溪流域样本数据预测中表现不尽如人意，LSTM表现相对较好，符合预期的更适用于中小河流水文时间序列预测的猜想。本文在对粒子群算法进行改进并引入注意力机制与LSTM结合后，有效地提高了模型拟合效果，预测精度有一个明显提升，改进后的Pre_PSO-LSTM模型表现较为突出。

为了让实验对比结果更为直观明显，选取了测试集中部分水位变化有代表性的样本数据作为实验结果，展示真实值与预测值的对比效果。图7、图8分别为不同时间段24小时的水位变化，LSTM、PSO-LSTM、Pre_PSO-LSTM这3种模型对比实验的预测效果，结果如下。

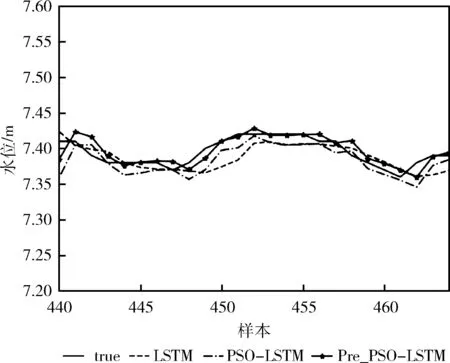
图7 各模型预测效果对比1

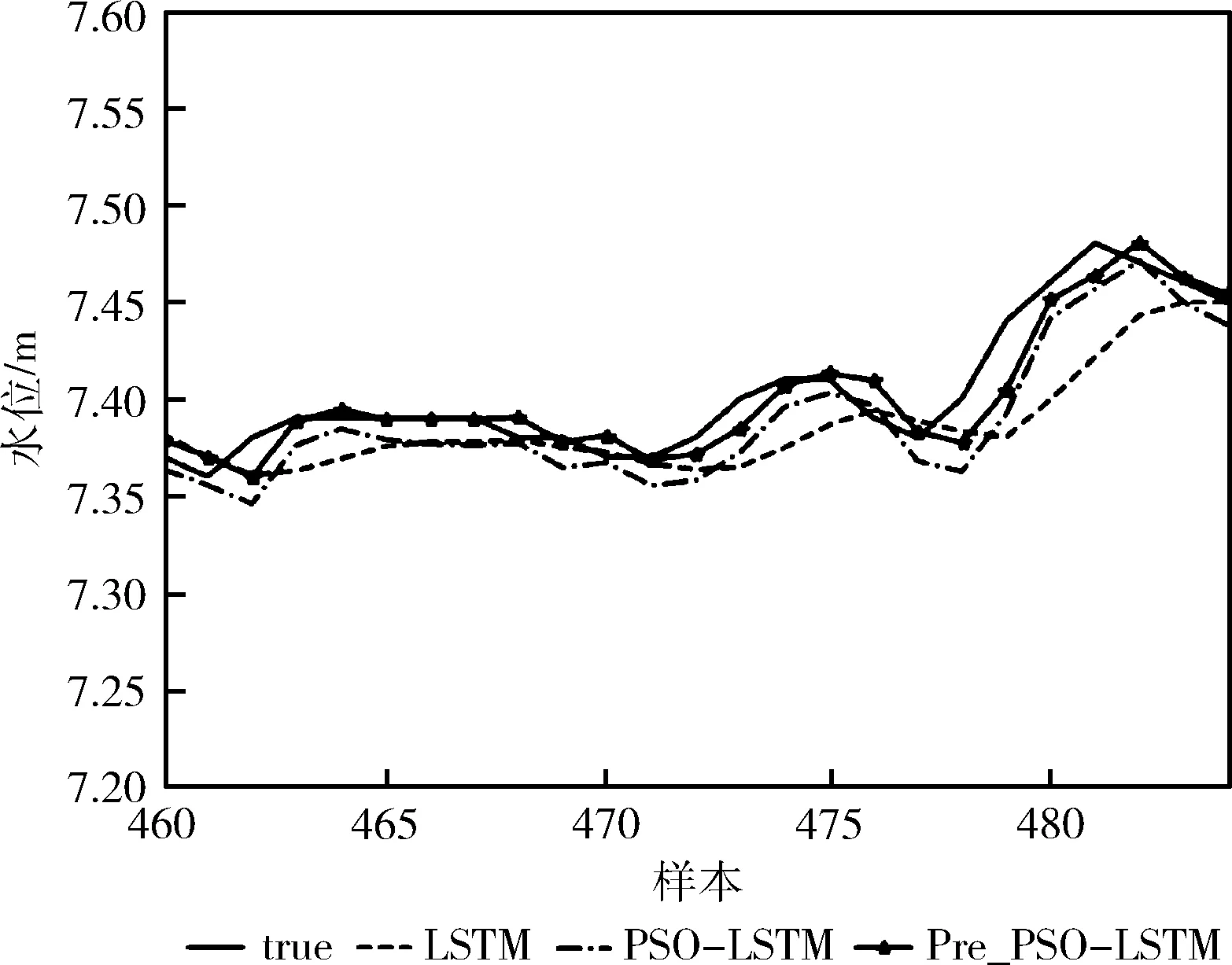
图8 各模型预测效果对比2

将该模型用于东山、漳州等中小流域进行水位预测，效果同样显著。验证该模型在中小河流水文预测方面预测效果符合预期。

4 结束语

本文提出基于改进粒子群算法，结合注意力机制优化LSTM的中小流域水文时间序列预测模型。改进后的算法与单一的优化算法相比，扩大了全局搜索能力，更能克服寻优过程中陷入局部最优的状态，并大大增加了局部寻优效率。组合模型与单一LSTM模型预测相比，能较好地解决参数选择问题，特征选择能力明显提升。通过对屯溪等流域水位数据进行应用分析。实验验证，相比于传统神经网络模型，该组合模型更加适用于复杂样本的中小流域水文时间序列的预测规律，有效提高预测准确度。