大地电磁二维并行谱元法正演计算研究*

周 翔 李长伟,2 万文武 李忠乾3

（1.桂林理工大学地球科学学院；2.广西隐伏金属矿产勘查重点实验室）

大地电磁法是一种天然源电磁勘探方法，探测深度大，被广泛应用于区域构造调查、石油勘探、地壳上地幔研究、深部找矿等领域［1-4］。随着现代技术的发展，数值模拟成为了大地电磁正演的有效手段，常见的数值模拟方法包括积分方程法、有限差分法、有限体积法等。积分方程法具有较高的求解精度，但只适用于简单模型，不适合用于复杂模型［5］。有限差分法实现简单，但是只能采用结构化网格，同样不能用于复杂模型［6］；有限体积法是基于有限差分和有限元发展起来的，兼顾了有限差分和有限元的优点，表达形式简单，适合处理带任意地形的复杂模型，但是难以实现高精度的模拟［7-8］；有限单元法网格剖分灵活，可以处理复杂模型［9-12］。

谱元法是基于有限元和谱方法发展起来的一种数值模拟方法，其优点在于一方面具有有限元处理复杂地形的能力，另一方面具有谱方法的高精度特性。

谱元法最早被Patera［13］提出，并应用于流体力学当中，同样的模型和网格下，相对其他几种方法计算量低，并且具有较高的计算精度。因为谱元法的诸多优点，国内外学者对其展开了一系列的研究。如Lim等［14］利用谱元法实现了三维腔体中电阻率正演成像。Lee［15］采用了混合阶高斯—洛巴托—勒让德（Gauss-Lobatto-Legendre，简称GLL）多项式的谱元法用于求解矢量电磁场波动方程，实现了3D谱元法的数值模拟研究。黄鑫［16］采用基于规则六面体网格谱元法进行频率域航空电磁正演。Zhou等［17］将插值节点和积分节点选在同一GLL点上，解决了有限元在低频时收敛速度慢和难以迭代求解线性方程组的问题。陈汉波等［18］基于异常场的方法，结合混合阶矢量基函数，利用不完全LU分解的IDR（s）迭代算法求解线性方程组，实现了任意各向异性介质的海洋可控源三维谱元法正演。Pasquetti等［19］将三角谱元法和四边形网格谱元法进行了对比研究，积分节点采用最优化点集Fekete节点，计算结果表明，三角网格谱元法的条件数随阶数的增长快于四边形网格谱元法。张帅胤等［20］采用一种三角形到四边形的映射，对复杂区域上椭圆形方程的混合边界问题，建立三角单元的Legendre谱元法，应用于若干不规则区域问题的计算，通过数值算例验证该方法的有效性。方小姣等［21］基于谱元法实现了大地电磁二维数值模拟。Li等［22］精确推导了关于谱元的二次多项式。赵廷刚等［23］推导了拟谱格式雪比切夫—勒让德（Chebyshev-Legendre）拟谱格式，并进行了数值实验，取得良好的效果。张荣欣等［24］用雪比切夫多项式求解了均匀流场中的声波问题。朱昌允等［25］采用Chebyshev谱元方法结合并行计算，求解三维区域的Helmholtz方程问题。刘玲［26］研究了基于高斯—洛巴托—雪比切夫（Gauss-Lobatto-Chebyshev，简称GLC）多项式谱元法的频率域三维电磁正演模拟，利用GLC正交多项式构建谱元矢量基函数，结合多项式性质，推导单元积分解析表达式，实现高精度计算。崔海洋［27］实现了基于OpenMP大地电磁二维有限元正演模拟。韩思旭等［28］实现了基于CUDA并行计算的大地电磁二维有限元数值模拟，加速比达20多倍。刘庆等［29］采用了基于CPU（OpenMP）和GPU（CUDA）异构并行处理的方式，实现了基于GPU并行的大地电磁二维正演。汪茂等［30］实现了基于大地电磁二维反演的MPI和CUDA并行算法的研究，加速比能达到2.15～3.09倍。杜伟［31］实现了基于GPU加速的直流电法的正演与大地电磁反演。谢悦等［32］研究了浓度对流扩散方程的并行计算和MATLAB的高效实现方法。苏辉等［33］研究了基于MATLAB的有限元方法的GPU加速。

本项目对大地电磁二维并行谱元法正演进行了研究。从电磁场满足的2阶偏微分方程出发得到赫姆霍兹方程，采用高阶基函数离散赫姆霍兹方程，用bicgstab求解线性方程组后得到电磁场和视电阻率的分布。为进一步提高计算速度，采用OpenMP编程模式实现了多个频点的并行计算。通过国际模型COMMEMI2D-1的计算对比，表明谱元法相较于有限元，能够采用较少网格，到达同等的精度，有效地减少了计算时间；对常见的地电模型采用并行计算，实现频点之间的并行，大大减少了正演计算的时间。

1 控制方程

大地电磁场满足如下方程：

式中，E为电场强度；D为电位移矢量，本构关系为D=εE；H为磁场强度；B为磁感应强度，本构关系为B=μH；J为电流密度，本构关系为J=σE；ρ代表电流密度，其中ε，μ，σ分别表示介电常数、磁导率、电导率。

由式（1）和B=μH可得

采用时变因子e-iωt，公式（2）可写成

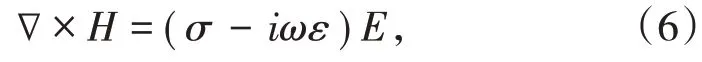
式中，ω为角频率。式（5）可写成

再对式（7）求旋度，可得到赫姆霍兹方程

采用法拉第定律H=(1/iωμ∇×E)求解磁场，并根据公式计算视电阻率

式中，Ex和Hy为电磁场的分量。

2 谱元法实现

为了用谱元法求解方程（8），将计算区域离散成四边形单元。为了方便数值积分，通过坐标映射，将离散单元转换成标准参考单元，在参考单元内利用GLL正交多项式进行数值逼近，GLL正交多项式定义在［-1，1］区间。参考单元与物理单元的转化关系见图1。

物理坐标(x,y)与参考坐标(ξ,η)之间的映射关系为

式中，mx=xe+1-xe，my=ye+1-ye为物理单元2个方向的长。

二重积分的变量替换公式为

其中，J为雅可比矩阵，

经过物理单元与参考单元的转化，将单元积分的计算转化到(ξ,η)坐标。

采用增加插值基函数阶数，或者增加剖分单元个数来提高计算精度。在谱元法中，当插值正交多项式阶数选为N=1，与传统的线性方法一致，当插值基函数阶数选为N=2，与二次插值的有限元方法一致。理论上来讲，阶数越高，效果越逼近，但同时占用内存越大，计算机消耗越多。通常4到8阶最好，为使效果最优，内存最小的情况下，本研究选择了4阶Legendre插值。

一维参考域的N阶GLL插值多项式的表达式：

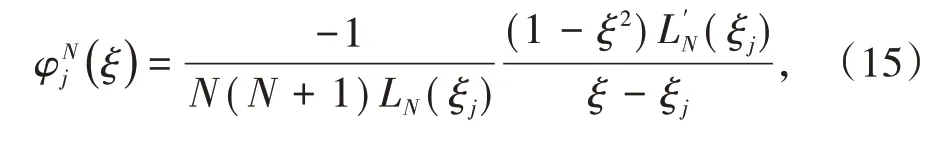
二维等参单元基函数由一阶正交多项式构成，参考单元下的基函数表达式如下。

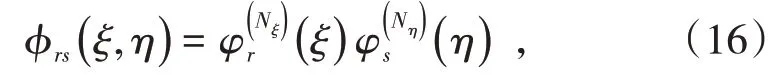
其中，ϕrs(ξ,η)是等参单元的基函数Nξ，Nη表示在参考单元ξ，η方向基函数的阶数，电场E(ξ,η)可写成

其中，Na=Nξ(Nη+1)+Nη(Nξ+1)是参考域节点数是参考域单元节点上的电场分量。

将微分方程（5）转化成积分问题，利用伽辽金残差法处理电场矢量方程，令单元内加权残差为0，即

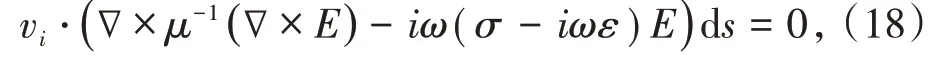
其中，vi为加权函数。

通过格林第一定律和狄利克雷边界条件n×E|∂L=0，∂L是区域的边界，式（18）可改写成

选择权函数为插值基函数ϕ͂，得到单元内的方程

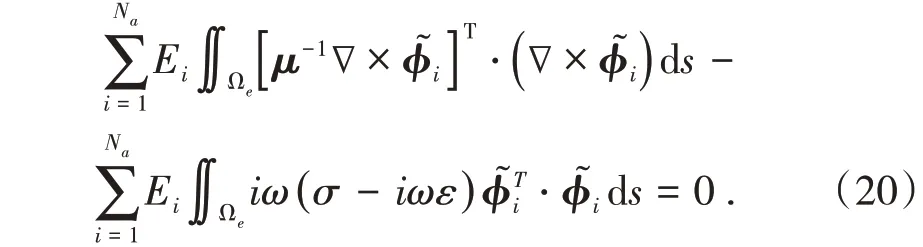
对式（20）可改写成矩阵形式

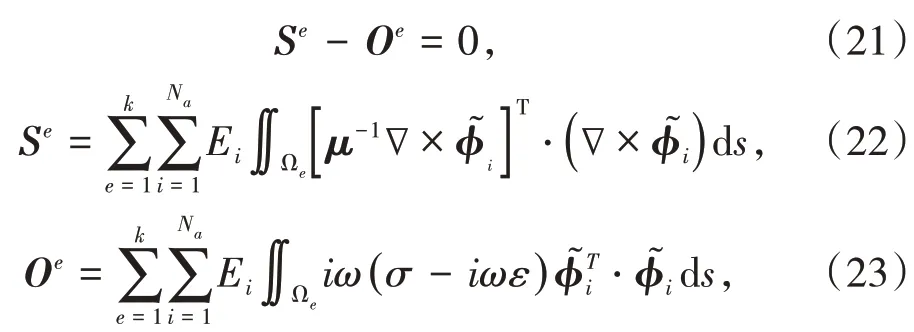
式中，Se为刚度矩阵；Oe为质量矩阵；k为单元总数。

大地电磁正演需要计算多个频点上的电磁响应，以得到地下由浅至深的电阻率变化情况。每个频点都需要进行谱元求解，为了提高计算效率，考虑了基于频点的并行计算策略。将计算任务按频点进行划分，利用OpenMP并行机制为每一个频点分配一个section，等待所有频点任务结束，将结果汇总输出。其中，并行加速比=单机的串行执行时间/N个进程的并行计算时间，并行效率=并行加速比/并行的进程个数。并行计算流程如图2所示。

3 数值计算结果与分析

基于上述分析，采用MATLAB平台编写了二维大地电磁并行谱元法的程序。

3.1 算例1

算例1采用了国际模型中COMMEMI2D-1模型对本算法进行验证，模型示意如图3所示，中间有1个低阻的异常体，低阻异常体模型位于X方向-0.5～0.5 km、Y方向0.25～2.25 km，设电阻率ρ2=0.5Ω·m，背景电阻率ρ1=100Ω·m。计算区域设置为X方向从-10～10 km，Y方向为0～4 km。采用谱元法计算得到的视电阻曲线如图4所示，可以看出，计算结果与IE方法的计算结果相吻合，最大误差不超过5%。

在本算例中，将本方法与有限元进行对比，如表1所示。谱元采用20乘20的网格，有限单元法采用60×80的网格，二者到达了相同的精度。在同等精度下，SEM相较于FEM剖分更少的网格、用了更少的计算时间。

?

3.2 算例2

算例2为地堑模型（图5），地堑电阻率ρ2=100Ω·m，在地堑上面有1层覆盖层，电阻率ρ1=10Ω·m。设置空气层电阻率为1010Ω·m，凹陷部分为1个倒梯形，梯形上边长为4 km，梯形下边长为2 km，梯形高为2 km。在频率范围0.01～1 Hz内进行正演计算，绘制了X方向-3～3 km等值线图。地堑视电阻率等值线见图6。从视电阻率图可以看出，地堑轮廓较为明显，很好地反映了轮廓的边界，其低阻异常的范围能够反映模型的基本特征，这与正演所设定的地电模型完全吻合。地堑的结果进一步验证了本算法的正确性。

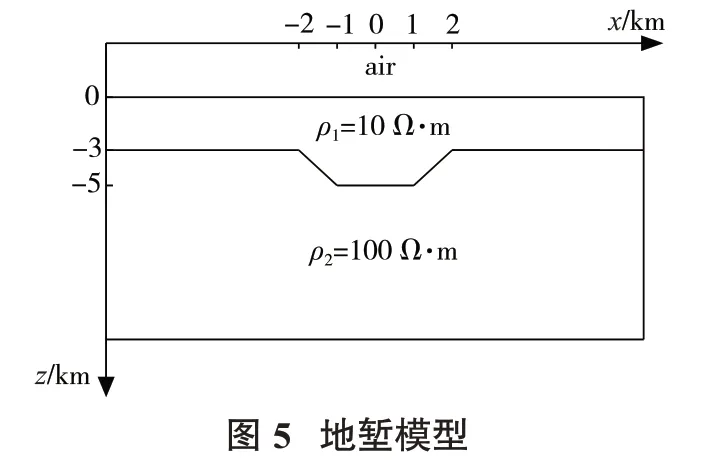
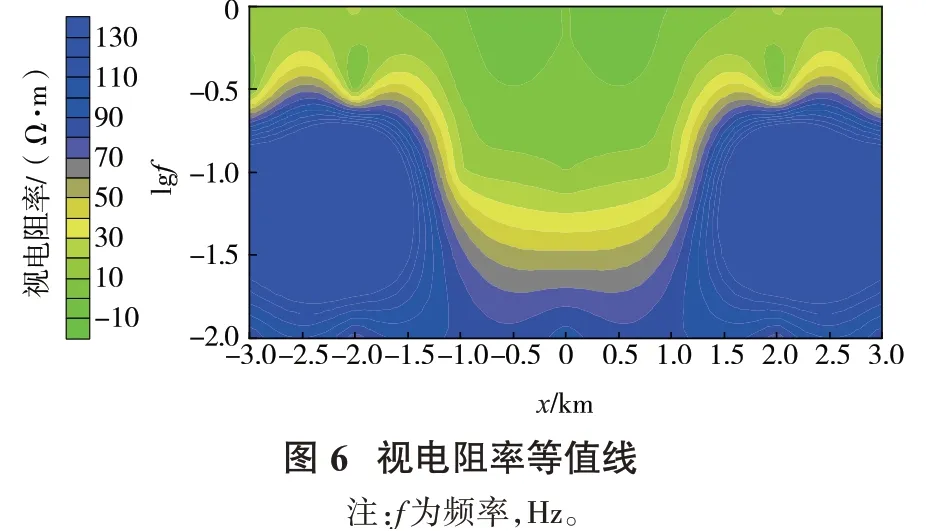
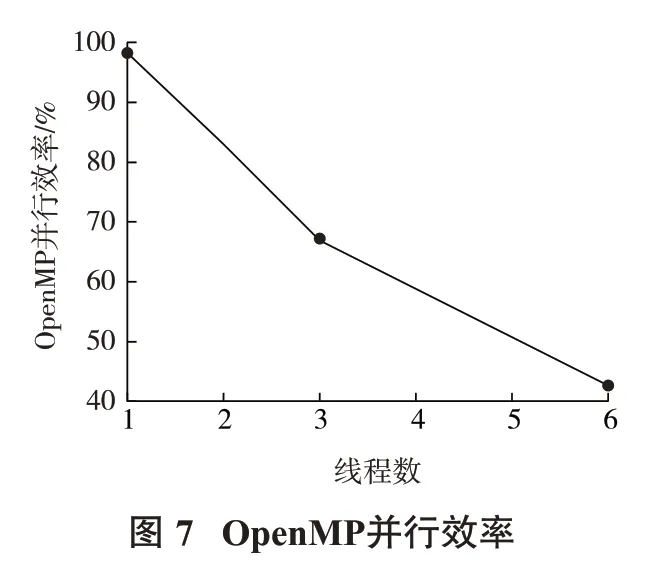
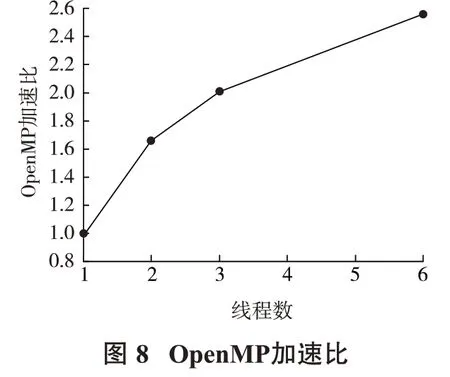
表2为多个频率情况下地堑模型串并行计算时间对比。与串行相比，并行更慢的原因是程序需要花费时间在并行管理，单个线程没有体现并行的意义。2个线程的加速比为1.659 8倍，当采用6个线程的时候，加速比可以达到2.561 1倍。图7是OpenMP并行效率，可以看出，随着线程数的增加，加速比增加，计算时间减少，但是加速比与线程数不是同比例增加（图8），即并行效率降低了，这是因为随着线程数的增加，线程之间的通讯量和并行管理开销增加。

?

4 结论

将谱元法应用于大地电磁二维正演，开发了算法程序，通过数值模拟进行测试。国际模型COMMEMI2D-1验证了算法的有效性和准确性，与有限元对比，谱元法在同等精度下只需剖分更少的网格，用更少的计算时间；利用地电模型测试OpenMP并行效果，基于频点的并行策略能大大提高正演速度，可以为反演的快速实现奠定基础。