基于SSAE-SVM的滚动轴承故障诊断方法研究

徐先峰，黄 坤，邹浩泉，赵龙龙

(长安大学电子与控制工程学院，陕西 西安 710064)

0 引言

滚动轴承是广泛应用于旋转机械设备的核心器件，一旦发生故障，将对机械系统、工人生命安全和国民经济构成严重威胁。因此，对滚动轴承故障的精确诊断具有现实意义[1-3]。进入21世纪以来，深度学习和人工神经网络在滚动轴承故障诊断分类领域展现出巨大潜力。研究人员将多种具备监督学习能力的深度学习算法应用于轴承故障诊断中[4]。Feng等[5]为提高传统轴承故障诊断的有效性，提出了基于改进的量子人工蜂群算法的反向传播神经网络诊断模型(improved quantum artificial bee colony-back propagation,IQABC-BP)，利用改进的量子蜂群算法进行量子蜂群计算，并解决了利用率低的问题。应用改进的量子蜂群算法对反向传播(back propagation,BP)神经网络的初始权重、阈值和隐层数进行优化，并将其应用于滚动轴承的故障诊断。试验结果表明，IQABC-BP的收敛速度更快、故障诊断效果更好。然而，该方法并未考虑频域的滚动轴承故障信号分析。为了在频域分析滚动轴承故障特征，Liang等[6]提出了1种基于卷积神经网络(convolutional neural network,CNN)和频谱图的滚动轴承故障诊断方法。该方法利用快速傅里叶变换(fast Fourier transform,FFT)，从原始一维振动信号中提取频率特征，并将其转换为二维频率频谱图输入到CNN模型中，以实现滚动轴承的故障诊断。试验结果表明，与传统方法相比，该方法具有更优良的精度和稳定性。但是，该方法在解决标签数据有限的无监督或者半监督学习问题上存在很大的局限性。李萌等[7]针对标签数据有限的滚动轴承故障诊断问题，提出了基于堆栈稀疏自编码(stacked sparse autoencoder,SSAE)的滚动轴承故障诊断方法。该方法利用SSAE网络对原始信号进行特征提取，并利用Softmax分类器进行分类，实现滚动轴承故障诊断。试验结果表明，该方法对解决无监督学习问题具有明显优势。

综合分析深度学习模型在滚动轴承故障诊断领域的应用现状，主流的故障诊断方法仍然是基于监督学习的应用，即利用有标签的数据来训练模型。但是，现实中所获得的数据集中，大部分为无标签数据。如果要制作数据标签，不仅费时费力，而且具有很大的随机误差。

本文在上述研究的基础上，提出了1种基于SSAE和支持向量机(support vector machine,SVM)的堆栈稀疏自编码-支持向量机(stacked sparse autoencoder-support vector machine,SSAE-SVM)的滚动轴承故障诊断方法。该方法在SSAE自适应特征学习网络中加入贪婪算法逐层进行训练，并使用反向微调算法实现误差最小化，进而对滚动轴承故障频域特征进行深层学习。最后，把5层结构的SSAE特征学习网络的输出输入到SVM分类器中，以实现滚动轴承故障的准确分类。

1 基于SSAE的滚动轴承深层故障特征提取

1.1 堆栈稀疏自动编码器原理

自动编码器(autoencoder,AE)采用典型的对称无监督学习算法，通过反向微调算法最小化目标和输出误差[8]。AE结构包含输入层、编码层和输出层3级网络。AE结构如图1所示。

图1 AE结构图Fig.1 Structure diagram of AE

稀疏自动编码器(sparse autoencoder,SAE)是在AE的基础上增加了一些稀疏性约束，用于寻找一组超完备基向量，以便高效地表示样本数据[9]。由于对隐藏层进行了稀疏性限制，SAE的学习能力得到了显著增强，可以获得更为简单的信号表达方式。因此，该方法更容易获取信号中的信息，以便对信号进行压缩、编码等加工处理。

SSAE是由多层稀疏自编码器组成的神经网络模型。SSAE网络结构如图2所示。

图2 SSAE网络结构Fig.2 Structure of SSAE network

图2中：X为输入向量；Si为第i个(i=1,2,...,n)稀疏自动编码器；hi为Si的输出特征向量。

SSAE与自动编码器类似，前向和反向训练模式可以减小重构信号和输入信号之间的偏差。将高维输入数据转换为低维特征，并经过解码过程中激活函数的重构成为输出目标。编码层输出的编码向量可以被视为对原始输入信号的一种深层特征提取[10]。

①编码过程：通过激活函数fθ()将样本映射为编码向量，如式(1)所示。

Y=fθ(WX+b)

(1)

式中：fθ()为Sigmoid激活函数；W为输入层到隐含层的权值矩阵；b为隐含层阈值(偏置)向量。

②解码过程：原始数据的矢量重构过程如式(2)所示。

Z=fθ(WTY+b′)

(2)

式中：WT为隐含层到输出层的权值矩阵；b′为输出层阈值(偏置)向量。

1.2 基于SSAE的滚动轴承深层故障特征提取

SSAE网络的训练过程包含前向网络预训练(无监督方式)和反向微调(有监督方式)2个过程。网络的训练过程中，输入特征信号通过正向传播和反向传播2个阶段循环地调整各层的参数，以提高神经网络的性能。SSAE前向网络预训练采用了贪婪算法[11]进行逐层训练。贪婪算法逐层训练过程如图3所示。

图3 贪婪算法逐层训练过程Fig.3 Layer-wise training process of greedy algorithm

由图3可知，该算法训练过程如下。首先，利用输入的原始滚动轴承故障特征训练SSAE神经网络的第一层稀疏自编码器，得到参数权重W(1)和偏置b(1)。然后，在第一层网络训练结束之后，开始训练第二层具有2个隐含层的网络；将第一个SAE隐含层的输出作为第二个SAE隐含层的输入，得到第二层的参数权重W(2)和偏置b(2)。以此类推，把已训练好的第(n-1)层的输出作为第n层的输入，获得最后一层的参数权重W(n)和偏置b(n)。

SSAE的训练过程可理解为调整其参数权重矩阵W和偏置b，使原始输入与重构误差的损失函数最小化。当重构目标与训练样本的相似度达到最高时，编码矢量特征向量可被视为原始信号的最优降维表达。其数学表达式为：

(3)

式中：xi为第i个神经元对应的输入向量；zi为第i个神经元对应的输出向量；l为神经元个数。

在反向微调过程中，采用BP算法优化和更新所有隐含层参数，以增强整个网络的性能。部分训练数据被选作整个网络的监督学习的输入。误差信号流反向传播流程如图4所示。

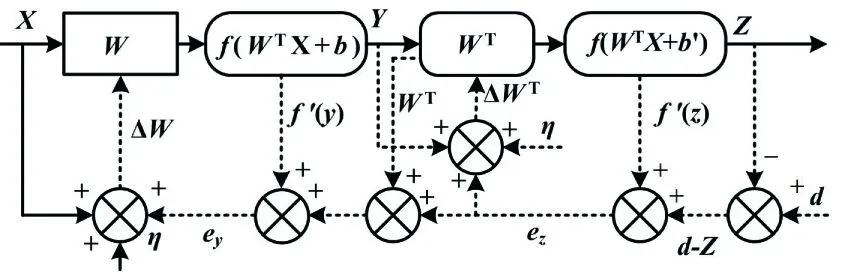
图4 误差信号流反向传播流程Fig.4 Process of error signal flow back propagation

图4中：ez和ey分别为输出层和隐含层的误差信号；η为学习率；ΔWT和ΔW分别为隐含层和输入层的调整权值；f为各层的转移函数，具有连续可导的特性；d为期望的误差。

利用式(1)和式(2)，将BP误差展开到输入层：

(4)

(5)

通过梯度下降法进行更新，取得合适的权值和偏置参数，使误差E最小。对输出层的权值参数进行调整：

(6)

式中：η为学习率。

反向对隐含层的权值进行调整：

(7)

2 SVM分类器及构造方法

SVM是1种以统计学原理作为理论基础的监督学习方法，具有构造简单、结构风险小、非线性问题处理能力佳、泛化性能好等优点，在处理模式识别及回归问题中展示了良好的性能[12]。本文选择径向基核函数作为SVM滚动轴承故障分类器的核函数，处理非线性问题。核函数表达式为：

(8)

SVM算法原来是专门针对二值分类问题所研究的。然而，要识别的滚动轴承故障类型远不止2种。对此，解决方法是训练多个二分类器来模拟多分类器。多分类器的构造方法主要有直接法和间接法。经过SSAE深层特征提取器提取的特征在SVM分类器中进行分类。SVM分类器原理如图5所示。

图5 SVM分类器原理示意图Fig.5 Schematic diagram of SVM classifier

3 SSAE-SVM滚动轴承故障诊断模型

3.1 模型框架构建流程

SSAE-SVM滚动轴承故障诊断模型简称为SSAE-SVM模型。SSAE-SVM模型整体设计流程如图6所示。

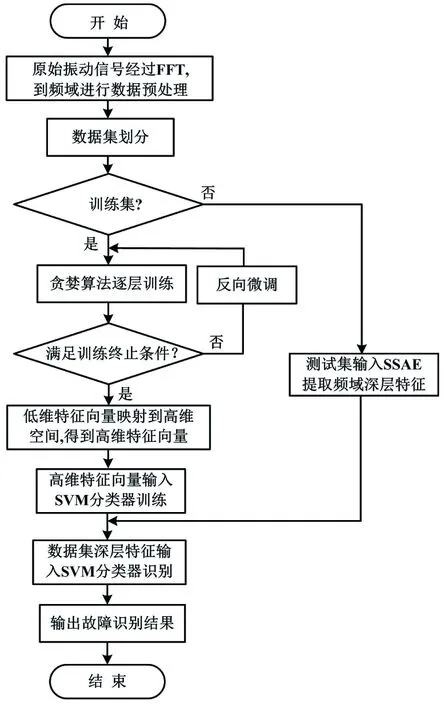
图6 SSAE-SVM模型整体设计流程Fig.6 Overall design process of SSAE-SVM model

模型搭建流程主要包含数据处理、基于SSAE的滚动轴承故障特征自适应学习和基于SVM分类器的滚动轴承故障分类这3个核心内容。

在模型的搭建过程中，激活函数fθ(z)选择tanh激活函数，即：

(9)

式中：θ={W,b}为参数集合。

当fθ(z)接近1时，表示神经元活跃；当fθ(z)接近-1时，表示神经元被抑制。

3.2 试验验证

本文的试验数据来自美国凯斯西储大学滚动轴承数据中心。其数据集是学术界普遍使用的轴承故障诊断基准数据集[13]。美国凯斯西储大学滚动轴承数据集采集系统主要包括风扇端轴承SKF6203、1.5 kW的电机、驱动端轴承SKF6205扭矩传感器和编码器等部件。本文选用美国凯斯西储大学滚动轴承驱动端和风扇端轴承数据作为试验数据，检验所建立的SSAE-SVM模型的性能。该试验所用数据为48 kHz的驱动端轴承SKF6205数据：选择10 000个数据样本，按照7∶3的比例设置训练集和测试集样本数量[14]。

试验数据样本划分如表1所示。

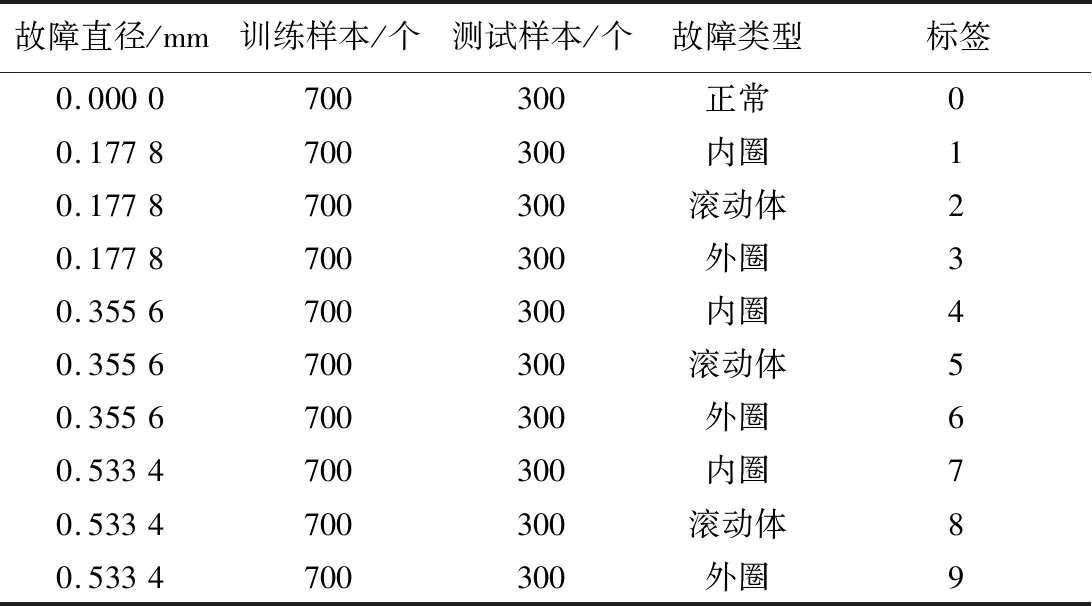
表1 试验数据样本划分Tab.1 Division of experimental data samples

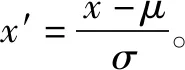
①模型训练的收敛速度和准确率。

利用训练样本，检验SSAE-SVM模型与对比模型在7 000个训练集样本上的准确率和收敛速度。根据第5次、第10次、第20次、第30次、第50次、第80次、第100次、第120次、第150次迭代所对应的准确率，绘制准确率折线。不同训练次数的模型准确率对比如表2所示。

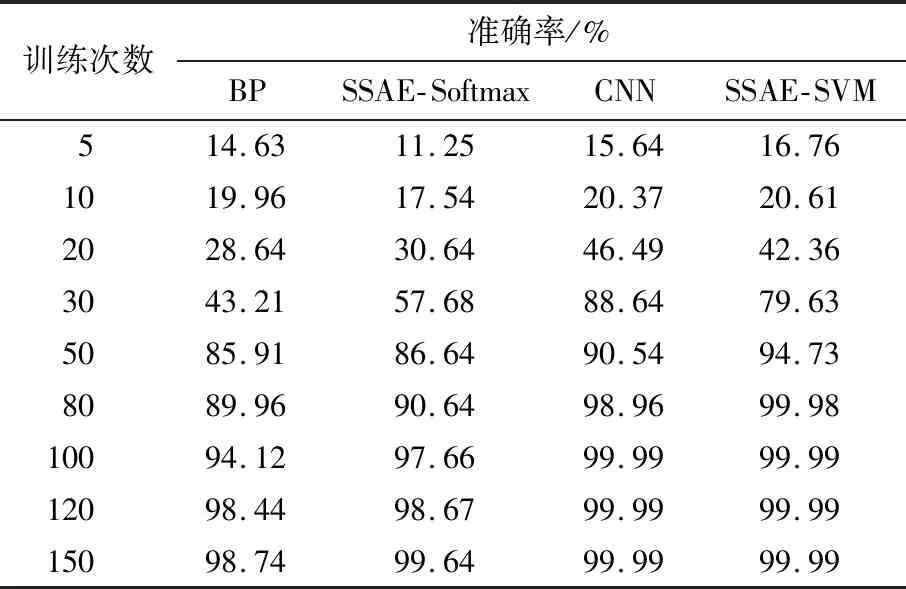
表2 不同训练次数的模型准确率对比Tab.2 Comparison of model accuracy with different training times

由表2可知：SSAE-SVM模型和CNN模型的收敛速度比SSAE-Softmax模型和BP模型更快；SSAE-SVM模型的准确率在训练次数达到80次后稳定在99.9%以上。

②SSAE-SVM模型和对比模型的性能对比。

SSAE-SVM模型与3个对比模型使用测试集分别试验10次。不同测试次数的模型准确率对比如图7所示。

图7 不同测试次数的模型准确率对比Fig.7 Comparison of model accuracy with different test times

由图7可知，SSAE-SVM模型比SSAE-Softmax模型、BP模型和CNN模型的滚动轴承故障诊断准确率更高，平均准确率可达99.74%。

③迭代次数对模型准确率的影响。

为了检验迭代次数对滚动轴承故障诊断性能的影响，将迭代次数分别设置为5次、10次、20次、50次、100次，利用测试集进行10次试验，然后取平均值。不同迭代次数的模型准确率对比如图8所示。

图8 不同迭代次数的模型准确率对比Fig.8 Comparison of model accuracy with different iteration times

由图8可知，所有模型的滚动轴承故障诊断的准确率均受到了迭代次数的影响。尤其当迭代次数小于10时，3个对比模型的故障诊断准确率均有较大的损失。BP模型在迭代次数大于50后才达到90%左右。CNN模型在处理大量有监督学习训练样本时具有很高的准确率，但在少量有监督学习样本中的性能较差。相较于3个对比模型，SSAE-SVM模型准确率更高、稳定性更强，因而更具优越性。

4 结论

本文基于无监督学习方法，提出了基于SSAE-SVM的滚动轴承故障诊断方法，解决了现有算法过度依赖有标签故障数据的问题。首先，利用SSAE进行无监督式深层学习获得滚动轴承故障的高维深层特征，构建5层SAE堆叠而成的SSAE自适应学习网络。然后，使用贪婪算法逐层训练和反向微调算法对其进行改进。最后，将深层特征向量输出至SVM监督学习分类器，实现滚动轴承故障分类。采用美国凯斯西储大学滚动轴承数据集将SSAE-SVM滚动轴承故障诊断模型分别与SSAE-Softmax的轴承故障诊断模型、基于BP神经网络的轴承故障诊断模型和基于CNN神经网络的滚动轴承故障诊断模型进行对比试验。试验结果表明，本文所提模型的准确率更高、收敛速度更快，表明应用无监督学习建立轴承故障诊断模型将成为轴承故障诊断的重要发展方向之一。