欠驱动桥式吊车系统的非线性扩张状态观测器设计
2022-02-14张桐松邵雪卷张井岗赵志诚陈志梅
张桐松,邵雪卷,张井岗,赵志诚,陈志梅
(太原科技大学电子信息工程学院,山西 太原 030024)
0 引言
桥式吊车属于典型的非线性欠驱动设备,被广泛应用于工业、港口、建筑工地、露天仓库等场合,执行货物的运输。对于桥式吊车系统的定位防摆控制,一般采用状态反馈的方法实现[1-4]。其状态信息通常经过传感器直接测量得到。但在实际工作现场,吊车系统的小车速度及摆角速度等信号不容易直接测量。即使可测,也掺杂着大量的噪声,且安装速度传感器也会增加硬件的成本。
为了解决桥式吊车状态信息难以测量的问题,国内外学者进行了一系列研究。崔建伟等[5]和钟斌等[6]针对实际工程中摆角与摆角角速度信息难以测量的问题,利用小车位置信息设计了全维线性状态观测器。曾少航等[7]针对吊车吊重系统设计了降维观测器,用可测的小车位移和速度信息估计出摆角与摆角角速度信息。以上文献均基于线性化模型构建观测器。一旦系统状态远离平衡点,所设计的观测器便会失效。因此,根据非线性模型设计状态观测器更符合工程实际需要。
钟斌等[8]利用神经网络能对任意函数逼近的原理,以吊重摆角变量作为可测输入,设计了神经网络观测器。杜鹏等[9]以摆角信息作为可测输入量,针对吊车吊重摆角子系统,设计了非线性扩张状态观测器。但这两种方法没有同时观测小车的位置与速度信息。为此,Feng等[10]和钟斌等[11]以小车位置信息为输入,分别设计了不同形式的扩张状态观测器,成功估计了吊车系统的状态。
以上文献都是桥式吊车在定绳长情况下观测器的构建问题。在工程实际中,当小车水平运动和负载升降同时进行时,上述方法的状态估计偏差渐近收敛时间都会增大,甚至有可能发散。为了解决这个问题,本文给出了一种桥式吊车系统在绳长变化时非线性扩张状态观测器的设计方法,用于重构桥式吊车系统的状态。仿真结果证明了该观测器的可行性和有效性。
1 模型描述
实际桥式吊车系统比较复杂。一般假设吊车系统满足以下条件。
①钢丝吊绳质量相对于负载质量可以忽略不计,吊绳的刚度足够大。
②负载只在二维平面内运动,且被看成一个无体积的质点。
③小车和地面之间的摩擦力与速度成正比。
④忽略小车与吊绳连接处的摩擦力。
二维桥式吊车系统物理模型如图1所示。
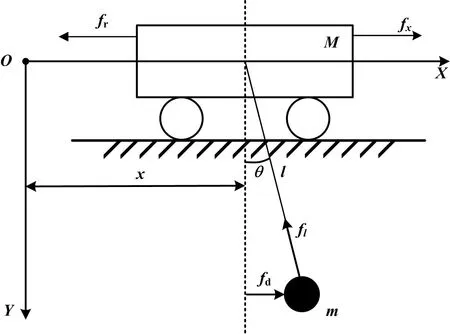
图1 二维桥式吊车系统物理模型Fig.1 Physical model of two-dimensional overhead crane system
图1中:M为桥吊系统的小车质量;小车在驱动电机的水平驱动力fx的作用下沿X轴方向运动;fr为小车运动时所受的摩擦力;μ为摩擦系数;fd为小车所受到的外部干扰;m为负载质量;负载在升降电机的驱动力fl的作用下沿Y轴方向运动;l为吊绳长度,负载通过吊绳与小车相连;小车在运动的过程中会造成负载摆动,摆角幅度用θ表示。
由拉格朗日方程可得含有扰动的二维变绳长桥式吊车系统动力学模型,为:
(1)
将q=[xlθ]T选作广义坐标向量,则可将式(1)表示为以下矩阵形式:
(2)

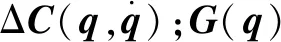
标称值矩阵为:
(3)
(4)
G0(q)=[0 -mgcosθmglsinθ]T
(5)
控制向量为:
U=[fxfl0]T
(6)
外部干扰向量为:

(7)
式(2)可进一步改写为:
(8)

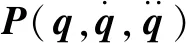

(9)
2 扩张状态观测器的设计

(10)
基于式(10)的非线性扩张状态观测器设计为:

(11)
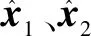
式(11)的非线性函数定义为:
(12)
其中:
(13)
式中:E1i为估计误差向量e1的第i个分量,E11为小车位置的估计误差,E12为吊绳长度的估计误差,E13为负载摆角的估计误差,0<α<1。
假设:总扰动D(t)及其导数h(t)都是有界的。
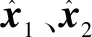

(14)
在参数满足一定条件的情况下,扩张状态观测器的输出量将在有限时间收敛至实际状态的邻域内。关于扩张状态观测器的收敛性证明,详见文献[12]中的推论2.1。

(15)
如果|E1i|≤1、|E2i|≤1、|E3i|≤1,则估计误差可以表示为:
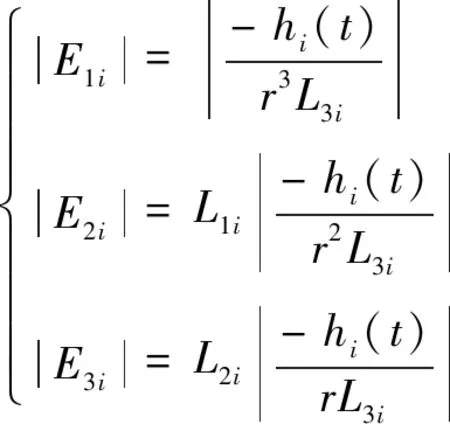
(16)
如果|E1i|>1、|E2i|>1、|E3i|>1,则估计误差可以表示为:

(17)
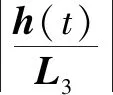
3 仿真研究
为了验证本文方法的可行性,在Matlab/Simulink中对所设计的非线性扩张状态观测器进行仿真,并与线性扩张状态观测器的估计效果进行比较。
桥吊模型的相关仿真参数如下:小车质量M=6.16 kg,负载质量m=1 kg,重力加速度g=9.81 m/s2,摩擦力系数μ=20.37。为了保证扩张状态观测器的渐近稳定性,观测器增益取L1=L2=L3=diag[3 3 1],非线性函数的参数α1=α=0.7、α2=0.4、α3=0.1、r=70。小车驱动力fx=1 N。吊绳驱动力fl=1 N。系统的初始状态设计为(0,0.4,1.7,0,0,0)。扩张状态观测器的初始状态为(0,0,0,0,0,0)。系统内部的参数摄动是通过增加桥吊模型参数值的10%来实现的。桥吊系统受到的慢时变外部干扰fd取值为:
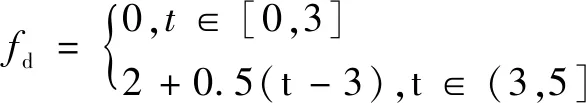
(18)
图2给出了非线性扩张状态观测器在慢时变扰动下,系统状态的非线性估计曲线及误差曲线。图2中,系统状态的实际值曲线用黑色实线表示,估计曲线用黑色虚线表示,误差曲线用黑色点划线表示。
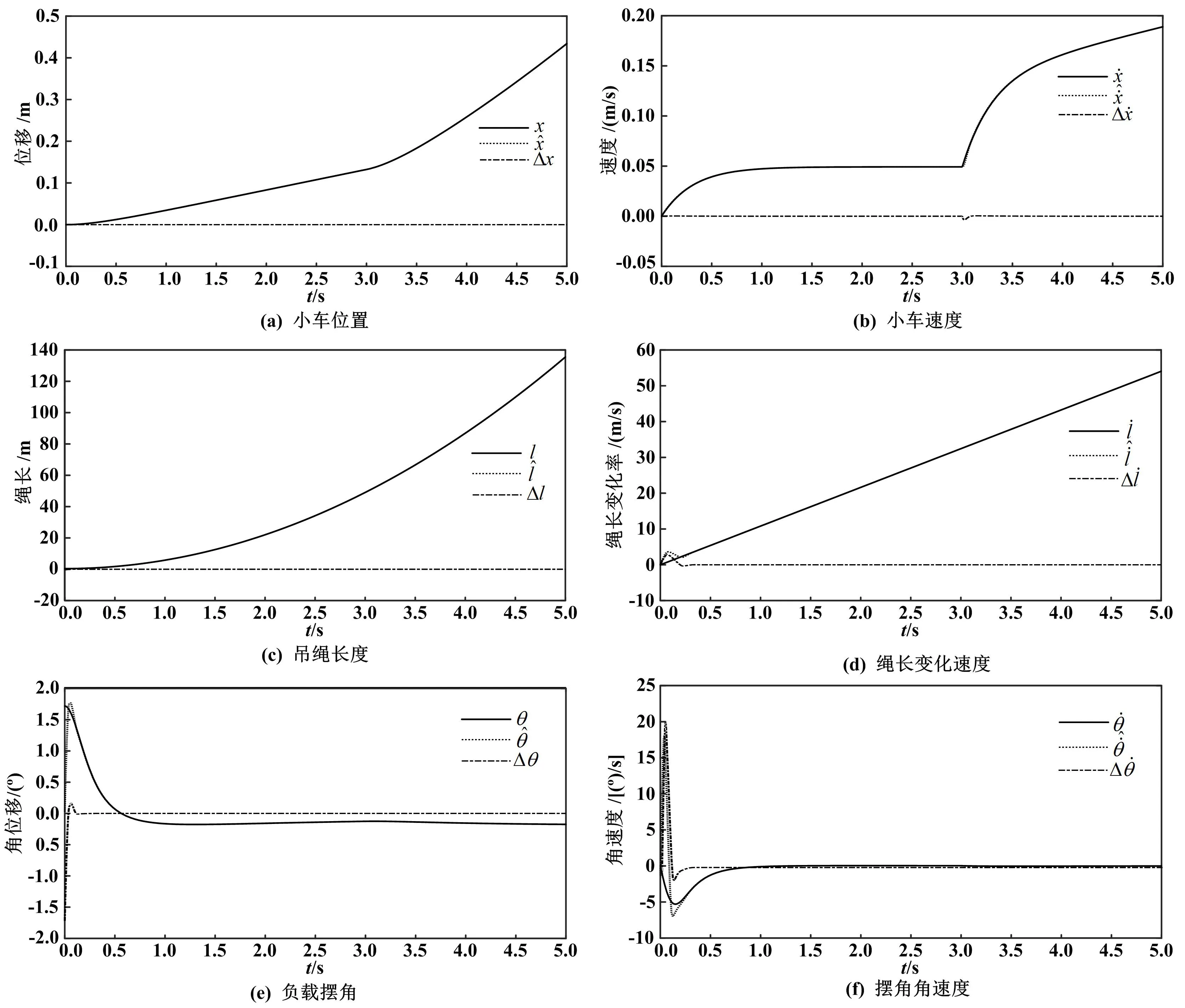
图2 系统状态的非线性估计曲线及误差曲线Fig.2 Nonlinear estimation curves and error curves of system state

为了进一步说明本文所给出的非线性扩张状态观测器的有效性,下面给出线性扩张状态观测器的仿真结果。用于观测桥吊系统(8)状态的线性扩张状态观测器设计为:
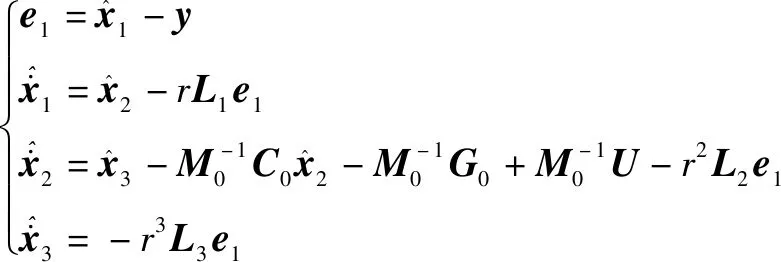
(19)
线性扩张观测器(19)选取与非线性扩张观测器(11)相同的参数值。
系统状态的线性估计曲线及误差曲线如图3所示。
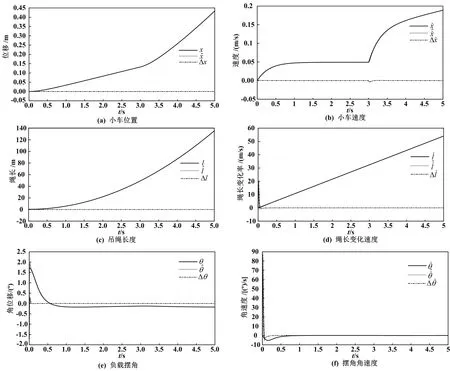
图3 系统状态的线性估计曲线及误差曲线Fig.3 Linear estimation curves and error curves of system state
将图2(a)、图2(b)、图2(c)、图2(e)与图3(a)、图3(b)、图3(c)、图3(e)进行对比,可以发现非线性扩张状态观测器的线性部分与线性扩张状态观测器的仿真结果基本相同。从图2(d)和图3(d)的比较中可以看出,在绳长变化速度上,非线性扩张状态观测器的估计值超调量明显小于线性扩张状态观测器的。对于摆角角速度的估计,图2(f)的估计峰值不超过19°/s,而图3(f)的角速度估计峰值接近87°/s,且可从其误差曲线观察到轻微振荡,说明非线性扩张状态观测器的估计效果优于线性扩张状态观测器。尽管线性扩张状态观测器的收敛时间短,即快速性优于非线性扩张观测器,但它的估计峰值过高,使用到控制器中会产生更为不利的影响。综合来说,所设计的非线性扩张状态观测器更能满足实际需求。
4 结论
本文利用小车位置和负载摆角等测量信息设计非线性扩张状态观测器,合理选取观测器参数,使观测器能以有限时间和微小误差对桥吊系统的状态进行实时估计,从而解决了吊绳绳长变化时状态收敛时间长以及扰动估计偏差大的问题。在相同条件下,非线性扩张状态观测器的收敛过程更为平缓,没有出现高频的振荡,估计性能和抗扰性能也比线性扩张状态观测器更为实用。仿真结果表明,桥吊系统状态在0.3 s内可得到准确估计值,观测器设计合理且有效。
