智能网联环境下高速公路匝道合流区域协同控制

2022-02-14聂振宇马庆禄孔国英

兰州交通大学学报 2022年1期

蔡科，聂振宇，马庆禄*，孔国英

(1.重庆交通大学交通运输学院，重庆 400074；2.重庆城市交通开发投资(集团)有限公司，重庆 401120；3.重庆奉建高速公路有限公司，重庆 401120)

匝道合流区域是主线车道与匝道的交汇路段，包括匝道、加速车道以及与之相连接的主线车道部分[1].由于匝道和主线车辆在此区域合流汇入，交通量在时间和空间上突然增大，极易导致交通流速度降低甚至出现混乱等问题，匝道合流区域不仅是高速公路通行能力的瓶颈，也是交通事故多发的路段[2].因此，提高高速公路匝道合流区域的通行效率是保障路网运行通畅的关键.

针对匝道车辆汇入与主线车辆冲突的研究，解决方法主要分为两类：匝道信号控制[3]和区域协同控制[4].Lim等[5]以匝道和连接的主线下游路段延误量最小为控制目标，用交通流量、合流区域长度和长度建立控制模型，利用线性规划方法求解满足模型约束条件的最优解制定最佳的信号控制方案，在饱和交通流量下该模型降低了路网整体的行程时间和延误时间.Chiang等[6]提出一种匝道与主线流量预测的动态控制方法，利用传感器实时感知主线车流的运行状态，在保证主线通行效率的同时对匝道车辆进行控制，只有主线车流量较大形成排队才对主线和匝道车辆同时进行信号控制.Chen等[7]针对不同车道提出一种主线与匝道车辆行程时间的均衡控制模型，以路网通行效率最大为控制目标，根据主线和匝道不同的控制策略构建平衡机制，实现路线行程时间和延误时间减少.刘畅等[8]考虑的通行效率和行车舒适性构造目标函数，基于先进先出的合流次序，动态计算相邻车辆通过合流点的时间差，利用庞特里亚金极小值原理求解车辆最优行驶策略.马庆禄等[9]引入博弈论原理协调控制车辆，考虑安全和行驶效率因素构建博弈收益阵列，根据纳什均衡消解车辆间通行权冲突问题.Zhang等[10]在保障获取精确的主线车流信息下，充分利用匝道车辆占有率，采用多层优先级控制方案，实现主线与匝道车辆通行效率均衡，减少路网拥堵.传统的匝道控制研究主要是通过对匝道车辆汇入前的速度调节，在不影响主线通行效率的前提下完成汇入[11].由于缺乏精确的车辆运行状态和道路的感知手段，该类方法很难实现各个车辆的协同控制[12].近年来物联网和5G通讯技术的发展，车辆间和车辆与道路设施协同工作的技术日益成熟，对单个车辆的精准控制成为了可能，高速公路匝道合流区域车辆协同控制研究有了新内容[13-14].

智能网联环境下考虑车辆博弈收益函数时往往赋予安全因素较大的权重，安全因素又是车辆间隙和行驶速度的函数，这样的研究思路可能会产生不切合实际的纳什均衡状态[15].而匝道与主线车辆的换道动机不同，本文增加了匝道车辆换道紧迫程度的收益[16]，考虑到主线与匝道车辆的不同行驶策略，构建了不同的收益函数，根据纳什均衡的约束条件采用非线性规划方法求解同一博弈对局中双方的纳什均衡策略.通过仿真验证，相比人工驾驶和智能网联环境下无人驾驶无控制合流，所提出的博弈控制模型有效提高了匝道合流区域的通行效率并降低了燃油消耗.

1 博弈模型构建

1.1 入口匝道合流

选取主线单车道与匝道单车道合流的场景，匝道与主线采用加速车道的连接方式，如图1所示.匝道车辆基于行驶目的地需要属于战略性变道，匝道车辆可以在加速车道的任意段选择汇入主线车道，协同控制策略应用于主线与匝道的道路合流区域，路网中行驶的车辆均是具备智能网联功能的自动驾驶车辆，车辆与车辆、车辆与路侧控制单元以及路侧控制单元与道路设施之间均可以实时通信，路侧控制单元可以获取协同控制区域中车辆位置、速度、加速度等行驶状态信息以及道路各车道占有率等交通状态信息.路侧控制单元根据所获取的车辆行驶状态以及道路交通状态信息，基于相应的控制模型计算出合流控制区域内每辆车的行驶策略，并将行驶策略发送给相应车辆[17].

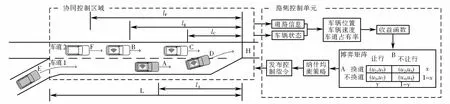
图1 合流区域协同控制系统

当车辆进入协同区域路段后开始实时采集行驶状态信息，通过协同控制系统对区域内车辆发送速度和是否变道的行驶策略指令，协同控制区域道路长度为L，车道1中车辆需要在协同控制区域内完成向车道2的变道，变道指令由路侧控制单元发出.

1.2 换道策略

匝道合流区域中车道1中的车辆A需要在合流区域末端向车道2进行战略性换道，在t时刻车辆A与合流区末端相距为lA，如果A继续在车道1上行驶，随着lA的不断减小，其换道的意愿会愈加强烈；影响A换道时机的是换道目标车道中临近的滞后车辆B和先前车辆C，B和C距离合流区域末端的距离分别为lB和lC，B根据自身当前的行驶状态可以选择减速配合A变道，也可选择加速不配合A变道，在智能网联环境下，车辆之间相互通信，相互可以感知其他车辆的行驶状态和位置，A和B的行驶策略可以认为是基于完全信息下的重复博弈.

完全信息下的重复博弈，博弈主体之间对于局中人、策略集合以及赢得函数都是完全了解的，而且双方在同一时间步内同时决策，没有先后次序，同一对局中的博弈主体都是期望自身在博弈中取得更大的收益[18].定义博弈的参与者集合D∶D={A,B}，A表示的车道1中车辆选择换道和不换道的行驶策略集合S∶SA={SA1,SA2}，车辆A可以选择在目标车道有可插车间隙时选择换道也可以不换道继续在原车道行驶.B表示的车道2中车辆选择让行和不让行的驾驶策略集合S∶SB={SB1,SB2}，对应采取的驾驶行为分别是主动降低车速配合车辆A的换道需求和加速行驶缩小与车辆C的间距使得车辆A达不到换道的最小可插车间隙.由于A和B双方的策略集合不同导致的双方收益也不同，因此该博弈又是一个非对称博弈[19].

1.3 博弈收益分析

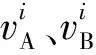
(1)

式中：a和b分别为车辆B选择减速避让和加速不让行的速度变化率；u1为车辆B避让配合A换道时A的收益；u2为车辆B出于自身行驶利益不配合车辆A换道时车辆A的收益.在收益函数中如果只考虑安全因素的影响，就可能达成某个不切合实际的纳什均衡状态，如果A过早的换道至车道2，则有可能增加了车道2的占有率，不仅损失了在车道1行驶更快的通行效率，而且降低了车道2的通行效率；若A迟迟没有完成换道，则随着lA的不断减小，A的换道时机在不断减少，能否顺利完成换道的不确定性也在增大[20]，因此不换道行驶的收益为：

(2)

A选择不换道行驶策略的收益分别为u3和u4，式(2)反应的是车辆A在不换道行驶策略下继续在车道1行驶的换道紧迫程度，动态描述车辆A的换道收益.如图1中博弈矩阵，A选择换道和不换道的概率分别为x和1-x.车辆B的收益函数如公式(3)所示.

(3)

1.4 模型求解

基于完全信息的2×2非对称博弈中，显然车辆A选择纯策略SA1和SA2的期望收益分别为：

(4)

式中：车辆A选择纯策略SA1和SA2的概率分别为x和1-x.则A的平均期望收益为：

E(A)=x[yu1+(1-y)u2]+(1-x)[yu3+(1-y)u4],

(5)

同样，车辆B选择纯策略SB1和SB2的期望收益分别为：

(6)

式中：车辆B选择纯策略SB1和SB2的概率分别为y和1-y.则B的平均期望收益为：

E(B)=y[xu5+(1-x)u7]+(1-y)[xu6+(1-x)u8],

(7)

根据复制动态思想，车辆A和B通过学习会选择收益更高的驾驶策略，纳什均衡状态也会随之改变，由于u=(u1,u2,…,un)(其中n=6)之间的数值关系可能导致非纯策略的纳什均衡，概率值x和y也会发生变化，直至双方达成稳定的纳什均衡状态.x和y的变化速率为

(8)

当一个博弈达到稳定状态时，x和y的数值不再变化，即dx/dt=0，dy/dt=0，这样就得到五个稳定状态(x,y)=(0,0)、(0,1)、(1,0)、(1,1)和(x*,y*)，其中(x*,y*)=((u8-u7)/(u5+u8-u6-u7),(u4-u2)/(u1+u4-u2-u3)),分别对应五种策略集合{SA2,SB2}、{SA2,SB1}、{SA1,SB2}、{SA1,SB1}和A采用x*的概率选择SA1，B采用y*概率选择SB1的混合策略.将上述求解纳什均衡状态转化为非线性规划求解问题，如公式(9)～(11)所示.

(9)

(10)

(11)

其中:0≤x，y≤1且E(A)，E(B)≥0，公式(9)在公式(10)和(11)的约束条件下所得到的x和y的解即为博弈的纳什均衡策略.

2 仿真验证

2.1 仿真参数设定

本文使用SUMO(simulation of urban mobility)仿真软件对博弈控制模型的通行效率进行验证，通过调用其提供的交通控制接口(traffic control interface，TraCI)进行车辆控制[21]，TraCI实时获取车辆状态和道路信息与外部写入的博弈控制模型算法进行联合仿真.采用文献[22]中的匝道合流场景，结合我国高速公路匝道合流区现状，设置协同区域长度L=150 m，主线道路限速100 km/h，匝道道路限速60 km/h.在主线和匝道分别输入25辆小型车，其中车辆进入主线的初始速度范围60～100 km/h，车辆进入匝道的初始速度范围40～60 km/h，车辆加速度限制在-10～2.6 m/s2，仿真步长为1 s.

2.2 仿真实验结果与分析

实验分别选取人工驾驶车辆和智能网联车辆在匝道入口合流区的汇入情况作为对比，其中人工驾驶车辆的跟驰和换道模型采用Wiedemann心理-生理类驾驶行为模型，智能网联车辆的跟驰模型采用协同自适应巡航控制(cooperative adaptive cruise control，CACC).共两组对照实验与博弈控制模型进行对比，仿真结果如图2所示.

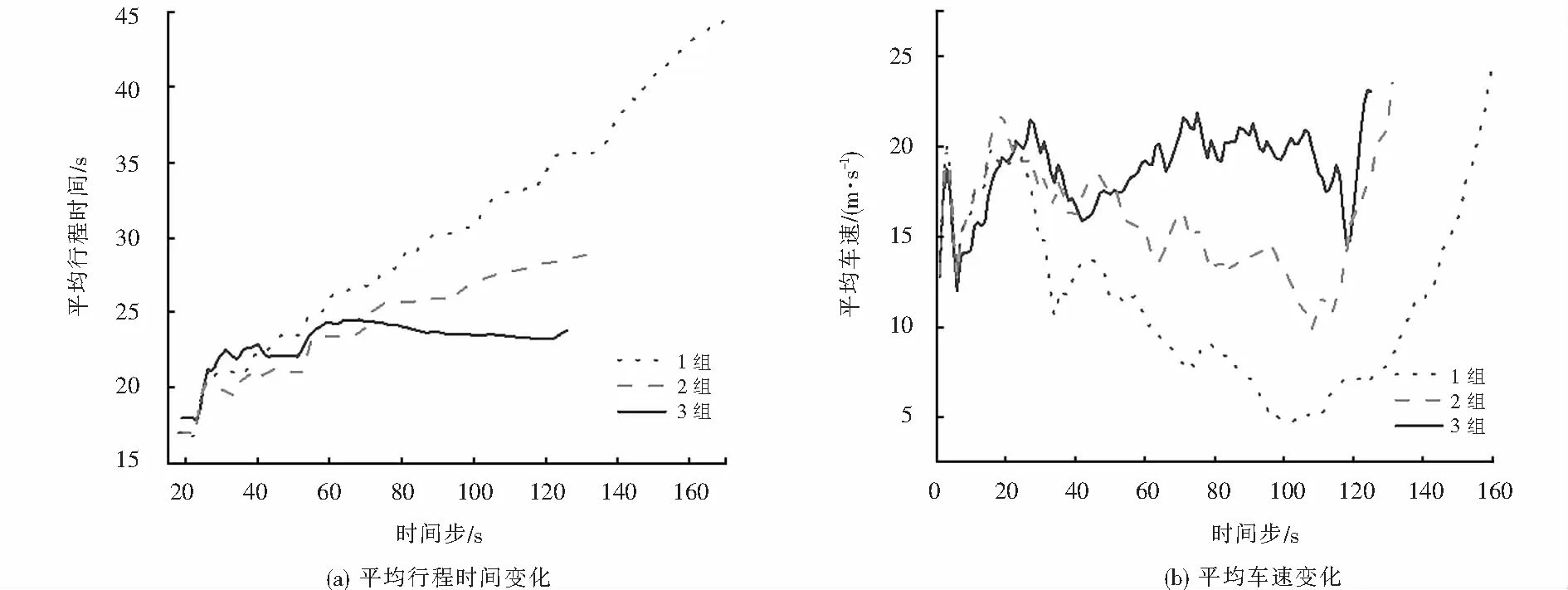
图2 不同控制策略仿真结果

由图2，第3组在每个时间步内当前路网中所有车辆的平均行程时间、平均车速变化波动均最小，图2(a)的第62个时间步，1组中由于路网中车辆达到一定数量，车道1与车道2处于博弈对局中的两辆车在每个时间步中的决策趋于稳定达到了某种纳什均衡状态，随着车辆的继续加载，路网的平均行程时间并没有继续增加，而是整体趋于稳定；而当路网车辆开始减少，路网平均行程时间和平均车速与其他组别相比并没有大幅度变化，说明在智能网联环境下博弈控制策略所形成的纳什均衡状态一定程度上平衡了车流量对路网通行效率的影响，仿真过程的124个时间步3组50辆车的平均行程时间23.80 s、平均车速23.10 m/s，平均车速最小值9.23 m/s与最大值13.87 m/s相差66.55%.2组虽然在车辆通行效率上与3组较为接近，但是车流量增加过程中平均行程时间也在明显增加，车辆在没有协同控制的情况下平均车速受车流量影响变化较大，仿真过程的129个时间步2组50辆车的平均行程时间28.92 s、平均车速23.64 m/s，平均车速最小值9.58 m/s与最大值23.64 m/s相差146.76%.对车道1和车道2中处于博弈对局的两辆车运行状态进行分析如图3所示.

处于博弈对局的两辆车在没有协同控制条件下车辆A由于需要战略性换道，会寻求适当的可插入间隙汇入到车道2，车辆B会依据自身的跟驰规则行驶，如图3，实验车辆间没有协同导致车道1的车辆在没有合适的换道时机时，车道1中处于同一对局的车辆并没有减速让出合适的可插入间隙，导致车道1的通行效率明显高于车道2，降低了道路整体的通行效率；在采用了博弈控制模型的第3组实验中，智能网联环境下处于同一博弈对局中的两辆车在每个时间步的决策时间点上通过计算当前博弈的收益矩阵，基于完全信息做出的决策.第2组共有4辆车在换道时机上没有达成纳什均衡状态，而在第3组的博弈控制模型中这4辆车的换道策略都发生了变化，如表1所列.

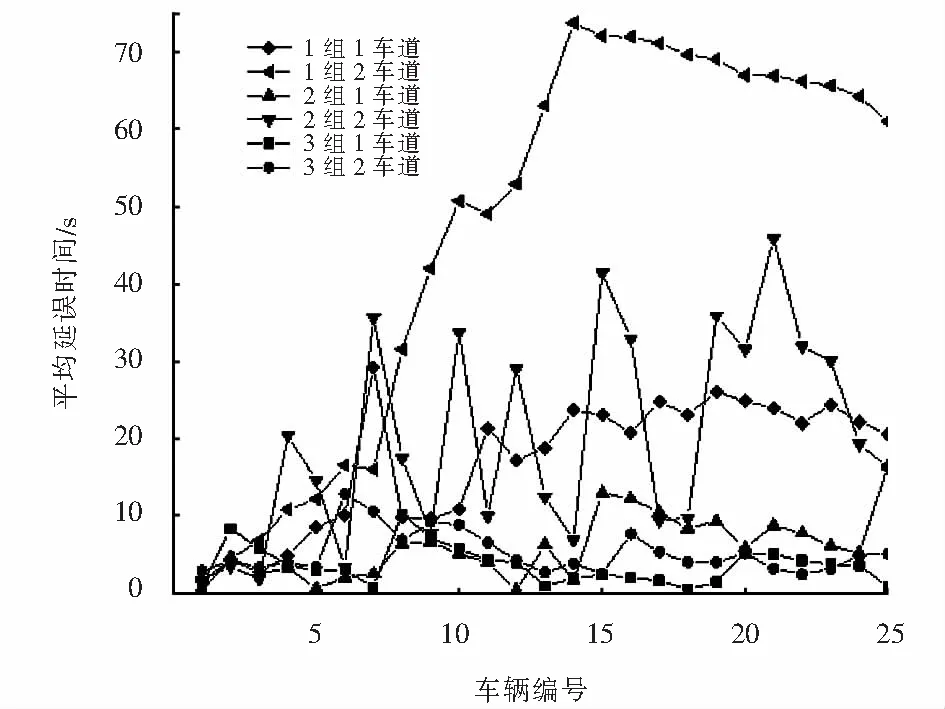
图3 车辆延误情况

表1中p1=u1+u4-u2-u3，p2=u2-u4，p3=u5+u8-u6-u7，p4=u7-u8，第2组的车辆编号11、12、13以及19的车辆在换道时机上并没有选择纳什均衡的最优策略，虽然其它21辆车在各自的博弈对局中都选择的纳什均衡策略，但是由于车辆编号11、12、13以及19的驾驶策略影响，第2组整体的整体通行效率降低.在应用了博弈控制模型的第3组实验中，车辆编号11、12、13以及19的驾驶策略均达成了纳什均衡状态，博弈的仿真结果如图4所示.

表1 纳什均衡状态分析

如图4中(e)、(f)和(d)所示，车辆A与车辆B在博弈对局中达成了纯策略的纳什均衡状态，即(x,y)=(1,1)车辆A选择换道，车辆B选择让行的策略组合，而图4(h)车辆A和B达成了一个混合策略的纳什均衡状态，即(x,y)=(0.69,0.46)，根据纳什均衡状态的定义，当多群体的决策达到某个均衡状态时，该均衡状态下任一博弈方中的任一主体都不愿意单方面改变其现有策略，而博弈方中的任意选择突变策略的主体都无法入侵当前达成稳定状态的群体，此时博弈对局中的双方达成了纳什均衡状态.显然，博弈控制模型的1组实验中改变了车辆编号11、12、13和19的换道策略，使得车道1和车道2中车辆在合流过程达到了更优的通行效率.即是在智能网联环境下，车辆具备了相互位置、速度和加速度情况感知的条件下，仍有调节车辆驾驶行为的必要，如图5(a)所示，车道2中车辆出现了与车道1中车辆协调换道失败的情况.如图5(b)所示，协同控制后的车辆位置变化情况.

图5(a)中仿真开始时由于车流量不大，车道1和车道2车辆可以在不影响通行效率的情况下完成换道；随着车流量逐渐增大，部分车道2车辆错过了某些换道时机，在距合流点较近的区域产生了排队等待换道的情况，进而影响了同车道车辆的换道时机；车道2的拥堵情况不断加剧也影响着车道1中正常行驶的车辆，车道1车辆在仿真的最后也出现了拥堵情况.图5(b)中由于根据博弈控制模型计算出的纳什均衡换道策略，博弈对局中的车辆基本都按照预定驾驶策略行驶，没有产生拥堵，只有车道2中的个别车辆降低了行驶速度，但是并没有对其他车辆造成影响，如图6所示.

图6(a)中车道2车辆在合流过程中出现了速度为零的情况，显然在车流量增大后靠车辆自组织的协调合流已经失效，车道2车辆发生了排队现象，同时车辆的速度出现了大量不规则的波动情况，如图7(a)所示，没有协调控制的合流过程中车辆加速度大幅变化，车辆为获得较高的通行效率采用了急加速和急减速行驶，最大减速度达到了-8.3 m/s2，影响乘车人的乘坐舒适性，对于同车道的后车跟驰行驶也会产生影响，增大了发生追尾事故的可能.如图7(b)所示，车辆加速度变化范围变小.

利用外部程序调用SUMO提供的TraCI接口，获取车辆的实时信息，确定处于同一博弈对局中的两辆车，将车辆的位置和速度信息带入公式(1)、(2)和(3)求解出纳什均衡状态，再通过TraCI将下一时刻的车辆速度和是否换道的驾驶策略发送并控制相应车辆，经协调控制后车辆的速度变化如图6(b)，车辆进入协同控制区域后速度明显改变，部分车辆速度波动很小，接近匀速行驶或是匀加速行驶，个别车辆在某些时刻出现了速度为零的情况，但是并未对其他车辆通行效率造成影响.车辆加速度变化如图7(b)所示，相比协调控制前，加速度的数值更多的集中在-1～2.6 m/s2，在当前车辆出现急减速的情况，相邻后车也立即采用了相同的急减速驾驶策略，并且最大减速度降低到-4.5 m/s2，降低了与后车发生追尾事故的可能.

图6 车辆速度变化

图7 车辆加速度变化

通行效率如表2所列，仿真时长为T，车道1和车道2的平均延误时间分别为t1和t2、平均车速分别为v1和v2、平均车道占有率分别为O1和O2、平均排队长度分别为l1和l2.

表2 车辆通行效率

3组仿真实验中车辆均未发生碰撞，第3组仿真的50辆车用124个时间步最先通过了匝道合流区域，车道1与车道2的平均延误时间相差8.26%、平均车速相差40.09%、平均车道占有率相差261.65%并且均未出现排队现象；与第3组通行效率较接近的是第2组，用时129个时间步完成了实验，其中车道1与车道2的平均延误时间相差66.10%、平均车速相差40.80%、平均车道占有率相差55.08%.可以看出，应用了博弈控制模型后，车道1与车道2中处于博弈对局的两辆车在智能网联环境下感知了对方收益情况，基于完全信息采取的驾驶行为策略达成了纳什均衡状态，使得车道1与车道2的通行效率趋于均衡.

由于车辆加速、减速以及频繁启停对车辆运行油耗也会产生影响，实验分别选取人类驾驶人驾驶车辆(1组)和智能网联环境无人驾驶(2组)以及智能网联环境博弈控制模型(3组)的合流过程进行对比，不同条件下车道1和车道2的累计油耗如表3所列.