声学多普勒测流中的谱矩估计及应用

杨永寿 王忠康

（杭州瑞利海洋装备有限公司，杭州，310023）

多普勒声呐是一种测量自然和人工水道中水流速度及剖面流量的声学设备，由于具备不干扰水流场、测量精度高和测量成本低等优势，已经广泛应用于水文测量、海洋研究、水资源勘探和水下导航等诸多领域[1-3]。

宽带声学多普勒测流信号是一随机过程，通常具有有限的平均功率，可以用功率谱密度（Power Spectral Density，PSD）相关方法来描述、分析和处理。基于功率谱矩估计的测流信号处理方法因具有精度高、应用广等优势而逐渐获得研究人员的重视。文献[4]基于准平稳和高斯随机信号模型，利用单延迟自相关和全谱估计等谱矩估计方法研究了大气探测雷达中的参数估计和干扰抑制问题。文献[5]利用协方差法推导了伪噪声序列一阶谱矩和二阶谱矩的均值和方差表达式，指出一阶谱矩的均值是多普勒频移的无偏估计，方差与子序列的相关系数、信噪比和时宽带宽积有关。文献[6]提出了一种基于谱密度函数理论的谱矩函数分析方法，旨在同时计算电荷密度和谱函数，并提出了一种利用前 4个谱矩计算谱函数的有效算法。文献[7]针对具有加性复高斯噪声的随机信号，基于谱矩估计原理推导了其频率和谱峰宽度的均值和方差的渐进估计表达式，其方差估计的主导项与Cramer-Rao下界相同。文献[8]提出了一种利用自相关函数计算高阶谱矩的算法，用于分析非高斯功率谱天气雷达观测信号。与离散傅里叶变换（Discrete Fourier Transform，DFT）和脉冲对方法相比，该算法具有计算量小、准确度高等优势。文献[9]提出了一种利用随机信号的协方差样本估计任意阶谱矩的算法，并利用该算法计算了极地无线电信号经电离层衰减所得接收信号的谱矩，验证了算法的有效性。文献[10]利用四阶谱矩估计和深度学习研究了利用脑电波信号进行情感检测的方法，谱矩估计用于检测脑电信号的非线性和非高斯性。

现有的底速估计方法（如匹配滤波法）通过优选能量最强或者与发射波形相关性最大的底回波分段得到底速。然而，能量最强、相关性最大回波分段的速度估计误差却不一定是最小的。受旁瓣干扰的影响，底回波前段的信噪比有所下降。在底速估计时，如能避开受污染的回波段则可提高底速估计的精度。本文所述宽带回波是指宽带编码发射信号的散射回波经数字解调后所得信号。

本文从谱矩估计的原理出发，推导了宽带回波的归一化一阶及二阶谱矩表达式，据此设计了一种基于互相关系数的底速估计方法和一种基于信噪比的测流数据统计方法，两种方法可显著减小底速和流速的估计误差。

1 旁瓣对底回波的干扰

在多普勒测流中，主波束通常倾斜向下，波束轴线与垂向成 20°～30°夹角。现有换能器存在与主波束成 30°～40°夹角的旁瓣。在主波束没有达到底部之前，旁瓣已经到达底部。在一定深度条件下，较强的旁瓣底回波会淹没主波束回波的接收，从而污染底回波信号。这种污染可能导致3种影响：（1）受污染底回波分段的能量增大；（2）局部底回波的信噪比下降；（3）底回波功率谱的谱峰展宽，因为旁瓣底回波与主瓣底回波中包含了不同的多普勒信息。

旁瓣干扰底回波的示意图如图1所示，图中水底以下部分仅为示意，并非实际声波传播路径。由图1中的红色弧线可知，旁瓣底回波先于主瓣底回波到达换能器，由图1中的黑色弧线可知，旁瓣底回波污染了主瓣底回波的前段，进而导致现有匹配滤波方法底速估计误差的增大。

图1 旁瓣对底回波的干扰示意图

2 谱矩估计及其拓展应用

2.1 谱矩估计

假设宽带声学多普勒测流信号具有时间平稳性和空间均匀性，对于任意非负可积多普勒测流回波的PSDS(ω)，定义其k阶矩为

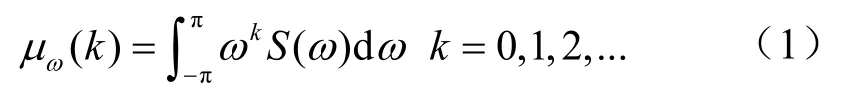
宽带测流中的多普勒频移均值可由其 PSD的归一化一阶矩来估计[7]：

由于 PSD的计算复杂度较高且其噪声抑制能力没有自相关方法强，所以使用自相关方法进行参数估计更加实用。根据 Wiener-Khinchin定理，自相关函数R(τ)与PSD的关系如下：

式中，τ为自相关延迟。分别求式（4）的一阶和二阶导数，并令结果中的τ=0，得到PSD零阶矩、一阶矩和二阶矩与自相关函数的关系式：

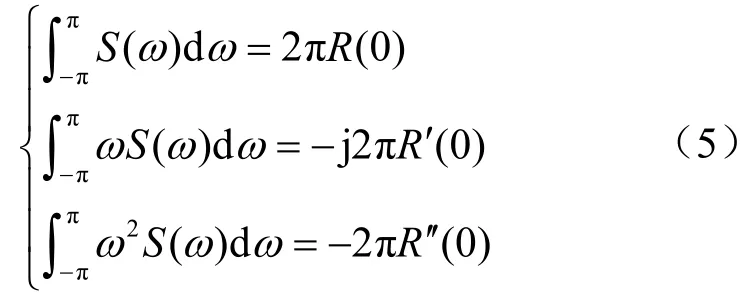
综合式（2）、（3）和式（5），得到

接着推导自相关函数一阶和二阶导数的计算式。宽带回波的复自相关函数可表示为极坐标形式：

式中，A(τ)为幅度函数，φ(τ)为相位函数。对式（8）两边分别求一阶和二阶导数，并利用A(τ)是τ的实偶函数，φ(τ)是τ的实奇函数的特性可得

综合式（6）、（7）和式（9），可得

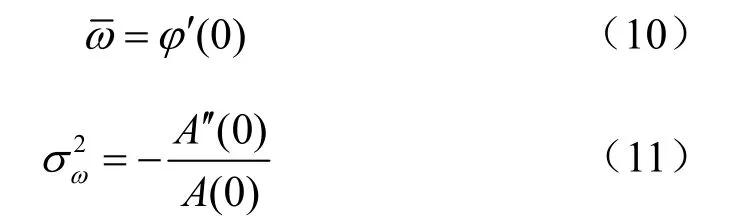
对φ(τ)在τ=0处进行泰勒展开并取前两项，得到φ'(0)≈[φ(τ)-φ(0)]/τ，且φ(0)=0；对A(τ)在τ=0 处进行泰勒展开并取前三项，得到A"(0)≈2[A(τ)-A(0)]/τ2；由式（8）可知A(τ)=|R(τ)|，A(0)=R(0)。综合可得利用自相关函数计算PSD谱矩的表达式为

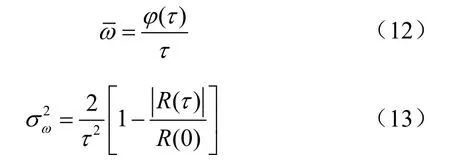
式（12）～（13）分别为多普勒频移均值和方差的估计表达式。式（13）中，|R(τ)|表示时延为τ的两段回波互相关的模值，R(0)等于回波中噪声与信号的总功率，|R(τ)|/R(0)表征以上两段回波的相关性。由式（13）可知，|R(τ)|/R(0)的值与频率估计方差成反比。

根据以上原理，设计了一种基于互相关系数的底速估计方法和一种基于信噪比的测流数据统计方法，可减小底速和流速的估计误差。

2.2 基于互相关系数的底速估计方法

由第1节的分析可知，受旁瓣污染的影响，主瓣底回波前段的信噪比下降、功率谱峰展宽，其与后段未被污染底回波的相关性将显著下降。|R(τ)|/R(0)可以用来表征两段回波的相关性，本文在式（13）的基础上设计了如式（14）所示的底回波优选判据ηb，用于优选受旁瓣干扰最小的底回波分段。

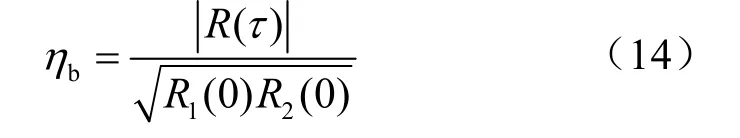
式中，R1(0)和R2(0)分别为参与复自相关运算的两段回波信号样本的自相关。底回波信号的ηb判据值越大，其前后两段的相关性越强，表示受旁瓣污染的程度越轻。利用ηb判据可以优选受旁瓣干扰最小的底回波段，进而提高底跟踪速度估计的精度。

2.3 基于信噪比的测流数据统计方法

由于实际测流回波的信号功率一般较小，式（13）中等号右侧的表达式对于回波信噪比的敏感度不高，不适合作为数据统计分析的判断依据。本文在式（13）的基础上设计了一种测流数据统计分析判据ηv。

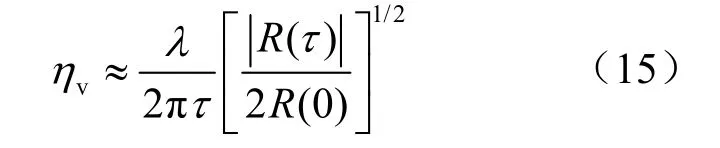
式中，|R(τ)|/R(0)表征分层回波前后两段信号的相关性，其值越大即ηv越大则分层回波的信噪比越高，流速估计的误差也就越小。测流仪器实时计算水体分层回波的ηv，对ηv数值小于设定阈值的测流数据予以剔除，或替换为合格数据的均值。

3 试验验证与分析

利用外场试验结果验证基于互相关系数的底速估计方法和基于信噪比的测流数据统计方法的性能。外场试验河段长约1 km，河面宽度约60 m，测船静止试验处的水深约为 3.3 m，测船运动试验河段的平均深度约为 5.5 m。所用试验仪器为一台600 kHz宽带声学多普勒测流试验系统。

3.1 底速估计方法对比试验

试验样机波束1在测船静止条件下的单次回波样本如图2（a）所示，此时底速的理论值为零。逐点滑动计算与发射脉冲等长的回波段的判据值ηb与底速估计误差，并与匹配滤波法进行了对比，结果如图2（b）所示。图2（b）中红色粗实线表示ηb判据，灰色实线表示匹配滤波判据，ηb判据的值基本与底速估计误差呈反比，这与理论预测一致。红色和灰色虚线分别表示本文底速估计方法和匹配滤波法根据各自判据最大值确定的底回波起点3.995 ms和3.92 ms，其对应的底速估计误差分别为-0.076 m/s和-0.222 m/s。本文方法的底速估计误差相对减小了66%。

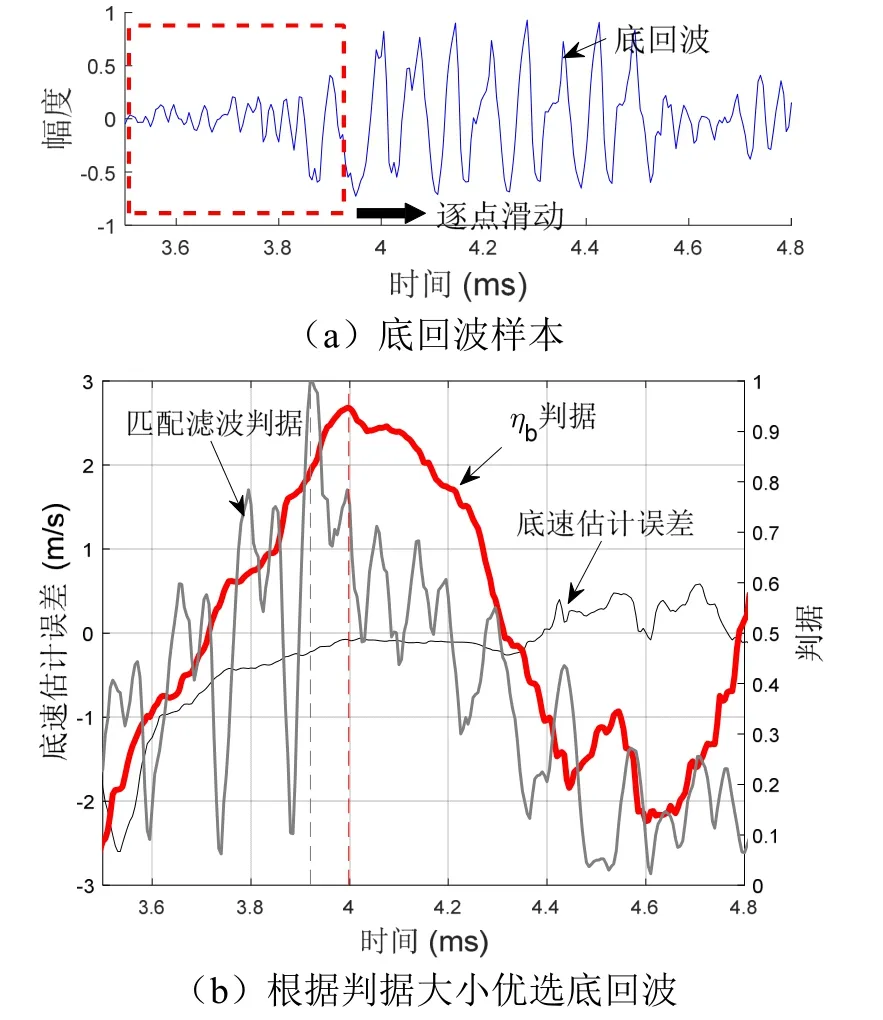
图2 单个样本的底回波优选方法

分别利用本文方法和匹配滤波方法对测船静止试验中的100个样本进行底回波优选，结果如图3所示。

图3 多个样本的底回波优选结果分析

图3（a）中红色方形和黑色圆圈分别表示本文方法和匹配滤波法优选的底回波时间起点，红色和黑色实线分别表示对应的最小二乘拟合结果。本文方法所选底回波起点总体上比匹配滤波方法延迟约0.065 ms。将图3（a）中匹配滤波法所得底回波起始时刻减去互相关系数法所得底回波起始时刻，结果如图 3（b）中黑色三角所示。图 3（b）中大部分的差值为负，说明本文方法确定的底回波起点大部分处于相对靠后的位置。由第1节的分析可知，底回波的前段受到接收旁瓣的影响，虽然其与发射信号的相关性最大，但信噪比明显下降，最终导致底速估计的精度不如底回波的后段。图3（a）中底回波起点随样本延后的趋势是因为试验时测船随风浪摇晃。

分别使用本文底速估计方法、匹配滤波法估计测船静止和运动条件下单波束、100个样本点的底速，结果如图4所示。静止条件下的试验结果对比如图4（a）所示，两种方法估计的速度均值都接近零，但匹配滤波方法的波动幅度明显较大。运动条件下的试验结果对比如图4（b）所示。

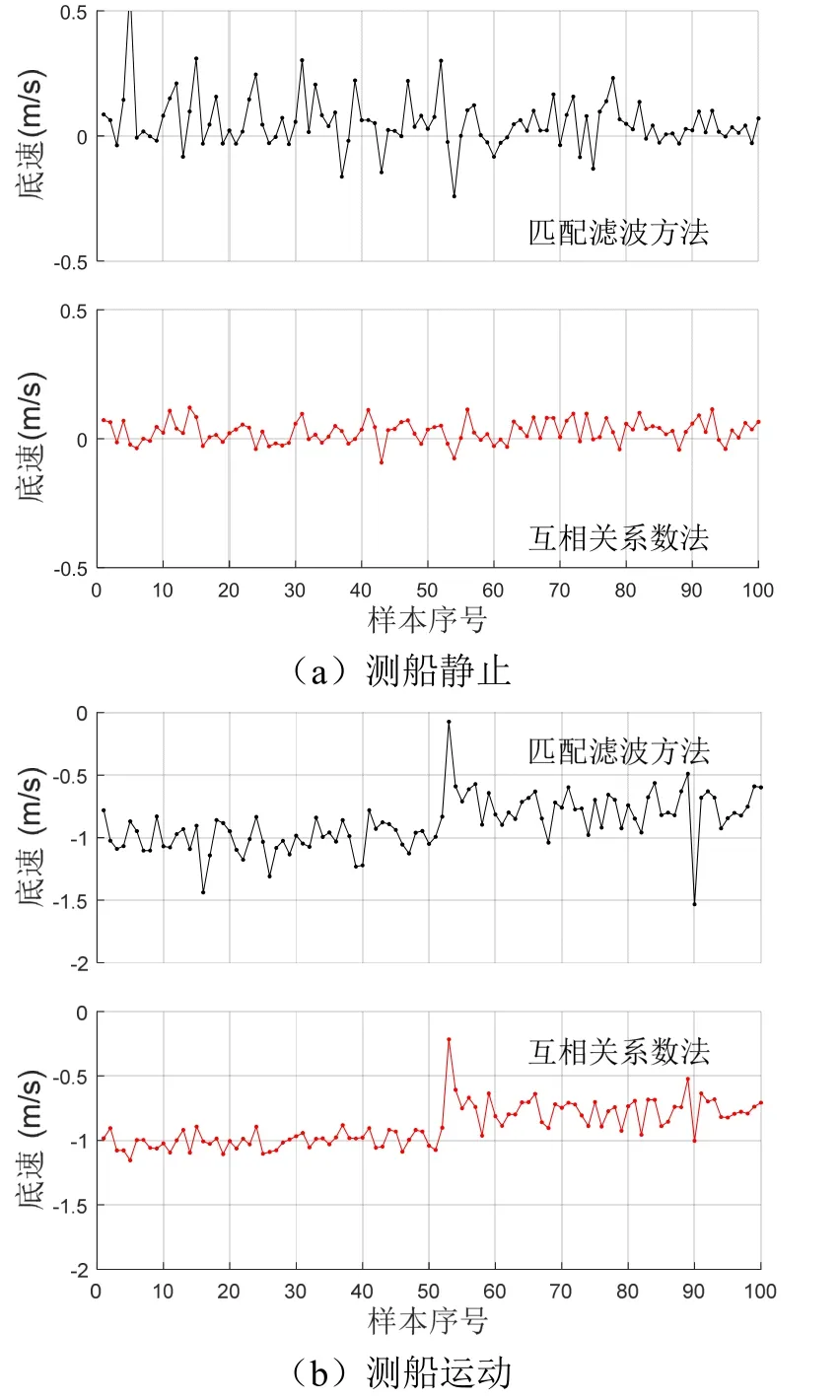
图4 两种底速估计方法实测底速对比

图4中两种方法估计的速度均值约等于理论值，但本文方法的波动幅度明显较小。测船运动条件下，底速曲线前后部分的速度均值变化明显，是因为在第50个样本点附近测船转向，船速发生了改变。

两种方法的底速估计标准差对比见表 1。相比匹配滤波法，测船静止和运动条件下本文方法的速度标准差分别减小了60%和50%。

表1 两种方法底速估计标准差对比 单位：m/s

3.2 测流数据统计分析试验

利用第2.3节所示方法对测流试验系统波束3的第2层径向流速估计结果进行统计分析，总样本数为100，径向流速的理论值是1 m/s。计算得到的统计分析判据曲线如图5（a）所示。判据大小介于0～1之间，根据经验确定判据小于 0.3的样本不合格。不合格样本用统计分析后合格样本的均值替换。统计分析前后的径向流速标准差对比如图5（b）所示。图5（b）中灰色点划线表示统计分析前的径向流速，其标准差为 0.779 m/s；图 5（b）中红色实线表示统计分析后的径向流速，其标准差为 0.352 m/s。经本文方法统计分析后，径向流速标准差减小了约55%。

图5 测流数据的统计分析

为了直观展示统计分析判据与速度估计标准差之间的关系，将图 5（a）中判据ηv按大小进行排序，并按排序后的样本顺序对图5（b）中统计分析前的数据进行重排，再计算重排后每个样本点前向15个样本的速度估计标准差，第1～14个样本的前向标准差均用第15个样本的结果代替，处理结果如图6所示。结果表明判据越大，回波的信噪比越高，对应的流速估计误差越小，与理论预测一致。

图6 流速标准差与统计分析判据的关系

4 结论

为提高宽带多普勒测流方法的估计性能，本文基于随机信号功率谱矩估计原理推导并设计了一种基于互相关系数的底速估计方法和一种基于信噪比的测流数据统计方法。两种方法均可利用自相关运算实现，具有计算复杂度低、实时性好、估计精度高等优点。本文获得的结论如下：

（1）由于宽带测流中采用倾斜波束布局，底回波前段受到接收旁瓣的影响而信噪比明显下降，底速估计时避开受旁瓣污染的回波段可显著降低底速估计的误差。

（2）|R(τ)|/R(0)表示延迟为τ的两段回波分段的相关性，宽带多普勒测流中，|R(τ)|/R(0)的值越大说明回波信噪比越高，流速估计的误差也就越小。

（3）本文设计的基于互相关系数的底速估计方法可显著提高底跟踪速度的估计精度。实测数据分析结果表明，在测船静止和测船运动两种条件下，底跟踪速度标准差分别减小了60%和50%。

（4）本文设计的基于信噪比的测流数据统计方法可明显提高水流速度的估计精度。实测数据分析结果表明，在径向流速理论值为1 m/s条件下，数据筛选后径向流速标准差减小了约55%。