和田玉超声波数值模拟分析及回波信号特征分析∗

王家乐，章翔峰，司呈鑫，马铜伟，李 军

(新疆大学 机械工程学院，新疆 乌鲁木齐 830017)

0 引言

和田玉作为新疆特有的玉石，其主要成分为钙镁硅酸盐，还包含透闪石、角闪石、阳起石等成分[1]，是透闪石和阳起石系列矿物中的一种.由于和田玉的形成环境比较复杂，所处环境也比较恶劣，所以和田玉在形成过程中受到撞击或外力挤压时难免出现一些缺陷.裂纹缺陷在和田玉中属于最为常见的一种缺陷，同时也影响着和田玉的观赏性和艺术价值.和田玉中的裂纹缺陷分为由外部向内部延伸的可见裂纹和在内部无法观测到的潜在裂纹[2]，外部裂纹可通过肉眼观察到，而潜在裂纹如果在加工前不能被及时发现，会对玉石的加工品质造成严重的影响，影响玉石的观赏性，严重时会造成珍贵玉石材料的浪费，甚至损害消费者的利益.因此，需要对和田玉内部缺陷进行无损检测研究.

随着现代各类无损检测技术的快速发展和应用，超声波检测方法因为其独特的穿透能力强、指向性好、对材料无损害和成本低等特点，在无损检测中占据着重要的地位[3]，被广泛应用于岩石无损检测领域.目前大多数的超声无损检测的测量介质都是金属材料，岩石材料作为一种天然材料，与金属材料相比较而言其结构疏松，回波信号衰减大，噪声多[4]，而目前针对和田玉内部缺陷的信号分析研究成果较少.

根据超声波的反射现象，声波在介质传播的过程中，若介质材料内部的结构发生变化或者介质内部含有其它介质，且声波在两者之间的传播声速有较大差异，则声波的一部分会绕过另一种介质继续向前传播，另一部分会发生反射.由于传播路径发生变化，导致回波信号波形发生变化，因此可以根据波形的变化来判断试件内部是否有缺陷以及分析出缺陷的位置和大小等.

本文根据和田玉样本实际检测过程的需要，建立了和田玉超声波无损检测有限元仿真模型，通过静电场、声场和固体力学场之间的相互耦合，计算求解得到和田玉裂纹的回波信号，将信号数据保存后进行特征分析.最后通过超声波检测设备对和田玉试件进行检测，并对实际采集的信号进行特征分析，验证和田玉仿真模型的有效性.

1 仿真模型的原理及建立

1.1 仿真模型的原理

超声检测方式采用压电超声无损检测，其检测结构图如图1所示，图中红色部分是在有限元仿真软件中所仿真的部分.其原理为波形发生器发出一束脉冲信号，脉冲信号通过信号放大电路传递给压电超声探头，探头中的压电材料在受到电信号后发生形变，而后产生高频震动进而引发出超声信号，声波在试件中传播，待接收到返回的回波信号时，压电超声探头再将声信号转换为电信号，最后将采集到的信号进行保存.

1.2 仿真模型的建立

1.2.1 和田玉的声速计算

为计算和理论分析考虑，通常将玉石材料看成是各向同性的弹性材料[5].根据各向同性介质的线弹性本构方程[6]构建和田玉弹性力学模型：

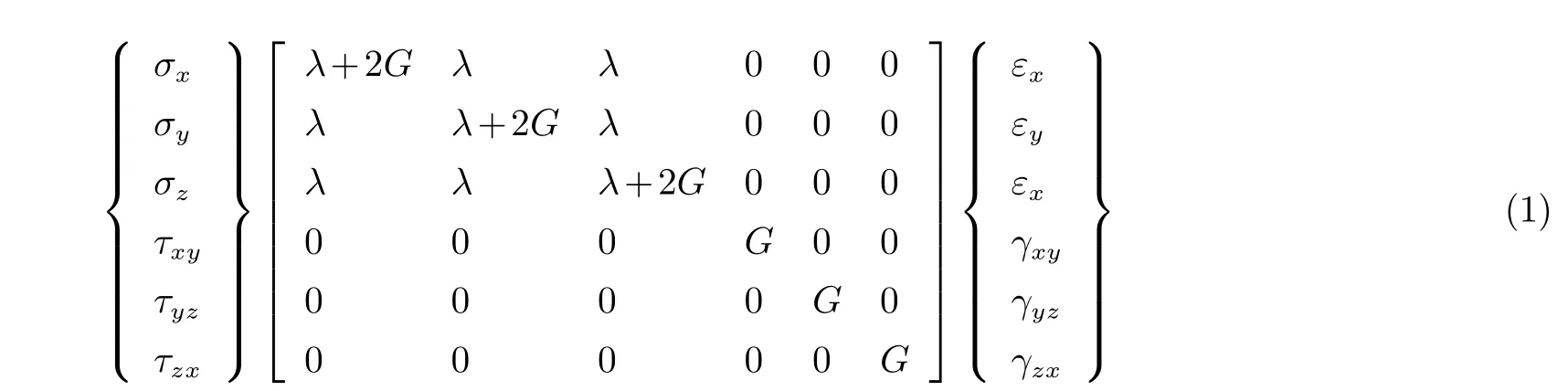
将式（1）简写为：

式中：εx、εy、εz分别为x,y,z方向的应力，γxy、γyz、γzx分别为xy,yz,zx平面的应变，e=εx+εy+εz为体应变，G为剪切模量.

声波在均匀各向同性的线弹性连续介质的传播遵循下列弹性方程.

本构方程：

式中：Dijkl为刚度系数，其中的非零元素为D11、D12、D44，且有关系式：D44=(D11-D12)/2.

平衡方程：

式中：fi为体力；ρ为介质的密度.

几何方程：

由式（3）～（5）得各向同性介质的弹性动力学方程：

令fi=0，可得纵波声速为：

本文中假设玉石试件无限大，和田玉的密度经测量为2.95 g/cm3.经计算，该和田玉声速近似为Cp=3 500 m/s.声速（c）、超声波频率（f）和波长（λ）3个物理量之间的关系可表示为：

1.2.2 建立有限元模型

利用COMSOL Multiphysics建立有限元仿真模型，分析缺陷位置变化与超声波信号特征之间的关系，结合和田玉的材料属性[7]，按图2建立仿真模型.

图2 仿真流程图

首先构建仿真过程中所用材料的几何模型，其中包括超声波探头、被检测试件（和田玉）和试件中所含有的缺陷（裂纹）；在建立完几何模型后，分别为几何模型添加材料属性，各组件材料如表1所示.探头在仿真软件中定义为固体力学物理场和静电场的耦合场，被检测试件以及缺陷均定义为压力声学场，在探头与被检测试件中间添加探针，用来接收超声信号；本次建模假定被测试件无限大，为了消除被测试件内侧两壁产生的回波信号，将被检测试件的左右两个边界均定义为平面波辐射边界[8]，从而消除两壁回波对缺陷的回波进行干扰；同时将探头上边界添加为支撑辊，防止在仿真过程中产生额外的超声信号；采用四边形网格对几何模型进行划分，被检测试件的最大网格尺寸值为λL/Δxmax>8[9]，其中：λL为超声波纵波波长，Δxmax为最大网格尺寸；为保证计算时间和计算精度达到最优值，取最大网格尺寸为0.014 mm.采样频率f=1/2.5 MHz，经计算求解后的总时间为18 μs.

表1 材料属性

图3为建立的和田玉几何模型.仿真模型的尺寸为20 mm×50 mm，裂纹的尺寸为0.25 mm×6 mm，改变探头与缺陷之间的距离，计算出仿真模拟信号.

图3 和田玉仿真几何模型图

物理场为声-固耦合物理场，在探头与被测试件接触面处施加制定位移载荷，载荷采用2.5周期正弦函数与经过连续二阶导数平滑处理的方波函数进行调制，中心频率为2.5 MHz，其波形如图4所示.

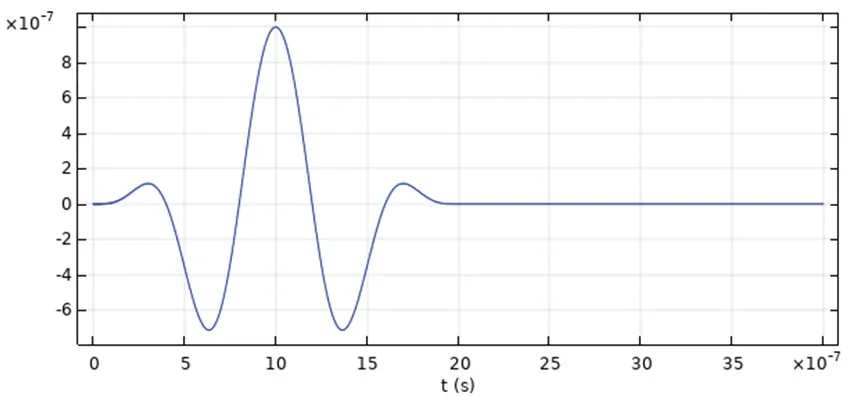
图4 激励信号波形图

2 建立仿真信号的分析

2.1 缺陷位置对超声波信号的影响

根据所建立的仿真模型，缺陷位于探头正下方7 mm处，图5为仿真模型分别在2.6 μs、5 μs、6.6μs时刻下的波场快照.

图5 不同时刻波场快照

从图5（a）可以看出，超声探头经过高频振动产生具有一定能量的脉冲超声波信号，超声波在尚未到达裂隙缺陷前以正常方式传播，声波分为两个部分，其中一部分为传播速度较慢的横波，另一部分为传播速度较快的纵波，纵波与横波相互作用，产生了能量较强的瑞雷面波[10].由图5（b）可知，超声波的纵波成分先于横波到达缺陷位置，声波在到达缺陷位置时发生部分反射，反射波按原传播路径向上传播，并到达上表面边界.图5（c）显示了声波的绕射现象，即声波绕过裂隙继续向下传播并将在某处交汇，在到达下边界后发生全反射，形成底面回波.从声波在波场传播的特征上可以看出，声波的传播过程完全符合弹性波在固体中传播的理论.由于左右边界釆用平面波辐射边界，计算区域内未受到左右两边界反射波的影响，这也表明本文采用的平面波辐射边界是有效的.

为探究不同位置下缺陷对信号的影响，将缺陷置于探头的正下方，缺陷与探头之间的距离依次设置为3 mm、7 mm、11 mm、15 mm，其时域波形图如图6所示.

由图6可知，回波（a）为缺陷位于探头正下方3 mm处的回波信号，由于距离最近，回波（a）的缺陷回波个数最多，随着缺陷与探头之间的距离变大，从回波（a）、（b）、（c）、（d）中能明显的看出回波个数有所减少，其中回波（a）含有a1～a7七个缺陷回波，回波（b）具有b1、b2两个缺陷回波，回波（c）和回波（d）仅有c1和d1一个缺陷回波.由于声波在介质传递过程中不断衰减，回波（a）中的缺陷回波a1～a7的幅值逐渐降低，在回波（b）中幅值b1＞b2，由于回波（d）中的缺陷位置距离探头最远，其缺陷回波的时间也就越长，幅值也相对降低.

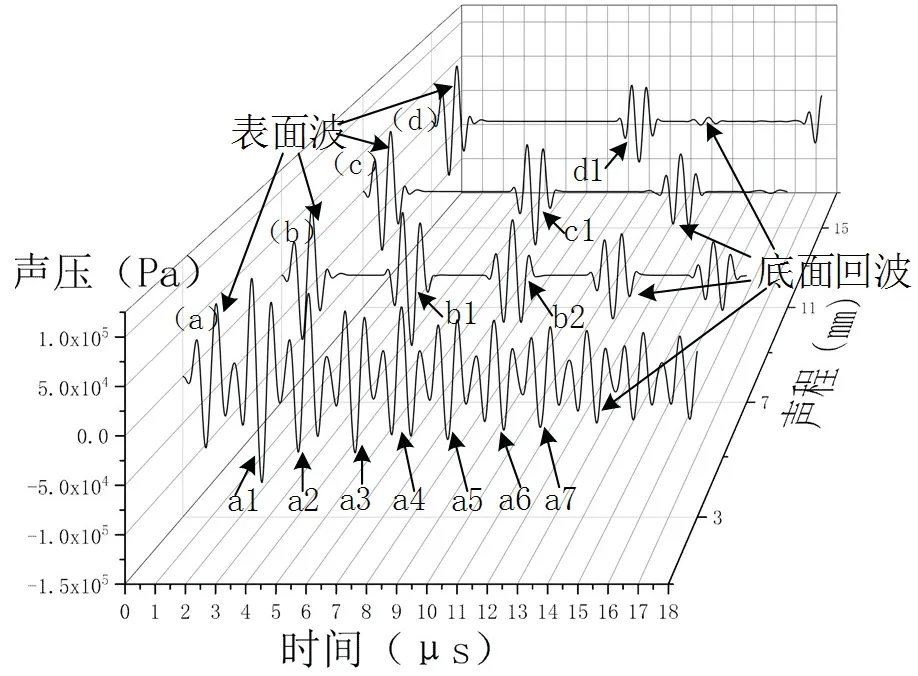
图6 不同缺陷位置波形图

为分析时域信号的特征，挑选计算时域信号的峰峰值（xvpp）、整流平均值（¯x）、方差（xν）、均方根（xrms）、波形因子（S）、峰值因子（C）、峭度因子（kr）、脉冲因子（I），共计8个特征[11]如表2所示.其中峰峰值、整流平均值、均方根从不同角度反映出接收信号的能量大小；方差反映信号与其均值之间的偏离大小程度；峰值因子、脉冲因子反映信号的陡峭或扁平程度；波形因子反映波形轮廓；峭度因子反映信号脉冲特性反应的程度.

表2 时域特征

经过计算，不同声程下的特征值具体如表3所示.可以看出随着声程增加，峰值因子、脉冲因子、峭度因子、波形因子增大；峰峰值、整流平均值、方差、均方根减小.

表3 时域特征结果

2.2 频域特征分析

对获取到的仿真信号进行频域分析，图7中的（a）、（b）、（c）、（d）分别为声程3 mm、7 mm、11 mm、15 mm的回波信号频域图.从图7可以看出频率主要存在三个主峰，分别分布在0～0.5 Hz，0.5～1.5 Hz，1.5～2.5 Hz范围内，其中0～0.5 Hz的峰值最高，其余的两个波峰峰值逐次降低.随着缺陷回波的声程减小，回波信号的主频能量逐渐增大且主频成分也逐渐突出，低频部分也相对增大.随着缺陷声程的减小，信号的主频能量的峰型上的尖锐峰也随之增多，这是由于声程减小，缺陷的回波个数增多，声波在介质传播的过程中的频率不发生变化，只是能量值不断衰减，因此在时频转换过程，同一频率的幅值也就越大.

图7 不同缺陷位置频域图

同样选取方差（xν）、均方根（xrms）、峰值因子（C）、峭度因子（kr），共计4个特征对频域信号进行分析，可以看出随着声程增加，峰值因子增大；方差、均方根、峭度因子减小，如表4所示.

表4 频域特征结果

2.3 信号EMD分解能量熵分析

和田玉内部缺陷会造成缺陷周围材料组织发生变化，导致材料的声阻抗发生变化，从而使超声信号所包含的信息成分发生变化.将信号中所包含的信息能量化，通过能量的变化分析出缺陷与超声信号之间的变化关系[12].首先通过EMD方法对信号进行逐层平稳化分解处理，产生一系列具有不同尺度特征的IMF分量数据序列.再对所得的IMF分量进行能量计算[13]：

（1）计算前m个IMF的能量：

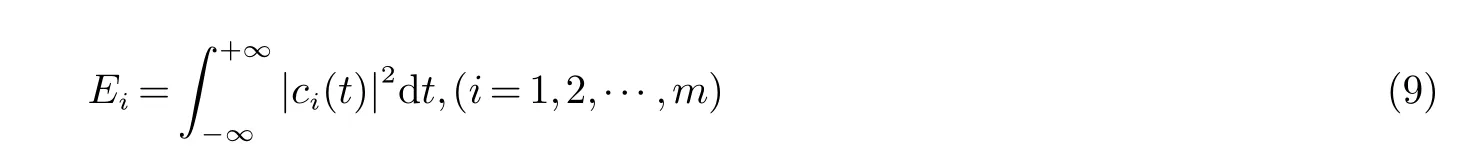
（2）每个本征模态分量的能量分布系数为：

（3）由于能量值较大，为了便于分析和处理对E进行归一化.设：

不同声程的回波信号经EMD分解后，其IMF分量所具有的能量分布如图8所示.从图8可以看出其能量主要分布在第一个IMF分量中，随着声程增大，能量值也随之减小.不难看出经EMD分解后各缺陷在不同频段的能量分布上有着显著的差异且具有一定的规律性.

图8 能量分布图

3 回波信号分析试验

3.1 缺陷试块及检测信号采集

此次试验采用的超声波设备为武汉中科HS620数字式超声波探伤仪，根据试验所获取的材料参数，选择中心频率为2.5 MHz的双晶直探头对和田玉样本进行超声波信号检测，并对其信号进行处理.本文采用30 mm×40 mm×15 mm（长×宽×高）的和田玉作为试验对象，在试件侧面人工切割出一道裂纹，裂纹位于检测面约6 mm处，采用压电脉冲反射法对含缺陷试件进行超声检测，对同一试验试件正反两面进行超声检测信号提取，从而获取不同声程的超声信号.和田玉试件及其裂纹如图9所示.

图9 和田玉试件

3.2 检测信号分析

探头放置在含缺陷试件上，移动探头到缺陷处后，发现始波和底波之间出现缺陷波.稳定探头，调节增益至70%，按下定量按钮，记录波形.调整探头的位置，对含缺陷的试件进行多次超声波信号采集，得到对应的回波波形见图10，其中图10（a）、图10（b）分别为声程6 mm、9 mm的时域图.

如图10中的两个缺陷回波所示，在缺陷处，始波与底波之间出现多个缺陷波，回波幅值逐渐降低.和田玉中的缺陷为裂纹，裂纹内一般处于真空状态，声压透过率小，反射回声也大部分被内壁散射[14].裂纹等同于锯齿状反射体，入射声波会向各个方向反射，导致反射回波的散射严重，从而导致超声波探头所能接收到的信号减弱.当裂纹的面积大于探头的面积时，由于声压透过率小，回波信号较弱，再加上声波在玉石中传递的衰减扩散，回波信号往往不能够清楚的采集到.

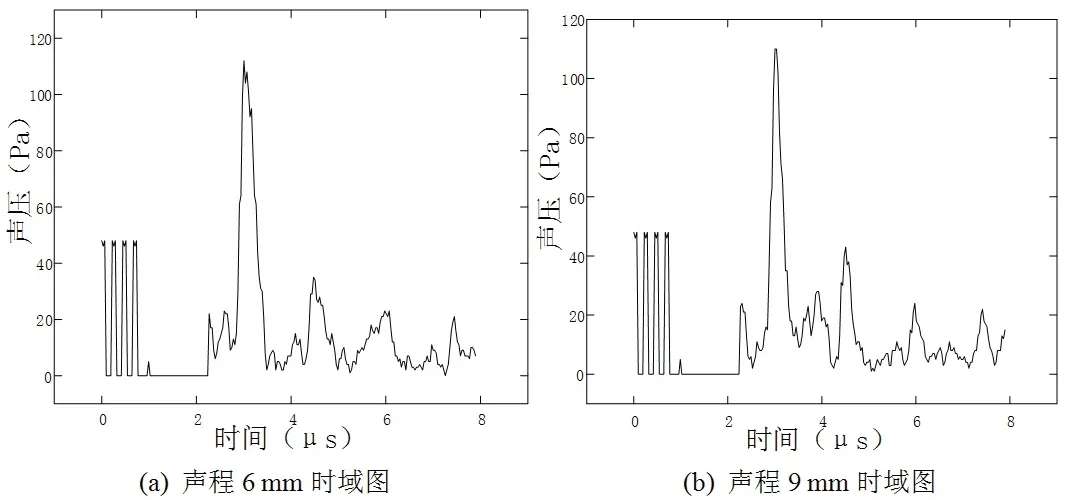
图10 试验信号采集

再将采集到的声波信号进行时频域变换，得到的频域图如图11所示.从图11可以看出，6 mm声程的主峰幅值略大于9 mm声程的主峰幅值，且两者同样含有三个波峰，这与仿真结果一致.

图11 试验信号频域图

同样选择峰峰值、整流平均值、方差、均方根、波形因子、峰值因子、峭度因子、脉冲因子8个特征作为时域特征.随着声程的位置增大，峰值因子、脉冲因子、波形因子、峭度因子增大；峰峰值、整流平均值、方差、均方根减小.选择方差、均方根、峰值因子和峭度因子4个特征作为频域特征，从计算结果可以看出，随着声程增大，峰值因子增大；方差、峭度因子、均方根减小.具体结果如表5所示，其结果与仿真结果基本一致.

表5 试验信号特征结果

将试验采集的回波信号经EMD分解后，其能量分布如图12所示，从图12可以看出，随着声程增大，各IMF能量值也随之减小.

图12 试验信号能量分布

4 结论

（1）本文针对和田玉无损检测，建立了基于压电超声无损检测的有限元仿真模型，并对仿真信号进行分析，该模型灵活方便，操控性强.

（2）经过信号分析发现该仿真模型信号的时域、频域和IMF分量能量中均包含多种特征，特征分析全面、具体，这些特征对缺陷的进一步诊断有很大参考作用，该模型可用于指导超声信号在和田玉中的传播特性检测研究.

（3）通过试验信号与仿真信号对比发现，仿真信号所存在的特征变化规律与试验信号的特征变化规律基本一致，验证了仿真模型的有效性和正确性.