基于价格弹性和行为选择的共享停车动态定价方法研究
2022-02-12汪义路叶晓飞闫星辰
汪义路,叶晓飞,2,李 敏,陈 峻,闫星辰
(1.宁波大学 海运学院,浙江 宁波 315211;2.宁波市港口贸易合作与发展协同创新中心,浙江 宁波 315211;3.东南大学 交通学院,江苏 南京 210096;4.南京林业大学 汽车与交通工程学院,江苏 南京 210037)
0 引言
随着小汽车保有量的高速增长,城市停车供需矛盾日益突出,其中,停车供需矛盾最突出的是土地开发强度高、人口密集、交通需求庞大的城市中心区。停车难问题严重制约了城市中心区可持续发展,其中存在的主要问题是停车收费经济杠杆作用不显著。共享停车能够有效地整合城市停车设施资源,使相邻的土地使用者共用停车设施,从而降低整体停车泊位需求总量[1],并结合动态定价发挥停车收费经济杠杆作用,有利缓解停车难问题。然而,现有停车价格经济杠杆作用不显著,表现在:(1)城市中心区与其他区域收费价格之间差距不显著,片区内部各用地类型停车设施收费价格倒挂现象严重,尤其是路内、路外停车收费价格倒挂严重。(2)在选择停车场的过程中缺乏价格提示信息,大多数停车者遵循“有车位就停放、先停放后付费”的行为惯性。(3)现行停车价格体系仅1 a, 3 a或更长才调整1次,未考虑停车价格与供需的互动关系。这都说明现行价格体系难以成为管理者缓解停车难问题的有效手段,难以引导停车者选择行为,难以发挥调节供需的作用。
停车定价研究可分成静态定价和动态定价。静态定价主要采用经济学原理和定价理论,对停车设施进行成本定价[2]、需求差异定价[3-5]、区段定价[6]及最优定价策略[7],并逐渐建立了停车行为选择、停车意愿、停车价格、出行特征等因素之间的相互关系模型[8-9]。动态定价在停车领域理论和实践应用方面均引起了广泛关注,西雅图P-Bpark项目[10]对核心商业区内的10个街区及周边200个街区的路内停车设施实行以停车占有率为依据的动态定价政策,每年根据实际停车占有率调查数据调整4次费率。尝试类似政策还有旧金山SFpark项目[11]和洛杉矶ExpressPark项目[12]等。学者们[13]依托这些项目充分论证了停车动态定价实践可行性和有效性,认为停车占有率被成功控制在目标水平,动态定价能够引导停车需求的再分布。Ghent[14]认为SFpark项目定价算法过于粗糙,应采用路段级占有率数据而不是总占有率作为定价依据,建议进一步缩小停车占有率目标区间(60%~80%)和调整周期(每月),使得价格变化更为敏感。陈峻等[15]构建了停车选择行为与停车价格的关系模型,提出了动态平衡的共享停车浮动收费方法。梅振宇等[16]构建了基于Agent停车仿真模型,评估了不同停车定价策略的有效性,但仍缺乏针对多种类型组合停车场动态供需关系的动态定价研究。因此,本研究通过MNL模型分析短时共享停车情景下停车者对多种用地类型停车设施的行为选择,构建共享停车需求价格弹性模型,并提出基于行为选择和价格弹性的共享停车动态定价方法和流程,充分发挥价格在调节共享停车供需关系的作用,缓解停车供需矛盾。
1 考虑多用地类型停车选择行为MNL模型
1.1 多项Logit模型
非集计模型的理论基础是随机效用理论,该理论是假设停车者在进行相应的决策时追求“效用”最大化这一假说。那么,停车者i选择方案j所带来的效用函数为[17]:
Uij=xijβ+εij(i=1,…,n;j=1,…,J),
(1)
式中,xij为第i个停车者对于第j个选择方案的解释变量;εij为随机项;β为解释变量xij的系数。
停车者i在进行停车选择时选择方案j,当且仅当方案j的效用高于一切其他方案,故停车者i选择方案j进行停车的概率可写为:
P=(Y=j|xij)=P(Uij≥Uik,∀k≠j)
=P(Uik-Uij≤0,∀k≠j)
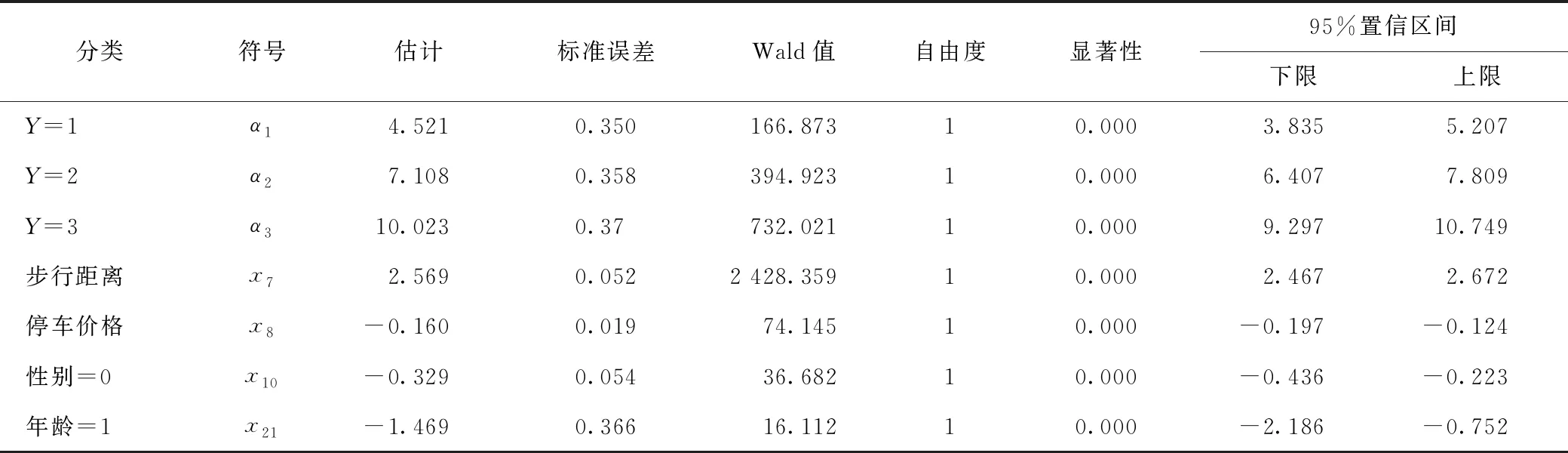
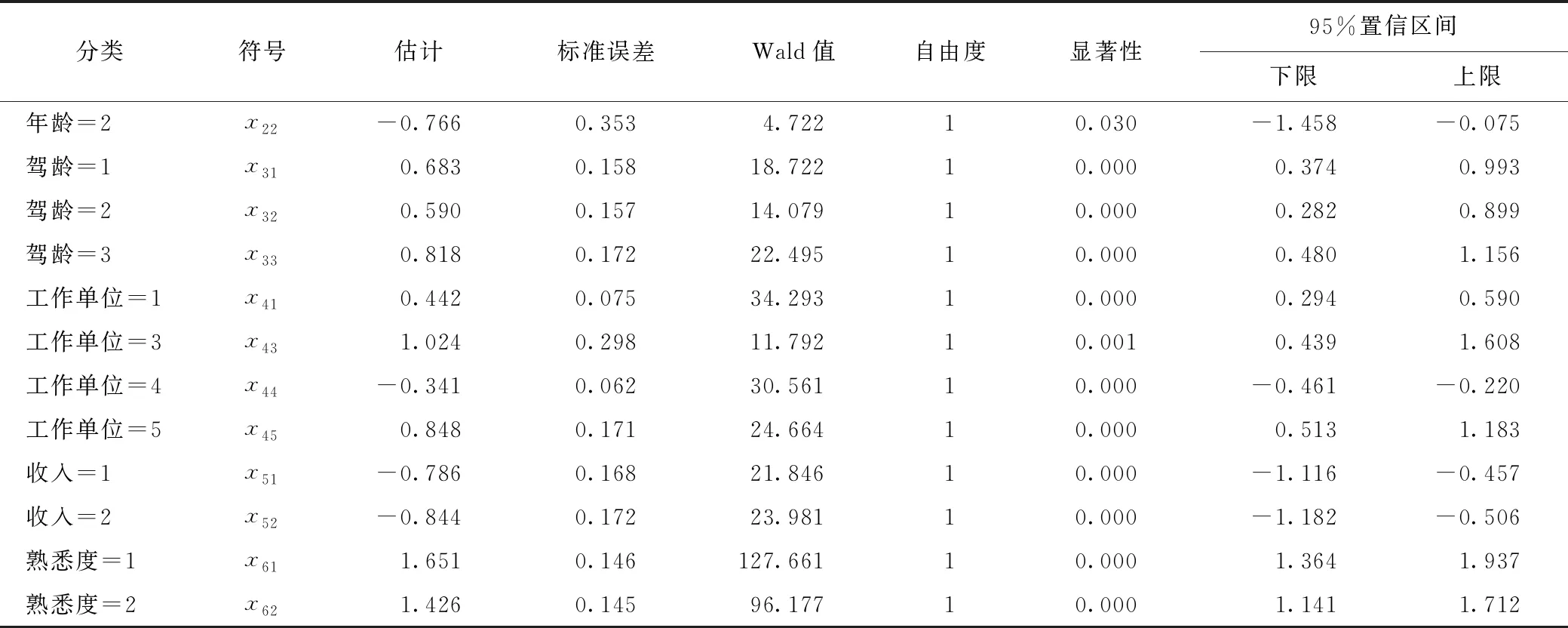
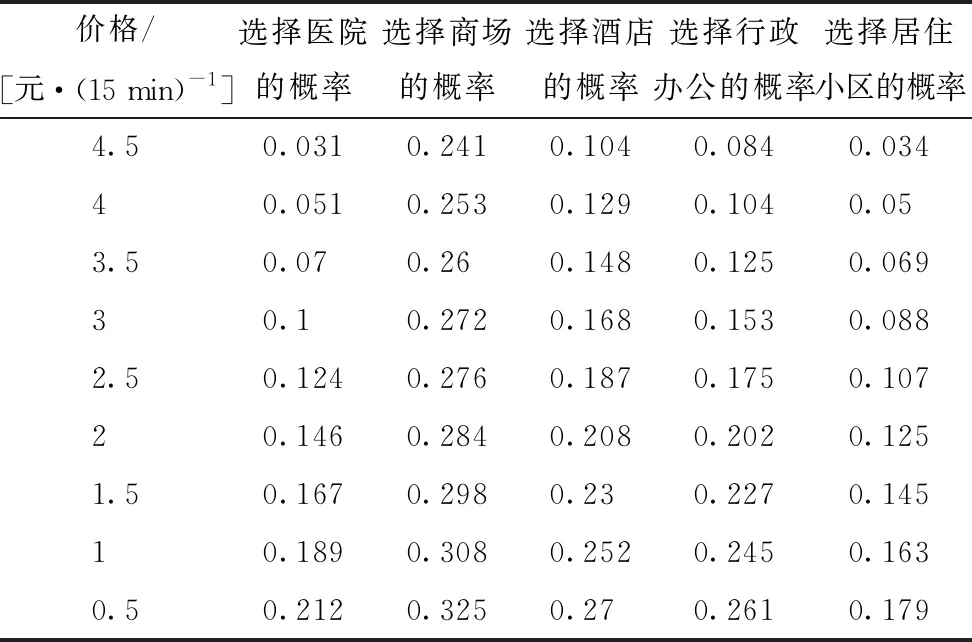
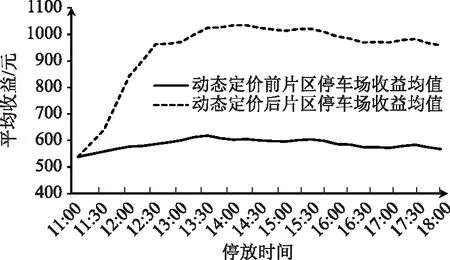
=P(εik-εij (2) 式中,P(Y=j|xij)为停车者i选择方案j的概率;Y为选择方案的合集;Uij和Uik分别为停车者i选择方案j和方案k的效用函数;xik为第i个停车者对于第k个选择方案的解释变量;εik为随机项。 当ε服从二重指数分布时,经迭代可得MNL模型: (3) 式中,j=1,2,…,J-1;X为自变量的集合;αj为第j个选择方案的截距;xk为第k个自变量;βjk为第j个选择方案第k个自变量的回归系数;P(Y=j|X)为第j个选择方案的概率。 选择第J个方案的概率为: (4) 多项Logit模型在短时停车情景下的因变量有不改变自己的停车选择、医院、商场、酒店、行政办公、居民小区,将因变量转换为Y=0为不改变自己的选择,Y=1为医院,Y=2为商场,Y=3为酒店,Y=4为行政办公,Y=5为居民小区。选取性别、年龄、驾龄、工作单位、月收入、熟悉度、步行距离、停车价格8个影响因素为自变量。用于多项Logit模型的特征变量,如表1所示。 表1 自变量定义 以宁波城隍庙、天一广场为研究区域,以停车者为研究对象,采用线下和线上问卷调查2种方法进行数据收集。最终,共回收问卷426份,其中线上问卷242份,线下问卷184份,无效问卷18份,有效问卷共408份。利用调查数据,得到自变量和常数项的估计值。若显著性水平小于0.05,说明该影响因素对停车者的行为选择有显著影响。从参数估计结果可知,性别、年龄、驾龄、工作单位、月收入、熟悉度、步行距离、停车价格8个因素对停车者的行为选择有着显著性影响。通过以上分析,将影响不显著的因素去掉,得到停车者行为选择预测模型。根据有序多分类Logit回归分析,得到表2中的标定结果,只陈列显著性值小于0.05的变量,在95%的置信水平下,各自变量对因变量都有显著影响。 表2 短时共享停车行为选择模型标定 续表2 需求价格弹性指价格变动的比率所引起的需求量变动的比率,即需求量变动对价格变动的反映程度[18]。需求价格弹性有3种模型: (1)线性模型 D=a+bP+rY, (5) 式中,D为停车需求量;P为停车价格;a,b,r分别为待定系数;Y为影响因素变量,可以是毛收入、步行距离等某一重要因素。 (2)半对数模型 D=a+blnP+r1Y1+…+riYi+…+rnYn, (6) 式中,Yi为各影响因素变量;ri为各影响因素变量对应的系数。 该模型表明停车需求量D是停车价格P的对数和变量Y的对数的线性函数。 (3)对数模型 lnD=a+blnP+r1Y1+…+riYi+…+rnYn。 (7) 该模型表明停车需求量D的对数是停车价格P的对数和变量Y的对数的线性函数。 通过设计停车场利用率与停车价格调查问卷,调查停车场A的饱和度分别为90%,85%,80%,75%,70%,65%,60%的情景下,存在另一个距目的地距离相近的停车场B,并且停车场B与停车场A相比相对空闲,当停车场A的停车费用发生变化时,停车者的选择也会变化如何。图1为综合饱和度下的需求价格函数。整合各个饱和度下的数据进行计算分析,得出以下模型。 图1 综合饱和度下的需求价格函数 线性模型为: D=-20.786P+493.03,R2为0.865 3,MAE为0.231 6。 调整的主要目的是对于管线的碰撞关系,特别是对于整体性的碰撞分析的办法,需要对各项洞口的朝向进行整体调整。若存在洞口的朝向问题,可能会导致会发生墙体或柱体的碰撞现象。因此,需要在实际操作中加入合理的预留孔进行校准,保证其保温管道的预留合理性[3]。同时,需要在实际调整中进行项目出图,利用实际的数据参数和基本信息进行4D全息的技术分析,对重要的部位进行标识和核查,确保机电各专业的使用情况与软件所切合,最终达到专业的技术管理的价值。 半对数模型为: D=-330.9lnP+1 072.5,R2为0.893 2,MAE为0.131 5。 对数模型为: lnD=-2.034lnP+10.61,R2为0.902 8,MAE为0.123 8。 R2的数值大小反映趋势线的估计值与对应的实际数据之间的拟合程度。R2趋于1时,可靠性最高。MAE的数值大小反映了预测值与真实值之间的吻合程度,MAE趋于0时,模型误差越小。通过对比,对数模型的可靠性最高,所以选择对数模型lnD=-2.034lnP+10.61为综合饱和度下的停车需求价格弹性模型。 在共享停车状态下,确定在以停车占有率为基础进行动态定价调整之后,需要考虑调整的几个关键参数,即调整的时间间隔、单次调整幅度及价格调整的上下限。在前面章节中求得的停车用地类型多项Logit模型和停车需求价格弹性模型的基础上,分别将参数设置为15 min[19]、价格幅度λ=20%×初始价格、初始价格的20%~180%,具体情况如表3所示。 表3 短时共享停车情景下停车价格动态调整幅度及方法 确定了关键参数后,对短时共享停车情景下以停车占有率为基础,动态调节收费价格的流程如图2所示。 图2 动态定价调节停车需求流程图 (1)确定短时停车情景下,停车设施Sn开放共享的时间窗口T, 开放共享后,以15 min为间隔,将短时停车情景下的共享时间窗口T划分为不同的时间段,记为ti,i=1,2,3,…,n,例如t1为开放共享之后的第1个15 min,t2为开放共享后的第15~30 min,以此类推。 (2)统计停车设施Sn的总泊位数OSn及各停车设施开放共享前一时间段t0的泊位占有数、占有率、收费价格OSn0,RSn0,FSn0。各共享停车设施开放共享时的初始价格相等即FS,0=FS,0-FS,0-FS,0-FS,0。将各停车设施的占有率状态分成4个区间,即[0, 60%),[60%, 85%),[85%, 100%),[100%,∞),分别标记为j=1,2,3,4。 (3)对于第ti时间段,新到达共享停车设施Sn的车辆数为MSni,离开停车设施Sn的车辆数为NSni,那么该时间段的净驶入Sn的车辆数为MSni-NSni。如果净驶入车辆数MSni-NSni>0,则继续步骤4;否则,第ti时段共享停车设施Sn不存在需要对外共享的停车需求。 (4)通过表4可得到不同收费价格下停车者对于停车设施的选择概率。记PSn(FSni)为ti时段收费价格为FSni时,潜在的停车者中选择共享停车设施Sn进行停车的概率。 表4 不同价格下的选择概率 (5)根据上时段ti=1共享停车设施Sn的停车占有率RS,i=1,求各共享停车设施的驶入需求VSni。 如果RSni-1≥100%,那么ti时段由于共享停车设施Sn饱和而前往其他未饱和停车设施的车辆数为VSni1=(MSni-NSni)×PSn(FSni-1),其中VSni1为由于停车设施Sn饱和而产生的前往占有率较低的停车设施Sn的驶入需求(优先选择占有率低于85%的停车设施),PSn(FSni-1)为在价格为FSni-1时溢出的停车需求中选择停车设施Sn进行短时停车的概率。 如果85%≤RSni-1<100%,可以分为2种情况进行讨论: ①ti时段净驶入车辆数MSni-NSni加上前一时段泊位占用数QSni-1后依然小于等于停车设施总泊位数时,即OSni-1+(MSni-NSni)-OSn=OSni-OSn≤0时,在ti时段,愿意前往占有率较低的共享停车设施的车辆数为VSni2=(MSni-NSni)×PSn(FSni-1),VSni2为Sn不饱和情况下而产生前往占有率未达到85%的停车设施Sn的共享停车驶入需求,在这种情况下vSni1=0。 ②ti时段净驶入车辆数Msni-Nsni加上前一时段泊位占用数OSni-1后大于停车设施总泊位数时,即OSni-OSn>0时,那么Sn存在2部分驶入需求,一部分是Sn未饱和的时候,因为其他共享停车设施价格较低或停车占有率低从而放弃该停车设施而选择其他占有率较低(优先选择占有率低于85%)的Sn的需求VSni2=(OSn-OSni-1)×PSn(FSni-1),另一部分为净驶入车辆中因为停车设施饱和而前往其他占有率较低的Sn的共享停车驶入需求VSni1=(OSni-OSn)×PSn(FSni-1)。 如果RSni-1<85%,也可分为2种情况进行讨论: ①ti时段净驶入车辆数MSni-NSni加上前一时段泊位占用数OSni-1后依然小于等于停车设施目标泊位数时,即OSni-1+(MSni-NSni)-0.85OSn=OSni-0.85OSn≤0时,那么在ti时段不存在对外共享的停车需求。 ②ti时段净驶入车辆数MSni-NSni加上前一时段泊位占用数OSni-1后大于停车设施目标泊位数时,即OSni-0.85OSn>0时,那么此时存在因为价格低或停车占有率低从而放弃该停车设施而选择其他占有率未达到85%的Sn的需求VSni3=(OSni-0.85OSn)×PSn×(FSni-1)。 综上,共享停车设施Sn的驶入需求VSni为VSni=VSni1+VSni2+VSni3。 (6)计算ti时段共享停车设施Sn开放共享后的停车占有率RSni和停车占有率状态JSni。 根据ti时段共享停车设施Sn自身的需求及产生的停车驶入需求VSni,从而求得ti时段共享停车设施Sn的停车占有率RSni=(OSni+VSni)/OS,其中OSni为停车设施Sn在ti时段自身需求所产生的泊位占用量。将该时段停车设施的停车占有率记为JSni。 (7)根据ti时段共享停车设施Sn的停车占有率jSni调整短时共享停车情景下的停车场收费价格FSni。 ①当JSni=1时,即停车占有率低于60%,此时根据表3,将收费价格降低幅度λ从而吸引更多的共享停车需求,即FSni=FSni-1-λ。 ②当JSni=2时,即停车占有率在60%~85%范围内,此时根据表3,不需变动收费价格,即FSni=FSni-1。 ③当JSni=3时,即停车占有率高于85%,此时根据表3,将收费价格提高幅度λ从而抑制更多的共享停车需求驶入,即FSni=FSni-1+λ。 (8)重复步骤③,继续整个动态定价流程的循环,直到关闭停车共享窗口的时刻,完成短时共享停车情景下该时间窗口内共享停车收费价格的浮动收费过程。 短时共享停车情景下,周末出行时,目的地附近有5个对外开放共享的停车设施,分别为医院、商场、酒店、行政办公和居住小区。综合整理各个停车设施的数据,得出每个时段片区内开放共享的组合用地停车场动态定价前后的选择概率均值、占有率均值和停车收益均值,如图3~图5所示。在行为选择概率方面,与动态定价前相比,动态定价后片区组合用地停车场选择概率均值是下降的,可知动态定价方法在抑制共享停车需求方面是有效可行的。停车占有率方面,通过动态定价方法定价后,片区组合用地停车场占有率均值得到了提高,动态定价方法大大提高了片区组合用地停车设施泊位利用率。在停车收益方面,与动态定价前相比,动态定价后片区组合用地停车场收益均值得到了提高,动态定价方法大大提高了片区组合用地停车场收益。综上,动态定价方法对于调节停车需求、提高组合用地停车场占有率和停车场收益是有效、可行的。 图3 动态定价前后片区停车场选择概率均值 图4 动态定价前后片区停车场占有率均值 图5 动态定价前后片区停车场收益均值 通过问卷调查获取停车者对用地类型停车设施行为选择的影响因素数据和不同停车场占有率下停车者的选择数据,建立了MNL模型和停车需求价格弹性模型,并提出了短时共享停车情景下基于行为选择和价格弹性的停车场动态定价条件需求的方法与流程。通过算例分析得出,该方法很好地提高了片区内开放共享的各种用地类型停车设施的空闲泊位利用率,缓解了高饱和度停车设施的泊位紧张情况,更好地挖掘了多种共享的用地类型的泊位资源潜力,可应用于中心城区域多种用地类型停车场共享停车动态定价。结果表明:(1)在短时停车情景下,停车者在进行停车选择时主要考虑步行距离和收费价格2个影响因素,在价格增加8元时,大多数停车者会改变自己的停车选择;(2)60%~85%为理想泊位占有状态,当共享停车场占有率低于60%时,降低价格幅度从而吸引更多的停车需求;(3)当停车场占有率高于85%时,上涨价格幅度抑制更多停车需求的涌入,这样附近停车设施的停车占有率才能保持在较为理想的水平。1.2 特征变量选择
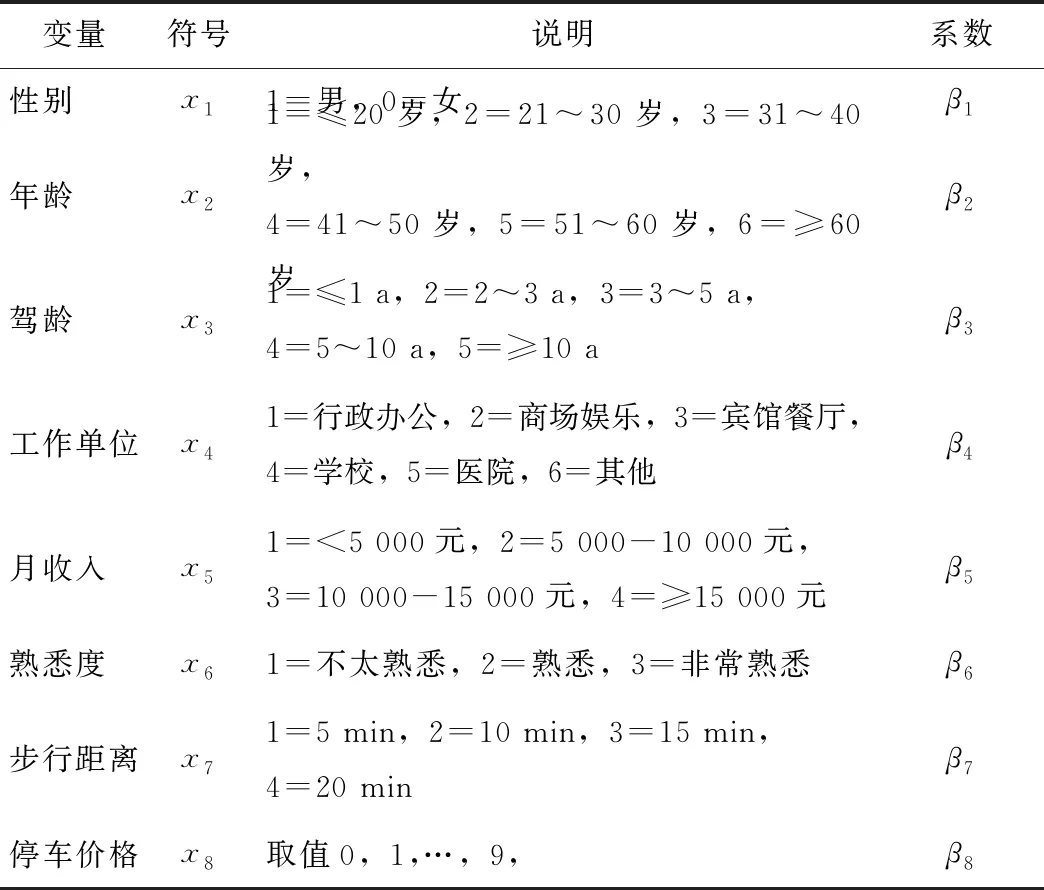
1.3 参数估计
2 共享停车需求价格弹性模型
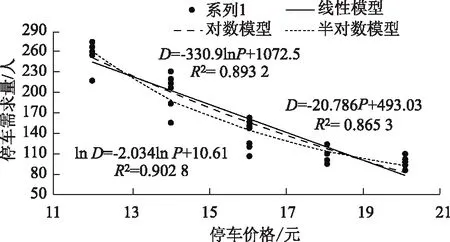
3 多用地类型停车设施动态定价方法
3.1 动态定价流程分析

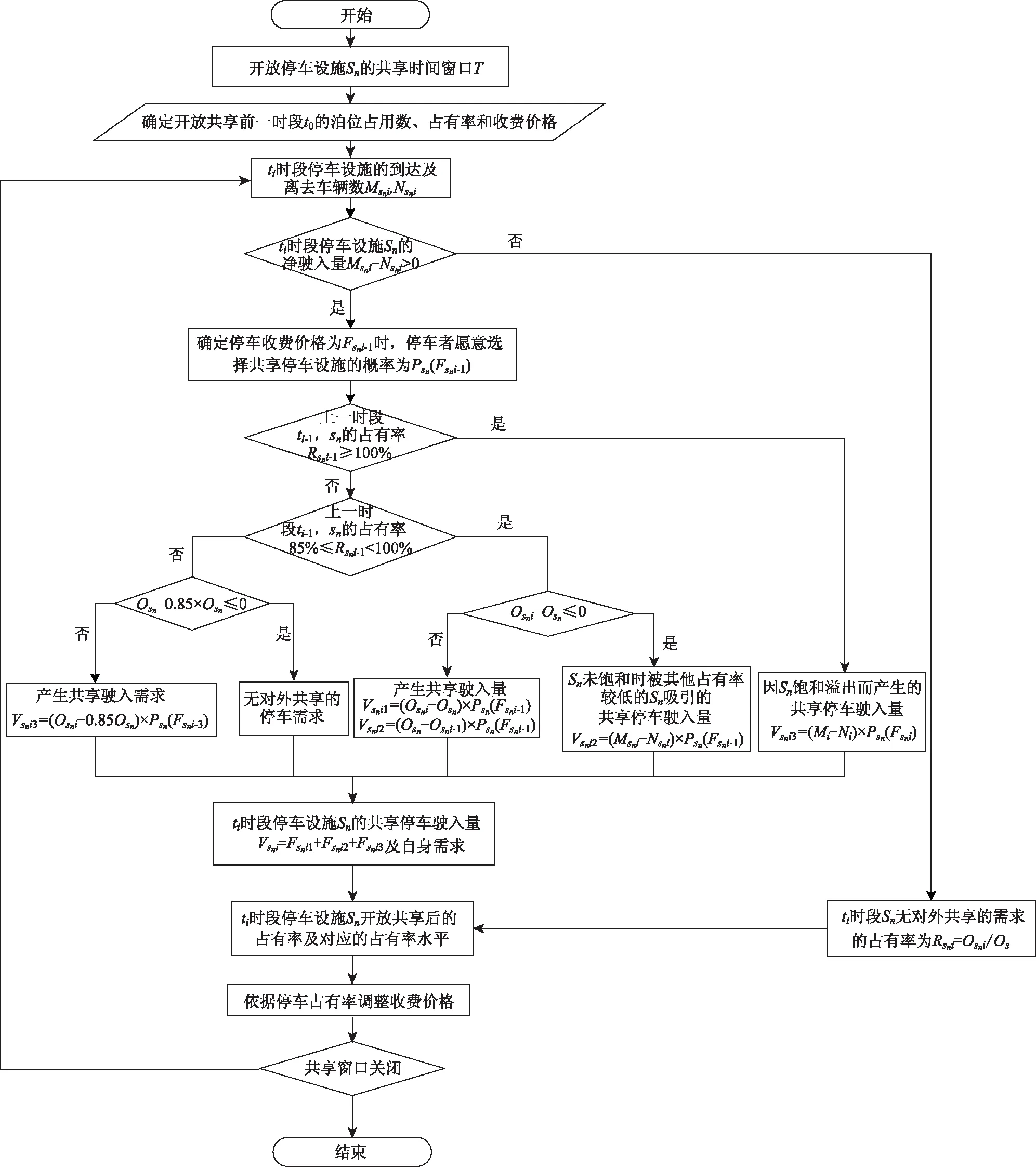
3.2 动态定价效果分析
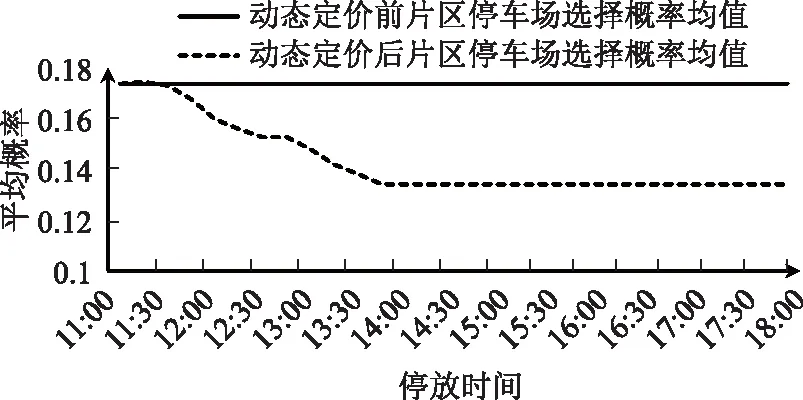
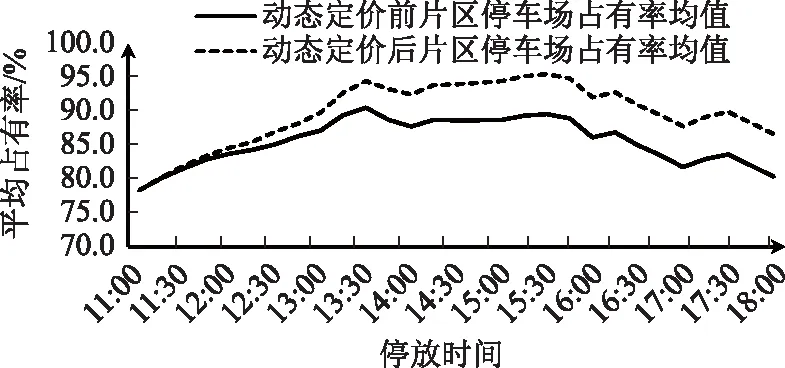
4 结论
