考虑车型与道路线形的山区公路货车事故严重程度影响因素辨识

曹 瑞，戢晓峰，覃文文

(昆明理工大学 交通工程学院，云南 昆明 650504)

0 引言

随着我国物流业的快速发展，公路货运作为物流体系的重要基础，在综合运输体系中发挥着越来越重要的作用。目前，公路货物运输正朝着车辆大型化、重载化、专业化的方向发展，货车保有量不断增加。2018年，我国公路货物运输总量达到395.69亿t，货物周转量71 249.21亿t km，分别占全方式货物运输总量的78.15%和35.73%。随着公路货运量与货车保有量的持续增长，各等级公路的货车混入率也普遍提高。货车在行驶过程中，由于车身体积大、实际载货量高等自身因素影响，以及驾驶员、交通流量、天气、道路几何条件等外部因素的影响容易产生严重的交通事故。近年来，我国道路交通事故数仍然居高不下，其中货车事故占比25%以上，货车事故死亡人数约占道路交通事故死亡总数的39.6%。由此可见，货车事故致死率高，有效的货车事故整治已成为重大现实需求。

同时，受公路设计标准、地形地质条件和建设资金的综合限制，我国山区公路呈现路窄、弯多、坡陡、载货汽车混入率高等特征，行车条件复杂，道路安全性能偏低，导致其交通事故频发且事故严重程度较高。以云南省为例，全省80%的大宗货物在公路上运输，而山区公路线形复杂、转弯半径小且频率高，货车引发交通事故的风险远高于其他公路。据统计，云南省山区公路的交通事故发生率占全部公路的15%以上，货车参与的事故高达20%以上，且人员受伤事故(包含死亡)占比高达35%以上。因此，山区公路复杂的道路线形导致货车事故致死致伤概率更大，迫切需要对山区公路货车事故严重程度影响因素进行分析。

目前，国内外学者从驾驶员特性、车辆特性、行车环境、道路几何条件和事故形态等方面，采用数理统计模型分析潜在的事故影响因素与货车事故严重程度的定量关系，主要针对高速公路与城市快速路，对货车事故严重程度致因进行了分析。从驾驶员角度看，已有研究发现更严重的货车事故与年轻人和老年人、无有效驾驶执照驾驶、超速驾驶以及在酒精或毒品影响下的驾驶有关[1]。Hong等[2]以韩国高速公路事故数据为基础，采用两阶段残差包含估计方法(2SRI)分析了驾驶员违规行为与交通事故发生的内生关系，发现酒后驾驶、嗜睡驾驶、中型或小型货车会增加驾驶员违规行为的可能性，继而增加事故风险。从车辆特性来看，有研究发现更严重的事故伤害与货车载重、车速差异大有关。如胥川等[3]基于新泽西事故数据库，采用Logit和Probit模型估计解释变量对事故严重程度的影响，发现了事故严重程度和货车重量的正相关关系。从环境角度来看，有研究显示更严重的事故与恶劣天气有关[4]，但在路面潮湿情况和照明条件方面的研究结果不一致。如Azimi等[5]采用随机参数有序logit(RPOL)模型分析了驾驶员、车辆、道路和碰撞的各种属性对佛罗里达州际公路货车翻车事故严重程度的影响，发现干燥的路面条件与严重事故相关。从道路角度来看，部分研究关注于弯道路段，当车道宽度更小，没有中央隔离带、纵坡坡度较大的道路条件下更易造成严重事故[6]。Taylor等[7]基于美国某高速公路事故数据，建立负二项式和有序logit货车事故严重程度致因分析模型，发现低肩宽、上坡或下坡路段更容易造成严重事故。从事故形态角度来看，部分研究发现严重事故与侧滑碰撞有关[8]，而撞固定物和追尾碰撞与轻微伤害事故相关[9-10]。还有研究关注了货物类型、货车配置、流量、空间依赖和物流公司特征等方面[11-13]。最近，已有学者开始关注于山区公路行车环境，探讨货车事故严重程度致因。如Wang等[14]以江西省和陕西省4条山区公路上的2 695起重型货车事故数据为基础，采用部分比例优势模型分析几何特征、驾驶员、碰撞、卡车和环境特征对货车事故严重程度的影响，发现异常驾驶行为、年轻驾驶员、坡度较大与更严重的事故后果有关。

综上可知，现有研究在货车事故严重程度致因分析中考虑了较多因素，然而对道路几何特征及货车类型的关注较少，且目前的道路线形指标选取较为单一，未能充分考虑不同道路等级下不同线形组合对货车事故严重程度的影响差异。因此，本研究聚焦车型和线形，基于云南省楚雄州典型山区公路(元双公路元谋-牟定段)货车(轻型、中型、重型)涉事事故数据，建立有序logit模型(OLM)，拟合道路线形组合、曲线半径、外距、纵向坡度和竖曲线类型等道路几何特征因素、驾驶员、碰撞、环境和车型等因素与货车参与事故严重程度的函数关系。根据模型估计结果，辨识影响山区公路货车事故严重程度的显著因素，为山区公路货车事故整治提供参考，对提升我国山区公路交通安全水平具有重要现实意义。

1 数据准备

1.1 数据收集与处理

本研究选取云南省楚雄州典型山区公路(元双公路)K0+000-K87+422路段为研究对象。该路段全长87.42 km，设计速度60 km/h，路基宽8.5 m，为双向两车道，共有159处弯道，平曲线最小半径125 m，其中弯道半径小于500 m的高达117个，弯道路段长46.14 km，占研究路段总长度的52.54%。聚焦山区公路货车事故严重程度致因分析的研究目标，本研究从交警与公路管理部门收集了2012—2017年共2 215起事故数据和道路线形数据。事故原始数据主要包含案情简要、事故发生时间、星期、桩号、天气、路表、路面、事故形态、照明条件、涉事车辆、死亡人数、失踪人数、受伤人数、直接财产损失等字段。道路线形数据由元双公路牟定路段的竖曲表和直曲表构成，主要包含变坡点、竖曲线类型、坡度、坡长、竖曲线长、直线坡长、交点桩号、转角值、曲线半径、曲线长度、缓和曲线长度、切线长度、外距、曲线位置等字段。原始数据为人工收集的全事故数据，存在信息记录不全、有误等现象，因此需要对数据进行处理，提取货车参与事故数据，剔除无效信息，最终形成山区货车事故严重程度致因分析数据库。

山区公路上行驶的车辆有客车、货车、摩托车、自行车、微耕机、拖拉机、电动车、三轮车、装载机等，从元双二级公路2012—2017年2 215起事故数据中可知，单一车辆涉事事故较少，约占20%。本研究将涉事车辆包含货车(轻型、中型、重型)的所有事故作为货车事故研究的原始数据集。然后对原始数据集进行分析处理，最大限度提取出可用字段，再结合竖曲表和直曲表提取事故路段的道路线形数据，形成货车事故严重程度致因分析数据库，为下一步选取模型变量做准备。

1.2 变量选取

1.2.1 因变量选取

交通事故严重程度根据每起事故的伤亡程度及财产损失进行划分，2004年公安部发布《交通事故统计暂行规定》，将交通事故严重程度划分为死亡事故、重伤或轻伤事故和财产损失事故3个等级。本研究参照公安部规定，结合以往相关研究及实地调查的交通事故数据，将事故严重程度划分为财产损失事故、轻微事故、严重事故3类。具体见表1。

表1 山区公路货车事故严重程度划分标准

1.2.2 自变量选取

货车事故的发生是人-车-路-环境等各方面因素作用的结果，本研究在分析国内外现有研究基础上，综合考虑山区公路线形特征，以货车事故严重程度致因分析数据库为基础，最终选取了驾驶员年龄、事故发生时间、天气、货车类型、事故形态、道路线形等13个候选自变量来构建山区公路货车事故严重程度影响因素分析模型。自变量的定义及描述性统计特性见表2。

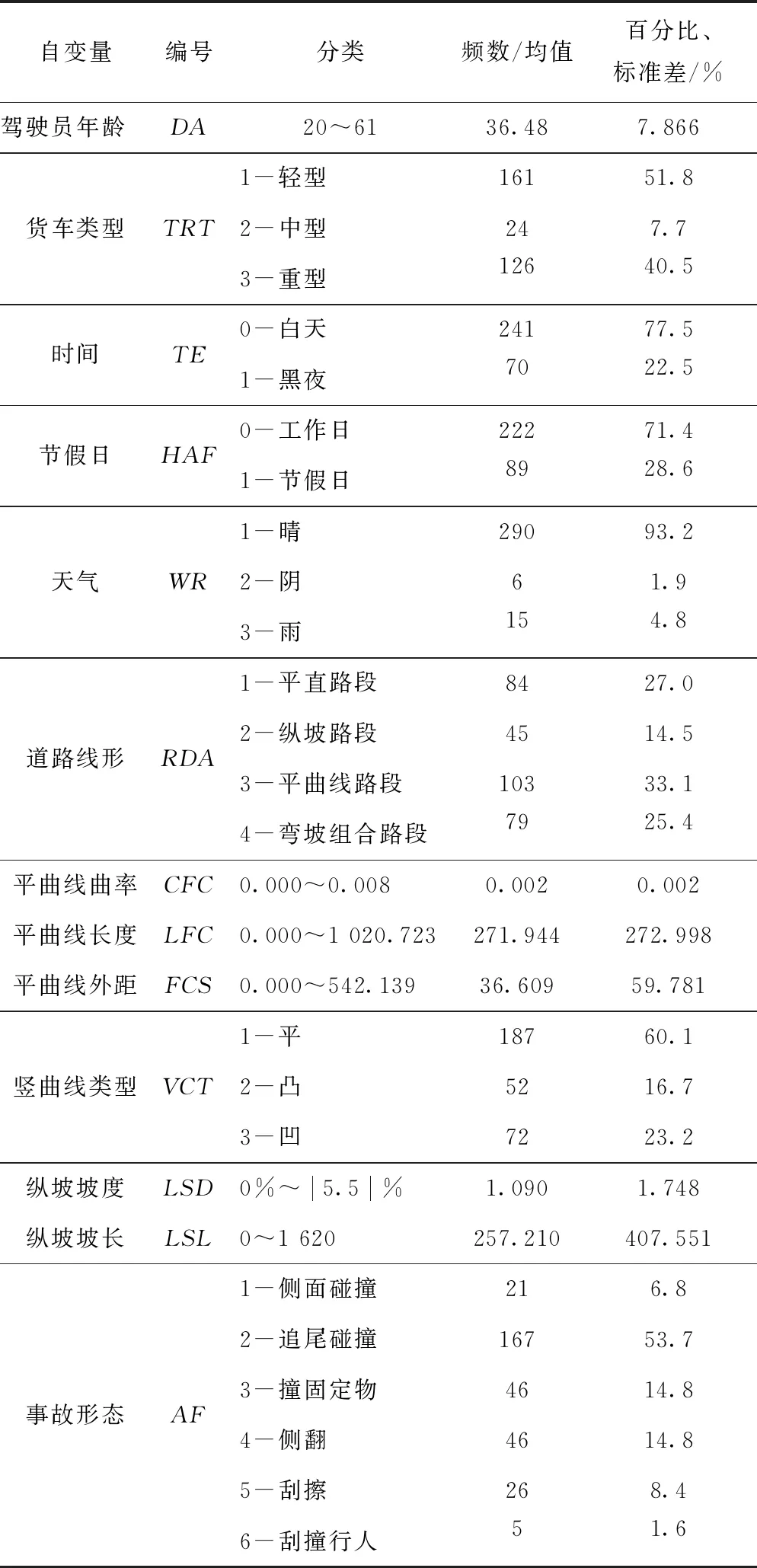
表2 自变量划分标准

13个候选自变量中，有6个连续变量，2个二分类变量和5个多分类变量。对于多分类变量需要设置虚拟变量，若变量含有n(n≥3)个类别，模型中引入n-1个虚拟变量。如TRT分为轻型、中型和重型3类，以轻型为参考类，则引入TRT1和TRT2两个虚拟变量，见表3。

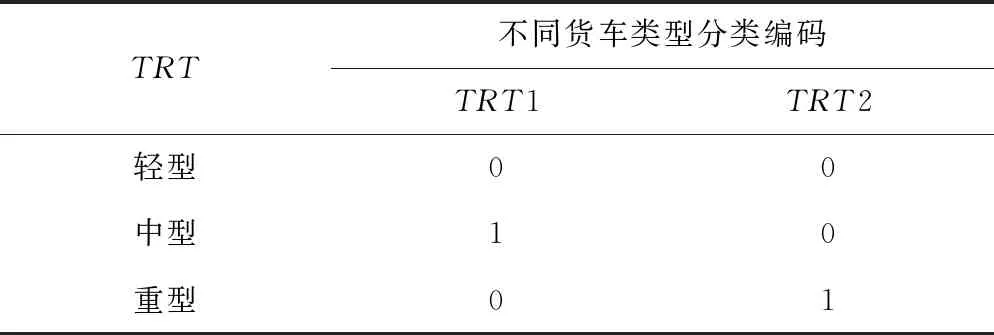
表3 虚拟变量货车类型分类编码

2 研究方法

2.1 模型构建

目前离散选择模型被广泛应用于货车事故的分析与预测研究中，且事故严重程度存在有序特性，其与影响因素并非只是简单的非线性关系，传统的多项logistic不能准确获取事故严重程度与变量之间的关系。因此，本研究采用有序logit模型(OLM)进行山区公路货车事故严重程度致因分析，然后对显著变量进行边际效应估计，从而更好地反映显著自变量对事故严重程度的影响方向和强弱程度。

2.1.1 有序logit模型

有序logit模型主要用于处理因变量为有序的多分类结果，属于二项logit模型的扩展[15]。OLM可表示为：

(1)

式中，P(*)为特定事故严重程度等级的发生概率；Yi为第i(i=1,2,…)起事故的受伤严重程度等级；j为事故严重程度等级(j=1,2,…,M)；X为自变量组成的集合；β为X的系数；αj为第j等级的常数项。由于本研究将事故严重程度分为3类，因此OLM模型为：

(2)

P(Y=2|X)=P(Y≤2|X)-P(Y≤1|X)，

(3)

P(Y=3|X)=1-P(Y≤2|X)。

(4)

2.1.2 边际效应估计

为进一步反映显著自变量对事故严重程度的影响方向和强弱程度，需计算各个自变量的边际效应值。分两种情况来计算：当自变量为二分类变量时，可直接计算该变量的边际效应值[16]如式(5)所示；当自变量为多分类变量时，由于变量可微，故采取弹性分析计算边际效应值[17]如式(6)所示。

(5)

(6)

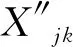
2.2 模型检验

2.2.1 共线性假设检验

OLM前提条件要求自变量之间无多重共线性，即若自变量间存在着较强相关性时，通常情况下认为此模型违背了基本假设。本研究采取相关性分析法和方差膨胀因子法综合诊断自变量间的共线性[18]。方差膨胀因子法通过计算方差膨胀系数(Variance Inflation Factor，VIF)衡量多元线性回归模型中共线性问题，一般建议若方差膨胀因子(VIF)大于等于10，则表明有多重共线性存在，在进行模型运算前应将不满足该假设的自变量剔除。

2.2.2 比例优势假设检验

OLM需要进行比例优势假设检验(又称平行线假设检验)，否则模型的参数估计误差太大，导致模型信度及效度缺乏。平行线假设检验的Wald检验由Brant(1990)提出，因此又称Brant检验[19]。

2.2.3 拟合优度检验

(1)似然比检验

本研究用似然比指数表征似然比检验结果，即比较仅包含常量项的模型与包含所有解释变量的模型之间似然值的相对大小，分别记为L(Mintercept)和L(Mfull)，模型的参数个数为K，其计算公式如式(7)所示，R2越接近0，表示模型拟合程度越高。

(7)

(2)信息准则指标

信息准则指标包含赤池信息量准则(Akaike Information Criterion,AIC)和贝叶斯信息准则(Bayesian Information Criterion,BIC)，二者均是基于熵的概念，衡量模型的复杂度和模型拟合数据的优度。计算方法为：

AIC=2k-2ln(L)，

(8)

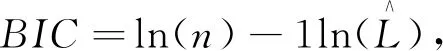
(9)

式中，k为模型中自由参数的数量；L为似然值。AIC和BIC值越小，模型对数据拟合程度越佳。

3 模型结果

3.1 模型演化分析

基于货车事故严重程度致因分析数据库，首先进行共线性假设检验，最终剔除RDA，FCS和LSL3个变量，剩余变量VIF<10均满足要求。运用stata15.0进行回归，取显著性水平为0.100，使用向后剔除变量法，筛选出显著变量，模型演化结果如表4所示。

表4 OLM模型演化

续表4

由表4可以发现，模型M-1到模型M-3演化过程中，AIC和BIC不断下降，说明模型在不断优化。对最终模型M-3进行似然比检验，模型的似然比指数Pseudo-R2为0.028 8，再结合其赤池信息量准则AIC和贝叶斯信息准则BIC分别为465.641和491.820，表明模型的拟合效果较好。采用Brant检验判定最终模型M-3中5个显著自变量是否均满足比例优势假设，结果见表5。

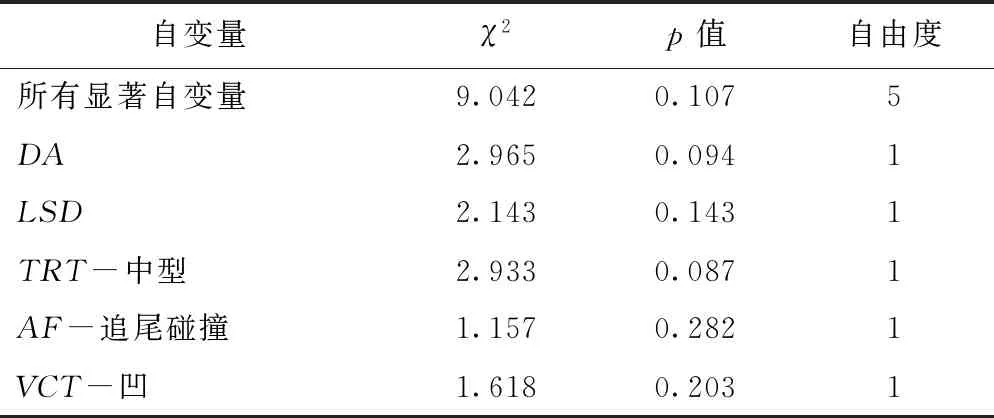
表5 比例优势假设的Brant检验

由表5可知，所有显著自变量的得分检验χ2为9.042，自由度为5，p值为0.107，表明比例优势假设成立。同时，单个自变量的p值均大于0.05，表明在95%置信水平，5个自变量都满足比例优势假设检验。对5个显著自变量进行边际效应估计，结果见表6。

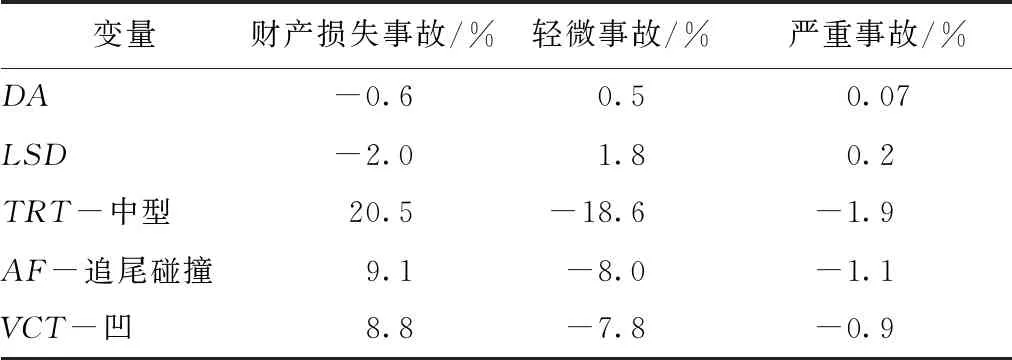
表6 显著自变量对因变量的边际效应

从表4和表6可以发现，DA，LSD，TRT(中型)，AF(追尾碰撞)和VCT(凹)这5个自变量与山区公路货车事故严重程度显著相关。各显著自变量对事故严重程度的影响大小依次排序为TRT，VCT，AF，LSD，DA。

3.2 影响因素分析

3.2.1 道路线形特征

本研究选取道路线形组合(RDA)，平曲线曲率(CFC)，平曲线长度(LFC)，平曲线外距(FCS)，竖曲线类型(VCT)，纵坡坡度(LSD)，纵坡坡长(LSL)7个道路特征变量探讨其对货车事故严重程度的影响机理，通过回归模型最终识别出竖曲线类型和纵坡坡度2个显著变量。其中，纵坡坡度的回归系数为0.107，OR值为1.094，表明坡度越大，货车事故严重程度越高。从边际效应估计结果可知，纵坡坡度与受伤事故显著相关，坡度增加一个单位，货车参与事故的人员受伤概率将增加0.5%，死亡概率将增加0.07%。研究结果与现有研究保持一致，部分研究表明当纵坡坡度大于3%时，事故死亡概率将大幅增加[14]。坡度大的路段会导致驾驶员的视线受阻，同时陡坡将导致重载货车等车辆的爬坡困难以及下坡时的速度上升，这些因素都会导致陡坡路段货车行车安全性的降低。凹型竖曲线的回归系数为-0.534，OR值为0.667，表明凹型竖曲线发生恶性事故的概率低于平面竖曲线和凸型竖曲线。从边际效应估计结果可知，凹型竖曲线与财产损失事故概率的增加(8.8%)和受伤事故概率的适度降低显著相关(-7.8%)。

3.2.2 货车类型特征

事故涉及货车类型(TRT)标记为此事故中涉及的最重货车类型(轻型、中型、重型)。比如，一起事故中同时涉及中型和重型货车，则这起事故的涉及货车类型为重型货车。311起货车事故数据中，被标记为涉及重型货车的事故共126起，被标记为涉及中型货车的事故共24起，被标记为涉及轻型货车的事故共161起，分别占比40.5%，7.7%，51.8%。最终模型并未识别出轻型或重型货车对事故严重程度的影响，研究结果显示，中型货车与财产损失事故概率的增加(20.5%)和受伤事故概率的降低高度相关(-18.6%)。

3.2.3 其他特征

一般而言，回归模型应尽可能控制性别、年龄、归属地等驾驶员特征相关的因素，然而由于采集到的原始数据能提取到的有效变量仅为年龄变量，因此模型最终选取年龄变量进行回归分析。最优模型中年龄的回归系数为0.027，OR值为1.027，表明年轻货车司机(20～61岁)不易造成严重事故。研究结果与现有部分研究不一致，可能是因为未考虑驾驶员不当操作、疲劳驾驶等行为的影响。追尾碰撞事故形态的回归系数为-0.404，OR值为0.668，表明相同条件下，追尾碰撞的事故严重程度低于其他事故形态。从边际效应估计结果可知，追尾碰撞与财产损失事故概率的增加(9.1%)和受伤事故概率的适度降低显著相关(-8.0%)。换言之，与现有研究保持一致的结论是追尾碰撞不太可能导致人员严重受伤，因为追尾碰撞主要造成车辆结构损伤[10]。

4 结论

(1)以货车事故严重程度为因变量，将其分为仅财产损失、轻伤、重伤或死亡事故3个等级，从人、车、路、环境、事故形态5个方面，结合山区双车道公路特点，选取13个候选自变量建立了山区公路货车事故严重程度分析模型。

(2)与山区公路货车事故严重程度显著相关的5个自变量分别为货车类型(中型)、竖曲线类型(凹)、事故形态(追尾碰撞)、纵坡坡度、驾驶员年龄，且5个显著自变量均满足比例优势假设。值得关注的是，本研究发现了山区道路线形特征、货车类型对货车事故受伤率和财产损失率的影响效应。纵坡坡度与货车事故严重程度的正向变动效应说明货车事故整治应重点关注坡度较陡路段。研究结果表明，凹型竖曲线、中型货车类型与财产损失事故概率的增加和受伤事故概率的适度降低显著相关。

(3)分析结果从道路、驾驶员、车辆等角度对山区公路货车事故整治提供了参考。从道路角度看，交通管理部门应对山区公路凹形竖曲线、陡坡等安全隐患路段进行重点排查，加强对此类路段的交通安全监测预警。从驾驶员角度看，针对不同年龄段的货车驾驶员采取差异化措施(提醒驾驶员谨慎驾驶、减少跟驰、超车等)干涉其驾驶行为。从车辆角度看，应重点关注中型货车，及时布控、拦截、查处该类车辆的超载超速等违法行为。

(4)由于数据样本容量有限及人工统计数据等方面的局限性，模型中未能充分体现山区公路环境对货车事故严重程度的影响。因此，获取更精确的山区公路环境、交通流状况等数据，并结合地理空间技术、仿真技术对货车事故影响机理进行深入分析将是下一步研究的重点。