异形纤维阵列过滤特性的数值模拟
2022-02-12王戈孙志伟谭蔚邱威朱国瑞
王戈,孙志伟,谭蔚,邱威,朱国瑞
(1 天津大学化工学院,天津 300350;2 湖南中烟工业有限责任公司,湖南 长沙 410007)
近年来,大气污染的加剧给人体的呼吸系统带来了极大的负担。因此系统性地处理由于人类活动或自然过程排入大气并对环境或人体产生有害影响的颗粒物已刻不容缓;而纤维过滤作为过滤有害成分的成本低廉且有效的方法已经被越来越广泛地应用。
纤维过滤器过滤性能的研究都以单纤维过滤理论为基础,基于Kuwabara和Happel提出的圆柱绕流理论,关于单纤维的绕流特征及其表面粒子捕集的相关研究逐渐发展。之后Davies通过将沉积扩散、直接拦截、惯性碰撞3种过滤作用进行关联,得到了小雷诺数下的纤维过滤实验经验关联式;Friedlander 等又对大雷诺数下纤维上颗粒物沉积形态进行了研究;单纤维过滤理论逐渐得到完善。而随着计算机技术的发展,为了进一步得到颗粒动态运动中实验难以测取的轨迹、瞬时作用力等动态信息,DEM 与CFD 相结合的方法逐渐运用于研究纤维过滤过程。朱小洁通过CFD−DEM耦合方法模拟气−固两相流体通过过滤腔内部的过程,将颗粒的物理参数和纤维介质的结构参数作为变量,研究其对颗粒捕获的影响。Qian等在纤维过滤实验中设计出6种不同的纤维结构,且同样使用CFD−DEM耦合方法研究了纤维结构和颗粒性质对过滤过程的影响。Tao 等通过DEM−CFD耦合研究了圆形截面纤维在前致密阵列、常规阵列、后致密阵列分布下的颗粒堆积规律。然而对于比传统圆形纤维具有更大比表面积、更高机械强度的异形纤维,Wang等研究了单个纤维上效率与其表面积等形态参数的关系。Huang 等分别采用格子Boltzmann 方法和LB−CA 方法模拟了非圆形纤维的压降、颗粒捕集效率及颗粒枝簇的动态变化过程。杨会等用布朗动力学方法研究了方形截面纤维的过滤性能,发现在不同的填充率下,方形纤维的综合过滤性能会发生变化。朱辉等研究了迎风角、长短轴比和填充率等参数对惯性粒子过滤性能的影响。可以发现多数研究主要集中于传统方法下异形单纤维的过滤特性,而对于异形纤维阵列的过滤性能及流动特征还有待研究。
针对上述问题,本文采用CFD−DEM 耦合方法,模拟含尘空气通过异形纤维结构的过程。为了比较不同排布方式下过滤器对球形颗粒的过滤效果,本文从颗粒−颗粒与颗粒−纤维间接触力大小及过滤效率的角度对比了矩形阵列、交错阵列、前密阵列、后密阵列的综合过滤性能。这对优化处理空气中总悬浮颗粒物的过滤过程具有重要工程意义。
1 模型建立
1.1 纤维模型的建立
异形醋酸纤维的尺寸由厂家提供,其中外径为255.8μm,异形度为50%[式(1)],如图1 所示,纤度为100D。

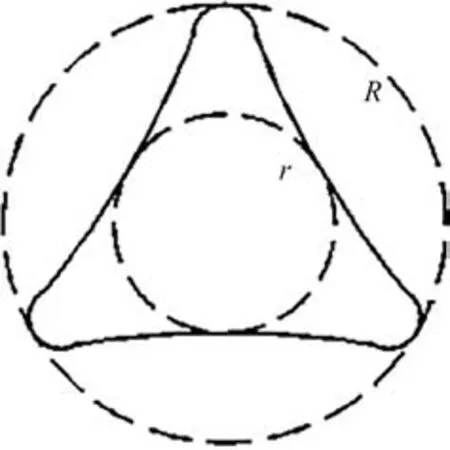
图1 异形纤维截面
1.2 阵列模型的建立
现代过滤理论研究主要依托于两种基础排列,分别是矩形排列以及交错排列,因此首先对这两种排列进行模型构建;矩形纤维阵列及其与过滤腔的组合模型如图2所示。矩形纤维阵列中,30根纤维规则地排成6 列,相邻两根纤维中心的间距为500μm。

图2 矩形纤维阵列及过滤腔
交错阵列纤维模型如图3所示,与矩形纤维阵列模型基本一致,30根纤维丝仍保持6列,且相邻两根纤维的距离保持不变,但第2、4、6列在矩形纤维阵列的基础上竖直移动了250μm。

图3 交错纤维阵列
以交错阵列为基础,保持纤维体积分数不变,改变其疏密结构。如图4所示,前密后疏阵列中前3 列的列距为350μm,后3 列的列距为600μm;前疏后密模型的纤维排布则完全相反。此外,对该模型进行了网格划分及网格独立性检验,网格数6011286。

图4 两种交错纤维阵列的排布
1.3 CFD-DEM数学模型
1.3.1 流体相
在计算流体力学模型中,气相通过连续性和动量守恒方程求解[式(2)、式(3)]。
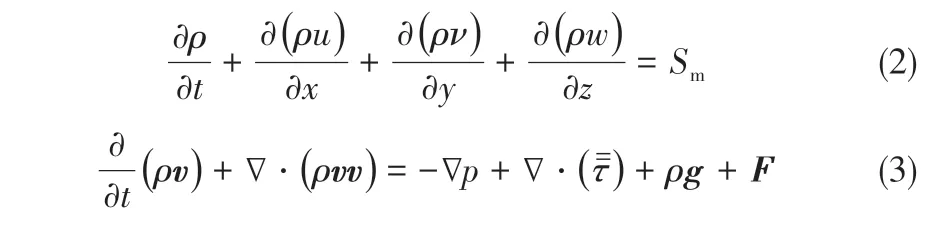
1.3.2 固相
接触模型的选取是否合适对数值模拟结果的准确性有重要影响。经典的Hertz 接触模型仅考虑了弹性变形,而未考虑颗粒间的黏结力,所以并不适合在本文中模拟颗粒−颗粒和颗粒−纤维的接触。而JKR(Johnson−Kendall−Roberts)模型基于三种假设(即:①不考虑材料的塑性和黏弹性小变形,只关心材料线弹性性质;②黏附力的作用范围远小于表面位移;③接触区尺寸远小于接触体尺寸,所以基底可以认为是半无限大空间),在Hertz理论的基础上考虑了表面黏结力对固体弹性形变产生的影响。因此用表面能来表示颗粒之间的相互吸引力的JKR 模型适用于药粉等粉体颗粒和农作物、矿石、泥土等含湿物料,研究颗粒间因静电力、含湿等原因发生明显的黏结和团聚。
本文使用“Hertz−Mindlin with JKR”接触模型,其中Hertz 理论中的颗粒碰撞机制如图5 所示,在此基础上添加了颗粒间黏结力对颗粒运动规律的影响,适用于颗粒间发生明显团聚的情况。

图5 颗粒接触力
切向力主要取决于切向重叠量和切向刚度[式(4)~式(6)]。
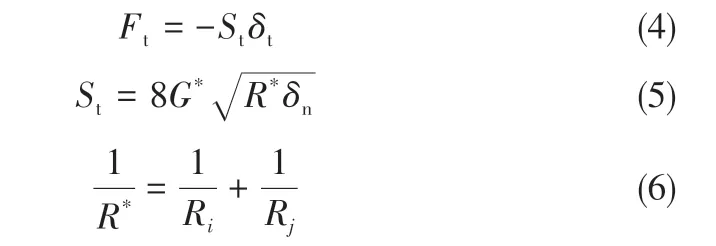
切向耗散力如式(7)~式(9)。

法向力取决于法向重叠量和相互作用的参数表面能[式(10)~式(12)]。
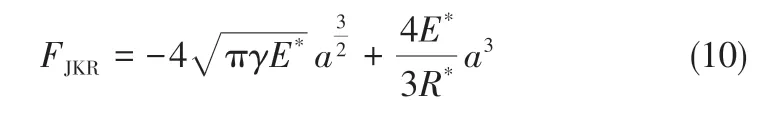
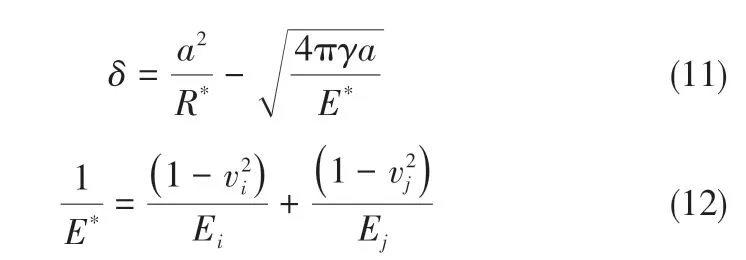

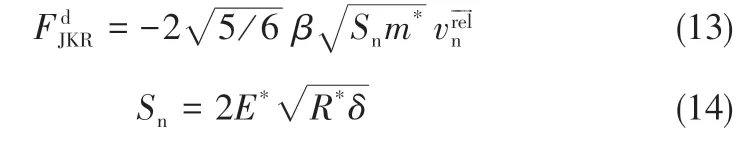
1.4 边界条件
本文采用CFD−DEM 耦合的方法来进行模拟。选用−湍流模型,流体类型为空气,入口边界条件设置为速度入口型,流速大小0.38m/s。模拟总悬浮颗粒物的拦截过滤过程,因此将颗粒的粒径设置为100μm,颗粒生成速度5000个/s,颗粒−颗粒、颗粒−纤维接触模型为JKR 接触模型,颗粒材料和纤维材料的具体设置参数详见表1和表2。

表1 颗粒与纤维物理参数

表2 颗粒与纤维相互作用参数
2 模拟结果与分析
2.1 阵列过滤效果对比
矩形纤维阵列数值模拟中4个时刻下纤维过滤颗粒的效果如图6所示。从图中可以看出,在初始过滤阶段,颗粒的流动较为自由,大部分颗粒在经过流域时与纤维阵列发生碰撞被捕集,在纤维的迎风面产生堆积,而少部分颗粒则从纤维阵列的周围或者阵列的间隙通过。随着过滤进程的推进,更多的颗粒附着到纤维的表面而停止运动,其中颗粒主要在第1列纤维上迅速堆积,少量分布于远离迎风面的一侧,到0.2s时,纤维的间隙已基本被堵塞。
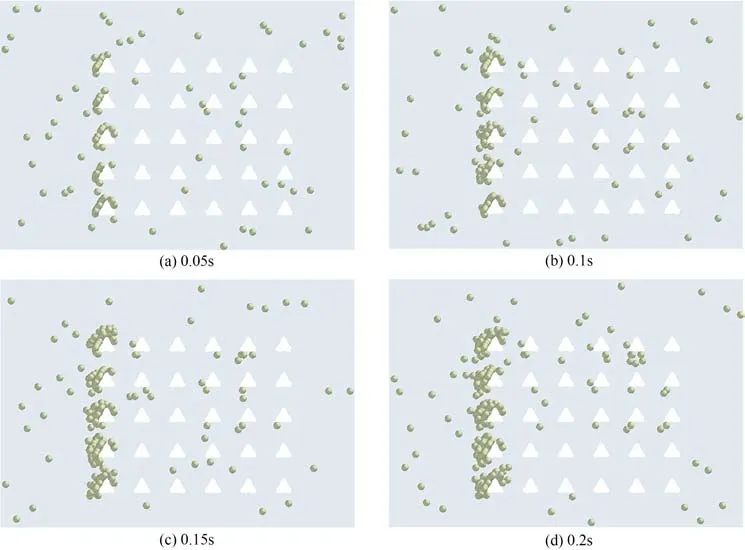
图6 不同时刻下矩形纤维阵列的过滤效果
交错纤维阵列模型在4个时刻下的过滤效果如图7 所示。从图中可以看出,将矩形阵列的第2、4、6 列在竖直方向移动250μm,交错纤维阵列在过滤过程中的颗粒沉积特征与矩形纤维阵列产生明显的差异。在交错纤维阵列过滤的过程中,前两列纤维对颗粒均会存在较为明显的拦截作用。在0.2s时,交错阵列相比矩形阵列截留捕获的颗粒更多。对于矩形阵列,颗粒的截留捕获主要来源于第1列纤维的贡献,只有少数的颗粒会被其他列纤维拦截;交错阵列中对于颗粒过滤起主要作用的则为前两列纤维。

图7 不同时刻下交错纤维阵列的过滤效果
前密阵列和后密阵列的颗粒过滤效果如图8和图9所示,可以发现在0.05s、0.1s时,过滤效果较为相近。但在0.15s 时,后密阵列的第1 列纤维已完全发生堵塞,且前两列纤维上捕获的颗粒相互孤立;而前密阵列则是通过前两列纤维上的颗粒相互联结形成堵塞。
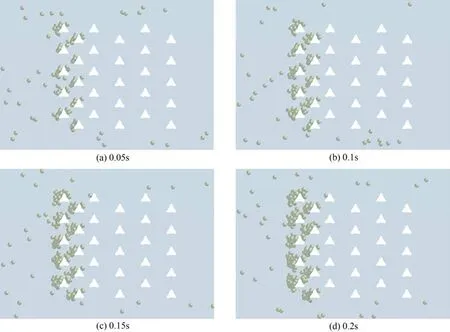
图8 前密阵列的过滤效果

图9 后密阵列的过滤效果
不同接触间法向力随时间的变化如图10所示。无论矩形阵列还是交错阵列,颗粒与颗粒的法向力均小于颗粒与纤维的法向力,如图10(a)所示;说明在0.2s 内,颗粒的堆积更倾向于发生在纤维上,而且颗粒与纤维之间的接触更为牢固;对于颗粒与纤维之间的接触而言,交错阵列上的法向接触力相对更大,反映出交错阵列上的过滤作用强于矩形阵列。结合图10(b)进行分析,两种致密化方式不同的阵列上颗粒与颗粒之间的接触力上同样保持相近水平;而前疏后密阵列上颗粒与纤维间的接触力相较前密后疏阵列略高,但超出程度不大,这表明在两个阵列上纤维对颗粒的吸附作用相当。

图10 不同接触间法向力随时间变化曲线
不同阵列上过滤颗粒数目的对比如图11所示,可以看出过滤的颗粒数目均呈线性快速增长,相同的时间内交错纤维阵列能够过滤更多的颗粒,而前密阵列与前疏阵列的过滤效果则基本保持一致。如图12(a)所示在过滤初始阶段,矩形与交错阵列的过滤效率均会快速提升,随后交错阵列的过滤效率保持在75%左右,而矩形阵列的过滤效率约保持在45%,这反映出交错阵列具有良好的过滤性能;对比图12(b)中的过滤效率可以发现,前密阵列与后密阵列的过滤能力相近。

图11 过滤颗粒数对比
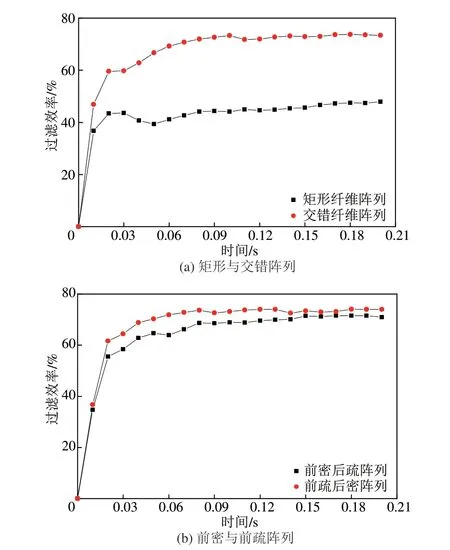
图12 过滤效率对比
品质因数作为衡量过滤器优劣的重要参数,可通过式(15)获得。

如图13 所示品质因数随时间逐渐下降,这是因为随着颗粒的逐渐堆积,可流动空间逐渐被压缩,流动阻力越大,这不利于过滤的发生,因此要保持纤维清洁以维持较高的过滤性能。其次在保持具有较高过滤效率的交错结构基础上,前密后疏的阵列具有相对更好的过滤性能,即在具有较高过滤效率的同时,还能保持较低压降。

图13 品质因数随时间变化曲线
2.2 不同阵列流场变化情况对比
通过建立垂直于模型轴并位于中点的监视面,可以得到压力分布云图。不同时刻下矩形纤维阵列和交错纤维阵列的流场压力分布如图14和图15所示,可以看出,在流体通过过滤腔的过程中,入口处的压力明显高于出口,呈现阶梯状分布且分布特征基本不随过滤进程的推进而变化。
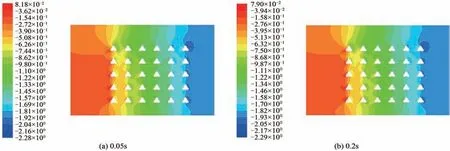
图14 矩形阵列过滤过程压力云图

图15 交错阵列过滤过程压力云图
不同时刻下前密与后密阵列流场中压力的分布情况如图16 与图17 所示。对比入口段与出口段的压力分布可以看出,流体通过前密阵列模型的压降小于流体经过后密阵列模型的压降,这不仅由纤维排布方式的不同造成,更有颗粒堆积和分布状态的原因。

图16 前密阵列过滤过程压力云图

图17 后密阵列过滤过程压力云图
3 结论
本文建立了异形纤维阵列过滤模型,以CFD−DEM 耦合方法在仿真软件中分别进行了相同纤维体积分数下不同排布方式纤维阵列过滤过程的数值模拟,通过对过滤过程中颗粒堆积状态和过滤结果数据的分析对比,得出了如下主要结论。
(1)对比矩形纤维阵列与交错纤维阵列的过滤过程,交错阵列更早进入堵塞阶段且过滤效率高出35%,更适应工程中空气过滤的需要。
(2)对比前密阵列与后密阵列,两者的过滤效果相近,大约都保持在80%,但表现出了不同的颗粒沉降特征。虽然颗粒的拦截均发生在前两列纤维,但当颗粒进入堵塞阶段后,前疏阵列的过滤作用主要发生在第1列纤维,而前密阵列则由前两列纤维共同完成颗粒过滤;拦截相同数量的颗粒时,流体流经后密阵列的压降高于前密阵列。以品质因数对该过滤过程进行表征,前密后疏阵列具有更好的过滤性能。
(3)在整个过滤过程中,从法向力的角度进行分析,对于过滤的贡献主要来源于纤维对颗粒的拦截,且拦截作用要更为牢固,已经被纤维吸附拦截的颗粒更不易发生脱落。
符号说明
—— 异形度
—— 过滤效率
—— 等效杨氏模量,Pa
—— 恢复系数
—— 外力或相关模型源项
—— 当量剪切模量,Pa
—— 等效质量,kg
—— 静压,Pa
Δ—— 压力降,Pa
—— 外接圆半径,μm
R—— 接触圆半径,m
—— 等效半径,m
—— 内切圆半径,μm
—— 质量源项
—— 法向刚度
—— 时间,s
υ—— 泊松比
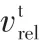
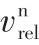
—— 应力张量
—— 流体密度,kg/m
—— 静摩擦系数
t—— 切向
n—— 法向
