结构化图形在几何单元复习课设计中的应用探索

马学三

一、 研究的缘起

(一)中考几何复习教学现状

纵观目前几何单元复习教学现状，教师普遍采用的是以下三种常态几何复习教学模式。

模式1：完全按照《复习用书》，主要形式是“N+1+X”，先完成“N”个与本单元相关的课前测题目，再梳理“1”张知识表或知识图，最后完成“X”种类型题。

模式2：选择使用《复习用书》，主要形式是“1+X+1”，先回顾梳理“1”张本单元几何概念、性质和判断知识图表，再完成“X”种类型题，最后完成“1”个综合拓展问题。

模式3：完全自编复习教案，主要形式是“1+X”，围绕“1”个单元基本图形设计“1”个典型习题，通过变式拓展“X”个问题串，称为“一题一课”复习课型。

第一、二种常规的几何复习教学模式，注重几何知识和对应问题的归类讲解，缺少知识单元整体深度学习结构的系统构建，因此学生忙于刷题，解题能力提升不大，而且不能激发学生的复习兴趣。第三种几何复习教学模式，是目前比较认可的效率较高的方法，通过以典型题(图)促发单元重点知识回顾，并通过变式形成研究的基本结构，这种方式比前面两种方式效果好，但是也存在典型题(图)选择不精准情况，需要教师课前精心设计。

(二)中考几何答题情况现状

近几年的杭州市中考压轴题都以圆为背景、考查圆内直线的基本结构图形，从学生的答题情况分析，对基本结构图形的认识和分析能力较弱，知识存储都是以单一线性为主，特别像2021年的第23题第③小题，有19%左右的学生不会做。

(2020年)如图1，已知AC，BD为⊙O的两条直径，连接AB，BC，OE⊥AB于点E，点F是半径OC的中点，连接EF。连接BF，DF，设OB与EF交于点P，①求证：PE=PF。②若DF=EF，求∠BAC的度数。

图1

(2021年)如图2，锐角三角形ABC内接于⊙O，∠BAC的平分线AG交⊙O于点G，交BC边于点F，连接BG。

图2

①②略。③已知点E在线段AF上(不与点A，点F重合)，点D在线段AE上(不与点A，点E重合)，∠ABD=∠CBE，求证：BG2=GE·GD。

(三)教研室几何单元复习指导建议

1.要重视几何复习素材来源于教材和真题。

2.要重视几何知识单元整体在建构知识结构过程中，梳理知识框架体系，通过典型图形的主题学习，掌握单元核心内容并形成较为熟练的学习和思维结构。

基于以上背景，以几何知识单元典型结构性图形为复习素材和载体，设计好链式和环式问题促进学生形成良好的知识结构，再对结构性图形进行变式，发展学生的认知和思维结构，从而提升几何复习的效果，这是解决当前初中几何单元复习效率低的有效途径，本课题进行了教学设计和具体操作实施的研究。

二、 研究的设计

(一)概念的界定

结构化图形：在几何知识单元复习中，一种是基于知识系统的结构化基本图形，另一种是基于典型综合问题的结构化组合图形。

在几何知识单元复习中，依托单元结构化基本图形，整体分层设计具有链式+环式的结构化问题。

在几何知识单元复习中，培养学生利用单元结构化基本图形和问题重构研究内容，建立学习路径。

在几何知识单元复习中，引导学生用系统思维的方法完整、深刻地研究图形和问题，从而使学生形成相对固定的结构化思维。

(二)研究的思路

几何知识单元的复习，必须在单元教学观下进行，复习课是对知识单元的总结、反思和提升，不仅仅是经典题的再回顾，不只是梳理知识点，而是要让学生有新的收获，几何单元复习课的功能与目标应是多元的：数学知识的整合与理解、方法策略的建构与内化、思维能力的形成与提升，不局限于本章节，而应在整个初中数学知识系统中，让学生感知本章节的地位与作用，体会本章节与前面章节和后面章节的联系。

(三)研究的路径

本课题的研究从“一路径·两结构”研究几何知识单元教学设计与实施。

一路径：几何知识单元复习结构化学习路径。

两结构：结构化图形和结构化问题串。

研究程序如下框图。

通过设计—实施—改进—再实施，基本形成几何知识单元复习教学模式的研究。

(四)研究的目标

1.总体目标

通过本课题的研究，有效提高了几何单元复习的教学效率，提高了学生几何结构化深度学习能力，很好地发展了学生几何结构化系统思维。

2.细化目标

(1)通过本课题研究掌握了几何知识单元划分的基本原则；(2)通过本课题研究掌握了几何知识单元结构化图形和问题的设计能力；(3)通过本课题研究，学生基本学会了几何知识单元复习的结构性学习路径；(4)通过本课题研究，基本形成了几何知识单元复习教学设计及操作模式。

三、 研究的内容

(一)几何知识单元复习课的结构化知识内容设计

结构性知识单元的划分原则：聚焦同一类研究对象，包含对象概念、要素、性质、判定和运用等自成一个闭环逻辑体系。本课题划分原则按照1课时的知识单元内容。

(二)结构化作图或问题串：几何知识单元复习课引入阶段的设计

1.通过结构化作图串，重构知识单元结构

根据划定知识单元的内容特征，及学生获取几何新知识的方法，部分几何单元可以通过设计结构化作图串重构知识单元结构，并形成结构化的基本核心图形。

在复习《直线与圆的位置关系》单元时，设计如下作图任务串。已知在△ABC中，∠ACB=90°，AC=3，BC=4。

①以C为圆心，4为半径的⊙C与直线AB的位置关系。

②若直线AB与半径为r的⊙C相切，求r的值。

③求作圆心在BC边上的⊙O。

④求作过点C的⊙O。

⑤求作与直线AB相切的⊙O。

2.通过结构化问题串，重构知识单元结构

根据划定知识单元的内容特征，及学生获取几何新知识的方法，部分几何单元可以通过一个基本图形设计结构化问题串，重构知识单元结构，并形成结构化的基本核心图形。

在复习《特殊三角形》单元时，设计如下问题串。已知，在△ABC中，AB=AC，请回答以下问题。

①若两边长分别为2和3，则△ABC的周长为。

②若∠B=75°，则∠BAC=；若∠BAC=30°，则∠C=。

③若点D是BC边中点，AB=10，BC=12，则AD=；若点E是AB中点，则DE=；

若CF⊥AB，则CF=；若AP平方∠DAB，则DP=。

④如果AB=13，BD=5，AD=12，则△ABD为三角形。

⑤若点D是BC边中点，点F是AB上一点，DF=BF，则△ADF是三角形。

(三)结构化基本核心图形：几何知识单元复习的图形归纳

罗增儒教授指出，教材是中考命题的基本依据，教材内容是中考复习资源的基本来源。因此根据划定的知识单元，归纳出相应的结构化基本核心图形是学生重构知识结构的重要载体。

1.通过教材中蕴含的概念、性质和判定图形，归纳出结构化基本核心图形

学习九上3.3垂径定理和3.4圆心角定理时，总结出基本图形，加深直观理解。(如图3)

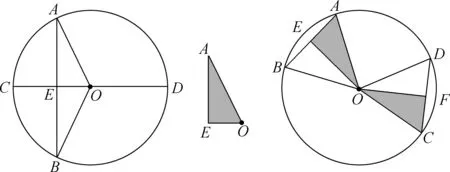
图3

通过总结基本图形，不仅能够使学生知道切线长定理的内容，更能使学生知道和理解该定理的证明过程，以及由此基本图形推导得出的其他结论。

学习九下2.2切线长定理时，总结出基本图形。(如图4)

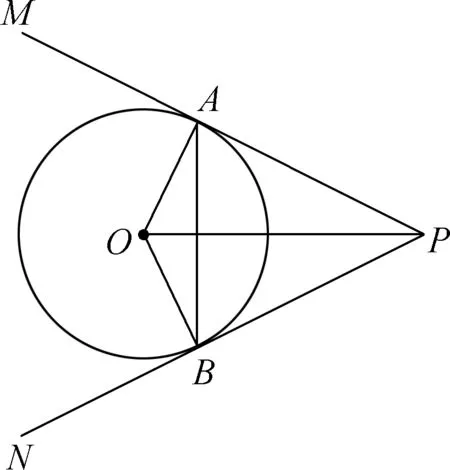
图4

通过总结基本图形，不仅能够使学生知道垂径定理和圆心角定理的内容，同时也能使学生对该定理的推理过程有直观显性的理解载体，由基本图形构建知识网络，提高学习的效率，锻炼学生的几何思维能力。

2.通过教材例题和习题中的图形，归纳出结构化基本核心图形

在复习九上相似三角形单元时，归纳六种基本图形。(如图5)

图5

通过总结归纳六种相似三角形的结构化基本图形，可以加深学生对图形中边和角对应关系的理解，学生可以在一些复杂的相似三角形图形中快速准确地找到相似三角形。

利用九上4.5相似三角形的性质及应用(3)作业题5：

有一块三角形余料ABC，它的边BC=120mm，高线AD=80mm。要把它加工成正方形零件，使正方形的一边在BC上，其余两个顶点分别在AB，AC上。求加工成的正方形零件的边长。(如图6)

图6

这个基本图形用到相似三角形对应边上的高之比等于相似比的性质，作为性质应用的结构化基本核心图形，涉及的知识也是相似三角形的重要性质，学生熟练掌握这个图形与性质，能够简化解决类似几何问题的思考过程。

利用九下1.3解直角三角形(3)作业题3：

如图7，广场上空有一个气球A，地面上点B，C，D在一条直线上，BC=20m。点B，C分别测得气球A的仰角∠ABD为45°，∠ACD为56°。求气球A离面的高度AD(精确到0.1m)。

图7

这个基本图形用到解直角三角形和三角函数知识，图中是两个含有公共直角边的直角三角形，图形比较典型，根据条件一般不能直接解决其中任意一个三角形问题，只能通过设未知数x的间接方法来解决问题。因此这是一个图形和方法都比较典型的问题，作为本章一个重要的结构化基本核心图形让学生积累。

(四)中考复习几何知识单元的结构化变式问题链设计

传统的复习课很容易变成单纯的习题课，做完一题又开始下一题，题做了不少，其中也不乏好题，但是涉及过多导致整节课零散，知识和技能重复，不仅效率低下，而且增加学生负担，与现在要求的“双减”相悖，深层次原因是问题没有体现结构化层次性，导致学生没有形成学习结构和思维结构。本课题从以下但不局限于这几种方法研究结构性变式问题链设计。

1.分析和探究中考试题，设计结构化问题链

如杭州市2019年中考题：

23.如图，已知锐角三角形ABC内接于⊙O，OD⊥BC于点D，连结OA。

(1)若∠BAC=60°，

②当OA=1时，求△ABC面积的最大值；

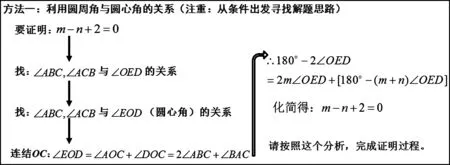
(2)点E在线段OA上，OE=OD。连接DE，设∠ABC=m∠OED，∠ACB=n∠OED(m，n是正数)。若∠ABC<∠ACB，求证：m-n+2=0。

设计如下图两种结构化问题链：

如杭州市2017年中考题：

23.如图，已知△ABC内接于⊙O，点C在劣弧AB上(不与点A，B重合)，点D为弦BC的中点，DE⊥BC，DE与AC的延长线交于点E，射线AO与射线EB交于点F，与⊙O交于点G，设∠GAB=α，∠ACB=β，∠EAG+∠EBA=γ。

(1)点点同学通过画图和测量得到以下近似数据：

α30°40°50°60°β120°130°140°150°γ150°140°130°120°

猜想：β关于α的函数表达式，γ关于α的函数表达式，并给出证明；

(2)若γ=135°，CD=3，△ABE的面积为△ABC的面积的4倍，求⊙O半径的长。

设计如下图结构化问题链：

2.研究和拓展中考图形，设计结构化图形串

如杭州市2020年中考题：

已知AC，BD为⊙O的两条直径，连接AB，BC，OE⊥AB于点E，点F是半径OC的中点，连接EF。连接BF，DF，设OB与EF交于点P，①求证：PE=PF。②若DF=EF，求∠BAC的度数。

通过分析研究，挖掘并拓展基本图形(图8)，形成结构化图形。

图8

(五)几何单元复习的结构化典型组合图形设计

几何综合性问题往往隐含不止一个结构化基本图形，通过变式问题链的设计，建构成结构化典型组合图形，通过这方面的学习，学生在建构过程中，不仅经历了组合图形的产生过程，也建构了复杂图形的一般研究路径，从而促进学生应用结构化图形解决问题意识的培养。

四、 结语

几何解题能力是数学的基本能力，是形成几何直观核心素养的重要体现，通过几何单元复习的教学实践，利用结构化图形和问题，使学生在形成几何结构化知识体系时，能够形成基本的结构化研究路径，并用图形承载知识，有效发展学生的几何能力。本研究对当前学生几何直观、几何解题能力普遍薄弱的现状有一定的积极作用，笔者将继续进行后续跟几何图形相关的教学研究。