RESEARCH ANNOUNCEMENTS ON“UPPER BOUND ESTIMATES OF EIGENVALUES FOR HRMANDER OPERATORS ON NON-EQUIREGULAR SUB-RIEMANNIAN MANIFOLDS”
2022-02-11CHENHuaCHENHonggeLIJinning
CHEN Hua,CHEN Hong-ge,LI Jin-ning
(1.School of Mathematics and Statistics,Wuhan University,Wuhan 430072,China)
(2.Wuhan Institute of Physics and Mathematics,Innovation Academy for Precision Measurement Science and Technology,Chinese Academy of Sciences,Wuhan 430071,China)
1 Introduction and Main Results
For n≥2,let M be a n-dimensional connected smooth manifold.We take a fixed smooth measure on M with strictly positive density,and write dx as the measure when we integrate.Also,we simply denote the measure of a set E⊂M by|E|.
Suppose that X=(X1,X2,···,Xm)are the real C∞vector fields defined on M,which satisfy the so-called Hrmander’s condition with Hrmander’s index Q:there exists a smallest positive integer Q such that these vector fields X1,X2,...,Xmtogether with their commutators of length at most Q span the tangent space at each point of M.
Starting from the vector fields X=(X1,X2,···,Xm)which satisfy the Hrmander’s condition,we can construct a sub-Riemannian manifold(M,D,g)endowed with the canonical sub-Riemannian structure(D,g),where the distribution D is a family of linear subspaces Dx⊂ Tx(M)such that Dx=span{X1(x),X2(x),···,Xm(x)}depending smoothly on x∈M,and the sub-Riemannian metric g:TM → R∪{+∞}is a function given by g(x,v)=for x ∈ M and v ∈ Tx(M).Observe that g(x,·)is a positive de finite quadratic form on Dxand g(x,v)=+∞for vDx.
For each x∈M,the sub-Riemannian flag at x is the sequence of nested vector subspaces
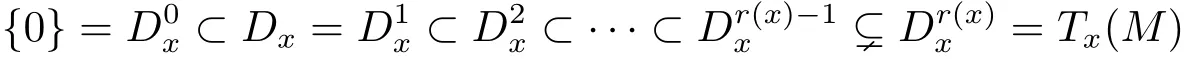
defined in terms of successive Lie brackets,and r(x)≤Q is the degree of nonholonomy at x.Here for each 1≤j≤r(x),is the subspaces of the tangent space at x spanned by all commutators of X1,...,Xmwith length at most j.Setting νj(x)=dimfor 1 ≤ j ≤ r(x)with ν0(x):=0,the integer
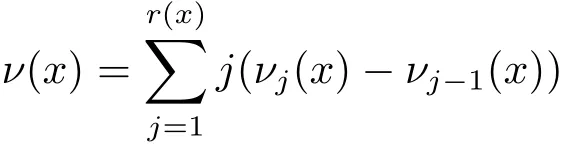
is called the pointwise homogeneous dimension at x.Besides,a point x∈M is regular if,for every 1 ≤ j ≤ r(x),the dimension νj(y)is a constant as y varies in a open neighborhood of x.Otherwise,x is said to be singular.A set S⊂M is equiregular if every point of S is regular.The set S⊂M is said to be non-equiregular if it contains some singular points.The equiregular assumption in sub-Riemannian geometry is also known as the M´etivier’s condition in PDEs.For an equiregular connected set S,we know that the pointwise homogeneous dimension ν(x)is a constant ν which coincides with the Hausdorff dimension of S related to the vector fields X,and this constant ν is also called the M´etivier’s index.Furthermore,if the set S ⊂ M is non-equiregular,we can introduce the so-called generalized M´etivier’s index by

In this paper,we concerned with the eigenvalue problems of self-adjoint Hrmander operatoron non-equiregular sub-Riemannian manifolds,wheredenotes the formal adjoint of Xi.Precisely,we first study the closed eigenvalue problem of-△X,i.e.

where M is a n-dimensional connected compact smooth manifold without boundary.Secondly,we study the Dirichlet eigenvalue problem of-△X.For simplicity we assume that M is an open connected domain inendowed with Lebesgue measure,and Ω ⊂⊂ M is a bounded connected open subset with smooth boundary∂Ω which is non-characteristic for X=(X1,X2,···,Xm).The Dirichlet eigenvalue problem of-△Xwill be considered as follows
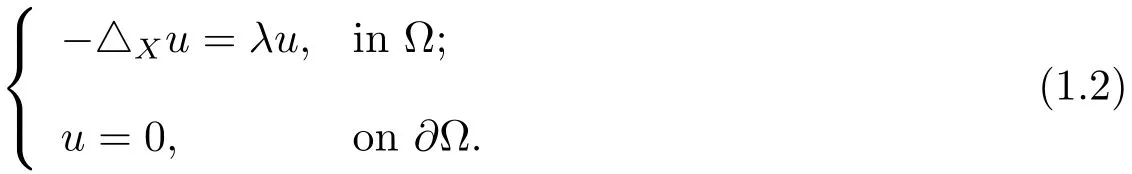
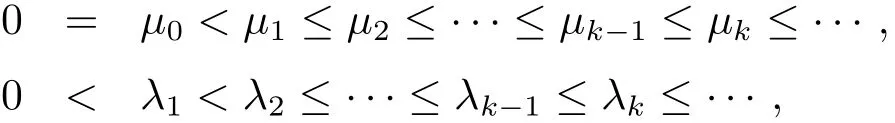
Combining the Rayleigh-Ritz formula with Jerison and S´anchez-Calle’s subelliptic heat kernel estimates in[6,8],we can obtain the following estimate for closed eigenvalue problem(1.1).
Theorem 1.1Let X=(X1,X2,···,Xm)be the C∞real vector fields defined on the compact manifold M,which satisfy the Hrmander’s condition in M.Denote by μkthe ktheigenvalue of the problem(1.1).Then for any 0<t<1 and any k≥0,we have

Remark 1.1From Theorem 1.1,we can recover the lower bound estimate of the counting function given by Fefferman and Phong in[4],namely

holds for sufficient large λ > 0,where N(λ):=#{k|μk≤ λ}is the spectral counting function and c1>0 is a constant depending on the sub-Riemannian structure.This means(1.3)possesses the optimal growth order.

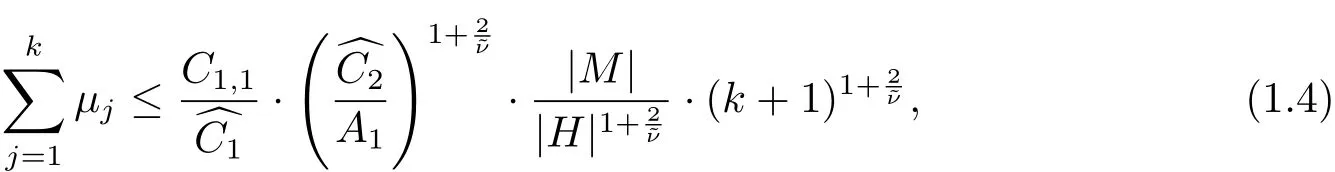
and


Furthermore,we can also obtain the following inequality for the Dirichlet eigenvalues of the problem(1.2).
Theorem 1.3Let X=(X1,X2,···,Xm)be C∞real vector fields defined on a connected open domain M in,which satisfy the Hrmander’s condition.Assume that Ω ⊂⊂ M is a bounded connected open subset with smooth boundary such that ∂Ω is noncharacteristic for X.Denote by λkthe ktheigenvalue of the problem(1.2).Then for any compact subset K ⊂ Ω,there exists a positive constant δ(K),such that for any 0 < t≤ δ(K)and any k≥1,we have

where A2and A3are some positive constants which depend only on the sub-Riemannian structure.
Similarly,when the subset H has a positive measure,Theorem 1.3 also indicates the following explicit upper bounds of λkwhich are optimal in terms of the order on k,and also compatible with the asymptotic results in[2].


and
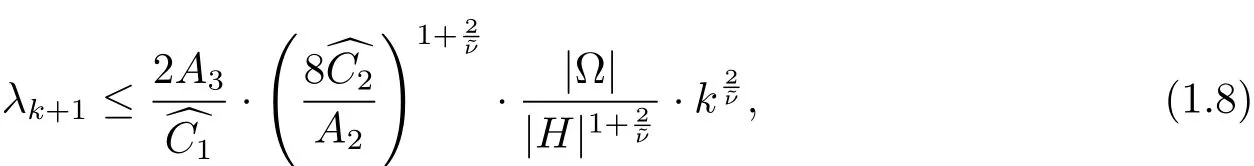
The details of proofs for Theorem 1.1–Theorem 1.4 have been given in[3].
杂志排行
数学杂志的其它文章
- RESEARCH ANNOUNCEMENTS ON“MODERATE DEVIATIONS FOR GRENANDER ESTIMATOR NEARBOUNDARIES OF THE SUPPORT”
- ON REFINED YOUNG’S REVERSE INEQUALITIES FOR POSITIVE LINEAR OPERATORS
- SYMPLECTIC CRITICAL SURFACES WITH CIRCULAR ELLIPSE OF CURVATURE IN TWO-DIMENSIONAL COMPLEX SPACE FORMS
- STUDY ON 2-DIMENSIONAL SUBMANIFOLDS WITH CONSTANT DETERMINANT OF BLASCHKE TENSOR
- THE SPREADING SPEED FOR A NONLOCAL DIFFUSIVE PREDATOR-PREY MODEL WITH ONE PREDATOR AND TWO PREYS
- ON SPLIT REGULAR BIHOM-LIE COLOR ALGEBRAS
