SYMPLECTIC CRITICAL SURFACES WITH CIRCULAR ELLIPSE OF CURVATURE IN TWO-DIMENSIONAL COMPLEX SPACE FORMS

HE Ling,TIAN Ting-yu

(Center for Applied Mathematics,Tianjin University,Tianjin 300072,China)

Abstract:We study the symplectic critical surfaces in two-dimensional complex space forms with the property that the ellipse of curvature is always a circle.By using the method of moving frame,we prove that such surfaces are minimal.The results enrich the contents of symplectic critical surface.

Keywords: symplectic critical surfaces;ellipse of curvature;minimal surfaces;complex space forms

1 Introduction

An interesting notion that comes up in the study of surfaces in higher codimension is that of the ellipse of curvature.This is the image in the normal space of the unit circle in the tangent plane under the second fundamental form.

Using this concept,Guadalupe-Rodriguez(cf.[1])obtained some inequalities relating the area of compact surfaces in(real)space forms and the integral of the square of the norm of the mean curvature vector with topological invariants.When the ellipse of curvature is a circle,restrictions on the Gaussian and normal curvatures gave them some rigidity results.

Castro(cf.[2])classified the Lagrangian orientable surfaces in complex space forms with the property that the ellipse of curvature is always a circle.As a consequence,they obtained new characterizations of the Clifford torus in the complex projective plane and of the Whitney spheres in the complex projective,complex Euclidean and complex hyperbolic planes.

Other works which use the ellipse of curvature as a tool in the study of surfaces in(real)space forms can be found in these articles.(cf.[3–5])

In this article we attach the circular ellipse of curvature condition to symplectic surfaces in two-dimensional complex space forms.

Let M be a complex two-dimensional Khler manifold with Khler form ω .Let Σ be a Riemann surface and we consider an isometric immersion f:Σ → M from Σ into M.Chern-Wolfson(cf.[6])defined the Khler angle θ of Σ in M by

where dμΣis the area element of Σ in the induced metric.It is said that Σ is a holomorphic curve if cosθ=1, Σ is a Lagrangian surface if cosθ=0 and Σ is a symplectic surface if cosθ＞ 0.

A symplectic minimal surface is a critical point of the area of surfaces,which is symplectic.Han-Li(cf.[7])considered generally the critical point of the functional

in the class of symplectic surfaces.The Euler-Lagrange equation of this functional is

where()⊤and()⊥mean tangential components and normal components of()respectively.Such a surface is called a symplectic critical surface.

Many interesting results about symplectic critical surfaces have been obtained by Han et al.(cf.[7–11]).In this paper we will focus on the explicit characterization of symplectic critical surfaces from the viewpoint of differential geometry.It follows from Eq.(1.3)that a minimal surface with constant Khler angle that values in[0,)is a symplectic critical surface.There are few examples of symplectic critical surfaces that is non-minimal.Han-Li-Sun(cf.[11])gave a two-parameters family of symplectic critical surfaces in two-dimensional complex plane,which is rotationally symmetric.Later,He-Li(cf.[12])showed the symplectic critical surfaces with parallel normalized mean curvature vector inmust be the above examples,and there does not exist any symplectic critical surface with parallel normalized mean curvature vector in two-dimensional complex space forms of non-zero constant holomorphic sectional curvature.So,it is natural to considering what kind of symplectic critical surface must be minimal.

In Sec.2,we introduce the concept of ellipse of curvature.In Sec.3,we study the fundamental equations of symplectic critical surfaces with circular ellipse of curvature in two-dimensional complex space forms by using the method of moving frame(cf.[6]).In Sec.4,we study the equations under the condition ρ=0 and get all solutions of the equations explicitly in this case.In Sec.5,we give a geometric result.Concretely,we prove that the symplectic critical surfaces with circular ellipse of curvature in two-dimensional complex space forms are minimal(cf.Theorem 5.1).

2 The Ellipse of Curvature

Suppose that M is a 4-dimensional Riemannian manifold.Let Σ be a Riemann surface and f:Σ→M be an isometric immersion.Letbe the mean curvature vector field of f.We denote the metric of M as well as the induced metric in Σ by＜,＞.If A:TΣ×TΣ → T⊥Σ is the second fundamental form of f,the ellipse of curvature is the subset of the normal plane defined as.To see that it is an ellipse,we consider an arbitary orthogonal tangent frame{v1,v2},denote hij=A(vi,vj),i,j=1,2,and look at the following formula for v=cosτv1+sinτv2:

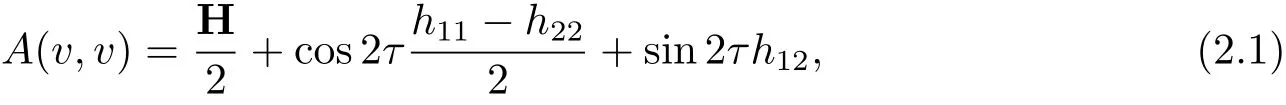
From Eq.(2.1),it is not difficult to deduce that the ellipse of curvature is a circle if and only if

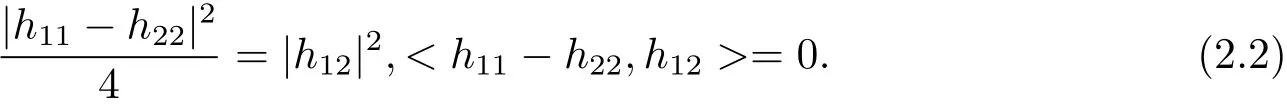
3 The Fundamental Equations of the Surfaces

Suppose that M is a complex two-dimensional Khler manifold of constant holomorphic sectional curvature 4ρ.Let{ωi}be a local field of unitary coframes on M,so that the Khler metric is represented by P.Here and in what follows,we will agree on the following range of indices:1≤ i,j,k ≤ 2.We denote by ωijthe unitary connection forms with respect to{ωi}.So we have

Let Σ be a Riemann surface and f:Σ → M be an isometric immersion.Letbe the mean curvature vector field of f.We assumehas no zeros on Σ.We can construct a unique system of global orthonormal vector fieldsalong Σ such thatandare tangent to Σ by the following:First we set the normal vector fieldof T⊥Σ arbitrarily,then the normal vector fieldof T⊥Σ is uniquely determined by choosing it to be compatible with the fixed orientations of Σ and M.The system of vectorsis linearly independent,because f is neither holomorphic nor anti-holomorphic.Here the angle of Jandis equal to the Khler angle θ which is defined in Sec.1.In fact,set

Moreover,we define vector fields e1and e3as follows:

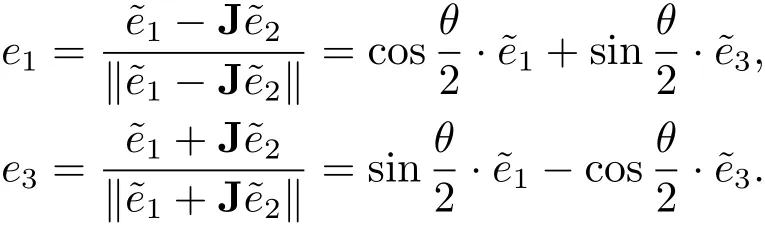
and put

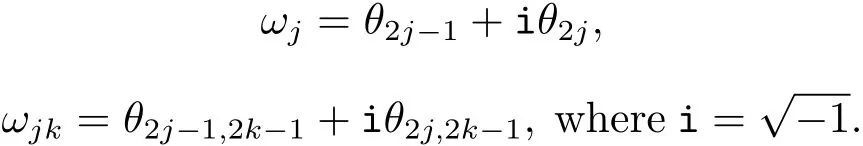
Then we have the following relations

and

We denote the restriction of{}to Σ by the same letters.Then we haveon Σ.Putting,the induced metric of Σ is written as ds2=.By taking the exterior derivative of Eq.(3.2)restricted to Σ,we get

where a,b and c are complex-valued smooth functions defined locally on Σ.Let{}be the components of the second fundamental form so that.By using Eqs.(3.3)and(3.4),all’s can be expressed in terms of a,b and c.Indeed,we have

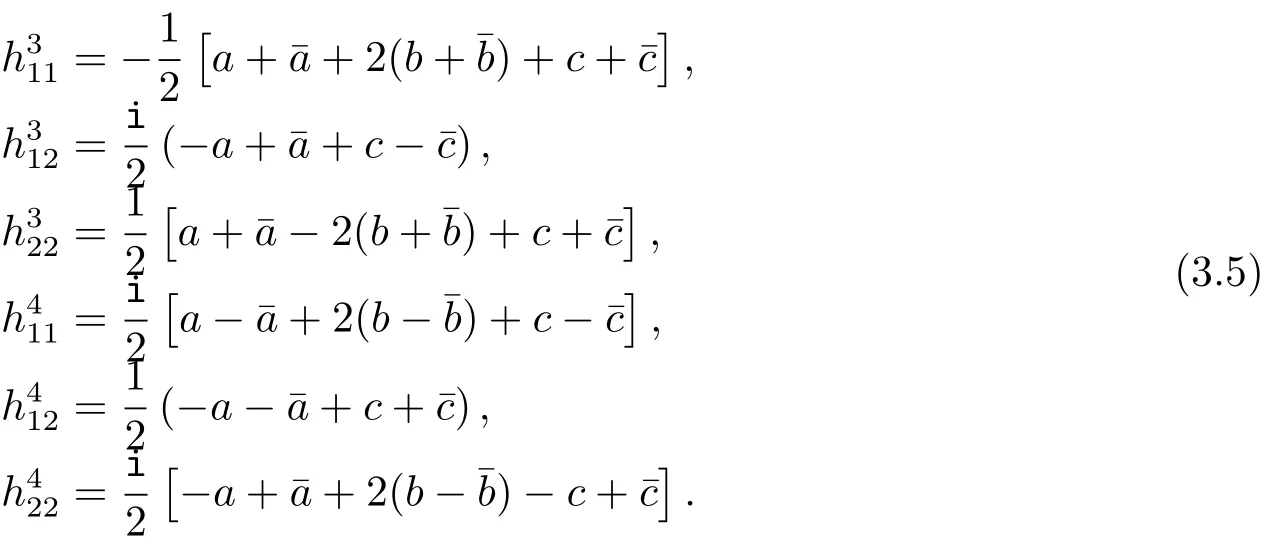
Let K be the Gauss curvature of Σ,then

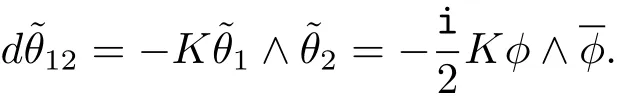
By taking the exterior derivative of the first formula of Eq.(3.3),using Eq.(3.1)and Eq.(3.4),we have

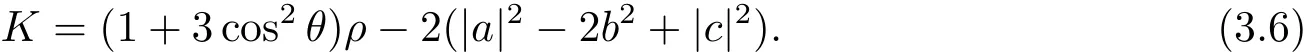
Since

then

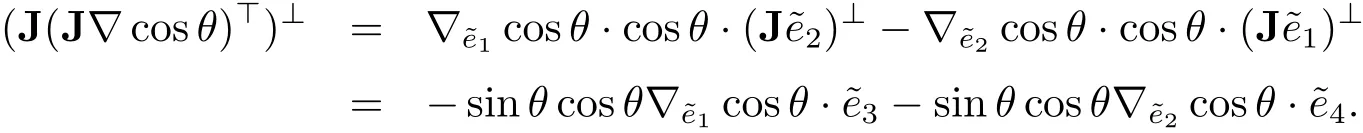
Hence,in particular,sinθ/=0.From the symplectic critical surface equation Eq.(1.3),we get

and

It follows from the first formula of Eq.(3.4)that

Combining Eqs.(3.9)and(3.10),we have

which implies

Substituting Eqs.(3.12)into(3.8),we obtain

Next,we study the fundamental equations of symplectic critical surfaces with circular ellipse of curvature.

Using Eq.(2.2),we can obtain From Eq.(3.5),using the above two equations,we can get a=0 or c=0 at any point p∈Σ.When a=0,using Eq.(3.13),we can know that b=0,so=0 at p,i.e.p is a minimal point.When c=0,we obtain the following proposition:

Proposition 3.1If Σ is a symplectic critical surface with circular ellipse of curvature in M,let U={p ∈ Σ|θ(p)/=0},then we have,on U,

ProofFrom the first formula of Eq.(3.4),we have

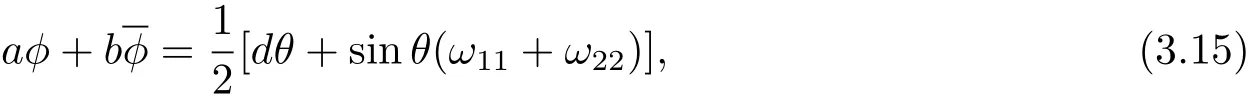
where a,b,θ are all real.Taking the exterior derivative of Eq.(3.15),we get

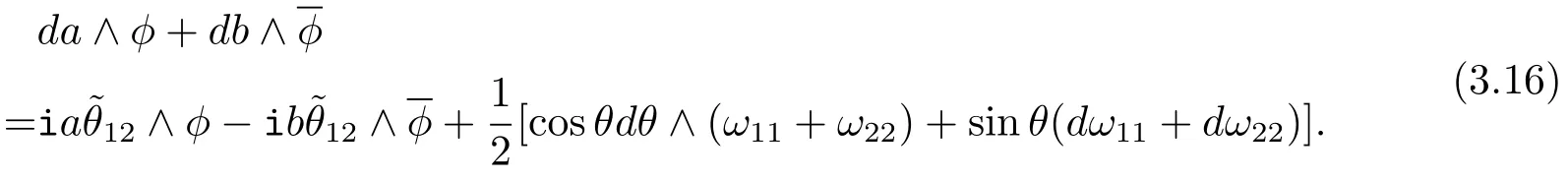
From Eq.(3.15),using

we get

which implies

which implies

Then using Eq.(3.1),we get

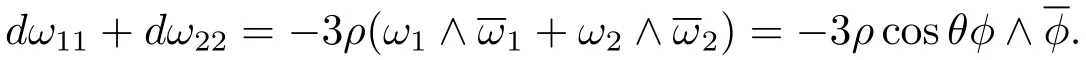
Hence,

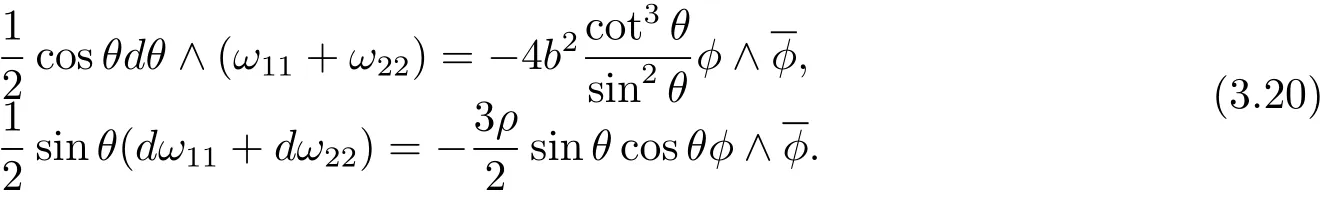
Using Eqs.(3.16),(3.17)and(3.20),we have

From the second formula of Eq.(3.4),we have

Taking the exterior derivative of Eq.(3.22),we get

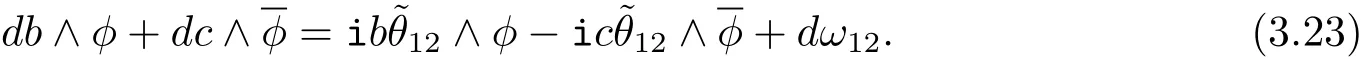
Since c=0,then we have

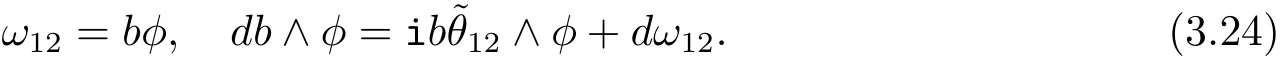
From the second formula of Eq.(3.1),we have

Using Eqs.(3.19)and(3.24),we get

By the conjugate of the above equation,we have

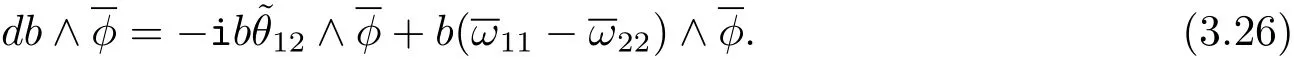
Combining Eqs.(3.21),(3.25)and(3.26),we have

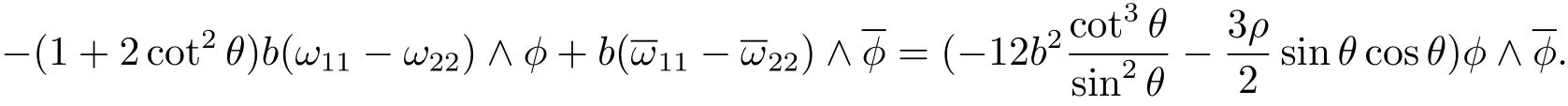
Taking the conjugate of the above equation,we have

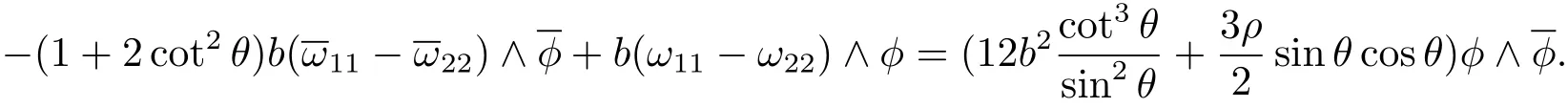
Using the above two equations,we get

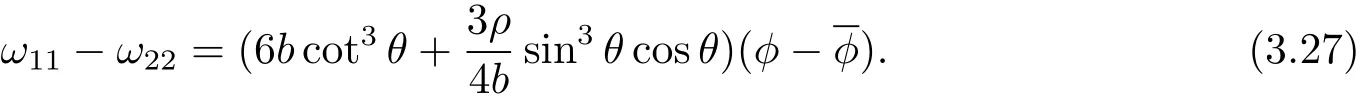
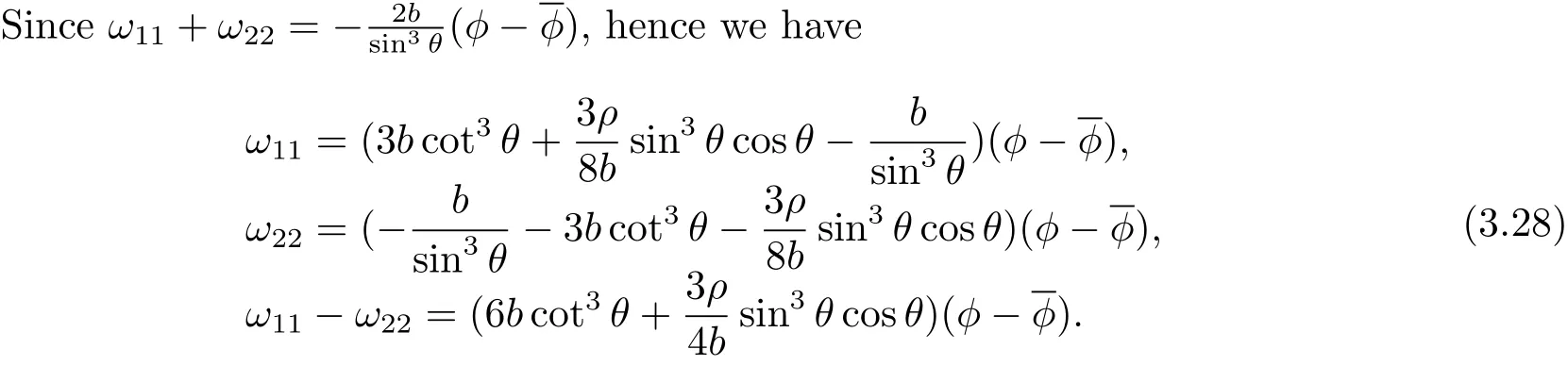
Using Eq.(3.3),we get the first formula of Eq.(3.14).Then using Eqs.(3.25)and(3.28),we have

then we get the third formula of Eq.(3.14).

Thus,we finish our proofs.

Remark 3.2Next,we discuss the case of U= Ø.In fact,if U= Ø,then θ≡ 0 on Σ,which implies Σ is a holomorphic curve in M.Of course it is a minimal surface.

Set φ = λdz,where λ is a non-zero complex-valued function on a simply connected domain U1⊂U with complex coordinate z.Then the set of the first three formulas of Eq.(3.14)is rewritten as the following system of differential equations:

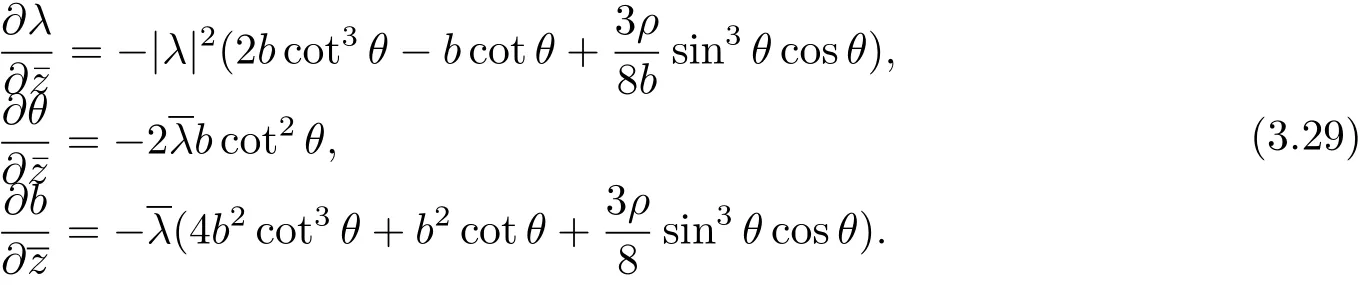
In the following we give a lemma about the existence of isothermal coordinate.

Lemma 3.3Suppose Σ is a symplectic critical surface with circular ellipse of curvature in M.Then there exists a complex coordinate w on a neighborhood of a point of U⊂Σ such that φ = μdw,where μ is real-valued.

ProofSince θ is not constant,we claim that b is a function of θ.In fact,canceling out(φ+)in the second and third formula of Eq.(3.14),we get a differential equation in b for θ.Using the claim,we write b=b(θ),and define a real-valued function

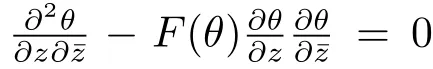
the lemma is proved by the conjugate of the second formula of Eq.(3.29).

Hence,for a neighbourhood U of a point of Σ,there exists an isothermal coordinate z=u+iv such that

where λ is a positive function defined on U,and we have

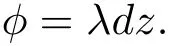
This implies that λ,θ and b are functions of single variable,and Eq.(3.29)is seen to be a system of ordinary differential equations.Consequently,if Σ is a symplectic critical surface with circular ellipse of curvature in M,then there exist real-valued smooth functions of single variable λ,θ and b which are defined locally on Σ and satisfy the system of ordinary differential equations(cf.Eq.(3.30)).

Theorem 3.4Let M be a two-dimensional complex space form of constant holomorphic sectional curvature 4ρ.If Σ is a symplectic critical surface with circular ellipse of curvature in M,then there exist a system of local coordinates(u,v)on Σ and real-valued smooth functions λ(u),θ(u)and b(u)of single variable u which are defined on an interval I of u,such that they satisfy a system of ordinary differential equations

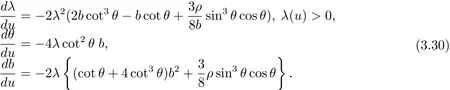
4 Analysis of the Overdetermined System:ρ=0 Case

When ρ=0,we get all solutions of the system Eq.(3.30)as follows.

Lemma 4.1Assume that ρ=0.Then all solutions of the system Eq.(3.30)are given by

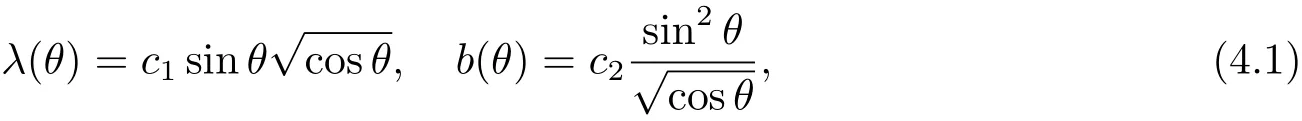
for any positive constants c1and c2.

ProofSince both θ(u)and b(u)are not constants,regarding θ as variable,we get from Eq.(3.30)that

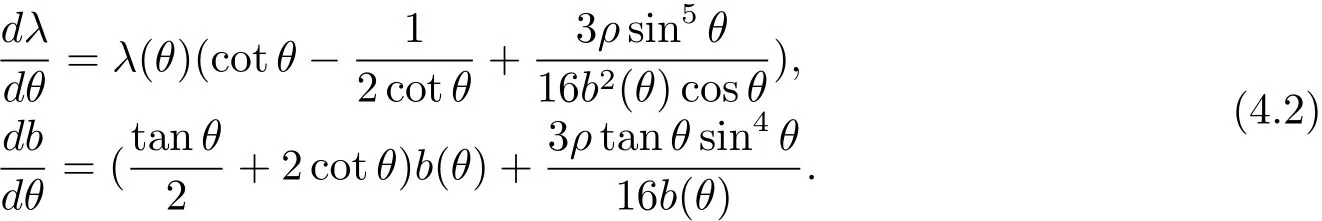
Since ρ=0,the equations above reduce to

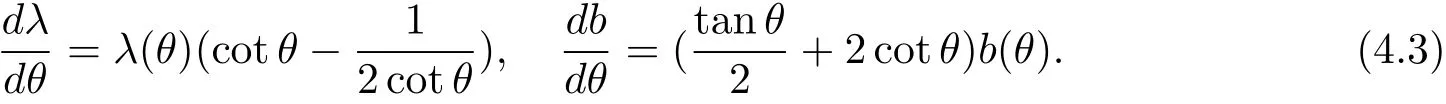
The integration of the above equations give us the solution of λ(θ)and b(θ)as follows:

for any positive constants c1and c2.Hence we finish our proof.

5 The Geometric Result

In this section,we show a geometric result.

Theorem 5.1Let M be a two-dimensional complex space form of constant holomorphic sectional curvature 4ρ.If Σ is a symplectic critical surface with circular ellipse of curvature in M,then Σ is a minimal surface in M.

ProofFirst,we prove our result in the case of ρ/=0:

We already know that

and that

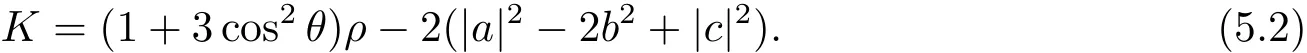
Using the first equation of Eq.(3.30)and Eq.(5.1),we can get

Using Eqs.(3.13)and(5.2),since c=0,we have

Combining Eqs.(5.3)and(5.4),we get

Regarding θ as variable,taking the derivative of Eq.(5.5)and using the second equation of Eq.(4.2),we have

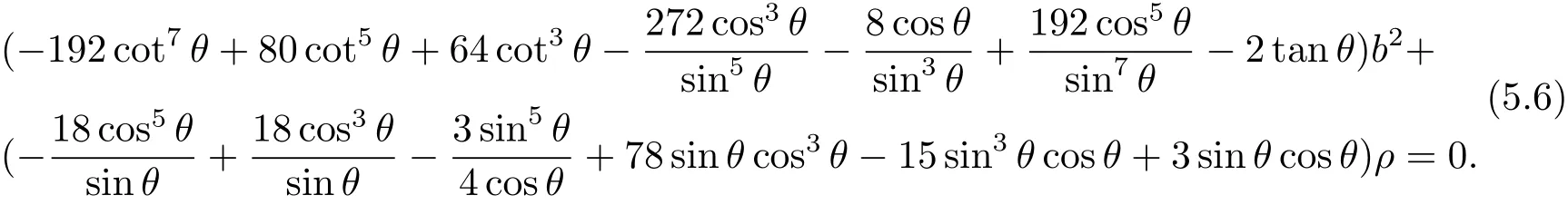
Set x=sinθ.Using Eq.(5.5),we have

Taking Eq.(5.7)into Eq.(5.6),we get

Hence,x is constant,then θ is constant.So b=0 by the second formula of Eq.(3.30),i.e.=0.Thus,we finish the first part of our proofs.

Now,we prove our result in the case of ρ=0:

When ρ=0,using the second formula of Eq.(4.1)and Eq.(5.3),we have

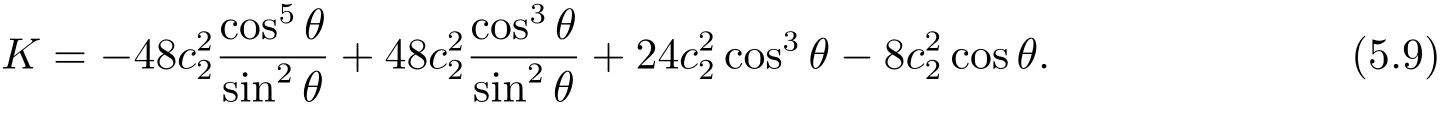
Using the second formula of Eq.(4.1)and Eq.(5.4),we get

Combining Eq.(5.9)and Eq.(5.10),we can have

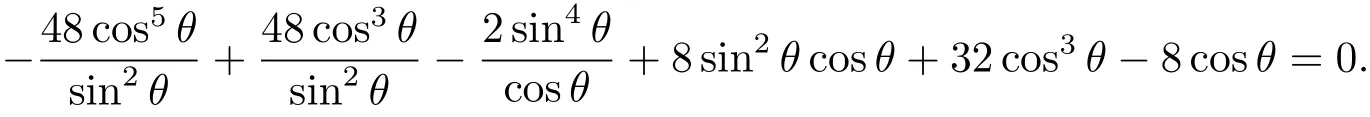
Set x=sinθ,then we get

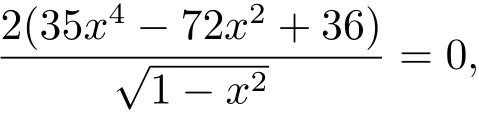
hence x is constant,then θ is constant.So b=0 by the second formula of Eq.(3.30),i.e.=0.We finish our proofs.

Remark 5.2The coordinate of b2in Eq.(5.5)doesn’t equal to 0.Setting x=sinθ,from the calculation by Mathematica,we can know that

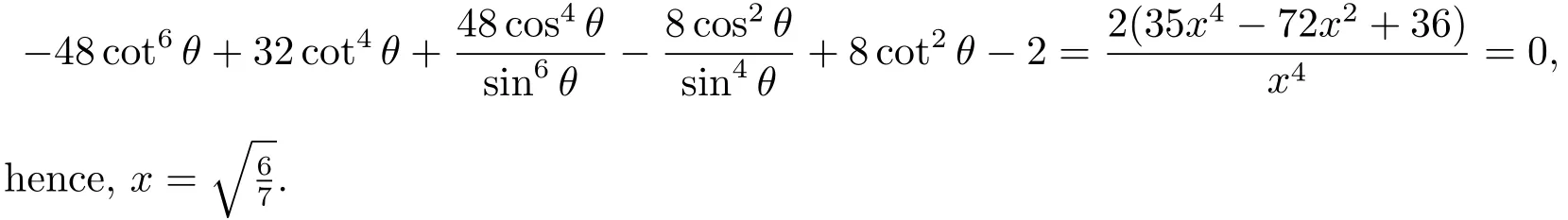
and solve the equation by Mathematica,but we can’t have the solution in(0,1).It’s a contradiction.So the coordinate of b2in Eq.(5.5)doesn’t equal to 0.

Remark 5.3From the discussion in Remark 5.2,we can know that the denominator in Eq.(5.8)doesn’t equal to 0.

As we already know that any closed symplectic minimal surface in a Khler-Einstein surface with non-negative scalar curvature is holomorphic,we have the following Liouville theorem:

Corollary 5.4Any closed symplectic critical surfaces with circular ellipse of curvature in two-dimensional complex space forms with non-negative holomorphic sectional curvature must be holomorphic.

AcknowledgmentsThe authors would like to appreciate Professor Jun Sun for some helpful discussions about symplectic critical surfaces and the excellent suggestion of writing a Liouville theorem as a corollary of the main result.