THE SPREADING SPEED FOR A NONLOCAL DIFFUSIVE PREDATOR-PREY MODEL WITH ONE PREDATOR AND TWO PREYS
2022-02-11BIWenlianZHOUWen
BI Wen-lian,ZHOU Wen
(School of Mathematics and Statistics,Anhui Normal University,Wuhu 241002,China)
Abstract:In this paper,we investigate a nonlocal diffusive predator-prey model with one predator and two preys.Our main concern is the invasion process of the predator into the habitat of two aboriginal preys.By using comparison principle and semigroup theory of reaction diffusion equation,we con firm the asymptotic spreading speed of the predator.
Keywords:predator-prey system;spreading speed;nonlocal diffusion;comparison principle;Invasion
1 Introduction
In recent years,the reaction-diffusion equation with nonlocal diffusion effect has gradually become a hot research area in the field of materials science and biological mathematics[1–3].The introduction of nonlocal diffusion terms in mathematical modeling can,in many cases,better describe some natural phenomena.Although many scholars[4,5]have studied the traveling wave solutions of reaction-diffusion equations with nonlocal diffusion effect,there is little research on invading phenomenon in reaction-diffusion systems.
Recently,Ducrot et.al[6]have investigated a two-species predator-prey model with nonlocal dispersal as follows
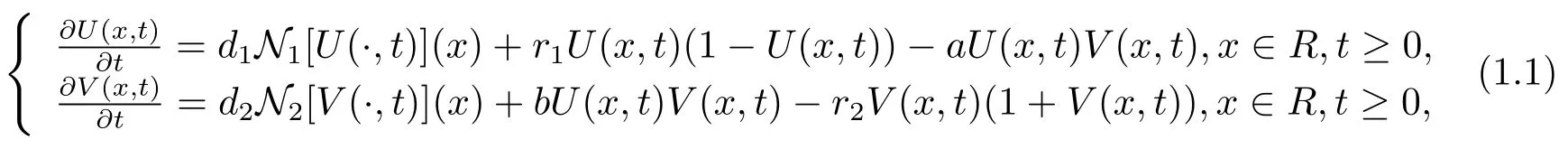
in which the terms d1and d2describe the spatial dispersal of the prey and the predator,other coefficients are nonnegative constants.is the linear nonlocal diffusion operator defined by

wherein Ji,i=1,2 are probability kernel functions and the symbol*denotes the concolution product relative to the space variable,x∈R(We also refer readers to specific definitions by[7]while be given later).Under certain conditions,they obtained the spreading speed c1of predator invading native prey habitat as follow
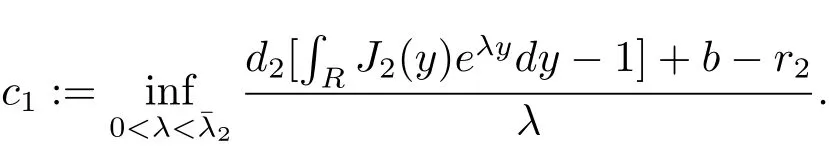
In fact,due to the diversity and complexity of ecosystems,it is more practical to study the interaction between multiple species.However,when there are more than two species,it becomes more difficult to study the ecosystem.Chin-Chin Wu[8]has studied the following three-component reaction diffusion system

where di,ri,ai,bi,i=1,2,3 are positive constants.When the above system satisfies a series of conditions such as a1,a2<1 and b1=b2=b>1,the author has characterized the asymptotic spreading speed c2of the predator with

Remark 1.1In the system(1.2),the author assumes that the predator has the same predation rate to the two kinds of preys and it is also the conversion rate of the predator’s absorption.These hypothetical conditions make the predator-prey model too idealistic.Moreover,the author does not consider the spatial nonlocal diffusion.For the system(1.1),the authors consider the spatial nonlocal diffusion effect,but the model only has two species.So it is reasonable for us to consider the model of three species interaction.To the author’s knowledge,the asymptotic spreading speed of three species model with nonlocal diffusion effect is still a problem to be solved.
In this paper,we consider the following three-component reaction-diffusion system with nonlocal dispersal
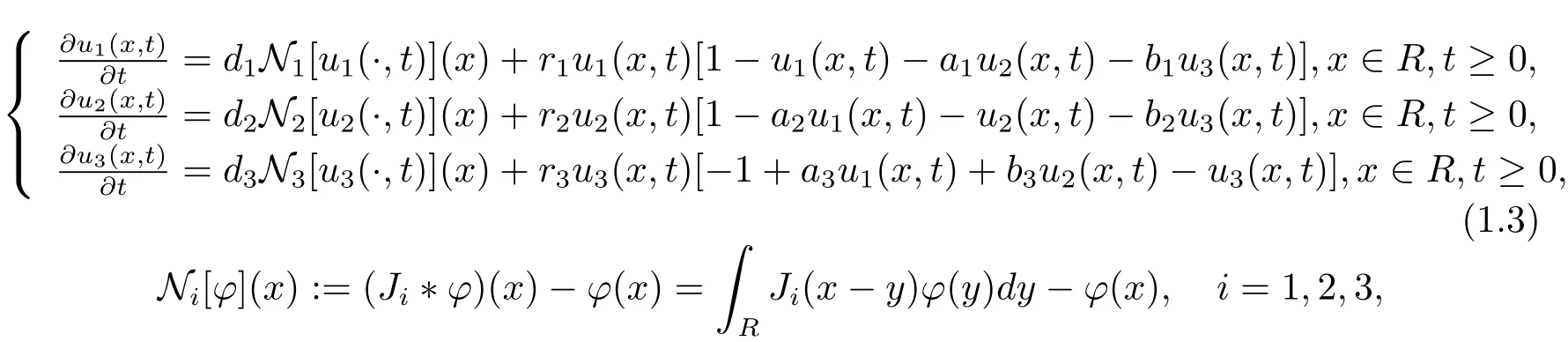
where di,ri,ai,bi,i=1,2,3 are positive constants,u1,u2and u3represent the population density of preys and predator at space x and time t,respectively.The parameters r1and r2represent the growth rates of u1and u2,r3is the death rate of u3,a1and a2represent the interspecific competition coefficient of two kinds of preys,r1b1and r2b2are the predation rates,and r3a3,r3b3are the conversion rates.
It’s noting that system(1.3)represents a model of a three-species system in which two preys compete with each other and are preyed upon by a predator.Such systems occur frequently in nature.For example,one population could be the predator such as lady beetles,and the second and third could be prey species such as English grain aphid and the oat-bird cherry aphid[9].
In this paper we study a three-species predator-prey model with nonlocal diffusion.Our main concern is the invasion process of the predator into the habitat of two aborigine preys.Under certain conditions,we are able to characterize the asymptotic spreading speed by the use of comparison principle and semigroup theory.Moverover,we can get the same results as system(1.2)by degenerating our system.
2 The Spreading Speed of the Predator
For the sake of describing the process of species invasion,we need to introduce some measures such as the asymptotic spreading speed.
Definition 2.1[10]Let z(x,t)be nonnegative for x∈R,t>0.Then s*is called the spreading speed of z(x,t)when

In this paper,we assume that Ji,i=1,2,3 satisfies the following definition.
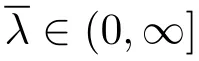
(J1)The kernel J is nonnegative and continuous in R;
(J2)For all x∈R it holds that

(J3)it holds that RRJ(y)eλydy < ∞ for any λ ∈ (0,)and


where N[w]=:J*w-w and 0<z(x)≤s is a bounded and continuous function with nonempty support,for the scalar nonlocal equation enjoys the following comparison principle.
Lemma 2.1[12]Let z(x,t)be a solution of(2.1),z(·,t),t> 0 and 0 < z(x)≤ s are continuous and bounded for x∈R,t>0.Assume that 0<w(x,0)≤s and w(x,t)are continuous and bounded for x∈R,t>0,if they satisfy
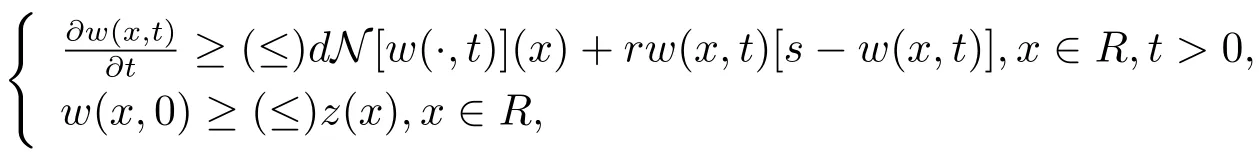
then w(x,t)≥(≤)z(x,t),x∈ R,t>0.
Lemma 2.2[12]Let z(x,t)be a solution of(2.1),z(·,t)is continuous and bounded for all t>0 for a given 0<z(x)≤s.If z(x)has a nonempty compact support.Then we have
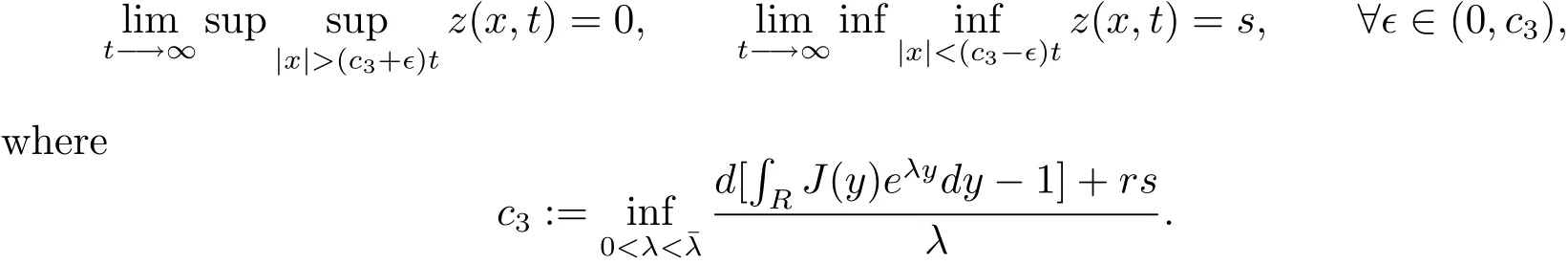
In this paper,due to the weak competition between two preys,we consider the following initial conditions of the system(1.3)
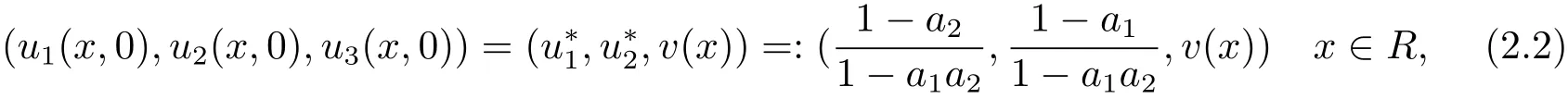

Because of the nonnegativity of u1,u2and u3,we can easily get u1(x,t)≤1,u2(x,t)≤1 for all(x,t)∈R×[0,∞)by the comparison principle.Hence u3(x,t)satisfies the equation
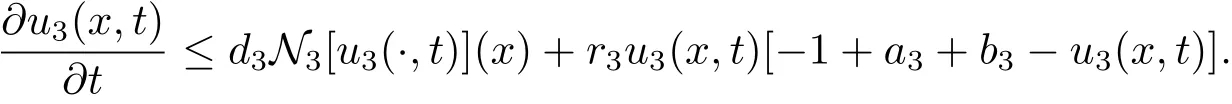
By Lemma 2.1,we have u3(x,t)≤-1+a3+b3.
Further by a comparison,we obtain

Since the asymptotic spreading involves long time behavior,we have

Next,we discuss the spreading speed of the predator u3(x,t)in system(1.3)with following conditions
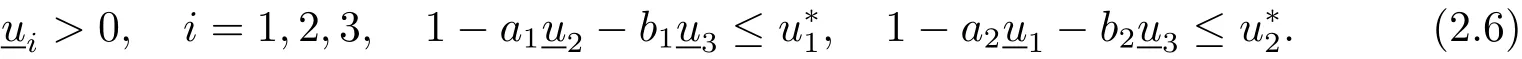
We now state our main result on the spreading speed of the predator as follows.


Theorem 2.1Assume that conditions of(2.6)are enforced.Let(u1(x,t),u2(x,t),u3(x,t)),x∈R,t>0 be a solution of(1.3)with initial data(2.2).As long as v(x)is a non-zero compactly supported continuous function with 0≤ v(x)≤ α,then the density of the predator u3(x,t)satisfies
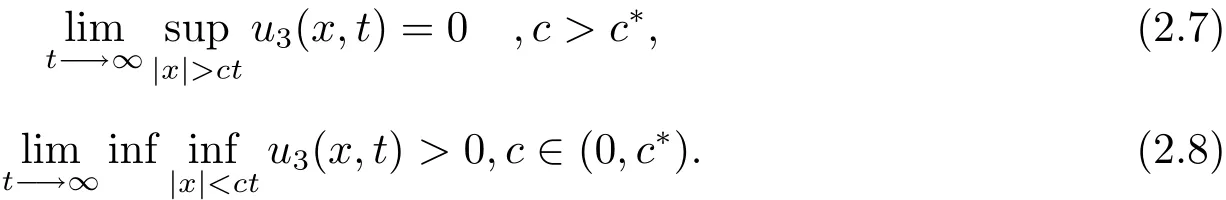
Now we first prove(2.7).On the base of the results of(2.3)-(2.6),we have

Further,u3(x,t)satisfies
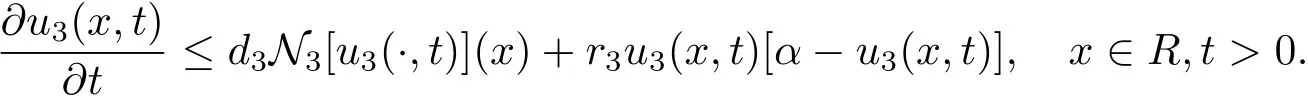
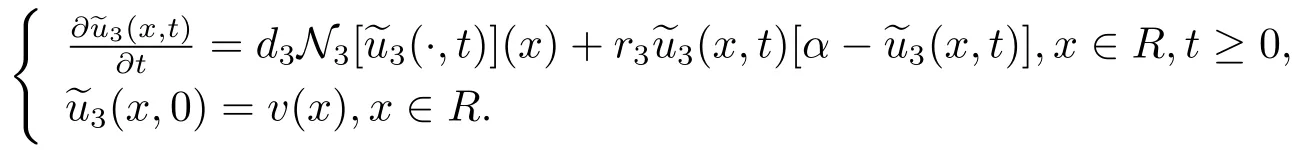
It follows from the classical result of Lemma 2.2 that


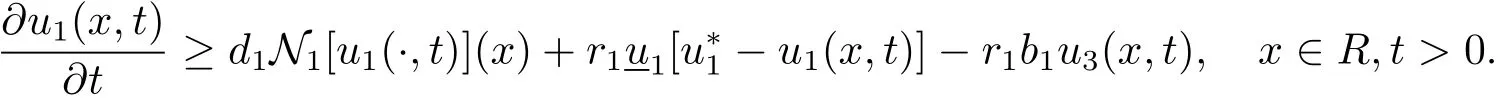
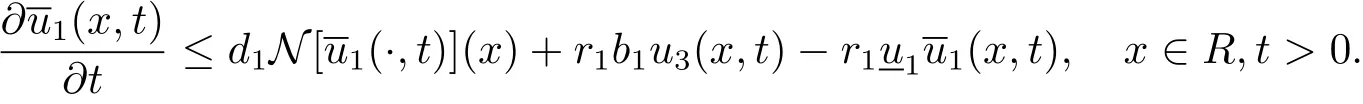


It follows from the third formula of system(1.3)that

For any given constant∈∈ (0,c*),we can choose constant δ∈ (0,α)small enough such that
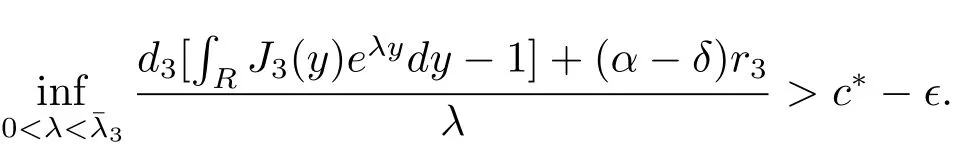
We first assume that there exist M1> 0,M2> 0 and τ1> 0,τ2> 0 large enough such that
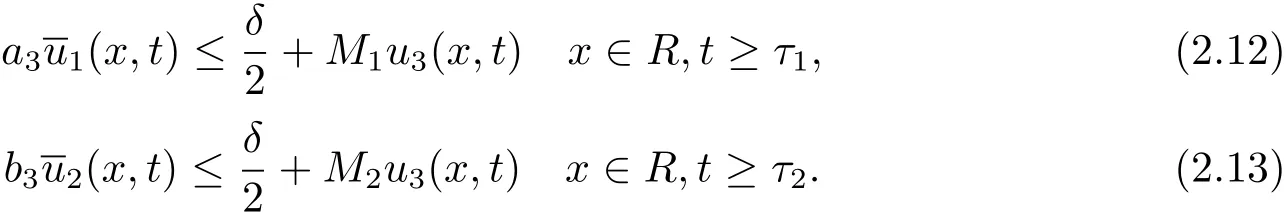
Then,combining(2.12),(2.13)with the third formula,we obtain
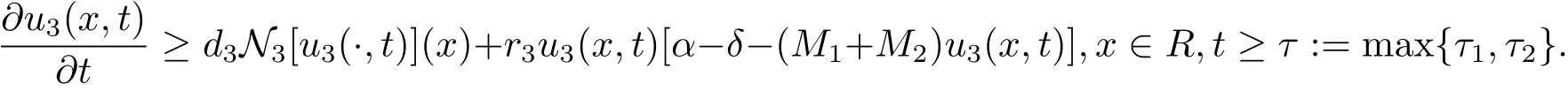
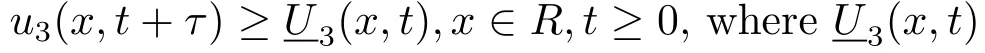
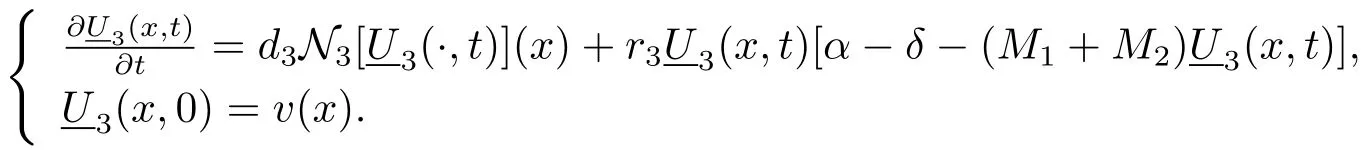
Finally,combining Lemma 2.2 and Lemma 2.3,we obtain

Hence,this completes the proof of(2.8)since∈is arbitrary.
To complete the proof of Theorem 1.1,it remains to derive(2.12)and(2.13).In the following,we only prove the formula(2.12).In order to achieve our goal,we need to know more detailed properties about the strongly positive semigroup Ti(t):=exp(tdiNi).
Let Z(x,t)be a solution of the following problem

wherein δ0(x)denotes the Dirac mass at x=0.According to[12],Z(x,t)can be decomposed into the following forms

where K(x,t)is a nonnegative smooth function andRK(x,t)dx≤2,t≥0.
For any bounded and continuous function 0≤ φ(x),the semigroup Ti(t),t≥ 0 can be expressed as
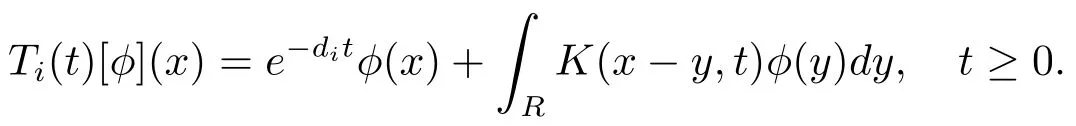
Next we start to prove the formula of(2.12).By(2.9),we have


For the fixed positive constant δ,there is a large enough constant τ1such that

In the circumstances,we deduce from(2.14)-(2.16)that

Further
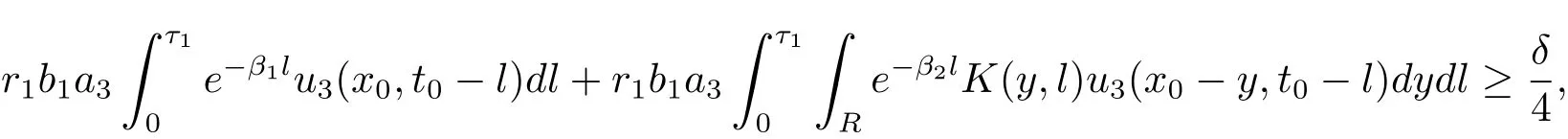
where l=t0-s.Next,we choose R>0 such that
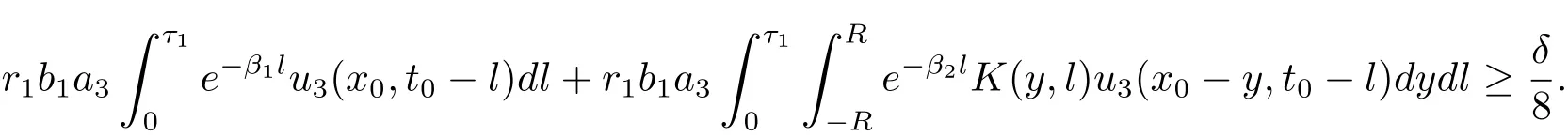
Note that R is independent of(x0,t0).Then we choose η > 0 small enough such that
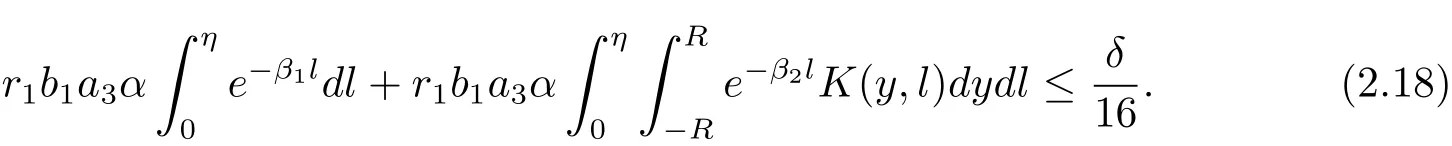
It follows from(2.17)that
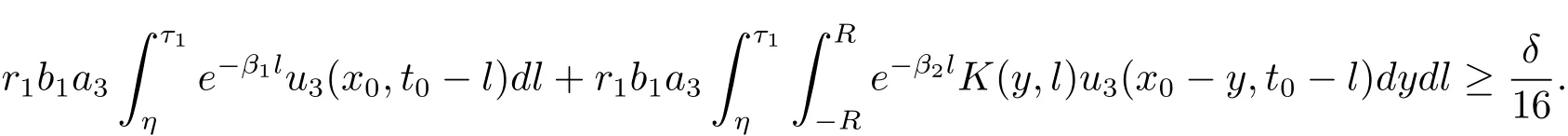
Then choose θ > 0 such that
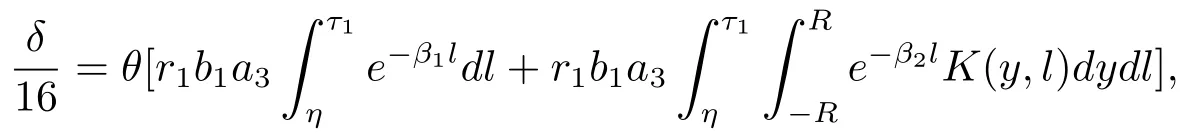
there exist l0∈ [t0-τ1,t0-η]and y0∈ [x0-R,x0+R]such that u3(y0,l0)≥ θ.Moreover,since the function u3(x,t)is uniformly continuous on R × [0,∞),there exists ρ > 0 independent of(y0,l0)such that u3(y,l0)≥,∀y ∈ [y0-ρ,y0+ρ].
We then consider the solution w(x,t)to

where w(x)is a uniformly continuous function with w(x)≤such that
(ii)w(x)=0, |x|≥ ρ;
By the comparison principle,we have w(x,t)≤u3(y0+x,l0+t),x∈R,t≥0.
Moreover,set w(x,t)=er3(1+α)texp(d3tN3)[w](x),we have w(x,t)> 0,x ∈ R,t≥ 0.Thus one obtains that

Further then it follows from(2.18)and(2.19)that

3 Example


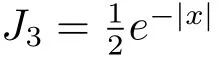
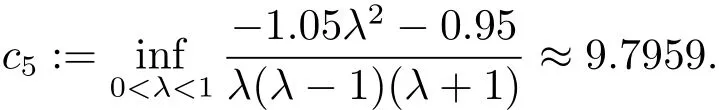

杂志排行
数学杂志的其它文章
- RESEARCH ANNOUNCEMENTS ON“MODERATE DEVIATIONS FOR GRENANDER ESTIMATOR NEARBOUNDARIES OF THE SUPPORT”
- ON REFINED YOUNG’S REVERSE INEQUALITIES FOR POSITIVE LINEAR OPERATORS
- SYMPLECTIC CRITICAL SURFACES WITH CIRCULAR ELLIPSE OF CURVATURE IN TWO-DIMENSIONAL COMPLEX SPACE FORMS
- STUDY ON 2-DIMENSIONAL SUBMANIFOLDS WITH CONSTANT DETERMINANT OF BLASCHKE TENSOR
- ON SPLIT REGULAR BIHOM-LIE COLOR ALGEBRAS
- RESEARCH ANNOUNCEMENTS ON“UPPER BOUND ESTIMATES OF EIGENVALUES FOR HRMANDER OPERATORS ON NON-EQUIREGULAR SUB-RIEMANNIAN MANIFOLDS”
