钻井水射流附壁振荡短节的频率和压降分析
2022-02-11何智恒李美求王冰冰
何智恒,李美求,李 宁,王冰冰
(长江大学 机械结构强度与振动研究所,湖北 荆州 434023)
水力振荡器作为大位移井钻进过程中降低摩擦阻力、提高钻井效率的有效手段,国内外[1-2]学者提出了各种各样的新技术。水力振荡器可以有效改善钻压,并变静摩擦为动摩擦,降低工具串与井壁的摩擦力,提高钻井效率。射流式水力振荡器利用附壁原理Conda效应产生射流振荡,控制活塞杆完成周期轴向运动。
众多学者对水力振荡器的振动特性及应用效果进行了大量研究[3-4]。吴志勇等[5]研究得出激振力以及安装位置对减阻效果的影响比较显著,而振动频率则影响较小。李斌等[6]则研究得到振动强度、振动频率、振幅对水力振荡器减阻效果的影响依次减小,并提出当振动频率为22 Hz时可以得到最佳减阻效率。柳鹤[7]等针对井下钻具强度,证明了水力振荡器的振动频率对井底钻具强度的影响为良性。赵钰和余长柏等[8-9]则分别针对振荡器的动定阀选型的配合对其阀口的频率和压降提供了设计参数参考。综上,目前对于水力振荡器的研究大多是针对其工作特性的分析。相较于传统轴向振动器,射流式水力振荡器具有结构简单、无需撞击元件、压降更低等优点,因而很多学者对其研究[10]。国内外对射流振荡器的研究主要是针对小口径小流量结构分析,应用范围包括:洒水灌溉、淋浴、散热等领域[11-12]。
本论文以射流附壁水力振荡器的振荡短节为研究对象,采用CFD数值模拟方法及单因素分析法,研究侧壁角度、侧壁高度、劈尖距离和反馈角度对振荡频率和压降的影响,得到不同结构参数对压降和频率的影响规律。本研究成果对射流式水力振荡器的优化设计和特性分析具有理论和工程指导意义。
1 射流振荡理论分析
1.1 射流附壁原理
流体经喷嘴口形成一股高速水射流。由于射流的高速运动,导致射流中心位置的流速快,在靠近两侧壁处的流速小。在速度差的作用下,逐渐在上下侧壁之间形成低压漩涡,导致流体不断靠近侧壁运动,在卷吸的作用下,射流最终附着在一侧壁流动,如图1所示。为了完成射流附壁的切换,在射流口出口上下分别设计反馈流道,当射流附着在一侧壁流动时,其对应一侧的反馈流道压力激增,不断冲击射流口流体,使其改变运动方向,推动流体逐渐向另一侧壁运动,如图2所示。在这种反馈作用下,流体不断进行附壁切换,最终高频的附壁切换就形成了射流振荡。

图1 射流附壁
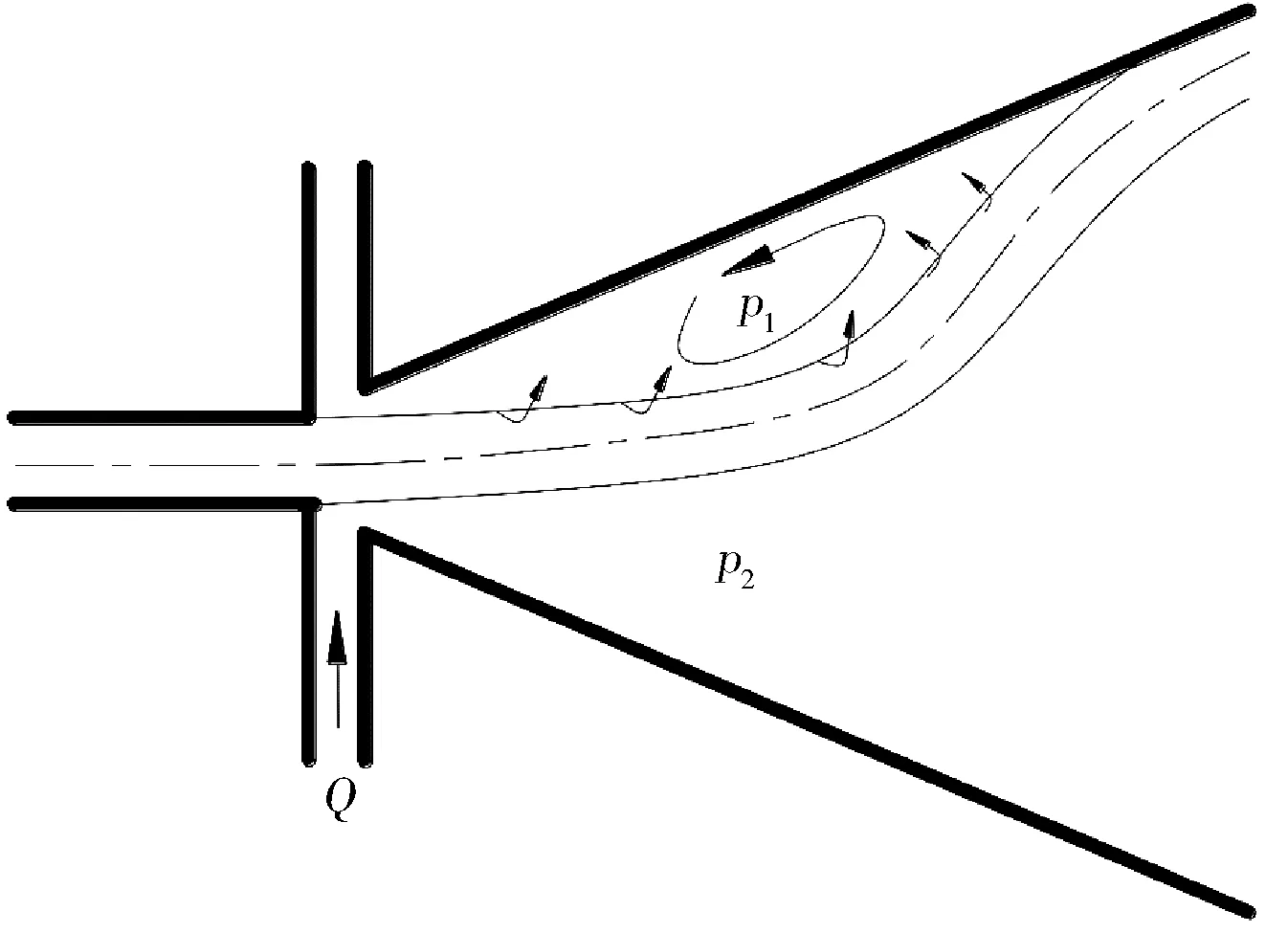
图2 射流附壁的切换
1.2 射流振荡分析
射流附壁参数如图3所示,流体经喷嘴口形成高速水射流,径直冲击劈尖,随后在卷吸的作用下实现射流向一侧壁的偏转附壁[13]。其中,射流口的直径为d,流体的速度v、密度为ρ,劈尖距离为l,侧壁角度为θ,射流的偏转角度为β。
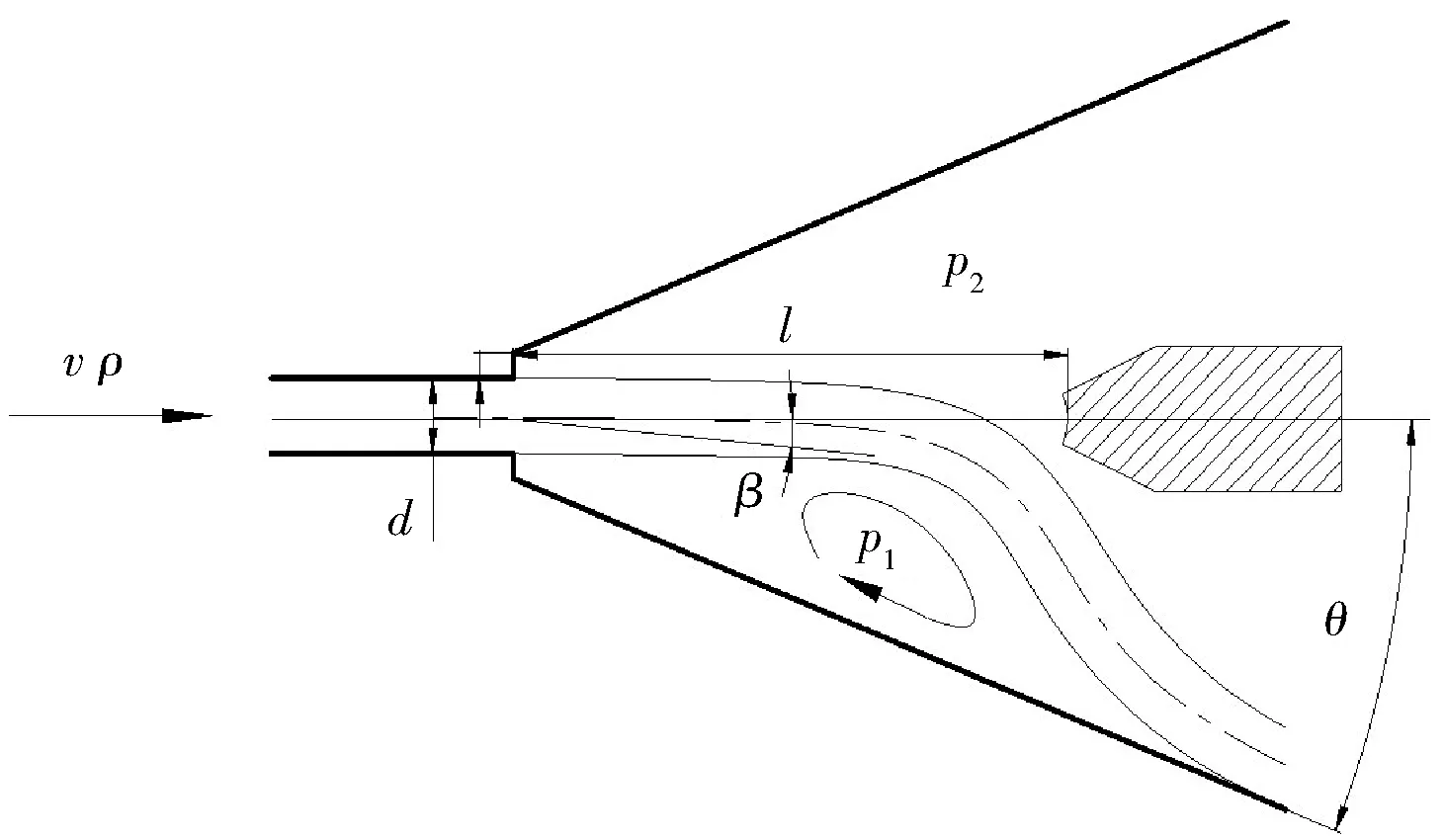
图3 射流附壁参数
在射流附壁过程中,假设为理想流体并忽略热量损失,根据动量守恒定理可以得到:
ρv2d=J+J1
(1)
(2)
式中:J为主射流的惯量;J1为射流靠近侧壁表面卷吸惯量;r为射流中某一微元的偏转半径;V为射流中流体的某一微元体积。
射流偏转角的计算公式[14]:
(3)
在卷吸作用下射流形成压力差,推动射流贴附在一侧壁,射流偏转半径的计算公式为:
(4)
式中:p1,p2分别为射流上、下侧压力;y为射流截面宽度。
根据式(1)和式(3),流体依靠卷吸作用发生偏转。当侧壁角度在0<θ<22.5°逐渐增加时,射流的偏转角有增大的趋势,此时射流较容易附壁。当侧壁角度在22.5°<θ<45°逐渐增大时,射流偏转角有减小的趋势,此时射流很难附壁。再根据式(4)射流的偏转半径随着射流附壁过程逐渐的增大,说明射流附壁的位置受到流量的影响。
在射流附壁的主动控制过程中,反馈流体不断提高射流与附壁侧的压力,射流附壁位置沿着侧壁向后运动,最后在劈尖的作用下完成向另一侧壁的附壁,劈尖和射流口的间距大小会影响水力振荡频率。侧壁的距离h对射流振荡也有影响,当h过大时,则需要有足够大的偏转角度才能使射流附壁。
根据流道结构自激发引起射流振荡的形式有多种[10],控制流是决定射流振荡的重要因素。当控制流与主射流呈夹角时,控制流有推动主射流附壁切换的效果,当控制流平行于主射流时,控制流有促进射流附壁的效果[15]。
2 射流振荡动力计算
2.1 水力振荡器的特征参数
本文以低压降为目标设计大直径射流式水力振荡器,主要研究射流脉冲短节的各个关键结构参数变化分别对于水力振荡特性的影响。根据国内外对于射流脉冲结构的研究[16-18],影响射流元件振荡特性的主要因素有:射流口与附壁高度宽度比值,一般取0.2∶1~0.6∶1;射流口与侧壁的夹角,取10~30°;射流口与劈尖距离和宽度比值,取1∶3~1∶12。此外,由于他人研究中的射流脉冲形式不尽相同,例如音波式、共鸣式及反馈式的控制流道可能有不同结构,本文将反馈流道角度的影响因素也加入研究,对4种结构参数进行单因素敏感性分析。
为了便于直观地展示各结构参数,对分析的结构参数样式进行了简化和标注,射流元件的结构平面简图如图4所示。射流口的宽度为d,侧壁相对于射流口高度为h,反馈流道与射流口的夹角为a,射流口到劈尖之间距离为l,凹劈尖的半径为R,斜侧壁和射流口所呈夹角为θ。
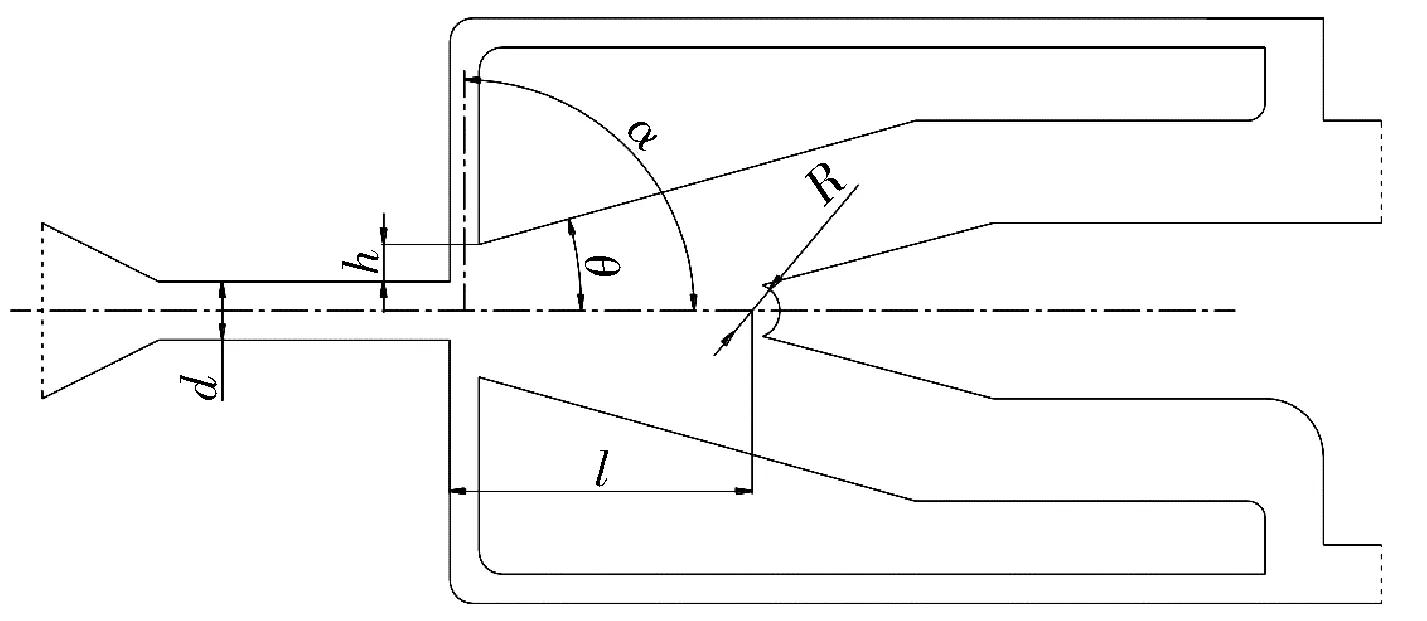
图4 射流元件简图
本文分析在流量20 L/s的工作环境下,水力振荡短节的侧壁角度、侧壁高度、劈尖距离、反馈角度对射流式水力振荡短节频率及压力的影响规律。依据国内外对水力振荡短节结构的研究选取参数如表1所示。
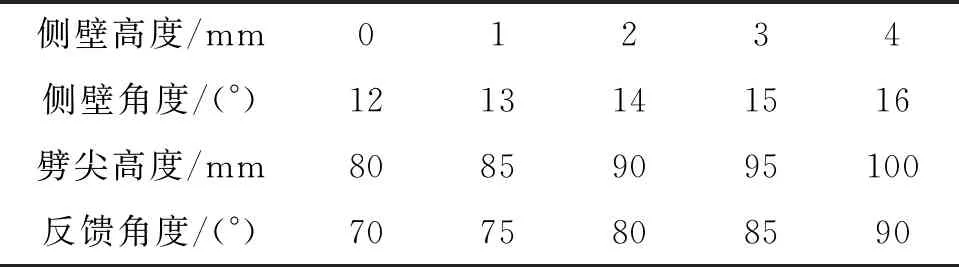
表1 主要结构参数
2.2 水力振荡器的流体计算
使用Solidworks进行三维建模,提取水力振荡器的流体域并对流体域进行计算,然后导入STAR-CCM+软件进行流体瞬态动力学计算。采用Trimmed网格进行划分,保证大部分为结构网格[19],对整体模型划分棱柱层网格,网格尺寸为,棱柱层厚度相对尺寸为,在射流口与反馈流道相贯处、劈尖处、缸体上腔与射流上腔、缸体下腔与射流下腔进行网格细化。单元总数为204 972个,计算域的网格如图5所示。
在瞬态计算中,参考国内外对相似结构分析时选取的分析方法和参数选择,对射流口流量设置为20 L/s,节流盘尾部出口边界条件设置为0,壁面处选择粘性流体无滑移条件,近壁面采用标准壁面函数。瞬态计算总时间t=0.2 s,时间步为0.001 s,流体介质为水,选择湍流RNGk-ε模型。分别选取水力振荡短节的入口、缸体上腔、缸体下腔、节流口处进行数据的提取,如图6所示。
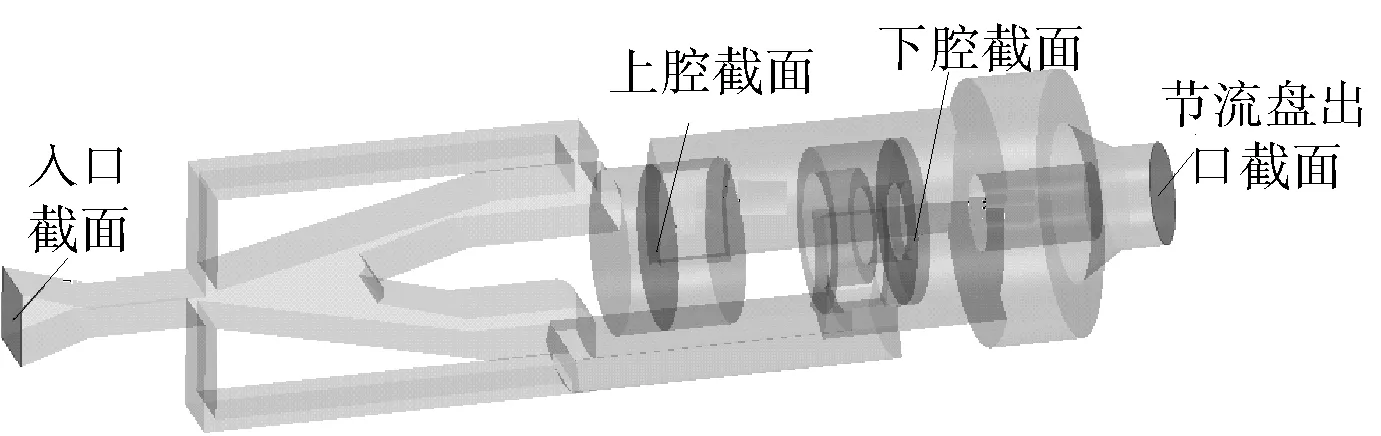
图6 数据提取端面
通过建立几何模型、选择湍流模型、建立网格模型、设置边界条件、时间步以及模拟参数等操作,就可以对射流式水力振荡器流体域进行瞬态模拟计算。
通过瞬态模拟计算,对射流脉冲的初始状态进行分析,可以得到流速分布云图,并直观地观察到流体在水力振荡器中的分布规律。射流水力振荡器从开始工作至第1次附壁切换,流体的分布情况如图7所示。

图7 流速分布云图
由图7可以看出:
1) 0.01 s时,流体经过射流口喷出加速,并径直冲向劈尖,流体向上下流道相对均匀流动,而在反馈流道中几乎没有流体运动,节流口开始有流体汇入。
2) 0.02 s时,射流逐渐向右侧壁附壁,右侧反馈流道中流体运动明显,并开始冲击射流口,活塞上腔中流体运动剧烈,节流口大范围出现流体运动。
3) 0.07 s时,射流在右侧反馈流道流体作用下开始向左侧壁倾斜,但仍然附壁于右侧壁,同时活塞上腔区域扩大,右侧反馈流道流体流速减缓。
4) 0.08 s时,射流开始附着于左侧壁,活塞下腔通道和左侧反馈流道流体运动渐涨,活塞上腔中的流体由于泄流口开度增大,向低压的泄流口流动,表现出活塞上腔流速增大的迹象。此时水力振荡器的第1次附壁切换结束。
2.3 计算结果
采用单因素敏感性分析法,使用表1的自变量取值,最终得到20组数据。列举侧壁高度单因素影响的分析计算结果,如图8所示。
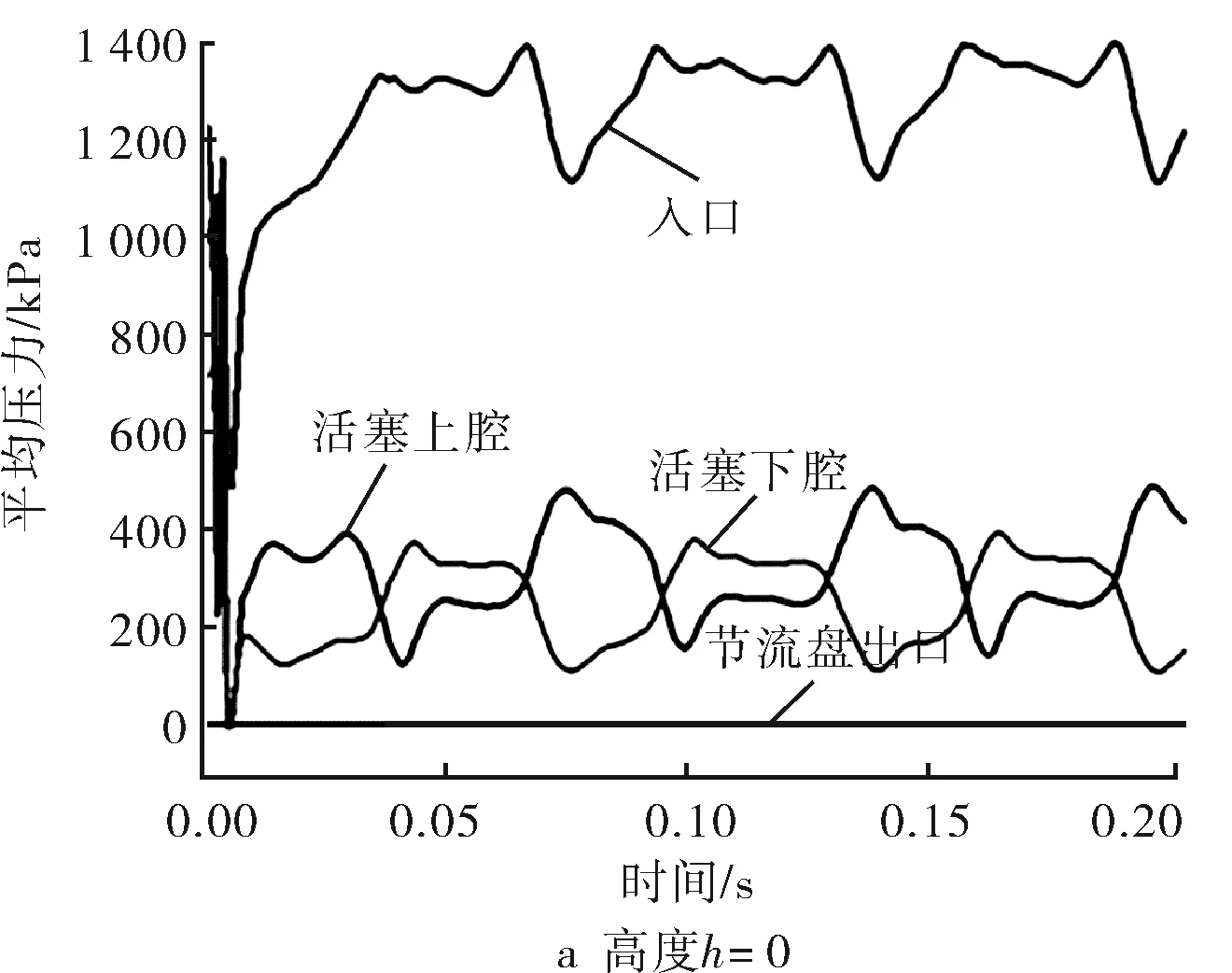
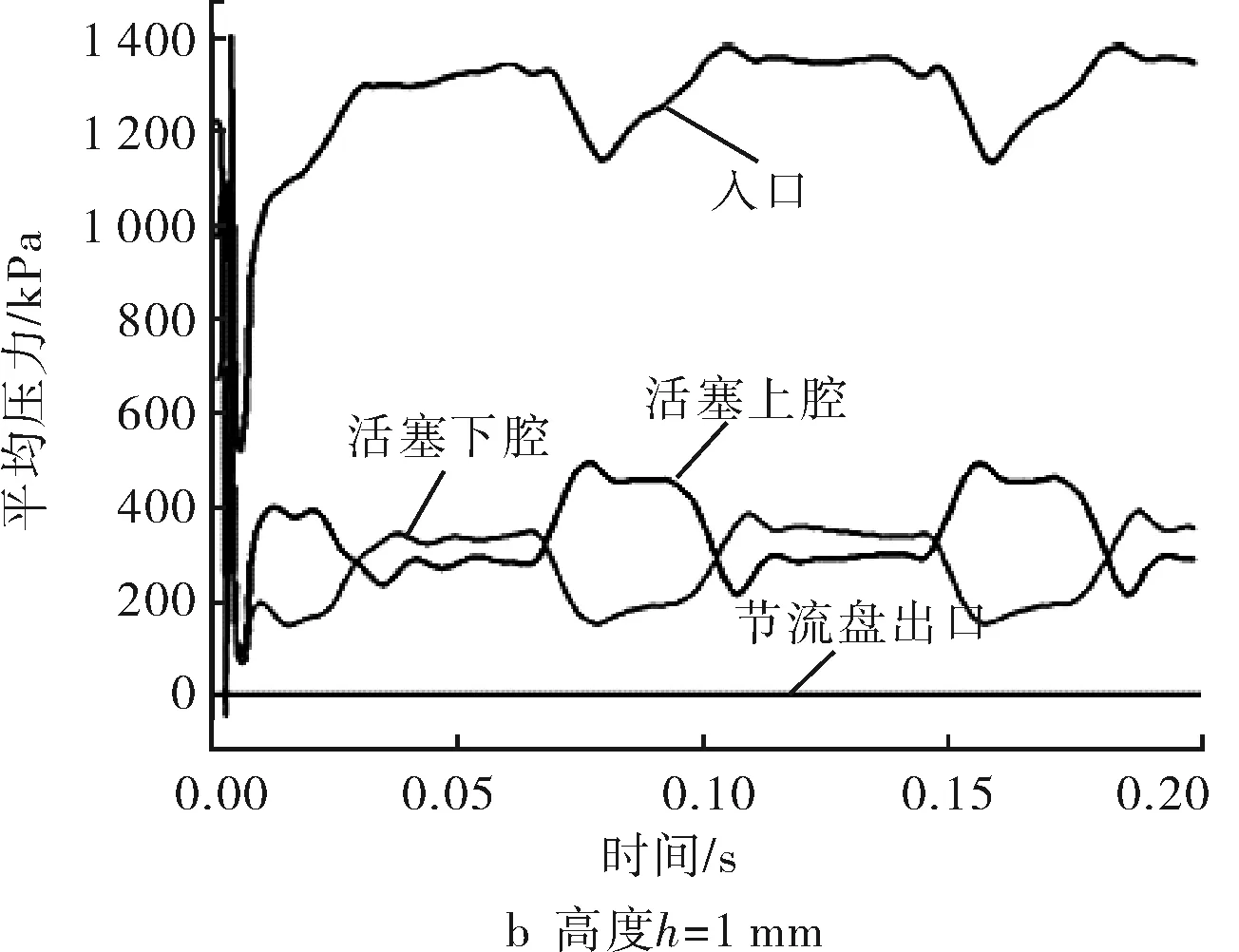

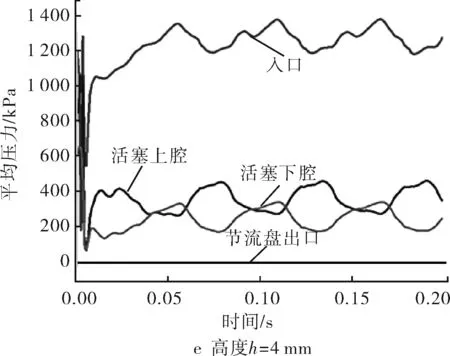
图8 侧壁高度影响的计算结果
根据图8压力随时间的变化过程可以看出,水力振荡器在最初极短的时间内起伏很大,并在左右迅速进入了稳定工作状态。入口处压力远高于其他位置压力。活塞上下腔压力变化呈周期交替起伏,且活塞上腔压强略高于活塞下腔,主要因为流体进入活塞下腔需经过的流道更长。随着侧壁高度的不断增大,活塞下腔压强高于上腔阶段的时间明显变短,侧壁高度的变化对振荡周期长短也有很大影响。由于活塞后端存在阶梯状,活塞杆随活塞周期运动并控制后端节流口开度,导致活塞上下腔压力在1个周期初有极短的陡增并迅速降低趋于平稳,这在一定程度上可以保护缸体减少活塞的冲击。随着振荡频率增加,这种特性也出现逐渐减小甚至消失的趋势,也说明不同的振荡器结构对压降和振荡频率存在影响。
总结4个影响因素分别对压降和振荡频率的影响,并进行数据分析,绘制得到各关键参数对水力振荡器的频率及压降的影响规律,如图9~12。
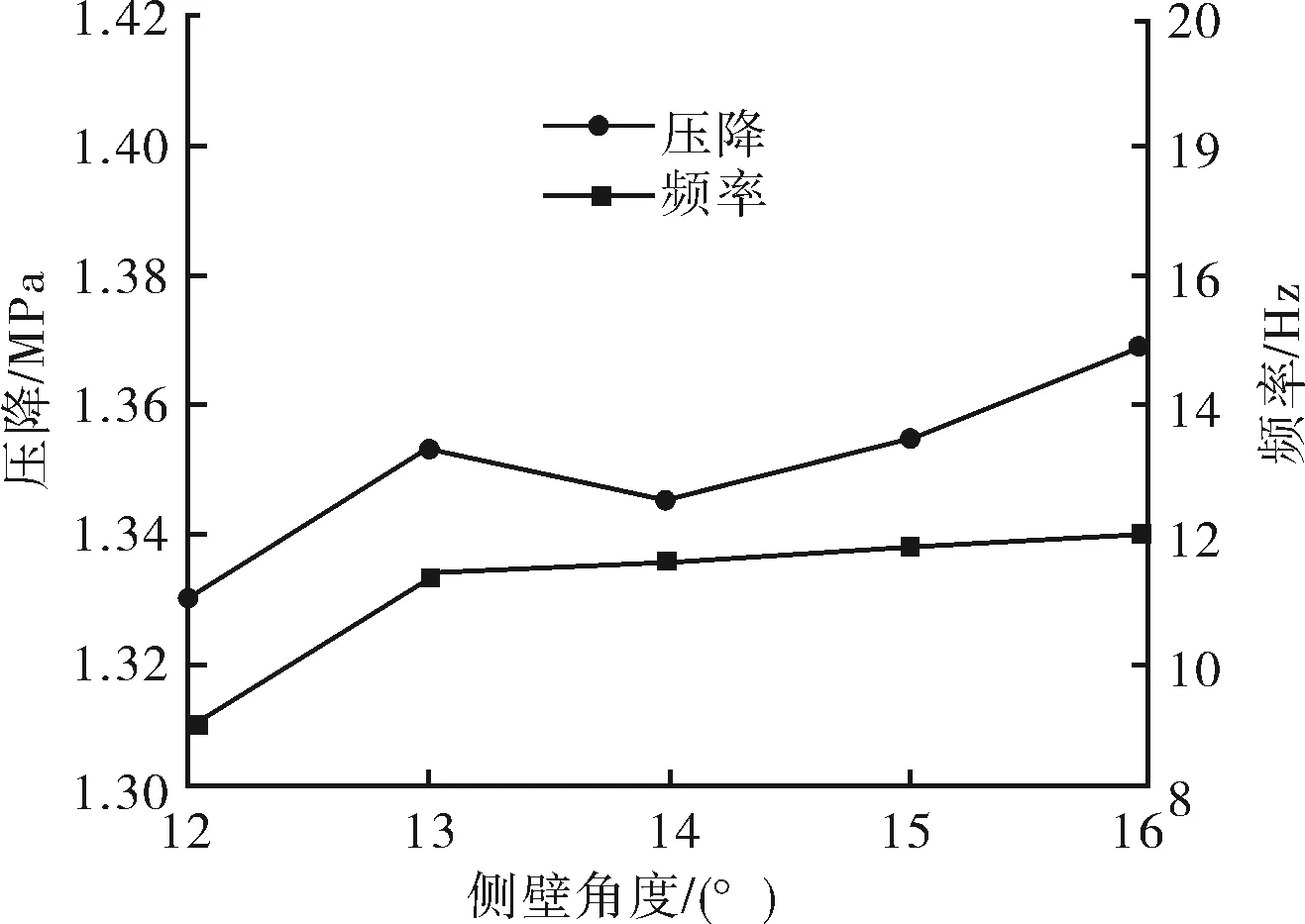
图9 侧壁角度对频率及压降的影响
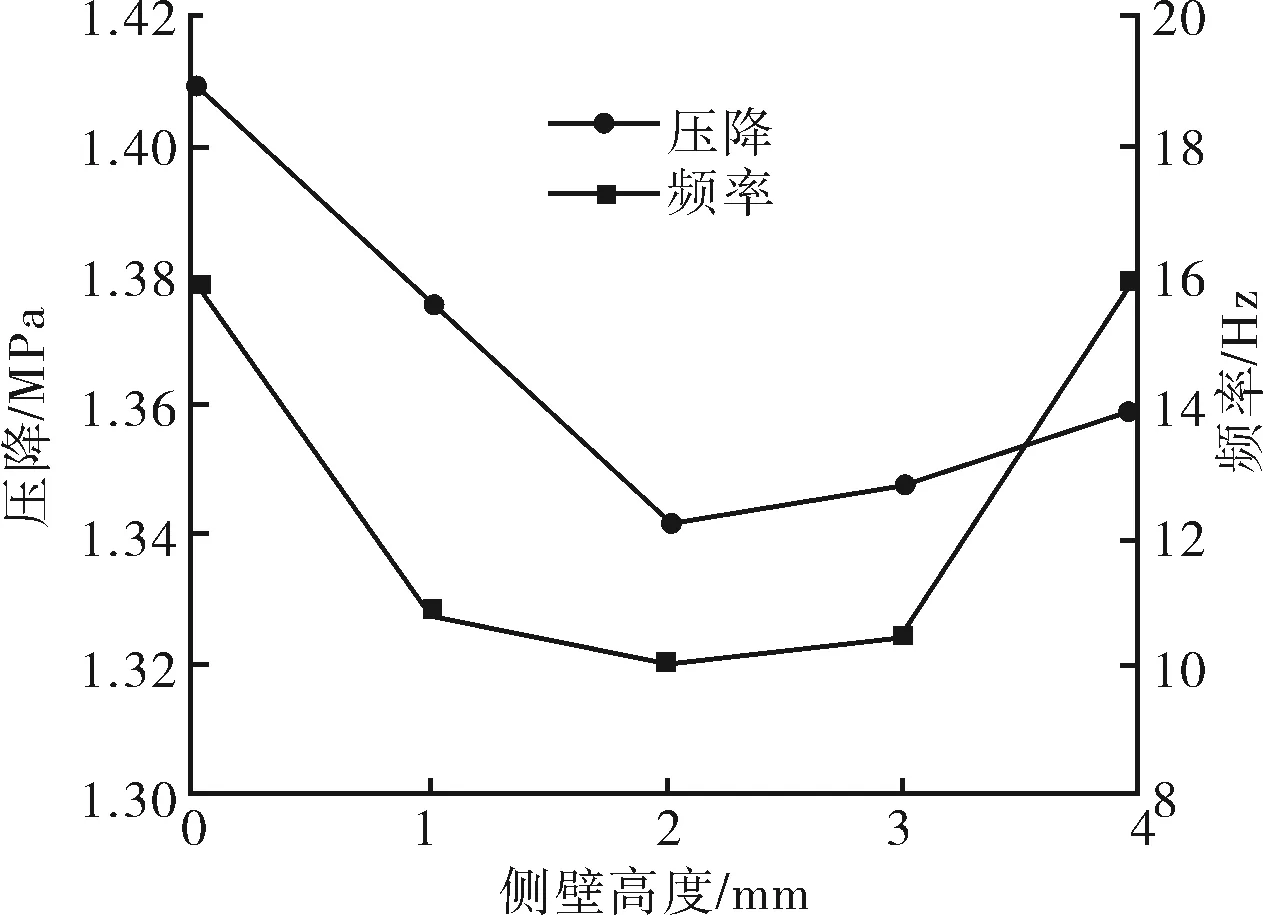
图10 侧壁高度对频率及压降的影响
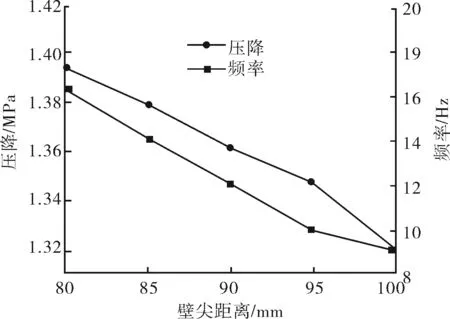
图11 劈尖距离对频率及压降的影响
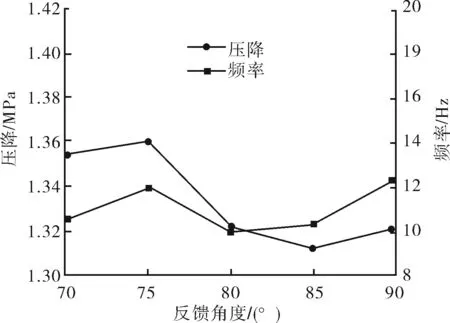
图12 反馈角度对频率和压降的影响
图9~12结果表明:
1) 随着侧壁角度增加,压降和振荡频率增大。压降在1.33~1.37 MPa,振荡频率在9~12 Hz,侧壁角度在12°,压降最小。原因是随着侧壁角度的增大,侧壁的附壁区域向侧壁后方移动,附壁切换变化更快。
2) 随着侧壁高度的增大,振荡频率和压降会出现先下降后升高的趋势。压降在1.34~1.41 MPa,振荡频率在10~16 Hz,侧壁高度为2 mm,压降和振荡频率最小。
3) 随着劈尖和射流口的距离增大,振荡频率和压降逐渐趋于减小。压降在1.32~1.38 MPa,振荡频率在9~16 Hz,劈尖距离为100 mm,压降最小。结果表明,劈尖可以改善射流附壁,劈尖在距离射流口更近的地方能更快促进射流附壁。
4) 随着反馈角度的增大,振荡频率和压降有先减小后增大的趋势。压降在1.31~1.36 MPa,振荡频率在10~12 Hz。说明在试验极限条件下,可以通过控制反馈角度来达到更低的压降。
3 结论
1) 运用单因素分析法和CFD数值模拟方法分析了结构参数对水力振荡器压降和振荡频率的影响。随着侧壁高度的增加,水力振荡器压降和振荡频率先降低随后上升,侧壁高度为2 mm时,压降和振荡频率达到最低值;随着侧壁角度增加,振荡器压降和振荡频率都有增加的趋势,并逐渐趋于稳定;随着劈尖距离的增加,水力振荡器压降和振荡频率呈下降趋势;反馈角度的变化对于压降和频率影响的敏感性并不强。
2) 确定了在不同影响因素下的最小压降,更为优化的结构有效帮助钻头改善钻压、提高钻井效率。新型水力振荡短节有效改善钻柱与井壁的摩擦环境,对降低摩擦、减小阻力有促进作用。
3) 新型水力振荡器在流量20 L/s工作环境下,以9~16 Hz脉冲频率稳定工作,工作准备时间短,响应速度快。相较于传统轴向振动减阻工具的平均压降4.135 MPa[8],新型水力振荡器压降更低,约为1.31~1.41 MPa,说明新型水力振荡器水力特性良好。
