一种基于ITA改进的水文气象序列趋势分析法

吴国栋，刘廷玺，薛河儒

(1.内蒙古农业大学计算机与信息工程学院，内蒙古 呼和浩特 010021；2.内蒙古农业大学理学院，内蒙古 呼和浩特 010018； 3.内蒙古农业大学水利与土木建筑工程学院，内蒙古 呼和浩特 010018)

由于气候的变化，在水资源规划、管理等研究中，对气温、径流、降水、蒸散发等数据序列在不同时间尺度(如年度、月度、季度等)的趋势识别、检测和评价成为近年来重要的研究内容[1-2]。目前，国内外学者就全球不同地区的水文气象要素开展了大量的趋势分析研究，基于不同的理论提出和发展了多种趋势分析方法[3-6]。总体而言，针对水文气象要素的时间序列在时域上的趋势分析方法包括两大类：参数型趋势检测法和非参数型趋势检测法。参数型趋势检测方法主要有线性回归、滑动平均、累积距平等方法，而Sen斜率估计、Mann-Kendall秩次检验等属于非参数型趋势检测方法。

近30年来，相关研究人员采用Mann-Kendall秩次检验法(MK法)开展了很多关于环境大气、水文、气象和农业等方面的研究。MK法是一种应用广泛的非参数型趋势检测法[7-10]，不仅可以探测时间序列所蕴含趋势的增减性，还可以从统计学角度分析趋势的显著性水平，具有简单易操作、结果可信度高的特点，而且不受限于数据的概率分布。2012年，Sen[11]提出一种改进的非参数型趋势检测法，即ITA(innovative trend analysis)法。ITA法是从图形上直观地观察数据序列的趋势。由于ITA的直观性和对数据独立性及分布规律无要求，所以受到广泛关注和应用[9，11-15]。ITA法不仅可以从整体上观察数据序列，还可以分开研究数据在低值区、中值区和高值区等不同数据区域的变化趋势[12]。Sen[16]在2017年补充了ITA法的趋势指标及其显著性检验方法，使得ITA法的功能更加完善。

虽然ITA法是一种易用、直观的趋势检测方法，但由于其为参数型检测方法，这使得其结果会受到数据序列分布特征的影响。本文基于ITA法设计一种新的趋势统计量，采用非参数统计方法——自举法[17-18](Bootstrap)进行显著性检验。采用数值模拟方式分析多种人工数据序列，将改进的趋势检测法分别与经典的MK法和ITA法进行检测结果的一致性比较，验证其可行性。最后应用改进的趋势检测法对黑河上游年径流总量、日本福冈每年风暴天数、北京最大日降水量和琼海年均气温等4种时间序列数据进行趋势检测和显著性分析。

1 研究方法

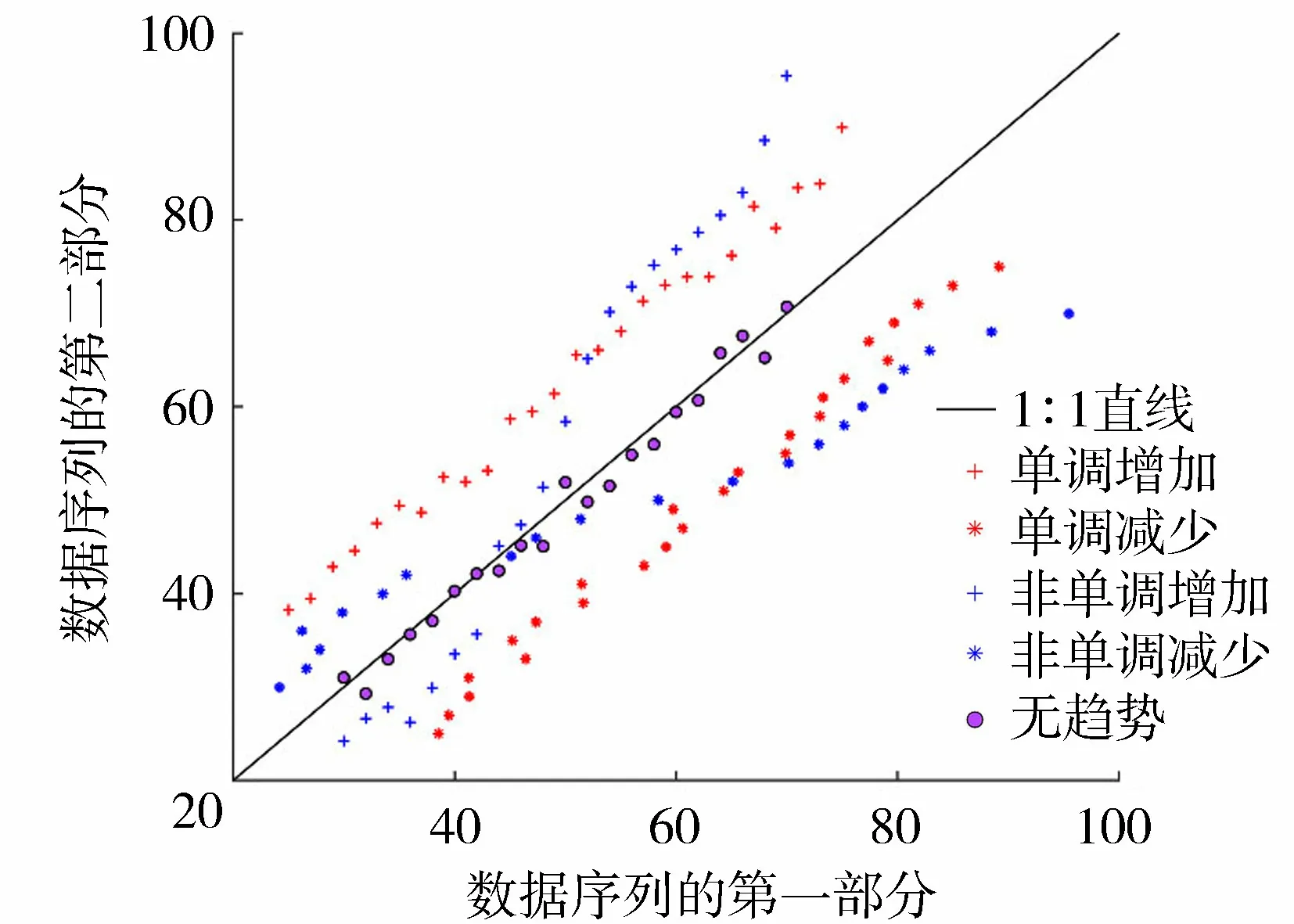
图1 ITA方法中的5种趋势类型Fig.1 Five kinds of trend according to ITA

ITA法是一种较为直观的趋势检测方法，通过它可以观察数据序列单调或非单调增加或减少趋势，共有5种情况：单调增加、非单调增加、单调减少、非单调减少和无趋势。ITA法的具体过程为：首先将数据序列平均分成相等的两部分，并分别按照升序排列，记为{y1i}和{y2i}(i=1，2，…，n/2)。然后在直角坐标系内以{y1i}为横坐标，{y2i}为纵坐标画出散点图并与无趋势直线(1∶1)进行比较(图1)。如果散点分布在45°线的上方，说明存在单调增加的趋势；如果散点分布在45°线的下方，说明存在单调减少的趋势；如果散点分布于45°线的附近，说明无趋势。而散点越远离45°线，说明趋势越明显。

2017年，Sen[13]又提出基于ITA法的趋势显著性检验方法，其统计量为

(1)

虽然ITA法可以在图形上直观地判断趋势的增减性和单调性，甚至可以观测在不同大小区间内数据序列的趋势，但是该方法在趋势的显著性检验中回到了参数性检验过程，趋势显著性结果必然会受到数据序列概率分布和数字特征的影响。而水文气象要素的变化往往存在较大的随机性，所以相应的时间序列服从何种概率分布难以确定，尤其在序列长度较小时。另外，水文气象要素时序数据记录的不可重复性，也增加了确定其概率分布的难度。Sen[13]提出ITA方法时，并没有给出非常严格的数学证明来说明按照标准正态分布对ZITA进行检验的合理性，因此考虑将ITA中的趋势显著性检验过程由参数型检验改为效果等同或更好的非参数型检验过程。

自举法是非参数统计应用中对统计量进行区间估计的重要方法之一，是现代统计学中依托计算机高速发展并被广泛应用的一种重抽样技术。其基本原理是在一个样本中进行多次有放回的均匀采样，生成一系列能够代表研究总体的多个样本，然后再根据抽出的样本计算统计量。按此过程可以生成关于待检验统计量的一个经验分布，便可估计其置信区间来进行统计推断。自举法的优点是对样本的概率分布没有任何要求，且无需增加更多的样本信息就可以对统计量进行准确的统计推断，这与水文气象要素序列的随机性和数据的不可重复性完全契合。

另一方面，根据ITA法的原理，散点分布越远离无趋势直线，趋势越明显。为了更好地说明散点偏离无趋势直线的程度，采用相对距离作为衡量趋势及显著性的新指标。

综上，在ITA法的基础上，引入一个新指标P检测趋势的增减性，并用自举法确定其显著性：

(2)

具体过程描述如下：

a.将时间序列数据{xi}(i=1，2，…，n)平分为两段，按升序排列后记为{y1i}和{y2i}，并计算P。

b.在{xi}(i=1，2，…，n)中进行有放回的重采样，即从序列{xi}中依次等概率地随机抽取n个数据(其中有的数据可能会被多次抽到)构成一个新时间序列样本，详细计算过程可参考文献[18]。重复采样M次后生成M个长度为n的新序列，对每个新序列重复步骤a，并将得到的新指标按照升序排列：P1，P2，…，PM。

c.考虑置信水平α，计算

L=Mα/2H=M(1-α/2)

(3)

则置信区间为[PL，PH]。如，M=1 000，α=0.05，则L=25，H=975。从升序排列P1，P2，…，P1 000中找到第25和第975位置的两个数P25和P975，则原始序列{xi}的新指标P在置信水平为0.05上的置信区间为[P25，P975]。

d.如果{xi}(i=1，2，3，…,n)的P落入置信区间，则认为在α置信水平上趋势不具有显著性，反之，认为有显著性，且P>0代表增趋势，P<0代表减趋势。

自举法是在未知序列分布规律的情况下进行显著性检验的有效办法，Mailhot等[19]指出，M=1 000可以保证结果的可靠性，本文选择M=5 000进行计算。

2 数值模拟验证

为了验证改进的趋势检测法的可行性，人工生成一阶自回归随机过程数据序列进行蒙特卡罗模拟。按式(4)生成长度为n的数据序列：

(4)

式中：μ为平均值；ρ为一阶序列相关系数；εi为服从标准正态分布的随机扰动。然后根据{Xi+d·i}(i=1，2，…，n)嵌入斜率为d的线性趋势。

利用改进的趋势检测法与MK法(具体过程可参考文献[7]或[9])和ITA法分别对人造序列进行趋势和显著性检验，并记录结果。在相同的参数设定下，重复多次后统计改进的趋势检测法与MK法和ITA法检测结果的一致率。如，当μ=20，σ=5，按序列的相关系数ρ=0、±0.1、±0.5、±0.9以及植入的线性趋势斜率d=0.01、±0.05、±0.09组合生成共35种参数数据序列，每种参数序列各1 000条。对该1 000条数据序列分别进行MK法、ITA法和改进的趋势检测法的趋势检验，统计改进的趋势检测法分别与MK法和ITA法在趋势类型(增或减)、10%置信水平的趋势显著性检验结果的一致率，以及综合两方面检验结果的一致率，结果见表1。

检验结果表明：

a.改进的趋势检测法与MK法和ITA法一致率不受序列均值的影响。

b.序列中蕴含的趋势越强(d的绝对值越大)，3种方法的检测结果一致程度越大。

c.在趋势类型一致率方面，改进的趋势检测法与MK法的结果最大误差小于5%，与ITA法的结果最大误差小于1%。

d.在显著性一致率方面，只有当趋势较弱(d绝对值很小)且前后两个子序列存在强正相关时，出现一致率下降的现象。如，当d=±0.01、ρ=0.9时，一致率下降到90%以下。

在数值模拟过程中发现，ITA法的检验指标会受到数据序列的长度和标准差的影响，而改进的趋势检测法受其影响较小。总体而言，数据序列越长，改进的趋势检测法和ITA法的趋势显著性检验结果与MK法的结果越一致，且标准差越大时越需要更长的数据序列才能保证较高的一致率。相比而言，用改进的趋势检测法检验同样标准差的数据序列，达到指定的一致率所需的数据序列长度较小。换而言之，如果数据序列长度较小时(如小于100)，改进的趋势检测法的检验效果要优于ITA法。

表1 利用改进的趋势检测法与MK法和ITA法模拟结果比较

如当生成1 000条ρ=0、μ=50、σ=30、n=100的序列，并加入0.05的趋势斜率，分别用MK法和ITA法进行趋势检验。结果表明两种方法的趋势类型检验结果一致率为84.3%，而显著性检验结果的一致率只有25.9%。而针对同样的数据序列，改进的趋势检测法与MK法的趋势类型检验结果一致率可达到90.2%。图2反映了模拟过程中的1个数据序列，经MK法和改进的趋势检测法检验无显著趋势，但是ITA法的检验结果是在0.01的置信水平上显著负趋势。究其原因，可能是ITA法中的s与时间序列的平均值有关，当样本容量不大时均值易受数据序列中异常值的影响，造成均值不能很充分地代表样本的中心趋势。另外数据序列的标准差增大后，不仅加剧了异常值对均值的影响，而且也会影响ITA法显著性检验中的置信区间。事实上，根据该数据序列的正态分布Q-Q图可以确定其为非正态分布(图2(c))。由此可见，ITA法会受到时间序列分布特征和数据统计特征的影响而产生错误结果。但是改进的趋势检测法的趋势显著性检验过程完全是非参数化过程，显著性不易受到来源于数据序列的分布特征和统计特征的影响，所以检验结果与经典的MK法一致程度高。

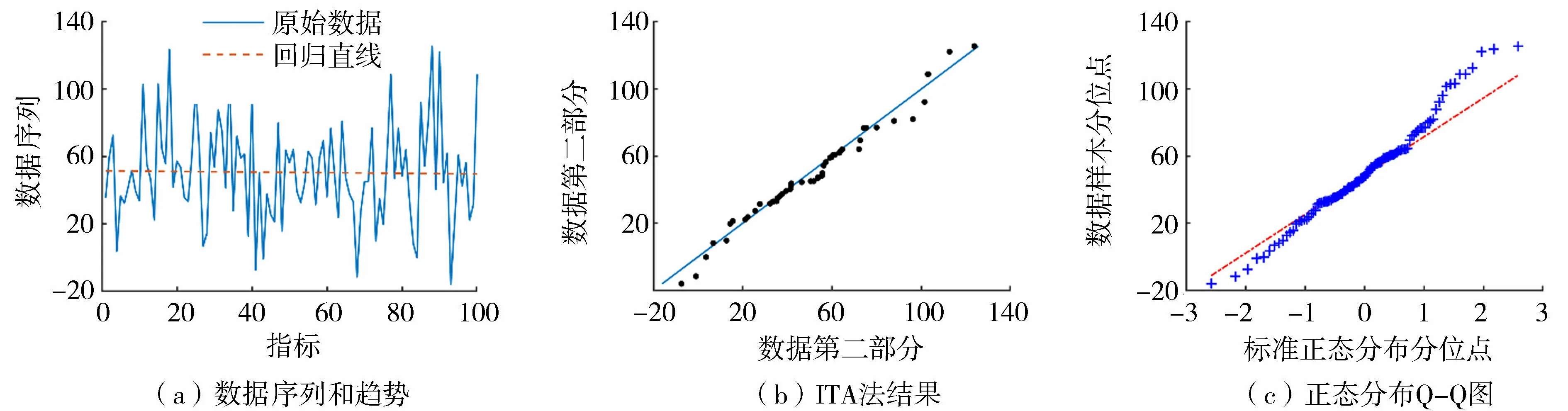
图2 一列ITA法与MK法结果差异大的数据Fig.2 A series with big differences between ITA and MK results

3 实例应用

将改进的趋势检测法应用于不同地区、不同长度、不同水文气象要素的数据序列。考虑数据的可获得性、序列长度、数据的完整性和水文气象要素的种类，对黑河上游(1891—2008年)的年径流量、日本福冈站(1948—2019年)年风暴天数、北京气象站(1952—2019年)年最大日降水量和琼海气象站(1954—2019年)年平均气温共4种时间序列进行分析。黑河上游的年径流量数据来源于国家冰川冻土沙漠科学数据中心 (http：//www.ncdc.ac.cn)；日本福冈站的数据来源于Tutiempo Network(https：//en.tutiempo.net)，个别缺失数据经3次样条插值做了补充；北京气象站和琼海气象站的数据来源于国家气象科学数据中心(http：//data.cma.cn)。4个时间序列的基本信息和统计特征信息见表2、表3。

表2 时间序列基本信息

表3 时间序列统计特征信息

为了直观反映各数据序列的平均趋势，将每个数据序列及其线性回归直线合并成图3，同时将检测结果汇总，见表4。

图3 4个时间序列的数据分布及回归斜率Fig.3 Data distribution and regression slope of four time series

表4 4个时间序列的趋势检测结果

黑河上游年径流量在0.05的显著性水平上具有显著的增加趋势，解阳阳等[20-21]应用MK法也得出了相同的结论，并指出黑河上游径流量增加的主要原因是降水量和平均气温的增加。Zhang等[22]研究了近50年北京市暴雨趋势及其空间差异，采用MK法检验得到的结论表明，北京市年最大日降雨量只在0.1的显著性水平上呈现显著下降的趋势，该结论与改进的趋势检测法的检验结果完全一致。孙瑞等[23]同样采用MK法研究了1959—2013年海南岛气象要素的时空分布特征，结果显示海南岛平均气温的年际增长趋势通过了0.01显著性水平检验，这与本文检验的琼海气象站年均气温记录在0.01显著性水平上具有显著增加趋势的结论一致。日本福冈站的年风暴天数时间序列也表现出与琼海气象站年均气温相同显著性水平的增加趋势(表4)。

4 结 论

a.改进的趋势检测法是一种非参数型趋势检测方法，检测结果与经典的MK法保持高一致率，表明了改进的趋势检测法的可行性。

b.改进的趋势检测法不受限于数据序列的分布特征，在数据序列方差较大或数据系列长度较小时仍能保证与MK法良好的一致性，优于ITA法。

c.在数据序列蕴含的趋势斜率很小且正相关系数很大时，检测结果的一致性会受到一定的影响，原因需进一步研究。

d.经实际应用，黑河上游的年径流量呈高显著性水平(5%)的增加趋势，日本福冈每年发生风暴的天数呈现高显著性水平的增加趋势，北京的最大日降水量是中等显著性水平(10%)的下降趋势，琼海的年平均气温表现为高显著性水平的上升趋势。