改进遗传算法的RBF神经网络控制研究＊

周勇

（荆州学院信息工程学院，湖北 荆州 434020）

RBF（径向基函数）神经网络是具有单隐层的一种三层前向神经网络，其具有网络结构简单、学习速度快、逼近能力强等特点，在系统辨识、函数逼近、模式识别等领域得到广泛应用。RBF神经网络具有模拟人脑中局部调整、相互覆盖接收域的神经网络结构，能以任意精度逼近任一连续函数[1]，一直是研究的热点之一。RBF神经网络在学习过程中，其性能主要取决于隐层神经元基函数中心、宽度和隐层节点到输出层之间的连接权值的整定。目前，RBF神经网络的参数整定方法主要有K均值聚类方法、梯度下降法、粒子群算[2]、进化算法[3]等，其中，普通梯度下降法在训练过程中极易出现振荡、不稳定的情况，而且实时性和鲁棒性较差[4]。其他方法如粒子群算法、进化算法等，虽然有一定的全局收敛能力，但收敛速度慢，网络计算代价大。遗传算法（Genetic Algorithm，GA）是一种高度并行的随机优化方法，具有很好的全局搜索能力和鲁棒性，然而，遗传算法虽然应用广泛，但在解决复杂问题时，由于其自身的随机搜索特点也带来了收敛速度慢和算法局部收敛（早熟）等问题[5]。本文在前人研究的基础上，结合改进的遗传算法提出一种改进遗传算法优化的RBF神经网络控制器，通过系统辨识仿真分析，验证了其参数优化效果。

1 RBF神经网络

RBF神经网络模拟人脑中局部调整、相互覆盖接收域的神经网络结构，是一种具有单隐层的三层全局逼近性能的前馈网络。RBF神经网络在结构具有从输入层到隐含层的高斯非线性关系和隐含层到输出层的权值线性关系，从而使网络学习快速易行，避免了局部最优的问题。RBF神经网络结构如图1所示。

图1 RBF神经网络结构

RBF神经网络一般由3层构成，即输入层、隐含层和输出层，其中输入层节点主要负责传递输入信号到隐含层，隐含层节点由高斯函数组成，对输入的信号产生局部响应，即当输入信号接近高斯函数的中央范围时，隐含层节点产出较大输出，输出层节点为各隐含层的输出加权和，隐含层到输出层之间的权值可调。

RBF神经网络的学习包括两部分：一是高斯函数中心和宽度的确定，另一个是输出层权值的确定。给定网络输入X=（x1，x2，…，xn）为n维向量，RBF神经网络的输入层到隐含层实现x→h（x）的非线性映射，即隐含层的变换函数h（x）为一个径向基函数，其径向基函数最常采用高斯函数，则RBF神经网络隐含层第j个节点的输出为：

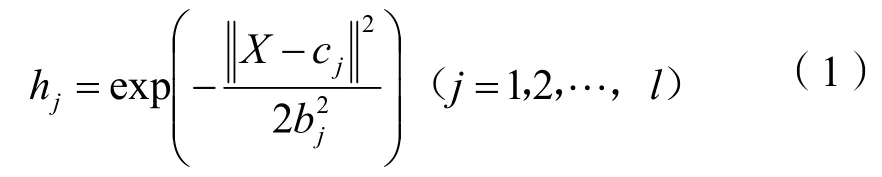
式（1）中：cj和bj分别为第j个隐含层节点的高斯函数中心和基宽参数，bj为大于零的数，它决定了该基函数曲线围绕中心点的宽度；l为隐含层节点的个数。

假设wj为第j个隐含层节点到输出层的加权系数（权值），则RBF神经网络的隐含层到输出层实现h（x）→yk的线性映射，即：

式（2）中：yk为第k个节点的输出；m为输出层的节点数。

RBF神经网络的学习过程是将采集到的数据样本对神经网络进行训练，不断调整基函数中心c、宽度b和权值w使网络总均方误差为最小，即对于N个训练样本，RBF神经网络的希望输出为d，则总均方误差函数为：

式（3）中：N为样本对数；m为网络输出节点数；dpk为第k个输出节点在第l个样本的希望输出；ypk为第k个输出节点在第p个样本的实际输出。

2 改进遗传算法优化RBF神经网络的实现

遗传算法（Genetic Algorithm，GA）是美国Holland教授于1975年首先提出来的一种借鉴生物进化理论和门德尔基因遗传理论的高度并行、随机的优化方法[6]。在遗传算法中，交叉和变异算子是算法进化的核心，其交叉率Pc和变异率Pm是算法收敛和稳定的关键参数。交叉算子是通过基因重组来获取优良个体，决定了遗传算法的全局搜索能力[7]。变异算子是通过改变群体个体基因，使群体具有较好的多样性，克服早熟。遗传算法的Pc和Pm反映了算法交叉和变异操作的概率，决定了算法的收敛性能。标准遗传算法因为随机搜索的特点，在进化过程中，其Pc和Pm恒定不变，收敛性能较差。结合文献[8]，本文引入一种改进的遗传算法，使算法的Pc按Sigmoid函数变化，变异率Pm自适应按进化代数变化，提高算法的全局搜索能力和收敛速度。

改进遗传算法优化RBF神经网络参数步骤如下。

第一步，编码及初始化群体。选择高斯函数中心c、基宽参数b和连接权值w为优化参数，实数编码，并根据种群规模产生初始群体为[0，1]之间的随机数。

第二步，解码，计算种群个体适应度，确定适应度函数F，评价是否满足收敛条件。目标函数求最大值，则F=f（x），否则，F=1/f（x）。同时，对个体适应度按从小到大进行排序，选出最大个体适应度。改进遗传算法的适应度函数为F=1/J，J为均方误差函数E，即f=1/E。

第三步，如果满足要求（精度1e-5或进化代数T），输出结果；否则继续第四步。

第四步，设计遗传算子。本设计采用轮盘赌的选择方法，算术交叉和均匀变异的遗传算子，为了防止遗传算法的早熟和收敛较差的问题出现，采用改进的自适应交叉概率和变异概率，将S曲线变化模式和进化代数用于交叉概率和变异概率，使个体的变异和交叉分别受进化代数和适应度的约束。改进的自适应调节公式和自适应变化曲线如式（4）（5）和图2、图3所示。

图2 交叉率调节曲线

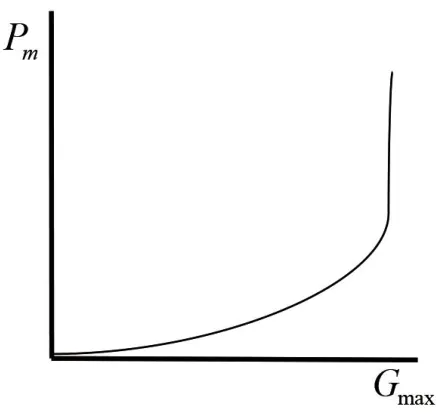
图3 变异率调节曲线

式（4）（5）中：Pcmax、Pcmin分别为交叉率的最大值和最小值；f'为要交叉的2个个体中较大的适应度值；k1为曲线平滑参数，用来调节曲线的光滑程度；favg为种群的平均个体适应度值；fmax为种群中最大的个体适应度值；Pm1、Pm2和Pm3都是正实数；Gmax为最大进化代数；G为当前进化代数。

由图2、图3和改进的公式（4）（5）可知，Pc按照个体适应度在favg和fmax之间随S曲线进行非线性调整，Pm按进化代数进行非线性调整。在种群进化初期，保证了当前种群优良个体Pc和Pm较小，使算法收敛速度变慢。同时，随着进化代数的增加，当大多数个体适应度与favg接近时，使个体Pc最大，进化代数最大时Pm也趋近于最大，避免了算法停滞不前。在个体适应度接近fmax时，尽可能缓慢地减小个体Pc，使Pc最小，最大限度地保留favg处的优良个体，克服算法早熟和局部收敛。

第五步，根据favg、个体适应度和进化代数，结合自适应调节公式进行交叉和变异操作。

第六步，返回第二步，如达到指定要求，算法结束，否则继续执行操作。

改进遗传算法RBF参数优化流程如图4所示。

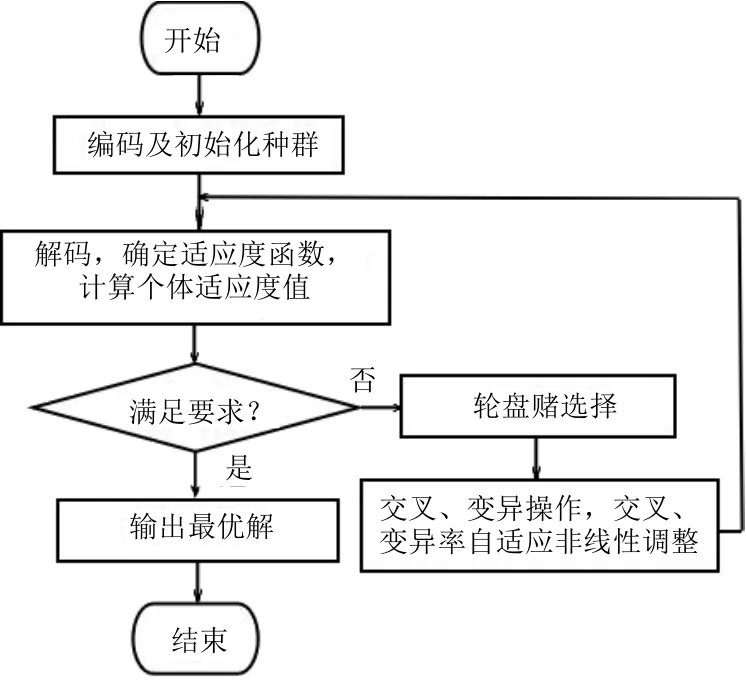
图4 改进遗传算法RBF参数优化流程图

3 实验及结果分析

为了研究改进遗传算法优化RBF神经网络的性能，将该算法应用于一个典型的非线性系统的辨识，通过函数逼近能力来说明该方法的实用性和合理性。为了比较，同时采用梯度下降法来训练RBF网络，所有算法程序均采用MATLAB语言编程，非线性系统模型为：

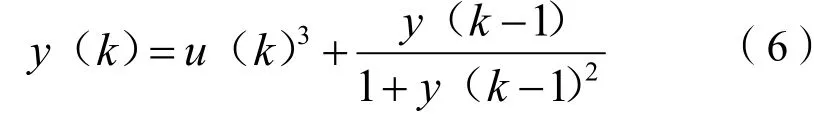
3.1 算法参数选择

改进遗传算法参数如表1所示。

表1 改进遗传算法参数设置

其中，在遗传算法优化中，种群规模为30，最大进化代数为250代。由式（6）可知，y（k）与历史输出y（k-1）和u（k）有关，因此RBF神经网络输入x（k）定义为[y（k-1），u（k）]T，选择隐含层个数为20，因此RBF神经网络结构为2-20-1。

3.2 仿真结果分析

用于测试的RBF神经网络辨识中，取输入信号为正弦信号：u（k）=sin（10πt），得到300个学习样本（输入输出对），前100样本个训练RBF神经网络模型，后200个样本作为测试样本。改进遗传算法优化均方误差曲线如图5所示，当输入为u（k）=sin（10πt）时，采用改进遗传算法优化RBF神经网络时，网络经过120代后，均方误差为0.013 4，不再发生变化，基本达到误差要求，能较好地克服基本遗传算法学习时间长、收敛速度慢等缺点。曲线拟合分别如图6、图7所示，图中虚线表示实际输出有ym，实线表示目标输出y。

图5 改进遗传算法优化均方误差曲线

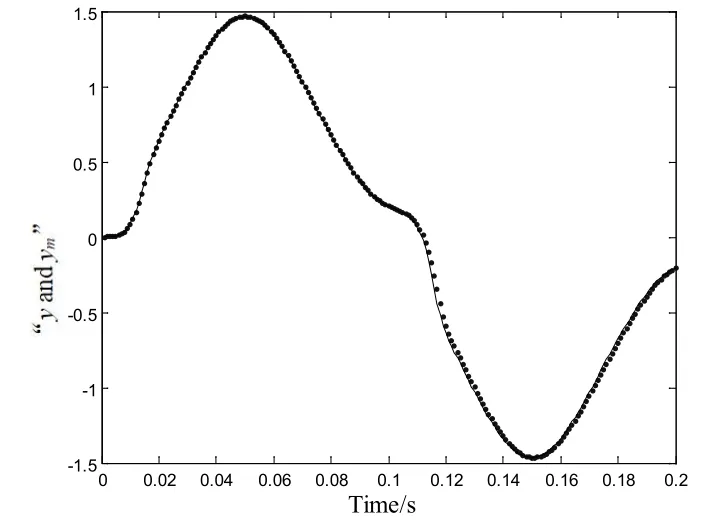
图6 改进遗传算法优化RBF神经网络的曲线拟合

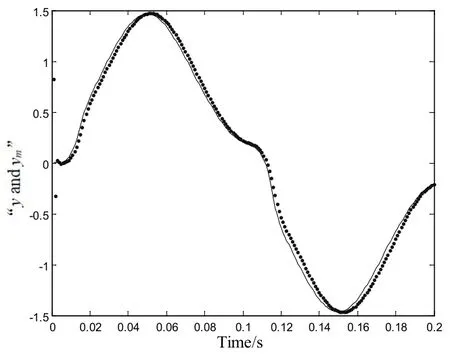
图7 梯度下降法的曲线拟合

由图6和图7可知，改进遗传算法优化后的RBF神经网络实际输出数据与目标数据基本吻合，符合函数的总体趋势，拟合效果优良，而采用梯度下降法优化RBF神经网络时，在初始和结束拟合时有一些发散，且在中间的数据拟合偏差较大。可见应用改进遗传算法优化的RBF神经网络控制器有着更强的优化效果。

4 结语

针对常规RBF网络学习算法的不足，提出一种改进遗传算法优化RBF神经网络的参数，利用改进遗传算法实现高斯函数的中心c、基宽参数b和连接权值w的选择。在改进遗传算法中，着重对交叉率和变异率的非线性自适应调节进行了设计。通过对典型非线性函数的仿真分析，本文提出的改进遗传算法优化的RBF神经网络控制器有着较好的优良性能，为实际工程应用提供了理论支持和有效途径。