满足本地差分隐私的分类变换扰动机制

朱素霞 王 蕾 孙广路

(哈尔滨理工大学计算机科学与技术学院 哈尔滨 150080) (哈尔滨理工大学信息安全与智能技术研究中心 哈尔滨 150080)

随着云计算和大数据技术的发展，用户端产生的海量数据被服务器收集起来进行各种数据分析任务.虽然对这些数据进行分析可以为人们带来可观的效益，但是却造成了用户隐私暴露的问题.差分隐私由于其强大的隐私保障已经成为了一种标准的隐私保护模型.随着差分隐私的广泛使用，服务器变得越来越重要.然而，在真实世界中保证所有服务器都是可信的是不实际的，而不可信的服务器可能会因为某些原因泄露用户的隐私.为了解决这一问题，本地差分隐私作为一种新的隐私保护技术被提出用来保护用户的隐私，其最典型的扰动机制是随机响应机制.在本地差分隐私中，服务器假设是不可信的，每个用户端对本地数据进行扰动使其满足本地差分隐私，然后再将扰动后的数据发送给服务器.服务器对收集的噪声数据进行计算，得到所需的统计信息.本地差分隐私方法可以在获得较为准确的统计信息的同时有效地对用户的数据进行保护，从而避免了用户隐私泄露的问题.

本地差分隐私由于其强大的隐私保证，已经被运用到很多实际的工作任务中.例如谷歌的Chrome浏览器使用的RAPPOR(randomized aggregatable privacy-preserving ordinal response)方法以及微软的遥测数据采集.这些方法使得在保护用户隐私的同时，可以利用用户的数据进行分析得到有效的统计结果.人们针对不同的数据类型提出了适用于不同计算任务的本地差分隐私框架，目前主要研究的统计任务有均值估计和频率估计.例如，谷歌Chrome使用的RAPPOR方法是针对分类型数据的频率估计，Nguyên等人提出了针对离散型数据的均值估计的扰动方法Harmony. Ye等人针对键值数据类型提出了PrivKVM方法，可以在满足本地差分隐私的同时估计键的频率以及键对应的所有值的均值.针对连续型数值数据的均值估计，Duchi等人的方法对数据进行扰动之后一共有2种可能得到的扰动值.由于这2种扰动值的绝对值都大于1，即不管隐私预算如何变化，其方差始终大于1.所以当隐私预算比较大时，该方法得到的均值估计的准确性相比于拉普拉斯方法要更差.随后，Wang等人针对Duchi方法的缺点，提出了分段机制(piecewise mechanism, PM).该机制不同的是，其扰动输出为一段连续值，且这段连续值的中间部分有更高的概率输出.虽然分段机制改善了Duchi方法中存在的问题，但是当隐私预算较小时，该方法并没有很好地提高均值估计的准确性，其最坏情况下噪声方差仍与Duchi方法接近.

除此之外，机器学习作为当前比较热门的学习领域，其中也涉及了大量用户的隐私保护问题.为了更好地保护用户的隐私，可以将其与本地差分隐私的相关扰动机制结合使用.目前，机器学习中较常使用的隐私保护方式是在模型训练时对用户梯度进行扰动，服务器收集扰动后的梯度进行更新.例如，Nguyên等人将Harmony运用到了随机梯度下降中，对每次迭代的梯度进行扰动，并且证明了本地差分隐私下的小批量梯度下降要优于随机梯度下降.Wang等人则利用多维数据扰动的方式，将分段机制用于迭代中的梯度扰动.这些方法虽然在机器学习训练过程中保护了用户的隐私，但由于机制本身的缺点，其训练结果的准确性仍然具有提升空间.

为了改善已有扰动方法引入的准确性问题，论文针对连续型数值数据，提出了一种满足本地差分隐私的分类变换扰动机制(differential classified transformation, DCT).跟已有的方法直接对所属数据类型使用对应的扰动方法进行扰动不同，本文提出的方法首先对数据类型进行了转换，将数值型数据转换为了1维二元分类数据，再对分类数据进行扰动.在真实数据以及合成数据中使用该方法进行均值估计，与已有的方法进行对比，可以得到一个更为准确的估计结果.在机器学习的隐私保护中，考虑到本地差分隐私中隐私预算的分配问题，为了在训练中得到更为准确的结果，论文将提出的分类变换机制用于构建满足本地差分隐私的小批量梯度下降，并在该框架下进行线性回归的学习任务.

总的来说，本文主要贡献如下：

1) 提出了一种数据变换扰动方法，并且得到了较好的结果，这给本地差分隐私的扰动提供了一个新方向，可以通过变换数据，使其在提高数据的可用性的同时又保障了用户的隐私；

2) 提出的分类变换机制具有良好的性能，在满足本地差分隐私保证的同时，在均值估计方面可以得到更为准确的结果；

3) 将提出的方法用于构建小批量梯度下降算法，并用该算法完成线性回归的学习任务，使得参与用户的数据受到良好保护的同时，可以得到一个较为准确的模型结果；

4) 在真实的数据集以及合成的数据集上进行实验，以对提出的机制进行评估.实验结果表明，不管是在均值估计还是在经验风险最小化任务中，使用分类变换扰动机制得到的结果误差要小于已有的方法.

1 相关定义

1.1 本地差分隐私

在本地差分隐私中，服务器收集各个用户的数据，并利用数据计算得到所需的统计信息.用户在将数据发送给服务器前，先对本地的数据进行扰动，再将扰动后的数据发送给服务器.服务器无法根据收集的噪声数据来获得用户的隐私信息.隐私预算的大小代表了用户隐私保护程度的强弱，其控制了隐私和效用之间的平衡，一个更小的隐私预算代表了更强的隐私保护程度.本地差分隐私的定义如下：

定义1.

ε

-本地差分隐私

.

随机函数

M

满足

ε

-本地差分隐私当且仅当域

M

中的任意2个输入

t

,

t

′以及对于

M

中的任意可能的输出

t

，有：

Pr

(

M

(

t

)=

t

)≤e×

Pr

(

M

(

t

′)=

t

),

(1)

其中

Pr

(·)代表概率

.

本地差分隐私作为差分隐私的分支，提供了比差分隐私还要强大的隐私保障

.

根据上面的隐私定义，服务器无论具备怎样的背景知识，都无法以高概率从接收到的用户的扰动元组

t

来判断用户的真实值是

t

还是

t

′

.

本地差分隐私中最经典的方法是随机响应机制，该方法主要用来收集用户的敏感数据以获得准确的统计信息，下面举例来介绍这个机制

.

假设服务器想知道有多少个用户是抽烟的，它会向每个用户发送问题“你抽烟吗？”用户接受到问题后采用抛硬币的方法来决定它的答案

.

假如硬币的正面朝上，那么用户将真实答案告诉服务器，否则的话它将告诉服务器一个相反的答案

.

使用该方法，服务器可以根据所有用户的回答得到一个无偏估计

.

假设每个用户抛硬币正面朝上的概率为

p

，即用户正确回答服务器的概率为

p

，则其提供错误答案的概率为1-

p.

为了使该方法满足

ε

-本地差分隐私，概率

p

应满足式(2)：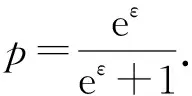

(2)

1.2 问题定义

论文主要研究的问题是连续型数值的均值估计，为了后续研究方便，这里简单假设每个用户

u

都有1个数值型数据

v

，本文所有使用到的符号如表1所示:

Table 1 Symbol Definition表1 符号定义

在本地差分隐私中，不同用户可以根据需求使用不同的隐私预算

ε

来保护自己的隐私

.

在本文中，为了便于分析，假设了一个统一的隐私预算参数值

ε

，目标是在满足

ε

-本地差分隐私的条件下完成下列2种类型的分析任务：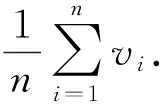

2) 经验风险最小化

.

论文中主要将线性回归及小批量梯度下降结合使用，并计算模型训练结果的均方误差来评估方法性能

.

2 数值数据的均值估计

均值估计是目前本地差分隐私中主要进行研究的统计任务之一，它在统计分析中具有重要作用.本节主要讨论在满足

ε

-本地差分隐私的条件下收集用户的数据进行数值属性均值估计的问题，对2种已有的方法进行介绍.

1) Duchi方法

Duchi等人提出了在本地差分隐私下用来扰动1维数值型数据的方法，如算法1所示:

算法1.

Duchi等人的1维数值数据扰动方法.输入：

v

∈[-1,1]、隐私预算

ε

;

② if

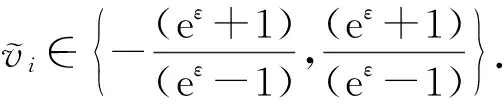
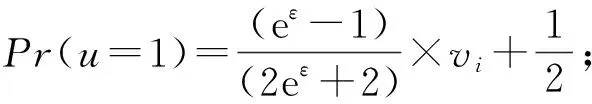
u

=1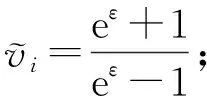

④ else

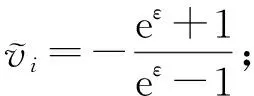
⑥ endif

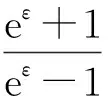
2) PM

Wang等人提出的分段机制PM是另一种在本地差分隐私下进行均值估计的扰动方法.与Duchi方法不同，PM分段抽取输入数值的扰动值.算法2描述了PM方法:

算法2.

PM数值扰动方法.输入：

v

∈[-1,1]、隐私预算

ε

;

① 从[0,1]中均匀随机抽取

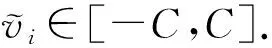
x

；

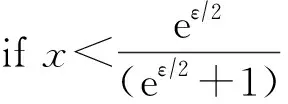
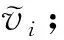
④ else

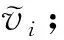
⑥ endif

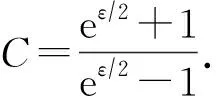
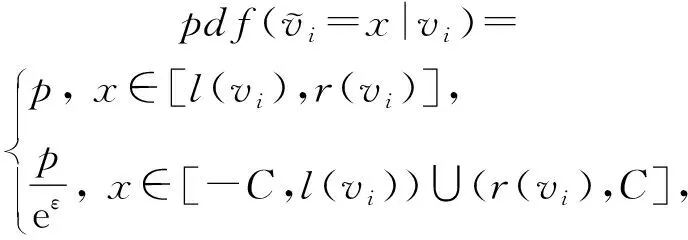
(3)

其中

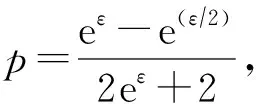
Wang等人证明了分段方法得到的扰动输出值为输入的无偏估计，并且将该方法用于均值估计能够得到比其他现有方法更为准确的结果.分段机制虽然改善了Duchi方法的缺点，当隐私预算较大时可以得到更为准确的结果.但是当隐私预算较小时，其最坏情况下的方差与Duchi方法的相近，准确性没有得到很好的提高.

虽然这2种方法对已有的方法进行了改善，一定程度上提高了连续数值型数据均值估计的准确性，但是仍然存在缺点，准确性仍具有较大的改善空间.如Duchi方法由于输出的扰动值的绝对值都大于1，所以在隐私预算较大时性能较差；而分段机制虽然对Duchi方法进行了改良，但是由于提出的分段机制在隐私预算较小时的最坏情况下方差与Duchi方法的接近，所以准确性在隐私预算较小时没有得到提升.

3 分类变换扰动机制

为进一步提高均值估计的准确性，本文提出了满足本地差分隐私的分类变换扰动机制，即DCT.与Duchi和PM直接根据无偏估计得到较为准确的结果不同，论文提出使用数据变换的方法使得在满足本地差分隐私的条件下可以得到更为准确的估计值.该机制不对原数据进行扰动，而是将数据先进行分类变换，对其转换后得到的1维二元分类数据进行扰动.对于分类变换扰动机制，其输入值

v

∈[-1,1]，扰动值的输出范围为[-

A

,

A

]，其中

A

=1+

d.

该机制主要分成3个阶段，分别是分类变换、分类扰动以及分类逆变换

.

3.1 分类变换

变换前需要对用户数据进行预处理，这里假设用户拥有的数据为浮点数

.

为了减少实验时的计算开销，方便后续的数据分析，将用户数据

v

标准化到[-1,1]

.

一般情况下，假设该属性的值域为[

L

,

U

]，式(4)给出了用户计算方式：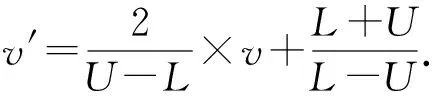

(4)

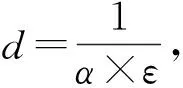
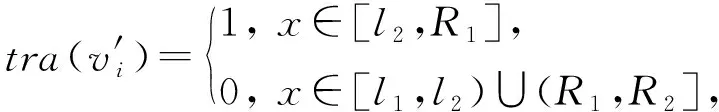
(5)

其中

l

=

v

′-

d

,

l

=

v

′-

m

,

R

=

v

′+

m

,

R

=

v

′+

d.

由于该数值位于扰动范围中心，所以在对数值型数据进行二值化时采用随机抽取的方式取值，即该数值对应的分类数值可能为1也可能为0

.

3.2 分类扰动

用户

u

的数据

v

已经转换为了1维二元分类数据，可以在本地直接使用随机扰动机制来对数据进行扰动

.

这里采用Xia等人提出的对单个位进行扰动的方法，式(6)给出了具体的扰动规则：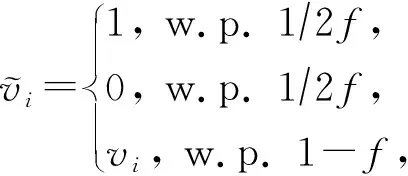

(6)

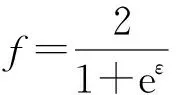
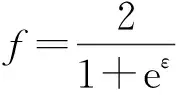
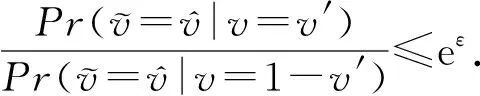
(7)

证明

.

根据式(6)，可以推得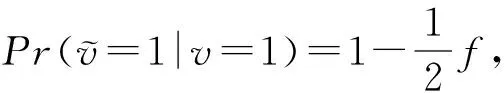

(8)

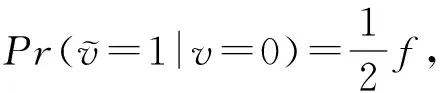
(9)

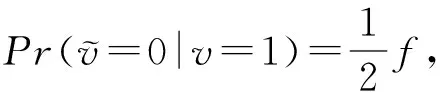
(10)

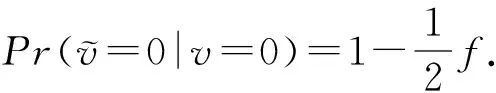
(11)

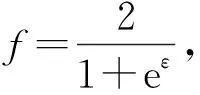
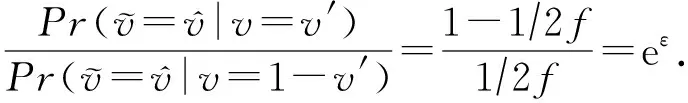
(12)

证毕

.

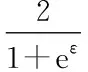
3.3 分类逆变换

对二元分类数据进行扰动之后，对其扰动输出值进行分类逆变换操作，输出数值型数据

.

转换规则为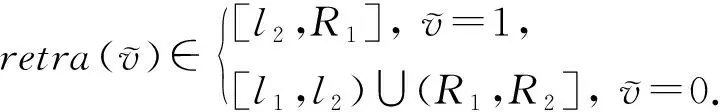

(13)

如果扰动后分类数据为1，则将其转换回数值数据时从中间的2段距离中随机均匀抽取1个值作为其转换后的值，如果分类数据为0则从两端的2段数据中进行均匀抽取

.

算法3.

分类变换扰动机制

.

输入：

v

∈[-1,1]、隐私预算

ε

;

① 从[0,1]随机均匀抽取

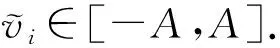
u

；② if

u

<0

.

5

④ else

⑥ endif

⑦ 从[0,1]中随机均匀抽取

x

;

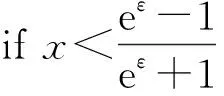
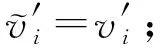
⑩ else

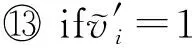
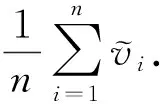
引理1.

算法3满足

ε

-本地差分隐私

.

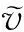
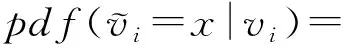
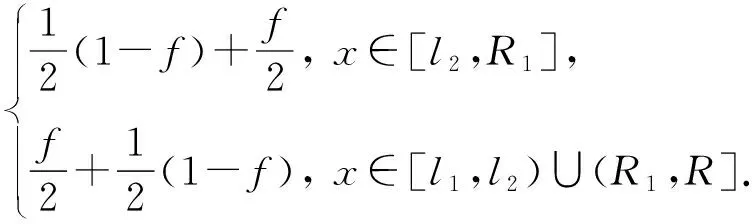
(14)

证毕

.

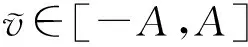
4 本地差分隐私下的小批量梯度下降

本节主要研究构建满足

ε

-本地差分隐私下的经验风险最小化的机器学习模型，使用梯度下降法实现

.

参照Nguyên等人的对比实验结果，使用小批量梯度下降可以得到比随机梯度下降法更为准确的结果，所以论文使用小批量梯度下降法实现经验风险最小化

.

构建了满足本地差分隐私的小批量梯度下降法之后，使用其完成线性回归任务来验证该框架性能

.

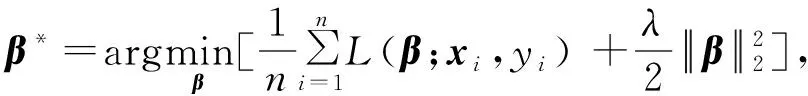
(15)

其中

λ

为正则化因子

.

在本文中，主要考虑线性回归的损失函数，损失函数如式(16)所示：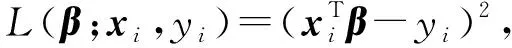

(16)

在机器学习中，获得的最普遍的计算方式是使用随机梯度下降法

.

使用该方法时，首先初始化一组向量，然后进行迭代更新，得到新的向量,,…,使用式(17)实现迭代更新：+1=-

γ

×∇(;,),

(17)

与非隐私状态下不同的是，在本地差分隐私的条件下，∇不会被用户端直接发送给聚合器，而是以隐私的方式进行收集

.

基于这个原因，已有的工作提出聚合器可以在每次迭代中收集用户加噪之后的∇

.

因为每次迭代中的梯度都是数值型数据，所以可以使用针对数值型数据的本地差分隐私扰动方法来对梯度进行扰动，本文使用算法3对梯度进行扰动

.

考虑到本地差分隐私中的隐私分配问题，如果使用随机梯度下降进行计算的话会导致加入的噪声过多，从而导致结果偏差较大，准确性较低

.

所以，这里使用的是小批量梯度下降法

.

也就是说，在每一次迭代中，随机选取一组用户

G

，

G

中每一个用户都提交扰动后的梯度给服务器，服务器再将梯度更新为这组用户提交的梯度的均值，式(18)给出了梯度更新的公式：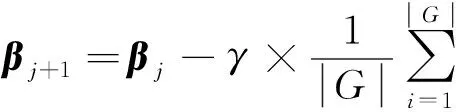

(18)

5 实 验

为了更好地评估论文中提出的方法的性能，论文使用了多种真实数据以及合成数据对该方法进行实验.

对于真实数据，使用了：1)从Integrated Public Use Microdata Series抽取的2个公共数据集，BR和MX，它们分别是巴西和墨西哥的人口普查记录.BR包含了16种属性，其中6种为数值型属性，10种为分类型属性.MX则包含19种属性，分别为5种数值型属性以及14种分类型属性.2)人类活动识别数据集WISDM,这是来自35名参与者在安卓手机上的加速度计数数据，将其中的时间戳一列数据删除，剩下包含3种数值型数据以及2种分类型属性在内的5种属性.3)抽取了ADULT数据集中属性Age一列.将这4种真实数据集的数值型属性域都规范到[-1,1].

除了真实数据集之外，论文还使用了合成数据集，分别是：1)服从高斯分布的GAUSS数据集，其中设置数据均值为0，标准差为0.25. 2)服从指数分布的EXP数据集，将标准差设置为0.5. 3)服从均匀分布的UNIFORM数据集.在均值估计实验中，为了消除误差影响，每种方法重复运行了100次取其平均值.

5.1 参数α的影响

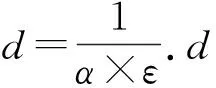
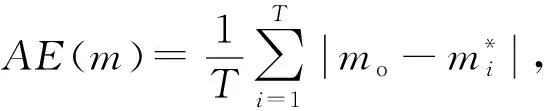
(19)

其中,

T

代表运行的次数，

m

代表真实的均值，

m

*代表均值的估计值

.

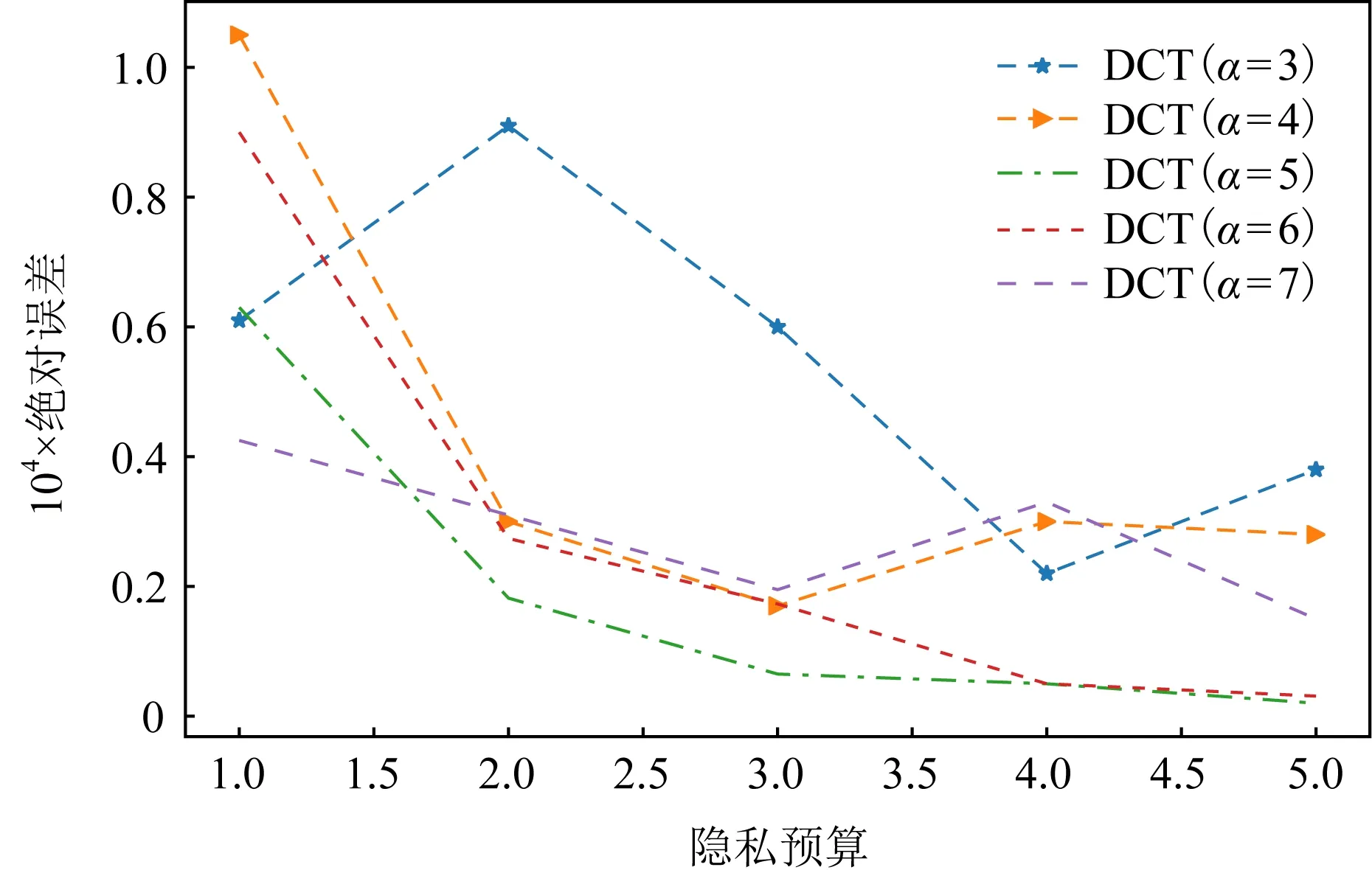
Fig. 1 The influence of different α on the mean estimation图1 不同α值对均值估计的影响

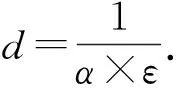
5.2 不同数据集的AE值对比

为评估分类变换扰动机制的性能，论文计算不同机制扰动后均值估计的绝对误差进行对比.每个用户对本地数据进行扰动，服务器收集用户扰动后的数据之后计算数值属性的均值.除了使用论文中提出的机制，还使用了已有的较新的扰动方法来进行比较，包括Wang等人提出的方法PM(如算法2所示)和Duchi等人的方法(如算法1所示)，这也是目前连续数值型数据扰动比较有代表性的方法.为了使结果更加的真实可靠，论文在1个真实数据ADULT和3个合成数据上进行了实验.

由图2中不同类型数据集中的实验结果可看出，绝对误差随着隐私预算的增大而减少.由于Duchi方法的最坏情况下误差方差在隐私预算较小时与PM接近，所以当隐私预算小于1时，Duchi和PM方法的结果较为接近.而论文中提出的分类变换扰动机制的绝对误差则要比这2种方法的误差小的多，不管隐私预算如何变换，该机制的绝对误差比其他2种方法要小几乎1个数量级.也就是说，论文中提出的方法在均值估计中的准确性得到了明显的改善.

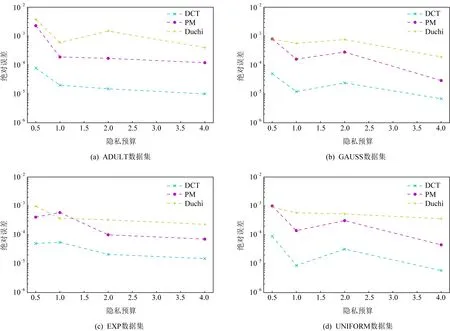
Fig. 2 The mean estimate of different datasets图2 不同数据集的均值估计

5.3 数据量的影响

在统计任务分析中，数据量的大小通常会影响最终结果的准确性，这里将论文中提出的机制与现有机制的性能受数据集大小影响进行对比.为更好地对比数据量变化对算法性能影响，使用不同大小的高斯数据集进行均值估计，最后比较其绝对误差的值.从图3的实验结果可以看出，绝对误差随着数据集的增大呈下降趋势，也就是说数据量越大结果往往越准确.PM方法的绝对误差和Duchi方法的比较接近，而分类变换扰动机制的误差始终要比PM方法以及Duchi方法的要更小.在不同的数据集大小中，分类变换扰动机制均体现出更好的性能，这主要是因为该机制使用了数据变换的方法，使得扰动满足本地差分隐私的同时数据能获得更高的准确性.

Fig. 3 The impact of dataset size图3 数据集大小的影响

5.4 经验风险最小化

在经验风险最小化实验中，采用小批量梯度下降算法完成线性回归的学习任务，将用户无放回的进行分组，同时为降低迭代过程中的噪声，将训练轮数设置为训练集长度除以每组人数的向下取整的值，使得用户最多参与1次训练.对于数据集BR和MX，将“totalincome”数值属性作为因变量，其他所有属性作为自变量.对于WISDM数据集，将最后1个数值属性作为因变量，其他所有属性作为自变量.对于数据集中的分类属性，其处理方式与文献[8]中的方法一样.将每个具有

k

种值的分类型属性

A

转换成

k

-1元属性，每一个属性的值域为{0,1}，使得：1)

A

中的值如为第

i

个值(

i

<

k

)则第

i

元属性会被设置为1，其余的

k

-2个属性会被设置为0

.

2)

A

中的值如为第

k

个值则其转换的属性所有的值都为0

.

转换之后，BR的维度为90，MX的维度为94，WISDM的维度为43.论文中使用的是小批量梯度下降算法，每一次迭代中抽取1组用户，该组中的用户对梯度进行扰动.用户将扰动后的梯度发送给服务器，服务器根据接收到的用户的梯度进行梯度更新后返回给用户.该实验包含了3种方法：DCT，PM，Duchi.对于所有的方法，都将正则化因子设置为

λ

=10.对于每一个数据集，使用5折交叉验证5次来评估每种方法的性能.使用均方误差(mean square error,

MSE

)比较使用不同扰动机制构建的小批量梯度下降算法的优劣.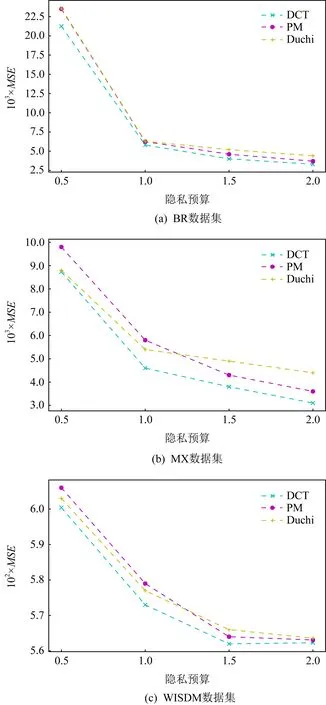

Fig. 4 Linear regression using different perturbation mechanisms图4 使用不同扰动机制的线性回归

图4描述了在不同的隐私预算下，每一种机制在不同数据下的线性回归模型的均方误差.可从实验结果看出，PM方法和Duchi方法构建的满足本地差分隐私的小批量梯度下降模型的训练效果更为接近，论文中提出的分类变换扰动机制计算出的均方误差要小于这2种机制，获得的模型准确度更高，性能要更优.总的来说，所有实验结果表明，不管是在均值估计中还是在经验风险最小化的任务中，分类扰动机制的性能都要优于现有的本地差分隐私的解决方法，其在简单和复杂的数据分析任务中均能获得较高的准确性.

6 结 论

为了防止用户隐私泄露，论文提出了满足本地差分隐私的分类变换扰动机制.该机制将数值型数据的扰动与分类型数据的扰动进行结合，提高了均值估计的准确性.同时，将该机制用于梯度下降中的每次迭代的梯度扰动，保护了训练过程中用户隐私的同时得到了一个较为准确的模型.而且，本文也从本地差分隐私定义的角度，理论证明了提出的方法满足ε-本地差分隐私.最后通过多组真实数据集以及合成数据集验证了分类变换扰动机制的性能，证明了其在相同条件下要优于现有的同类方法.下一步工作将研究如何在更为复杂的数据分析中实现隐私保护并提高准确性.

作者贡献声明

：朱素霞对研究思路提供指导意见，协助设计论文框架，并对论文初稿、修改稿等提供审阅意见；王蕾提出研究思路,设计研究方案,进行实验和数据分析,并撰写论文;孙广路对研究思路提供指导意见，并对论文初稿、修改稿等提供审阅意见.