双重路由深层胶囊网络的入侵检测系统
2022-02-11尹晟霖张兴兰左利宇
尹晟霖 张兴兰 左利宇
(北京工业大学信息学部 北京 100124)
随着信息时代的不断发展,互联网络已经深入到了社会的方方面面,正在改变着人们的生活、学习和工作方式,同时面临的各种安全威胁也在不断增加,提供对数据的保护是安全开发人员面临的重要挑战.入侵检测技术是一个维护网络安全的重要方式,其本质上是一个对网络流量进行分类的任务,即识别网络流量的行为是正常还是异常.传统机器学习技术已被广泛用于入侵检测系统中,虽然机器学习的算法在处理分类任务中有着不错的表现,但是大多数的机器学习算法只是浅层的学习,并不能很好地提取数据流量中的特征,缺乏良好的泛化能力,随着恶意攻击的不断变化,出现了许多挑战.深度学习有着较强的特征提取的能力,它可以将数据映射到更高维度上去提取分析特征,随着深度学习技术不断创新和发展,在语音识别、图像处理等领域获得了令人瞩目的成就,越来越多的人开始将深度学习与入侵检测相结合,以提升入侵检测系统的泛化能力.
近年来,循环神经网络(recurrent neural network, RNN)和卷积神经网络(convolutional neural network, CNN)已被运用到入侵检测当中,但这些方法仍然存在着一些问题.RNN一般被用来处理时间序列数据,下一时刻的信息会依赖于上一时刻的信息,在处理特征过程中,RNN会把每个位置上的特征融合到一起,并且随着序列的增加,会逐渐丢失前一段的信息.长短时记忆网络(long short-term memory, LSTM)解决了信息丢失的问题,但仍会融入每个位置上的信息.对于入侵检测数据,并不是每一个特征都会对分类结果起到有效的作用,融入过多非必要的特征会产生噪音,影响最终的分类结果.CNN被用来提取和处理图片中的特征,在有些工作中可以将入侵检测数据的特征数组重组,转化成图片数据格式,再通过CNN进行处理.但CNN模型在处理数据的过程中,难以表达特征位置关系复杂对象的特征,会降低模型的准确率.
为了解决这个问题,本文提出了基于胶囊网络的入侵检测技术,将胶囊网络运用到入侵检测的任务中,为了能够拟合不同分布的数据,本文使用深层胶囊网络来提取更深层的特征,通过双重路由机制来弥补单路由机制中不能很好拟合复杂分布的缺陷,并使用残差连接和胶囊丢弃机制来稳定动态路由过程,同时增添了一个噪音类来收集对分类结果起到负作用的特征以减少数据中的噪音,从而提高模型的准确率.最后模型在NSL-KDD数据集和CICIDS2017数据集上进行了测试,同时与多个模型进行对比,结果显示,本文的模型在2个数据集上都取得了不错的效果.
1 相关工作
1.1 基于深度学习的入侵检测
随着在机器学习基础上的大量研究,入侵检测技术得到了提升.但传统的机器学习技术在处理大数据流量时稍显吃力,越来越多的人尝试将深度学习技术与入侵检测技术相结合.
文献[2]将遗传算法和模拟退火算法运用到深度神经网络(deep neural network, DNN)中,将传统的机器学习算法与深度学习框架相结合,提出了基于机器学习的入侵检测系统(intrusion detection system based on machine learning, MLIDS).文献[3-5]分别提出了基于RNN、基于门控循环单元(gated recurrent units, GRU)和基于LSTM的入侵检测系统,将数据当作时间序列来处理.在NSL-KDD数据集上进行了实验,文献[6]在训练集上达到了99%的准确率,但因没有在测试集上进行验证,不具有代表性.文献[7]使用了CNN模型,在处理后的数据上进行1维卷积的操作,文献[8]则是将数据数组重组成类似于图片数据的矩阵的形式后进行2维的卷积操作,也是在NSL-KDD数据集上进行实验,都取得了不错的效果,但仍有许多提升的空间.文献[9]使用了孪生神经网络(siamese neural network, SNN)来处理入侵检测数据中类别不平衡的问题.此外,随着深度学习的不断发展,许多基于混合神经网络模型被逐渐运用到入侵检测上来.文献[10]使用了CNN与双向LSTM结合点方式,并使用了交叉验证的方式获得了效果最好的模型,取得了较高的准确率.文献[11]提出了一种基于LightGBM算法的入侵检测系统,极大减小了数据的计算量,并取得了不错的效果.
1.2 胶囊网络
Hinton首次提出了胶囊网络的概念,在文献[12]中运用在了图像分类的任务中,并在文献[13]中得到了改进.文献[14-15]将胶囊网络运用到了文本分类任务中,文献[16]则运用到了目标识别场景下.由此可见,胶囊网络在深度学习中是一个很有前途的概念,但到目前为止,其真正的潜能尚未得到充分的发挥,该模型被认为可能成为下一代重要的神经网络模型.胶囊网络是由胶囊(capsule)组成的,胶囊是一组神经元的集合,与传统的神经网络不同,在胶囊中,神经元的集合是向量或者矩阵.基于矢量的表示能够抓取更多的特征信息并能够在学习过程中对输入特征组之间的潜在相互依存关系进行编码,同时引入动态路由迭代过程,通过聚类的方式对特征进行归类,利用该耦合系数来测量预测上层胶囊和下层胶囊的向量之间的相似度,并将下层胶囊指向特定的上层胶囊.通过这个过程,胶囊学会了代表给定实体的属性,这是一种更加有效的特征编码方式,改善了RNN和CNN的缺陷.
2 基于残差的双重路由胶囊网络

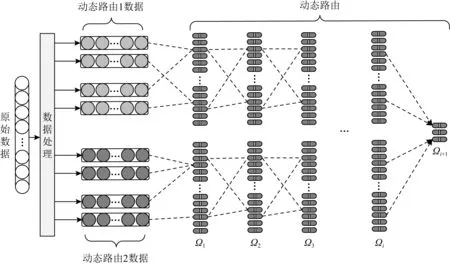
Fig. 1 Double routing capsule network with residuals图1 残差的双重路由胶囊网络
2.1 数据处理模块

利用注意力机制可以更加精确地捕捉更相关的特征,传统的注意力机制过度地关注了Token之间的联系,减少了模型的泛化能力,并增加了运行过程中的参数.为了减少模型参数并提升泛化能力,本文使用的是混合注意力机制,它在文献[17]中被证明是有效的.混合注意力机制是由2种不同的注意力机制叠加形成的,结构如图2所示.

Fig. 2 Mixed attention mechanism图2 混合注意力机制

F
(+)+,(1)




(2)

(3)
最后将得到的2个注意力矩阵混合,即

(4)

2.2 动态路由模块
在动态路由机制模块中,在获得处理后的低级胶囊的输出后,要确定高级胶囊中哪个被激活,低级胶囊如何分配到高级胶囊中.本文使用了2种路由方式来完成特征的聚类过程,分别是K
-Means算法的动态路由和EM算法的动态路由.2.2.1K
-Means算法K
-Means算法是一种无监督的聚类算法,通过初始化聚类中心,经过多次迭代后将样本点进行聚类.在动态路由算法中,将流量数据的特征视为样本点,对特征进行聚类.将低级胶囊中的特征聚类为高级胶囊,K
-Means算法是一种行之有效的聚类方法.它希望将已有的数据特征(,,…,)无监督的划分为k
个类,使得产生的k
个聚类中心(,,…,)之间的间隔最小:
(5)
将Ω
层胶囊和Ω
+1层胶囊之间的动态路由看作是一个K
-Means聚类的过程,则Ω
+1层胶囊是Ω
层胶囊的聚类中心,式(5)中的d
为相似程度的度量.
使用数据处理层输出的数据=(,,…,)来初始化,迭代公式为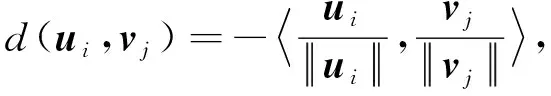
(6)
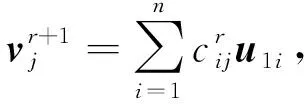
(7)

(8)

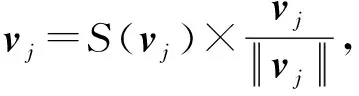
(9)

(10)

Fig. 3 Vanilla Squash function图3 原始压缩函数图像
注意到函数S
()能够将向量的模长压缩到[0,1]之间,它存在着多种方式.
文献[10]中的函数对全局进行了压缩,对于自变量细微的变化不敏感,容易丢失许多信息.
本文对函数S
()进行了修改,使用了3种不同形式的激活函数,公式为
(11)

(12)

(13)
3种激活函数的图像如图4所示,改进后的激活函数放大了自变量为0附近的值时,函数值对自变量的变化更加敏感,可以使各类之间的间距变大,从而产生更大的类分离.
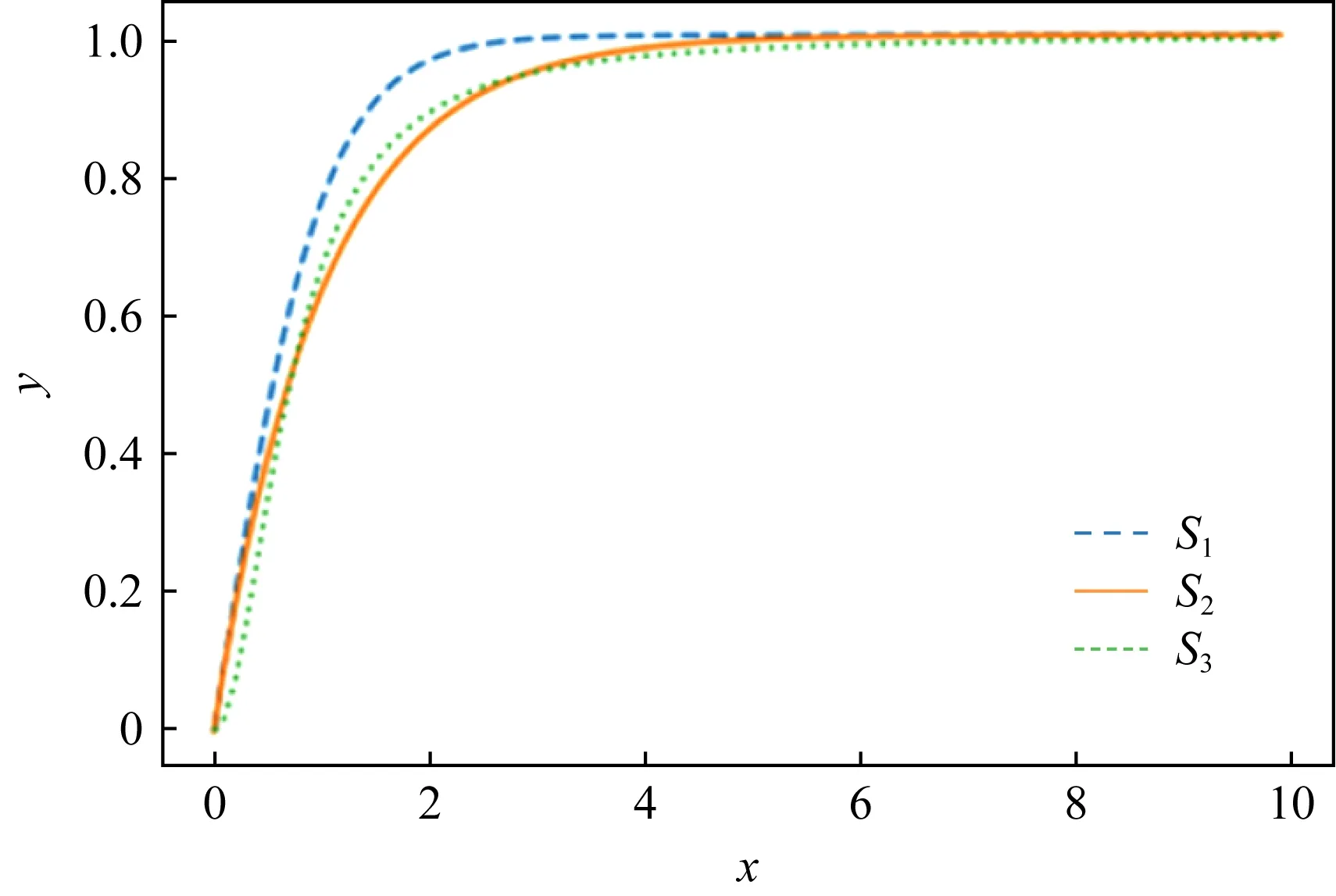
Fig. 4 Three Squash functions图4 3种压缩函数图像
本文使用以上3种激活函数进行了实验,实验结果表明,S
()的效果要优于另外2种.
整个迭代过程的路由算法如下:
算法1.
K
-Means路由算法.
输入:;输出:Squash
().

i
to高级胶囊j
迭代r
次

⑤ end for
⑥ 返回Squash
().
2.
2.
2 EM算法在EM(expectation-maximum)算法中,Ω
+1层胶囊被看作高斯混合分布,而Ω
层胶囊的输出从到需要被聚类的数据点.
通过在E
_Step
和M
_Step
之间交替迭代地更新输出胶囊的均值、方差,以及输入胶囊的分配概率R.
动态路由机制也可以被看作一个反向的注意力机制过程,通过全局的特征,动态地调整局部特征的贡献程度.
经过处理的数据符合混合高斯分布,通过迭代以获得最大的分布函数p
(),低级胶囊中的特征值之间相互独立,因此协方差矩阵是一个对角矩阵.
对标准EM迭代算法改动后的分布函数公式为
(14)

(15)

(16)
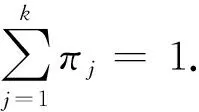
M
_Step
中,通过得到的分配概率求出迭代改进后的高斯混合模型(Gaussian mixture model, GMM)的参数.
该步骤是获得给定迭代的低级胶囊之间的总体表示.E
_Step
调整每个数据点到高斯分布的分配概率R
,即低级胶囊到高级胶囊之间的分配概率,该过程基于给定迭代的高级胶囊来调整每个胶囊的贡献.
GMM是基于加权的欧氏距离,其特点是聚类中心向量是类向量的加权平均,因此不能使用向量的模长来表示特征的显著程度.为了解决这个问题,使用一个标量a
对最后的结果进行缩放,缩放之后便可通过压缩函数来计算向量的模长.通过EM算法得到的是一个概率分布来描述一个类.这个类的不确定性越大,方差就越大,代表着越接近均匀分布,说明特征不够突出,此时a
的值应该越小;若不确定性越小,方差就越小,此时的分布就越集中,a
的值则会越大.
此过程使用不确定性来描述a.
将p
(x
|j
)带入信息熵公式化简可得S
:
(17)


(18)
其中,r
为随机初始化的标量,范围在(0,1]之间.
因为显著程度越大,信息熵越小,所以本文用-S
来衡量特征的显著程度.
同时为了将S
的大小限制在[0,1],使用Sigmoid函数来对S
进行变化:a
=Sigmoid(1-S
).
(19)
得到缩放尺度后,仍然使用压缩函数将向量压缩到[0,1]之间来表示特征的显著程度,新的压缩函数NSquash
为
(20)
整个迭代过程的路由算法如下:
算法2.
EM路由算法.输入:;输出:NSquash
(a
,).
① 初始化参数:a
,V
,σ
;② for迭代r
次③ ∀j
∈Ω
+1:M
_Step
(a
,R
,V
,j
);④ ∀i
∈Ω
:E
_Step
(μ
,σ
,V
,i
);⑤ end for
⑥ 返回NSquash
(a
,).
E
_Step
(μ
,σ
,a
,V
,i
)

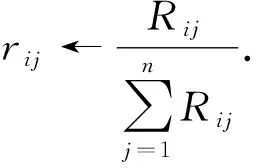
M
_Step
(a
,R
,V
,j
)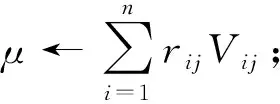
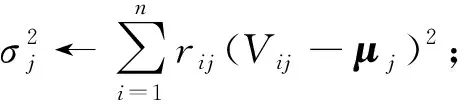

a
←Sigmoid(1-S
).
2.2.3 深度胶囊与残差连接
网络层数越深,越能提取到丰富的特征.但简单地通过堆叠胶囊层来构建深层胶囊网络会与传统的MLP模型相似,出现梯度弥散或者梯度爆炸的现象,即便使用正则化来处理,也会在训练集上出现网络退化的现象.此外,胶囊网络的动态路由机制是一个非常昂贵的计算过程,多个胶囊层的叠加会导致训练的时间增加.现有的研究表明,单纯将胶囊层叠加在一起会导致中间层的学习效果有所下降.这是由于当胶囊数量过多时,胶囊之间的耦合系数会过小,从而抑制了胶囊网络的学习,导致学习效果下降.为了解决这一问题,本文改进了原有的动态路由机制.
首先,为了避免在路由过程中胶囊数量过多,本文采用了Dropout层的思想,对胶囊进行失活,丢弃某个胶囊.但在这个过程中不采用随机失活的方式,因为随机失活很有可能会导致含有重要特征的胶囊丢失,影响模型的性能.在失活过程中,会对贡献度低的胶囊进行丢弃,若每个胶囊的贡献度一样,则本迭代不删除任何胶囊.从低层胶囊Ω
到达下一层胶囊Ω
+1之后,在K
-Means动态路由中,删除长度较小的胶囊;在EM动态路由中,删除显著程度a
较低的胶囊.过程如图5所示,含有阴影的胶囊为丢弃的胶囊: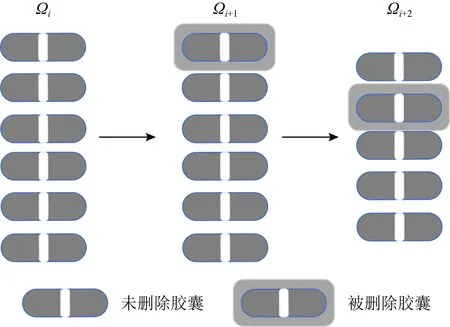
Fig. 5 Capsule network Dropout mechanism图5 胶囊网络Dropout机制
其次,在聚类迭代过程中,由于浅层胶囊用来捕获低级特征,深层胶囊用来捕捉高级特征,所以浅层胶囊之间使用较小的迭代次数,设i
=1;中间层胶囊设i
=2;深层胶囊之间使用正常的迭代次数,设i
=3.
同时,动态路由的胶囊过程中,随着胶囊层数的增加,会出现模型过拟合以及网络退化的现象.
为了使模型能够得到收敛同时有保证不会出现过拟合以及退化的现象,也使用残差连接来解决这个问题.
残差连接过程如图6所示.
残差公式为+2=+2+,(21)
是可学习的参数矩阵,是j
层的胶囊的结果,+2是j
+2层胶囊的结果.
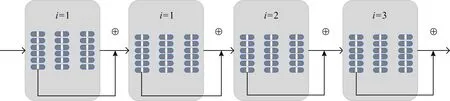
Fig. 6 Skip connection图6 跳跃连接
2.
2.
4 噪音胶囊胶囊网络会提取样本中的所有特征,因此本文通过增加一个不属于之前类别的噪音胶囊来收集胶囊网络提取到的噪音特征,以提高模型的准确性,最终分类胶囊中含有c
+1个胶囊,c
为样本数据集中的类别数目.
2.3 训练目标
本文使用的是边缘损失函数和重构损失,训练目标使得2个损失函数之和的值最小.
边缘损失函数是基于分类层输出的向量长度的分类损失,公式为
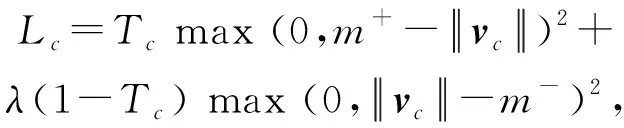
(22)

重构损失是计算原始数据与重构数据之间的差距,使用均方误差来计算实现,公式为
L
=λ
∑MSELoss
(Data
,Data
),(23)
其中,Data
为原始的数据,Data
为重构后的数据,λ
为重构损失缩放倍数,缩放倍数越大,越会导致模型的过拟合.
整个模型优化的整体损失为
L
=L
+L
.
(24)
3 实验及分析
3.1 数据集与数据处理
本文采用的是NSL-KDD数据集和CICIDS 2017数据集.
NSL-KDD是KDD CUP99数据集的改进版,删除了原始KDD数据集中的冗余数据,在测试集中没有重复的记录,并且有着合理的数据量.数据集中含有4种异常类型,被细分为39种攻击类型,其中有17种未知攻击类型出现在测试集中.每一条记录包括41个特征和1个类别标识.其中41个特征中是由TCP连接基本特征(9种)、TCP连接内容特征(13种)、基于时间的网络流量统计特征(9种)和基于主机的网络流量统计特征(10种)组成.
CICIDS2017数据集包含最新的常见攻击,更接近于真实的数据.完整的CICIDS2017数据集包含八个文件,总共含有3 119 345条实例和83个特征,其中包含15个类别标签(1个正常标签,14个攻击标签).此外,数据集中含有288 602个标签缺失的实例和203个特征缺失的实例.删除缺失信息的实例后,总共得到2 830 540个实例.
数据集中标签分布如表1和表2所示:

Table 1 Number of Categories in NSL-KDD Dataset表1 NSL-KDD数据集中各类别的数量

Table 2 Number of Categories in CICIDS2017 Dataset表2 CICIDS2017数据集中各类别的数量
数据处理包括字符类型数字化、类别不平衡处理、归一化处理3个步骤.
1) 字符类型数字化
在数据集的特征中,有3个特征和类别标识是字符类型的.在字符类型数字化的过程中,使用了one-hot方式.对于NSL-KDD数据集,协议类型的值有3种,目标主机的网络服务类型有70种,连接正常或者错误的状态有11种.在one-hot方式下,协议类型被处理为[1,0,0],[0,1,0],[0,0,1]的形式,其他特征处理过程类似,最终每条数据的长度为121维.CICIDS2017数据集处理的过程同上.
本文在实验过程中使用了one-hot编码的方式,以NSL-KDD数据集为例,将数据处理成长度为121的向量,为了实现可视化,将特征长度121维的数据转化为11×11的矩阵,图7展示了Normal,DoS,Prob这3种标签的图像,可以看出,每种类别之间,都包含着相似的特征分布.

Fig. 7 Partial sample visualization of the NSL-KDD dataset图7 NSL-KDD数据集部分样本可视化
2) 类别不平衡处理

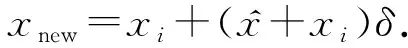
(25)
但是SMOTE算法的缺点是生成的少数类样本容易与周围的多数类样本产生重叠难以分类,会影响分类器的效率,而数据清洗技术可以处理掉重叠样本,通过使用ENN(edited nearest neighborhood)算法,将与多类样本重叠的数据删除.
对于NSL-KDD数据集,直接使用SMOTE+ENN算法处理数据,生成新的训练集与测试集.对于CICIDS2017数据集,先将同性质的标签进行合并,再均匀地对每个标签下的数据进行筛选,避免处理后造成数据偏大.最后使用SMOTE+ENN算法进行处理.处理后的数据集如表3和表4所示.
3) 归一化处理
为了消除不同量纲带来的数据差异,在对字符变量数字化以后,进行归一化处理.采用最大最小归一化的方法,可以减轻由于量纲不同造成的差异,将数值统一在[0,1]之间,公式为

Table 3 Processed NSL-KDD Dataset表3 处理后的NSL-KDD数据集

Table 4 Processed CICIDS2017 Dataset表4 处理后的CICIDS2017数据集
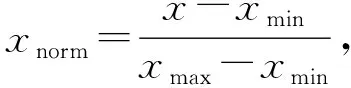
(26)
其中,x
是原始数据,x
是同一特征中的最小值,x
是同一特征中的最大值,x
是原始数据归一化后的结果.
数据处理完成后,对于NSL-KDD数据集,使用新生成的训练集和测试集进行模型的训练和测试;对于CICIDS2017数据集,使用全体数据集的70%进行训练,30%用于测试,其中训练集中不包含测试集中的数据.
3.2 实验结果及分析
本文使用准确率AC
、精确率P
、召回率R
、F
1作为实验结果的评价指标,其中TN
(true negative)是负样本且被判为负样本的数量,TP
(true positive)是数据为正样本且也被判为正样本的数量,FN
(false negative)是数据为正样本但被判为负样本的数量,FP
(false positive)是数据为负样本,但被判为正样本的数量.
(27)
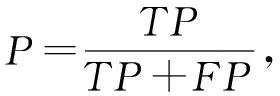
(28)

(29)

(30)
1) 在NSL-KDD数据集上实验
在实验过程中,将训练集划分为5等份进行5折交叉验证,使用了机器学习算法随机森林(random forest, RF)、决策树(decision tree, DT)和神经网络算法ResNet-50(residual network)、BiLSTM(bi-directionallong short-term memory)、原胶囊网络(vanilla capsule)作为对照模型,实验结果如表5所示:

Table 5 NSL-KDD Dataset Results表5 NSL-KDD数据集结果
从结果可知,混合路由机制胶囊网络的泛化能力要高于机器学习算法和传统神经网络,本文模型在准确率上比机器学习算法DT高2个百分点,比ResNet50深度网络高5.2个百分点,比原胶囊网络高2.24个百分点.
虽然每个类别有自己独特的特征分布,但是不同种类之间也包含着相似的特征点.传统的神经网络,如CNN擅长对特征的检测与提取,它可以很好地检测出不同类别所含有的特征.但是它在探索特征之间的空间关系方面效果不佳.如图8所示.

Fig. 8 Sample visual comparison图8 样本可视化对比
两者都包含相似的特征点,对于传统的神经网络,非常容易将异常数据识别为正常数据,或者将正常数据识别为异常数据,导致分类器精度降低.这是因为传统神经网络具有平移不变性,而胶囊网络会捕捉特征之间的空间关系,从而提升分类模型的泛华能力.
NSL-KDD数据集仍存在着一些问题,其测试集中含有训练集从未出现过的种类以及特征分布,训练集和测试集的分布有一定的差异,导致模型准确率有所下降,所以NSL-KDD数据集不太适用于检验模型的性能.
2) 在CICIDS2017数据集上实验
本文使用CICIDS2017数据集对模型进行了进一步探究.实验过程与在NSL-KDD数据集上一致.实验结果如表6所示:
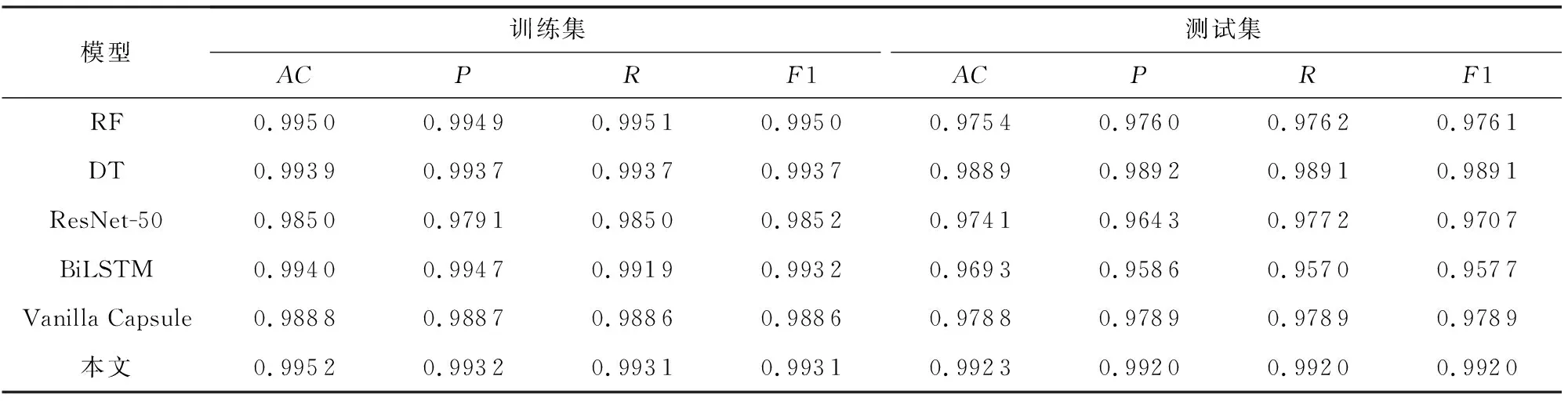
Table 6 CICIDS2017 Dataset Results表6 CICIDS2017数据集结果
由实验结果可知,本文的准确率比RF高了1.69个百分点,比BiLSTM高了2.3个百分点,效果有了明显的提升.
本文对提出的3种不同的激活函数S
(式(11)),S
(式(12)),S
(式(13))与原始激活函数Vanilla进行了对比实验,实验结果以及收敛过程如表7和图9所示.由实验结果可得,使用S
有着更好的泛化能力以及更快的收敛速度,且趋于稳定.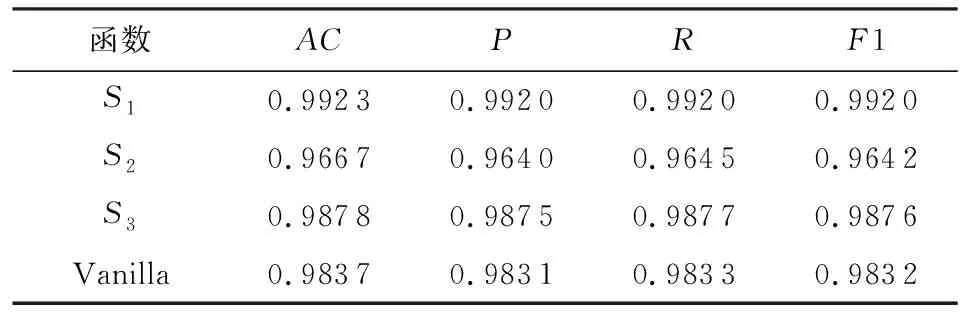
Table 7 Results of Different Activation Functions表7 不同激活函数结果
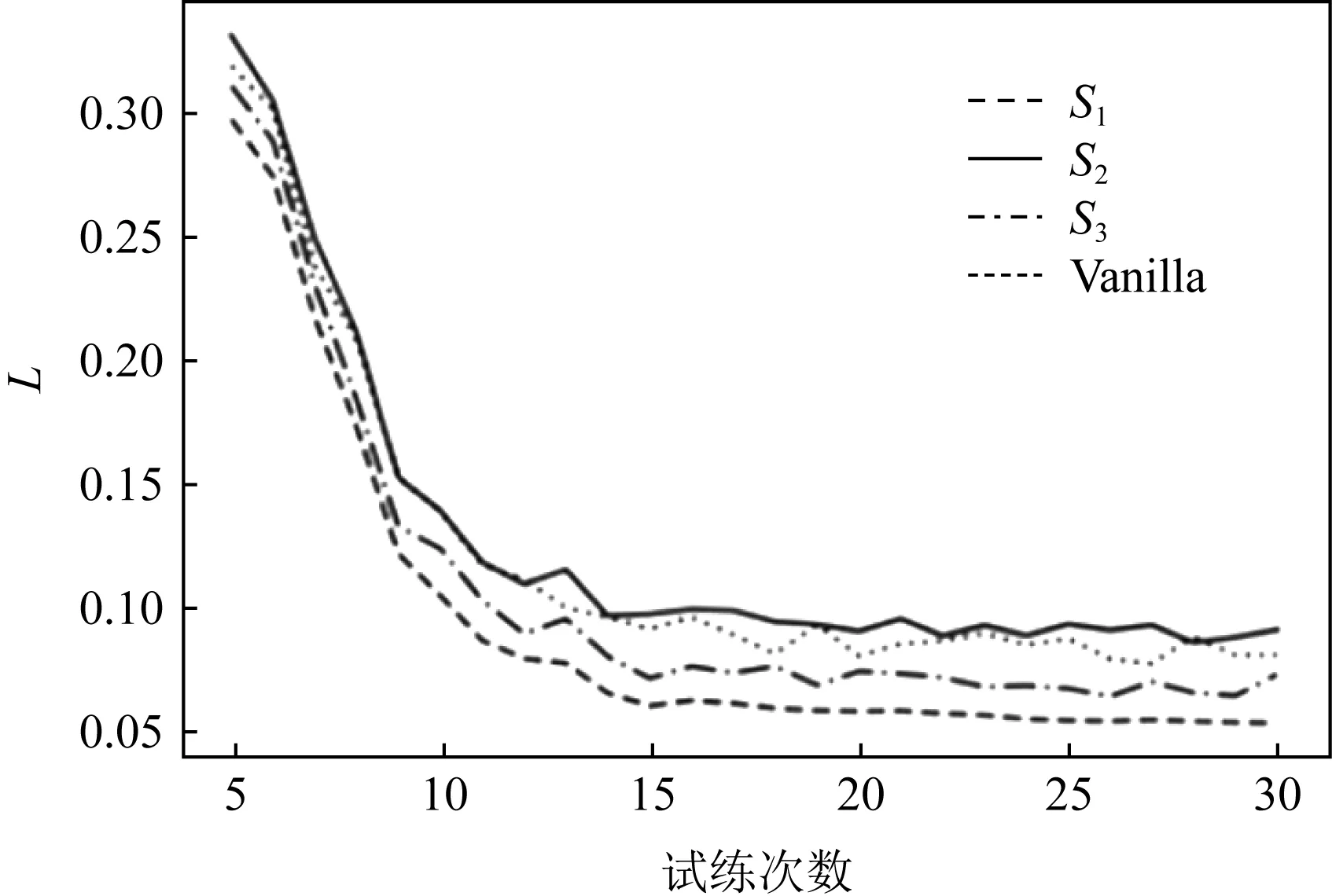
Fig. 9 Relationship between L and training times图9 L与训练次数关系
为了验证残差连接的有效性,本文将有残差连接模型(本文)与没有残差连接的模型(CapsuleA
)进行了对比,准确率如表8所示:
Table 8 Comparison Results with the Non-residual Model表8 与无残差连接模型对比结果
由此可见,经过检验,不含残差连接的模型在训练集上和测试集上,准确率都有所下降,说明网络加深以导致了模型出现了网络退化以及过拟合现象,并且所损耗的时间大大增加.通过残差连接可以很好地解决模型过拟合以及网络退化的问题,并提高运行效率.
3) 模型效率分析
为了研究模型在推断阶段的效率,本文比较了传统机器学习算法与神经网络算法运行一个Batch所需要的时间.其中CapsuleB
模型只是单纯加深了网络深度,网络层数与本文提出的模型一致,且CapsuleB
模型在NSL-KDD数据集上的准确率为83.78%.实验结果如表9所示:
Table 9 Results ofthe Models’ runtime表9 模型运行时间结果 s
由实验结果可知,本文的运行时间要小于单纯的将胶囊层数叠加的模型(CapsuleB
),且单纯的叠加胶囊层数并没有达到较好的效果.同时,神经网络算法的运行时间普遍大于传统机器学习的算法.在实际应用中,本文算法的时间消耗仍在可接受的范围内,与ResNet网络相当.随着数据的爆发式增长,传统的机器学习算法将不再适用,而神经网络算法随着数据的增加,在一定程度上可以有效地提升模型的准确度,且深度神经网络算法可以很好地在GPU上得到加速,随着设备的发展,时间效率问题可以进一步得到缓解.4 结束语
本文构建了双重路由机制的胶囊网络模型,通过使用不同的动态路由算法进行相互补充,根据数据集自动分配2种路由机制所占的比重,可以更好地拟合不同种类样本所形成的特征分布.同时,在特征提取过程中使用了混合注意力机制,使得模型更加关注对判别产生影响的特征,减少了噪音的干扰,增强了模型的鲁棒性.但在胶囊网络的动态路由机制过程中损耗时间要大于传统神经网络,今后需要通过进一步优化动态路由机制,提升胶囊网络模型的运行效率.
作者贡献声明
:尹晟霖提出了方法、完成实验以及撰写原稿;张兴兰负责整体监督与论文的修改;左利宇负责部分实验的实现以及实验结果的整理.
