拉索-惯质阻尼器体系减振分析 *

刘 菁,梁 栋,2

(1. 河北工业大学 土木与交通学院，天津 300401； 2. 河北工业大学 河北省土木工程技术研究中心，天津 300401)

0 引 言

拉索作为斜拉桥重要的受力构件，具有柔度大、单位长度质量轻且固有阻尼小(通常约为临界阻尼的1%)[1]的特点，但也容易出现涡激共振、参数共振[2]、尾流驰振、抖振和风雨激振等振动问题[3]。为抑制拉索振动，大跨度斜拉桥会采取各种拉索减振措施，其中附加外置机械阻尼措施可以直接增加拉索的模态阻尼比，是拉索减振措施中最为常用的方法[4]。但附加外置机械阻尼仅能使拉索某一阶振动模态获得最优模态阻尼比，且安装位置一般不超过索长5%，极大限制了黏滞阻尼器的减振效果[5]。

在研究主动、半主动阻尼器的过程中，人们发现负刚度可使阻尼器以更大位移运动，消耗更多能量并实现更大的阻尼比[6-7]。随着力学放大机制(如滚珠丝杠、齿轮齿条、杠杆摆，以及利用流体惯性的惯性泵等)的应用，动力质量可以提供较大的表观质量，相应的惯性力所体现的负刚度效应也逐渐用于结构振动控制。

在拉索减振方面，I.F.LAZAR等[8]将调谐质量阻尼器中的质量部分替换成惯质器，得到了调谐惯质阻尼器(TID)，针对拉索第一阶振动的减振分析表明，当安装高度相同时，TID可使拉索获得比传统黏滞阻尼器更高的模态阻尼比;L.SUN等[9]将被动负刚度装置应用于拉索附加阻尼器系统，以克服由于阻尼器安装位置限制而引起的附加阻尼不足问题，并讨论了由于负刚度引起的控制力非线性对系统分析的影响；J.LUO等[10]利用有限元方法，研究了3种惯质器应用于张紧弦的临界阻尼比，认为将惯质器应用于拉索减振可获得较好的减振效果；X.SHI等[11]提出了由提供负刚度的弹簧和油阻尼器合成的负刚度阻尼器，数值分析和试验验证了该阻尼器对拉索第一阶振型的减振性能远优于传统黏性阻尼器；L.LU等[12]采用数值方法分析了黏滞惯性质量阻尼器对拉索的减振效果，拉索第一阶振动的最大阻尼比达到了传统黏滞阻尼器的9倍，当安装位置降低至距索梁交点处的2%索长时，依然表现出了良好的减振效果；莫凯程[13]对利用滚珠丝杠惯性质量阻尼器抑制拉索振动进行了数值仿真和试验验证，研究认为，最优参数不同的惯性质量阻尼器，可以大幅提高斜拉索指定阶次的模态阻尼比；崔智鑫[14]用数值方法，讨论了3种构型的调谐惯质类阻尼器对拉索第一阶振动的减振性能，指出并联装置优于串联。

目前，利用惯性质量对拉索进行减振的研究还处于起步阶段，大多只开展了理论研究，至于如何在实际拉索减振中实现惯质减振，还需要开展更加多样化的惯质系统研究。为方便实现惯质，笔者设计了包括齿轮齿条、惯质元件和黏滞阻尼元件在内的实索用惯质阻尼器。齿轮齿条作为放大机构能够承受较大的振动荷载，且制作方便，易于实际工程应用。

1 齿轮齿条和黏滞阻尼组合的拉索惯质阻尼器

笔者采用的惯质阻尼器，其使用齿条和齿轮能通过一定齿比组合成为一种力放大的机械结构，将物理质量较小的旋转飞轮等效为一个虚拟的、具有较大惯性质量的质量块。其质量比调谐质量阻尼器(TMD)小得多，安装也相对方便，机械结构如图1。笔者设计的惯质阻尼器由惯质元件和黏性阻尼元件两部分组成，该阻尼器对加工精度要求不高，且能承受较大的拉索振动荷载。

在运动方式上，拉索与齿条间使用球铰连接，使拉索的面内、面外振动均能转化为齿条的上下振动。拉索振动使齿条进行直线往复运动，齿轮将齿条的直线往复运动转化为惯质圆盘旋转运动，同时带动黏滞阻尼元件叶片在阻尼液中做旋转运动，实现惯质元件和黏滞阻尼元件减振。

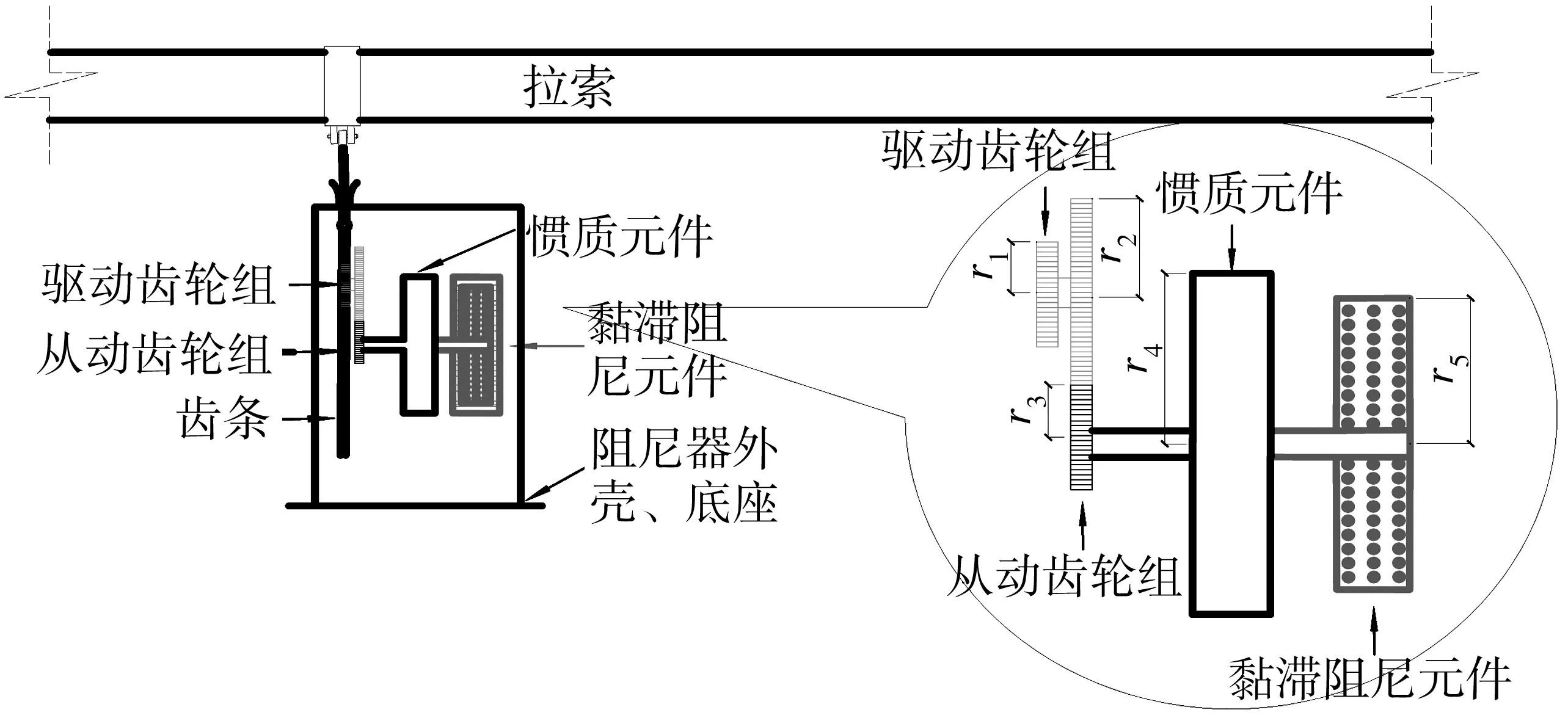
图1 拉索-惯质阻尼器装配示意Fig. 1 Assembly diagram of cable-inertial damper

2 惯质阻尼器的单体计算模型

惯质阻尼器的计算模型如图2，由惯质元件和黏滞阻尼元件两部分组成。惯质元件和黏性阻尼元件有同样的振幅、速度和加速度，二者在计算模型上属于并联关系。

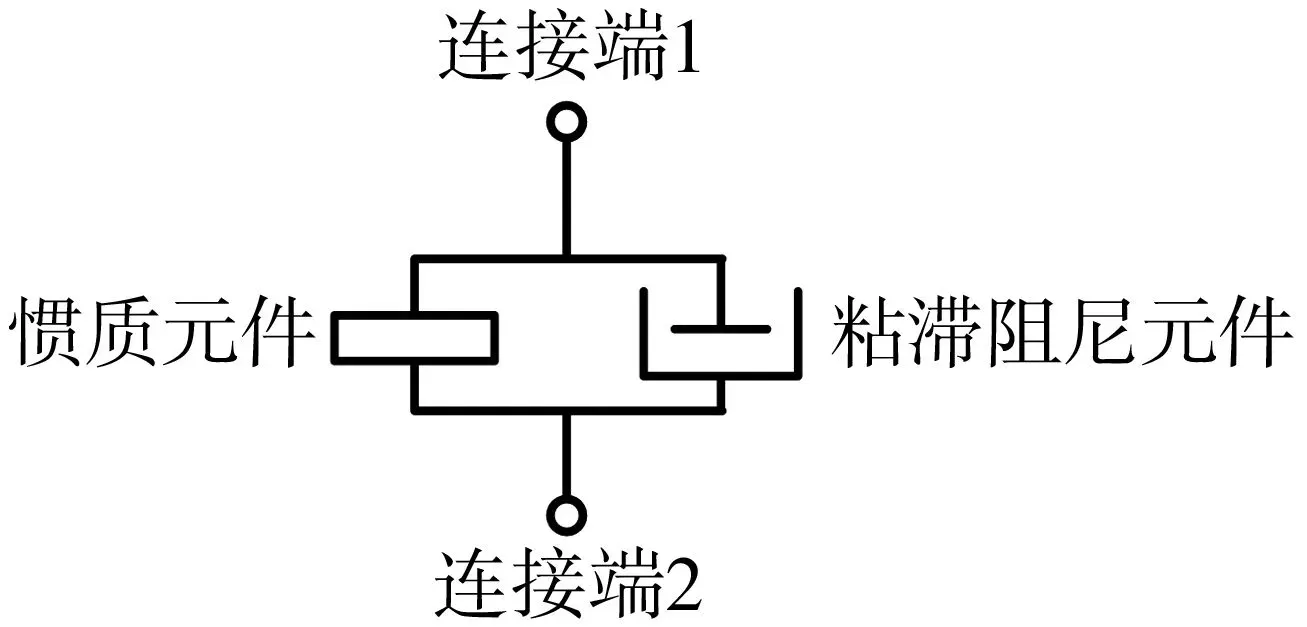
图2 惯质阻尼器单体计算模型Fig. 2 Calculation model of inertia damper

忽略各个传动部件间的转动阻力与传动齿轮的质量，阻尼器的阻尼力如式(1)：

(1)

式中：bd为惯质元件产生的惯质；cd为黏滞阻尼元件提供的阻尼系数；u为阻尼器两端之间的相对位移。在质量类阻尼器中，惯质的估算如式(2)：

(2)

(3)

式中：r1为驱动齿轮组小齿轮的半径；r2为驱动齿轮组大齿轮的半径；r3为从动齿轮的半径；r4为质量圆盘半径；r5为黏滞阻尼元件的叶片半径；ρ为惯质圆盘材料密度；h为惯质圆盘厚度；C为折算后阻尼液黏度系数。

将阻尼器的驱动齿轮、从动齿轮的半径设置为不同值，以实现不同质量放大效果。考虑阻尼器在外荷载作用下，阻尼力的计算由式(1)变为：

(4)

式中：设u=Asin(ωt)，A为简谐运动的幅值，ω为简谐运动的频率。

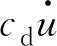
(5)

式中：ke为等效负刚度。

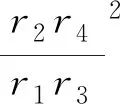
3 拉索-惯质阻尼器系统分析

为满足工程应用的需要，设计了的平面内斜拉索减振系统如图3。设在静平衡状态下的索力为T，拉索单位长度质量为m，索的总长为L，阻尼器在距离拉索桥面锚固端l1位置。

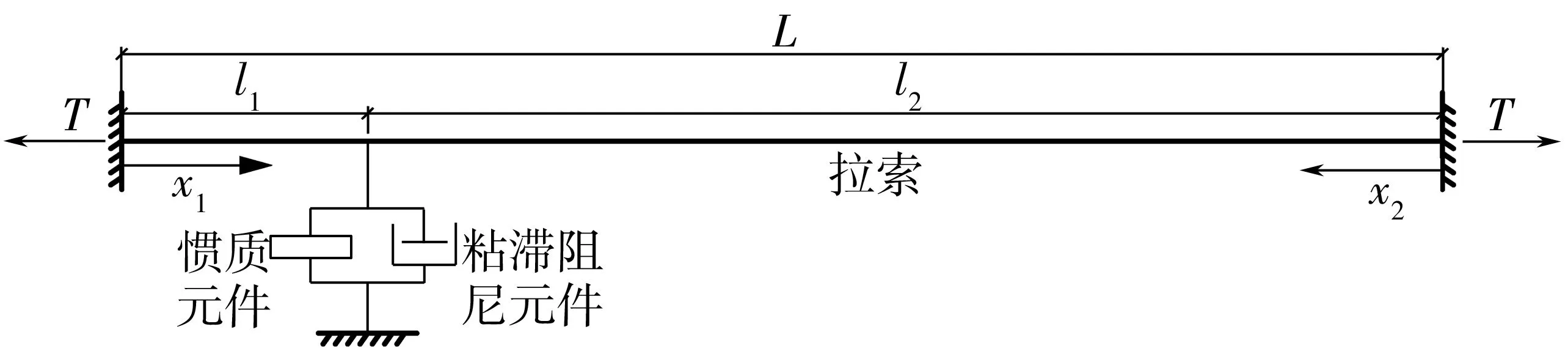
图3 拉索-惯质阻尼器系统分析模型Fig. 3 Analysis model of cable-inertia damper system

为简化分析，设拉索为张紧弦，不考虑其垂度、抗弯刚度和自身阻尼的影响。拉索的分段动力特性方程为：

(6)

式中：vk为各段拉索的横向位移，k=1,2；xk为各段拉索的纵向坐标，k=1,2。

式(6)在拉索上除阻尼器安装点外处处成立，可由以下边界条件求解：

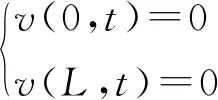
(7)

由分离变量法可知，满足微分方程(6)的解具有以下形式：

(8)

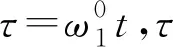
3.1 拉索-惯质阻尼器系统复模态分析

惯质阻尼器安装点的竖向平衡方程为：

(9)

与此同时，拉索的运动方程为：

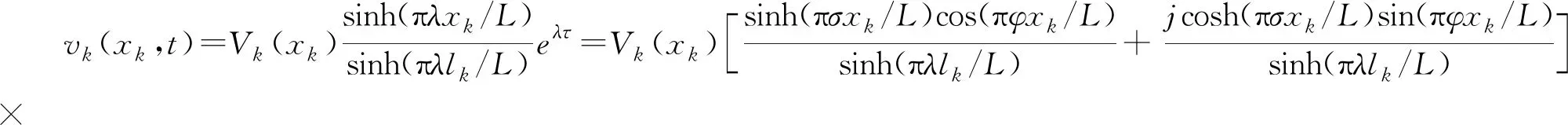
eστ[cos(φτ)+jsin(φτ)]

(10)

对于拉索-质量型阻尼器系统的每一阶振动，将式(10)带入式(9)，可得：

(11)

式中：μ=bd/mL为质量比。

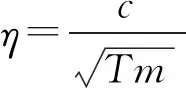
(12)

通过MATLAB，使用不动点迭代法对式(12)求解，并将方程计算过程验证。

3.2 方程验证

取极限条件，将式(12)中的质量比取为0，则该阻尼器可简化为黏滞阻尼器。与文献[20]所述的黏滞阻尼器进行比较，文献中最佳黏性阻尼系数ηopt和对应的模态阻尼比ζopt已由文献中式(25)、式(26)给出。按文献[20]所提供的方法，当阻尼器安装位置为5%索长时，第一、二和三阶最优黏滞系数ηopt分别为6.36、3.18和2.12，对应的一、二和三阶模态阻尼比近似为2.5%。为验证式(12)迭代方法的正确性，分别将第一、二和三阶的ηopt带入MATLAB计算，得出的第一、二和三阶模态阻尼比分别为2.64%、2.68%和2.74%，与文献[20]中所给出的近似值相差不大。笔者所使用的迭代计算方法具有较高准确性，以此为基础开展后续分析。

4 实际拉索算例与设计

4.1 新型惯质阻尼器的拉索减振效果

对比惯质阻尼器与黏滞阻尼器和减振效果。某桥梁工程中的拉索参数如表1。

表1 某实际桥梁工程中的拉索参数Table 1 Cable parameters of an actual bridge project

根据分析结果，以拉索的前三阶振动，开展惯质阻尼器的减振效果分析。

控制拉索前三阶振动的多参数分析如图4，图中横坐标η(l1/L)为阻尼系数，纵坐标μ为质量比，竖坐标ζ/(l1/L)为模态阻尼。分别控制一、二、三阶振动，前三阶振动最优结果如表2。

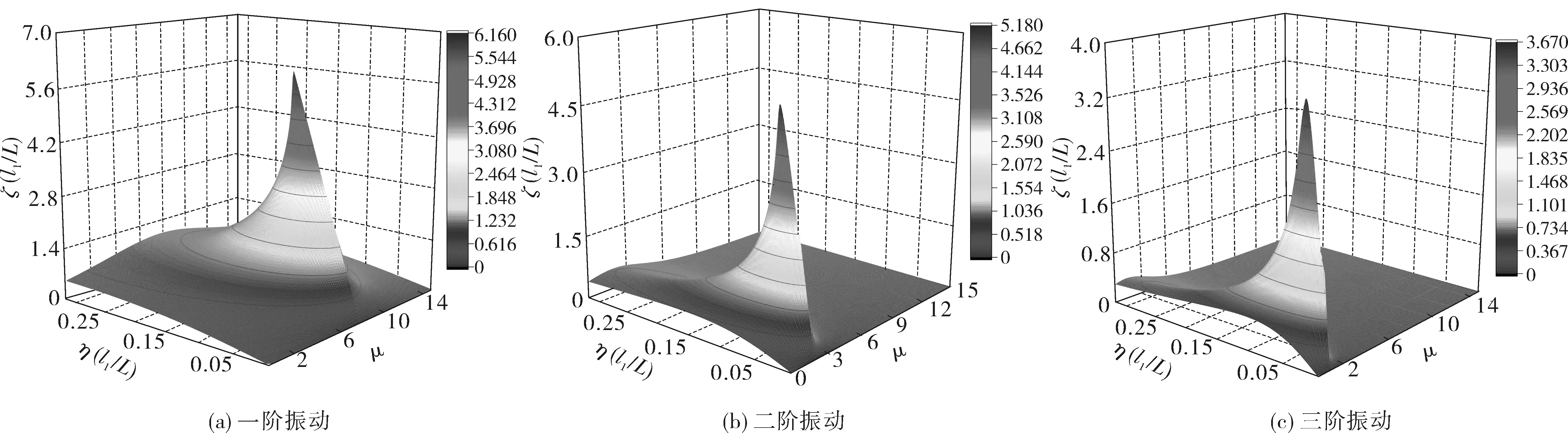
图4 拉索前三阶振动多参数分析Fig. 4 Multi-parameter analysis of the first three order vibration of cable

由表2可知：

1)为了抑制较低阶的振动，惯质类阻尼器需要较大的惯质。随着振动阶数增加，在达到最优模态阻尼时，阶数越高则所需的惯质越小。各阶振动间为达到最优减振效果所需要的惯质差距较大，由抑制一阶振动的7.7倍逐步变为抑制第三阶振动所需要的0.9倍。

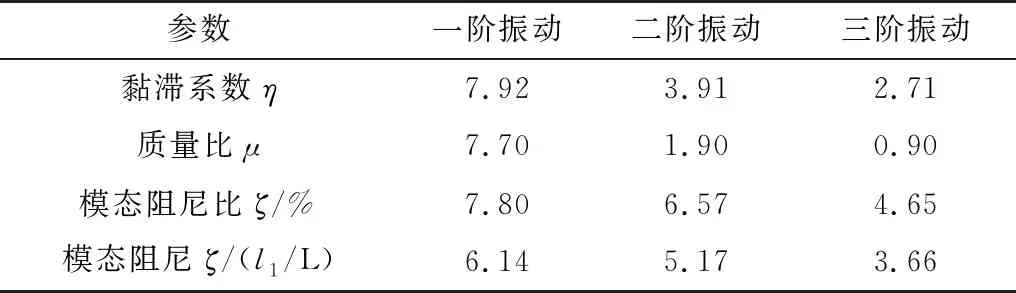
表2 前三阶振动最优结果Table 2 Summary of optimal results of the first three order vibration

2)黏滞系数有类似趋势，随着阶数升高，黏滞系数呈现出逐渐递减的趋势，为抑制第三阶振动，黏滞系数从第一阶的7.92降低至2.71。

3)惯质类阻尼器在经过调谐之后对抑制单阶振动有较好效果，经过参数最优处理之后，即使在安装位置为较低时(即拉索全长的1.27%)，第三阶振动阻尼仍能达到较为理想的3.66。

综上，惯质阻尼器对单阶振动具有较好的减振效果

5 惯质阻尼器多阶减振广谱性分析

经过参数最优处理之后，阻尼器的减振性能能够针对特定振动阶次达到较高的阻尼水平。但针对风雨激振等引起的高阶振动[15-16]仍需要进行更高阶的广谱减振分析。但是针对惯质类阻尼器的某一特定的阻尼器参数，进行同时抑制多阶振动的“广谱减振”[17]研究还处于起步阶段。笔者在针对不同安装位置、不同质量比的惯质类阻尼器，对其多阶广谱减振特性进行了分析，并与普通黏滞阻尼器进行比较。

图5为阻尼器安装位置l1/L=1.27%时，拉索前八阶振动的模态阻尼曲线，M1～M9分别表示一阶至八阶振动的模态阻尼曲线。图5(a)中μ=0，可认为是拉索安装普通黏滞阻尼器时前八阶振动的模态阻尼曲线，图5(b)、(c)、(d)与(e)分别表示μ为0.1、0.2、0.5、0.8时的阻尼曲线。M1与M4的交点M1&M4表示前四阶广谱减振的最优点，M1与M8的交点M1&M8表示前八阶广谱减振最优点。在μ为0.5、0.8时其低阶振动减振效果较好，但M1与M8不存在交点，所以无法同时达到前八阶最优。

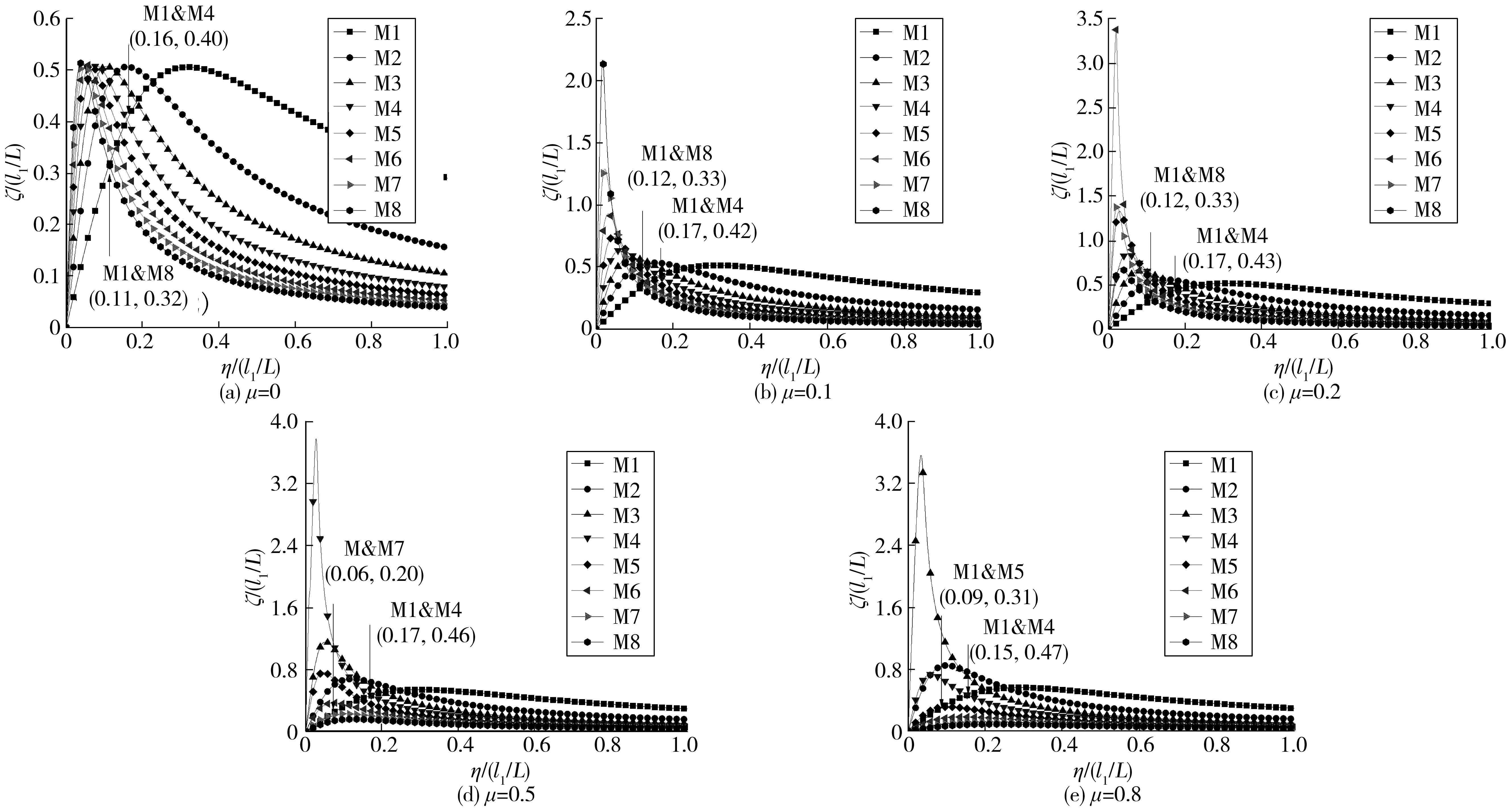
图5 l1/L=1.27%,μ取不同值时的附加惯质阻尼器拉索模态阻尼曲线Fig. 5 Modal damping curve of cable with additional inertia damper with l1/L=1.27% and μ with different value

图6为阻尼器安装位置l1/L=2.00%时，拉索前八阶振动模态阻尼曲线。图6(a)中μ=0，可认为是拉索安装普通黏滞阻尼器时前八阶振动模态阻尼曲线，图6(b)、(c)、(d)与(e)分别表示μ为0.1、0.2、0.5、0.8时的模态阻尼曲线。在μ为0.5、0.8时其低阶振动的减振效果较好，但M1与M8不存在交点，所以无法同时达到前八阶最优。

图7为阻尼器安装位置l1/L=3.00%，μ为0、0.1、0.2、0.5、0.8时拉索前八阶模态阻尼曲线。

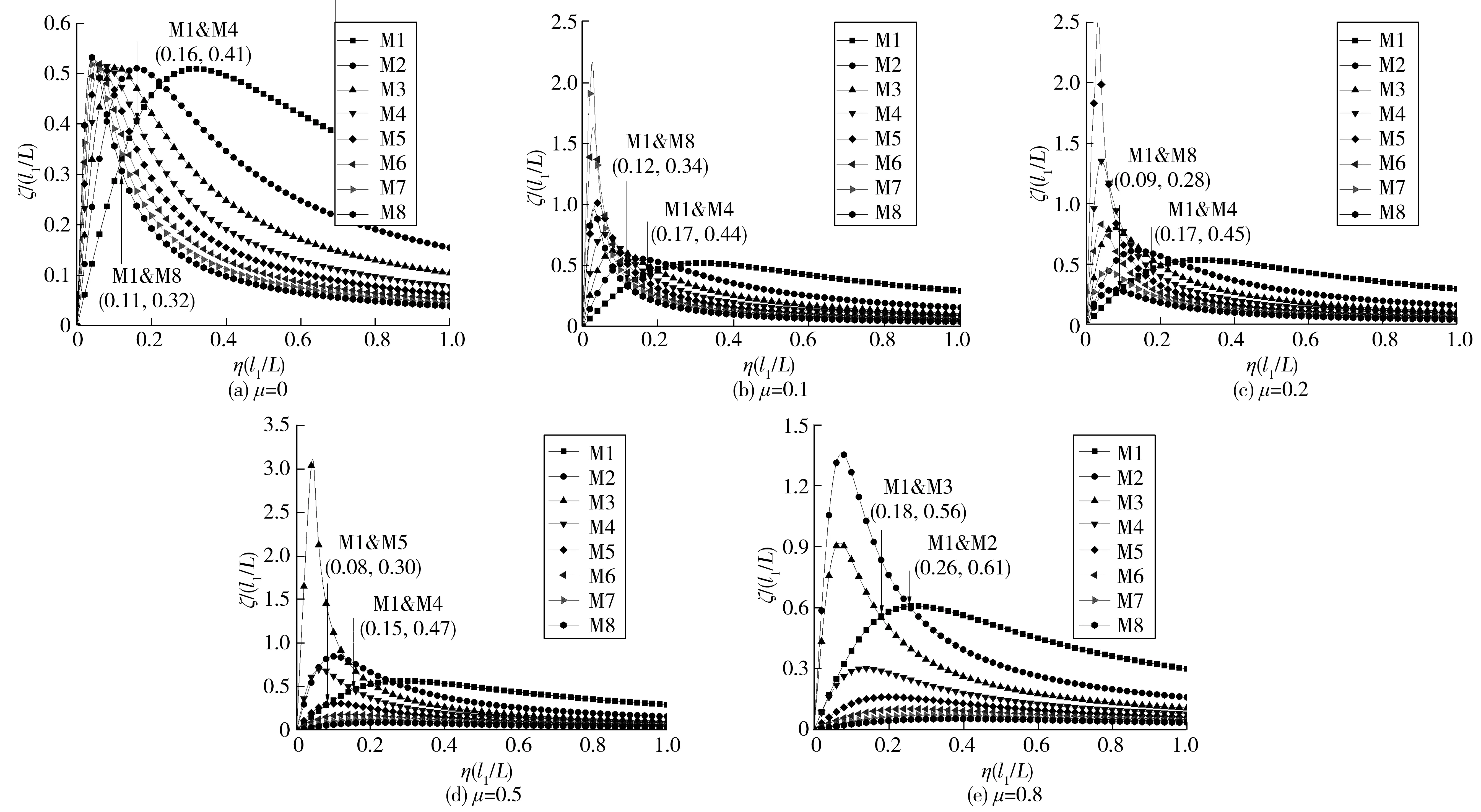
图6 l1/L=2.00%, μ取不同值时的附加惯质阻尼器拉索模态阻尼曲线Fig. 6 Modal damping curve of cable with additional inertia damper with l1/L=2.00% and μ with different value

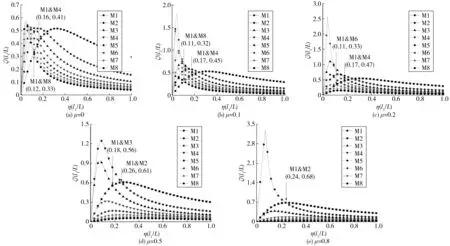
图7 l1/L=3.00%, μ取不同值时的附加惯质阻尼器拉索模态阻尼曲线Fig. 7 Modal damping curve of cable with additional inertia damper with l1/L=3.00% and μ with different value

图5～图7计算结果及惯质黏滞阻尼器相比于黏滞阻尼器的增幅效果如表3。由表3可知：当阻尼器安装位置较低，如l1/L不超过2%，且μ=0.1时，惯质阻尼器相比于黏滞阻尼器的广谱减振结果均有提高，但无论是前四阶减振结果还是前八阶的广谱减振结果均提高有限(10%以内)。当提高质量比后，较低阶广谱减振效果有大幅度提高(超过10%)，但是较高阶广谱减振效果严重降低，高阶广谱减振效果甚至低于现有的黏滞阻尼器。高阶广谱减振效果随着质量比μ的增长有“先增高后降低”的趋势。出现这种情况，是因为对于较低阶振动惯质阻尼器中，负刚度项-bdω2的存在增大了拉索在阻尼器处的位移，使拉索具有更“柔”的特性，加快了黏滞阻尼元件叶片的旋转速度，使黏滞阻尼器消耗更多的振动能量。同时对于高阶高频振动，较高的负刚度项对于拉索起到了较强的“嵌固作用”，导致了高阶减振效果大幅降低。提高阻尼器的安装位置，如l1/L>3.00%时，惯质阻尼器对于高阶广谱减振效果的“嵌固作用”更为明显，甚至当质量比μ=0.1时，前八阶广谱减振效果就相比黏滞阻尼器降低了3%。

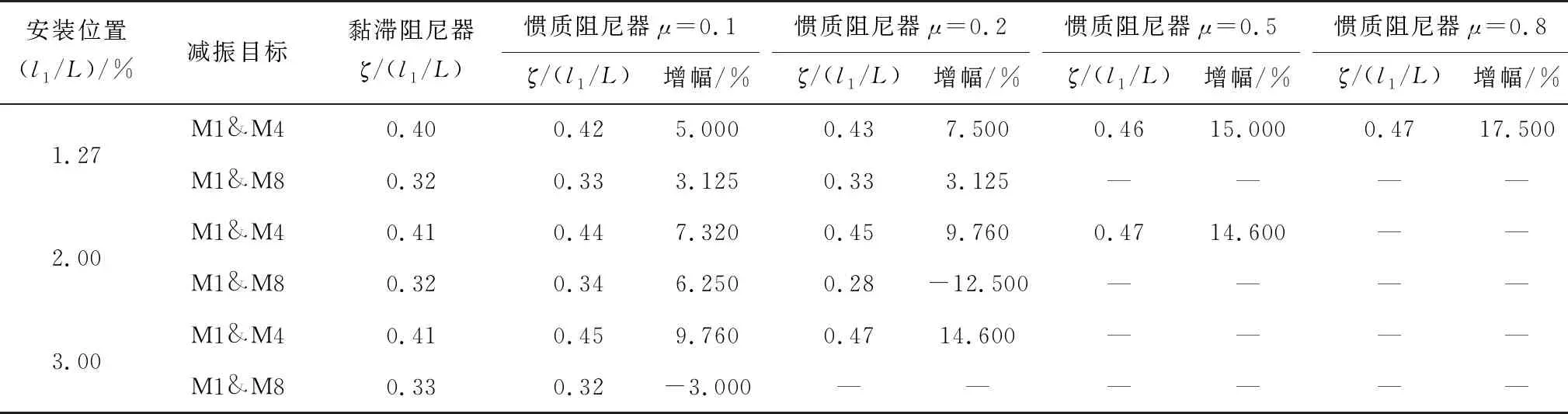
表3 广谱减振结果汇总Table 3 Summary of broad-spectrum damping results

6 新型惯质阻尼器的实用性分析

为了满足工程的实际应用，以表1中某实际工程拉索为例，其阻尼器安装位置为l1/L=1.27%。结合第一、二和三阶减振及前八阶广谱减振的各减振参数的需求，给出了满足其减振指标的阻尼器各参数，并根据式(2)、式(3)给出了质量放大倍数和黏滞阻尼放大倍数。惯质阻尼器用较低的物理质量和较低的黏度系数，就能起到预期的减振作用。针对前八阶做广谱减振分析，可得到惯质圆盘提供的惯质为10 733.76 kg,为拉索总重的20%，但其实际物理质量为37.24 kg，易于工程实践，计算结果如表4。

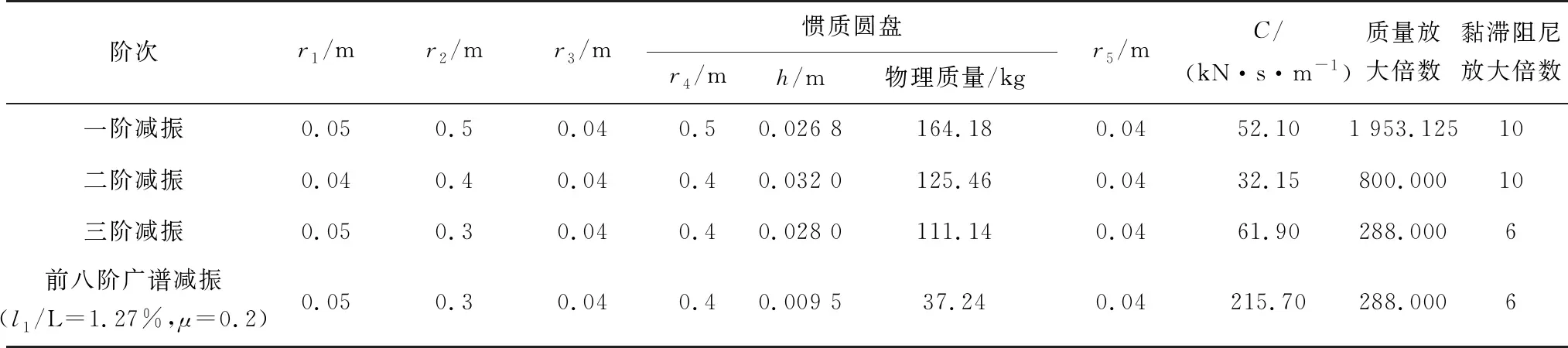
表4 阻尼器物理参数及质量、黏滞阻尼放大倍数Table 4 Physical parameters, mass and magnification of viscous damping of damper

7 结 论

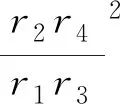
2)惯质阻尼器在经过调谐之后，有着很强的单阶减振能力，其减振能力优于现有黏滞阻尼器一个数量级。

3)对于高阶广谱振动控制，惯质类阻尼器的安装位置不宜太高，在抑制高阶振动时，所需要的惯质较小，仅为索总重的10%～20%左右；在抑制低阶振动时所需要的惯质较大，阻尼器所要提供的惯质接近或者超过索总重。以实际工程为例，拉索安装位置为索长的1.27%，针对前八阶做广谱减振分析，惯质圆盘提供的惯质为拉索总重的20%，但其实际物理质量为37.24 kg，易于工程实践也提高了阻尼器的广谱减振效果。

4)在实际工程应用中，惯质bd和黏滞阻尼系数cd均可按照笔者所提出的式(2)、式(3)进行计算，且要根据控制的目标模态来进行bd和cd的设计。提出的设计方法具有较好的工程指导意义，论证了实际工程应用的可行性。