X射线荧光光谱结合支持向量机对眼药水塑料瓶的分类研究

李若琳，陈丽萍，姜 红，杨 俊，满 吉

(1.中国人民公安大学 侦查学院，北京 100038；2.北京华仪宏盛技术有限公司，北京 100123)

0 前言

眼药水是人们生活中常用的药物，常常出现在各类案发现场中。作为药物，眼药水有着相对特定的成分，且其液体形态不易于保存，因而难以通过检验进行区分。而眼药水的包装瓶成分则相对固定，大多是以低密度聚乙烯(LDPE)、聚氯乙烯(PVC)、聚对苯二甲酸乙二醇酯(PET)等为主要材料的塑料包装瓶，具有防穿透、防泄漏、耐酸碱等特性。厂家在生产时，为满足眼药水塑料瓶的各项要求，往往会加入不同填料作为催化剂或着色剂等[1]，而在不同品牌、厂家、批次的眼药水塑料瓶中,这些助剂的成分往往不尽相同，故可据此对不同的眼药水塑料瓶进行区分。目前检验塑料物证的方法主要有：红外光谱法[2]、拉曼光谱法[3]、X射线荧光光谱法(XRF)[4]、裂解气相色谱法[5]等。其中,XRF以无损、微区等特性[6]，被广泛应用于物证鉴定领域。由于眼药水塑料瓶属于塑料，故以上方法可应用于对眼药水塑料瓶的检验。

上述检测方法中，有些针对有机成分，在前期研究成果中已利用差分拉曼光谱对实验样品中的有机成分进行了检测与分析[7]。XRF则针对于元素种类及含量进行分析，眼药水塑料瓶的有机成分种类相对固定，其区分度在于无机填料的不同；同时，XRF具有方法简单、速度、实验设备便携等优点，可以做到对物证进行现场定性定量检验。因此,笔者利用XRF对33个不同厂家、不同品牌、不同批次的眼药水塑料瓶样品进行检验，结合聚类分析对样品进行分类，依据分类的结果构建支持向量机(SVM)模型[8]，分别通过一对一法构建多元分类器[9]和K-fold交叉验证[10]的方法成功构建了SVM模型，对样品数据进行机器学习，证明了SVM模型能够实现对未知眼药水塑料瓶的分类判断，为公安工作中对未知眼药水瓶进行识别分类提供了参考。

1 实验部分

1.1 仪器及条件

实验采用北京华仪宏盛技术有限公司X-MET8000型XRF光谱仪进行测试，实验条件为：检测电流200 μA、电压50 kV、功率10 W、测试时间60 s。

1.2 实验样品

不同厂家、不同品牌、不同批次的眼药水塑料瓶样品33个(见表1),样品分为透明与不透明两类，透明样品的颜色包括无色、红色、棕色、蓝色等，不透明样品均为白色。

表1 眼药水塑料瓶样品表

1.3 实验方法

1.3.1 重现性实验

为验证XRF检验结果的稳定可靠性，对随机选取的9#样品进行10次连续测定。

1.3.2 对样品进行实验

购买、收集市面上常见的不同厂家、品牌、批次的眼药水塑料瓶作为样品，对样品编号后用酒精棉球擦拭样品并待其风干，按次序将眼药水塑料瓶样品置于XRF光谱仪采样口进行测定，保持实验条件不变，取3次测定的XRF光谱仪数据平均值。得到数据后，首先对样品进行分类并运用系统聚类方法对分类结果进行检验，其次通过python编程构建SVM模型，对样品的分类结果进行学习，最终实现对未知样品类别的判断。

2 结果与分析

2.1 重现性实验的结果与分析

对9#样品的连续10次X射线荧光光谱测定结果见表2。由表2可得：9#样品平均w(Cl)为596 μg/g，标准偏差为4.23 μg/g，相对标准偏差为0.71%；平均w(Ti)为264 μg/g，标准偏差为8.31 μg/g，相对标准偏差为3.15%；平均w(Fe)为34 μg/g，标准偏差为1.57 μg/g，相对标准偏差为4.61%；平均w(Sb)为224 μg/g，标准偏差为3.75 μg/g，相对标准偏差为1.68%。各元素检测结果的相对标准偏差均小于5%，表明XRF对眼药水塑料瓶成分的检验准确可行。

表2 9#样品的10次测定结果

2.2 XRF对样品的检验结果与成分分析

33个样品的元素成分及相对含量检验结果见表3。

表3 样品的X射线荧光检验结果

目前市面上眼药水瓶大多以LDPE、PVC、PET等为主要材料，在前期研究结果中得知，33个样品中有15个样品的主要成分为PET，另外18个样品的主要成分为聚乙烯(PE)。在此基础上，对样品中各填料成分进行分析，其中钙元素来自于填料碳酸钙，碳酸钙是目前应用范围最广的无机粉体材料[11]。钛元素来自于钛白粉，钛白粉加入塑料中可提高塑料的多项应用性能指标[12]，在塑料工业中被广泛应用。在塑料的生产中，常存在含铁的催化剂、填料、着色剂，故样品中普遍含有少量铁元素。三氧化二锑具有良好阻燃作用，也可用作着色剂、催化剂等[13]，可推测实验结果中锑元素由此而来。钡元素来自于硫酸钡，硫酸钡作为塑料工业中的常用填料，在塑料改性中起到重要作用。

2.3 样品的分类

2.3.1 人工分类

根据实验结果，可得到各样品的三维柱状图(见图1)，其中，由于在含有钛元素的样品中，钛元素质量分数普遍远高于其他元素含量，为直观反应各样品的成分构成及比例，仅取其质量分数的百分之一进行制图。

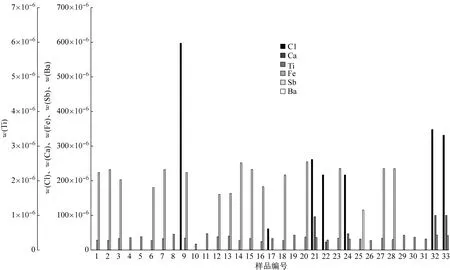
图1 样品检验结果的三维柱形图

对各样品的成分进行分析，结合三维柱形图，可将样品分为4类(见表4)。Ⅰ类样品中，除12#样品和18#样品含有少量钙元素以外，所有样品都仅含有锑元素和铁元素，且二者质量比为6～8。

表4 眼药水塑料瓶样品人工分类结果

Ⅱ类样品均只含有铁元素，较为纯净，含有的填料较少。Ⅲ类样品均含有氯元素，是以PVC为主要原料制成的眼药水塑料瓶。11#样品成分中仅含有铁元素和钙元素，13#样品成分中含有较多钙元素，25#样品成分中含有钡元素，这3个样品均难以归类到以上3个分类中，故将这3个样品归为Ⅳ类。

2.3.2 SPSS系统聚类

考虑到人工分类具有一定的主观性，故采取机器分类的方法对人工分类的结果进行检验。系统聚类法[14]是使每个样品各为一类，确定其相似统计量，然后合并最接近的两类或若干类，重新计算类别间的相似性统计量并再次进行合并，直至最后一类包含所有样品时结束合并。

利用SPSS软件，分别选择组间连接、平方欧氏距离作为度量，对数据采取Z得分标准化处理，聚类结果见图2，表5为系统聚类过程中组内平方误差和(SSE)。

图2 眼药水塑料瓶样品系统聚类结果

根据表5内数据绘制聚类类别数与SSE的关系图，结果见图3。

表5 系统聚类组内平方误差数据

由图3可以看出：随着聚类类别数的增多，SSE逐渐减小，当类别数为7时出现拐点，此后SSE减缓速度变慢，增大聚类数并不能使分类效果得到进一步增强。因此，采取类别数为7，此时并类距离为5，分类结果见表6。

表6 眼药水塑料瓶样品系统聚类分类结果

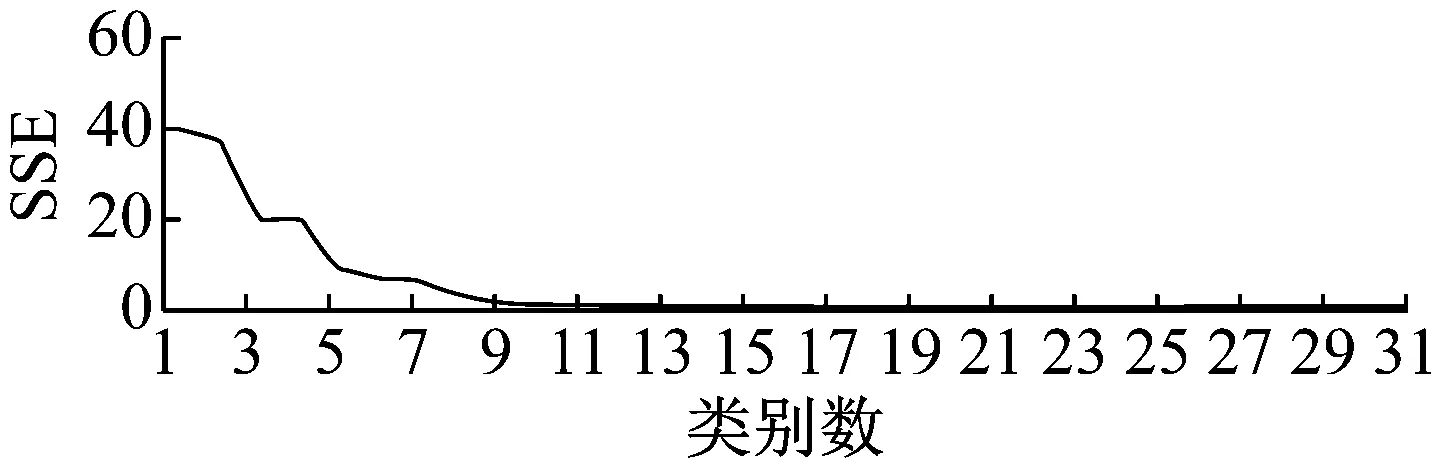
图3 系统聚类类别数与SSE关系的折线图

为便于统计，防止在后续机器学习过程中因样品太少导致不具备普遍性，使机器学习结果产生偏差，故将仅含有1种样品的E、F、G3类合并为1类，归于“其他”类别，即将样品分成了4类。将该分类结果与人工分类得到的结果相比发现，A类与第Ⅱ类完全一致，B类与第Ⅰ类基本一致，C类与第Ⅲ类基本一致，其他类与第Ⅳ类基本一致，将这4组相对应，33个样品中2种分类方法得到结果相同的有27个，即人工分类与系统聚类结果的一致性达到82.00%，证明人工分类的结果具有较高的准确性，可以应用于后续对数据的分析中。

2.4 基于SVM的预测建模

SVM是一种机器学习算法，依托于统计学原理，应用于数据的分类与回归分析[15]，具有保证局部最优解为全局最优解等优点，其目的是实现对数据集的正确分类，得到具备最大几何间隔的分离超平面。在实践中，可以根据具体需要采取不同的编程方式构建SVM模型，对数据进行学习，实现对样品数据所属类别的判断。在实践中，可以采取python、matlab、C++等多种途径构建SVM模型，其最终运行结果并无区别，在本实验中选择python进行构建。

在之前对数据的分类处理中，已经将样品分为了4类，根据这4类样品的分类结果，可以构建SVM模型对其进行学习，以判断未知眼药水瓶的具体分类。通过python编写代码，选择采取划分训练集与预测集进行预测建模以及K-fold交叉验证进行预测建模的2种方法，分别构建SVM模型，比较二者的预测准确率，判断构建SVM的可行性，并找到更合适于本实验得到数据结果的SVM模型构建方法。

2.4.1 划分训练集与预测集进行预测建模

作为二值分类器，SVM适用于解决二元分类问题，而此次实验中样品被分为4类。为实现对样品类别的准确判断，采用一对一法构造多元分类器[16]。

在python编程过程中，首先将实验中得到的样品数据划分为训练集与预测集，训练集包含24个样品，预测集包含9个样品。在训练集数据中，根据表3中的4类样品，在每2个分类间构建1个SVM模型，得到6个训练组，即Ⅰ与Ⅱ、Ⅰ与Ⅲ、Ⅰ与Ⅳ、Ⅱ与Ⅲ、Ⅱ与Ⅳ、Ⅲ与Ⅳ，每个训练组得到1个训练结果。将预测集中待预测样品分别对6个结果进行测试，并通过投票得出最终分类结果，得到的混淆矩阵见图4。

图4 测试集混淆矩阵

混淆矩阵可直观体现预测准确度[17]，其中矩阵中的数值表示真实数据被预测为此类的数量。由图4可知，预测集中有3个样品被预测错误，该模型预测准确率为66.67%。

2.4.2 K-fold交叉验证进行预测建模

交叉验证是用于检测分类器模型性能的一种方法[18],将数据分为训练集与验证集，训练集用于机器学习，验证集用于验证训练结果。交叉验证可以较客观地评价模型对训练集之外数据的预测准确度，常用方法有留出法[19]、留一法[20]、K-fold 交叉验证法[21]等。

K-fold交叉验证是将数据分为k个不相交的子集，每次取1个子集作为测试集，其他数据则作为训练集，得到1次误差，最终根据k个子集得到k个误差，取所有误差的加权平均得到总评分，即为该模型的预测准确率。K-fold交叉验证可使每个数据都参与到训练中，做到对有限的数据进行充分利用。

该模型同样选择python进行构建。在编程过程中，首先将33个样品数据随机均分为3组，每组数据轮流作为预测集，当1组数据作为预测集时，将另外2组数据合并作为训练集，1对训练集与预测集构建1个SVM模型，最终一共得到了3个模型，分别命名为K1、K2、K3，这3个模型的得分(分类准确率)见表7。

表7 K-fold交叉验证得分结果

由表7计算得到加权平均误差为0.848 5，根据该方法的原理可知此交叉验证模型的加权平均误差即为总得分，该模型总得分为0.848 5，即预测准确率为84.85%。

将以上2种构建SVM模型的方法相比较，K-fold交叉验证方法的准确率较高，更加准确可行。采取K-fold交叉验证的方法，可以实现对未知眼药水瓶类别的判断。

3 结语

通过XRF对33个不同厂家、不同品牌、不同批次的眼药水塑料瓶样品进行了快速、无损、准确、科学的成分鉴定，对样品分类并采取系统聚类法检验分类结果，然后通过一对一法和K-fold交叉验证法构建SVM，分别得到了66.67%和84.85%的预测准确率，表明对于该实验样品，K-fold交叉验证法构建SVM能更加准确地识别眼药水塑料瓶的类别，为未知眼药水塑料瓶的快速分类与鉴别提供了较可行的参考方法。

基于本研究，在本实验样品分类的基础上，可以在有其他样品作为参考的情况下，对本实验中难以分类的眼药水塑料瓶采取更加合理的分类方式。同时，考虑到依托大量数据构建的SVM模型具有更高的预测准确率，下一步可依照厂家、品牌、批次等不同因素，建立眼药水塑料瓶的X射线荧光光谱数据库并依此优化SVM模型，从而实现在实践中对未知眼药水塑料瓶的快速识别，为公安机关案件侦破提供新思路。