车辆纵向跟车舒适性模型预测控制算法研究
2022-02-08胡趁义龙永文
徐 哲,胡趁义,龙永文,刘 豪
(重庆理工大学 汽车零部件先进制造技术教育部重点实验室, 重庆 400054)
0 引言
随着科学技术的不断发展,自适应巡航系统广泛应用于现代汽车[1]。自适应巡航控制系统主要有两大功能,分别是定速巡航和跟踪前车。其中,纵向跟车对于缓解驾驶员的疲劳,以及改善交通环境起到了重要的作用。武汉理工大学李想等[2]提出了一种变权重系数的线性二次型最优控制算法,使用采集的车辆速度建立模糊控制器,再通过动态选取线性二次型调节器中的权重系数,最终得到在全速域范围最优的目标加速度;翟志强等[3]提出了一种基于可变间距的车辆跟驰控制策略。无论是变权重系数还是可变车距,都是为了提高安全跟车性能,并未考虑舒适性。随着现代生活水平的不断提高,乘坐舒适性也逐渐成为人们出行的必备要求。虽然在跟车过程中行车安全性和舒适性不能兼得,但是能够在保证安全性的前提下考虑舒适性要求。由于前车加速度的变化会影响自车的舒适性,故不能忽略前车加速度,本文将引入前车加速度作为干扰量,对跟车舒适性进行研究。
本文在保证安全性的前提下,通过模型预测控制算法设计纵向跟车控制器,将前车的加速度作为扰动量,通过考虑车辆的相对速度和相对距离以及自车状态量,搭建纵向舒适性跟车的控制模型,最后通过Simulink和CarSim联合仿真验证算法的有效性和稳定性,实现对乘坐舒适性的要求以及对目标车辆的精确跟踪。
1 纵向跟车模型控制的建立
自动驾驶车辆的纵向跟车控制系统主要是根据目标车辆的行驶状态来计算自车的期望加速度。首先建立车距模型,然后通过模型预测控制算法求解纵向跟车控制的期望加速度,通过期望加速度计算车辆差速器的扭矩,最后通过扭矩控制车辆的跟车控制。
1.1 车距模型的建立
安全车距[4]是跟随目标车辆时自车期望与前车保持的纵向距离,它是跟车控制系统的主要控制策略之一,研究车辆纵向跟车控制。安全车距是最重要的参数,并且它又作为模型预测控制器的输入,因此安全车距的设计会直接影响车辆跟车的安全性和道路通过性。
安全车距直接影响驾驶安全性和道路使用率。如果安全车距过大,两车的间距就会较大,会影响后方车辆的行驶,浪费道路的使用率;如果间距过小,两车之间的距离就会较小,前车遇到紧急情况时紧急刹车,会导致后方车辆出现追尾事故,给驾驶安全性带来压力。安全距离是最小停车距离与当前车速的函数[5]。
目前大部分安全车距研究可分成3种策略:固定车距、定时距和变时距。固定车距是使自车与前车的距离设定为定值,这种策略不符合驾驶员的驾驶习惯,而且不能满足舒适性的要求;定时距(constant time headway,CTH)和变时距(variable time headway,VTH)[6]的不同之处就是车间时距是否是恒定的。变时距是指安全车距可随着车速等因素的变化而调整,这样能够适应更复杂的行驶环境,并且适应性较强,能够满足不同车况和工况下驾驶员的需求[7]。定时距是指车间时距是固定的,虽然定时距模型对于一些复杂路况控制表现不是特别好,但是由于它计算简单,能够实现驾驶员的基本要求,稳定性又好,所以广大学者和厂商在研究安全车间距中广泛采用定时距模型。
由于在实际的行驶过程中,前车速度难以实时得到,为了防止在行驶过程中前车速度突然发生变化而导致系统不稳定,采用定时距计算期望距离:
ddes=τ·v+d0
(1)
式中:ddes为期望跟车距离;τ为车间时距,采用固定值,取值范围为1.4~2.8 s[8],本文选择2.0 s;v为自车的实际车速(m/s);d0为两车之间的最小安全距离(m),取值为3~8 m,本文选取5 m。
1.2 运动学模型建立
基于模型预测控制原理设计纵向跟车控制器,通过图1所示的车辆纵向运动学关系建立所需的状态方程[9]。

图1 车辆纵向运动学关系示意图
图1中xh是自车的位置;xf是前车的位置,根据两车的相对运动关系,建立两车的运动关系方程式,如式(2)所示:

(2)
式中:drel为两车的实际车间距;ddes为两车之间的期望车间距;Δd为车间距误差;vf为前车的实际车速;vh为自车的实际车速。
车辆系统由于存在惯性,使车辆通过设计的控制器计算得到的期望加速度与实际行驶状态的加速度不相等,存在一定的延迟,故得到的期望加速度不能直接作为实际加速度使用,通常处理方法是采用一阶惯性系统描述,如式(3)所示:
(3)
式中,ades为期望加速度。
由以上描述可得到纵向跟车的状态方程式[10],如式(4)所示:
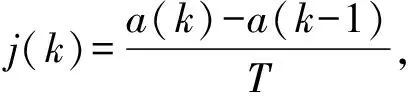
由离散方程可以得到对应的状态方程,选择x(k)作为状态量,x(k)=[Δd(k),Δv(k),ah(k),vh(k),j(k)]T。将前车加速度af作为扰动量,使模型更加接近真实情况。最终状态方程空间表达式可以表述为式(5)所示:
x(k+1)=Ax(k)+Bu(k)+Gw(k)
(5)
式中的A、B、G矩阵分别为状态矩阵、输入矩阵和扰动矩阵,具体表示如下:
其中,T为采样周期,本文选择为0.2;u=ades为系统控制输入;w=af为系统扰动量。
基于本文研究的需求,在自车行驶过程中当检测到目标车辆时,自车应该能够及时稳定跟踪前车车辆,即自车车速应当追随目标车辆车速,使两车车间距逐渐趋向于期望安全车间距。所以选择两车车间距误差、相对速度、自车加速度及自车加速度变化量作为系统输出量,输出方程可表示为如式(6)所示:
y(k)=cx(k)
(6)

上述模型就是本文纵向跟车的控制模型,其中y(k)=[Δd(k),Δv(k),ah(k),j(k)]T为输出量。为了能够更真实地反应车辆行驶状态,本文将目标车辆的加速度作为扰动量考虑进去,同时也将自车的加速度和加速度变化率作为优化目标加以考虑,这样不仅能提高跟车的精度也能提高舒适性。
2 纵向跟车控制算法设计
2.1 控制目的与约束分析
本文研究的基于MPC算法的纵向跟车控制系统兼顾了行驶安全性、跟车性、舒适性优化目标,对于每个目标都有相应的约束与之配合,针对每个约束进行分析,并整合所有约束添加到整个模型中进行求解,作用于控制系统[11-13]。
1) 行驶安全性约束
行驶安全性是避免自车与目标车辆碰撞,控制自车与目标车辆之间的实际车间距。为了提高行驶安全性,需要严格控制车辆的行车距离:
xf-xh≥d0
(7)
2) 跟车约束
跟车性是自车与目标车辆之间的实际车间距尽可能逼近期望车间距,即实际车间距与期望车间距的误差趋近于0,同时自车车速逐渐逼近目标车速,故此性能的约束条件为:
Δd→0, Δv→0当k→∞
(8)
3) 舒适性约束
舒适性是驾驶员的驾驶感受及乘客的乘车体验,通常是通过自车加速度的大小以及加速度变化率来评价[14],如果加速度变化率越小,车辆的舒适性就越高。本文对于自车加速度、期望加速度及加速度变化率的约束如下:
amin≤a(k)≤amax
(9)
umin≤u(k)≤umax
(10)
jmin≤j(k)≤jmax
(11)
式中:amin为加速度下限;amax为加速度上限;umin为期望加速度下限;umax为期望加速度上限;jmin为自车加速度变化率约束下限;jmax为自车加速度变化率约束上限。
此外,一般跟车过程中,在实现自车高效跟随目标车辆行驶的前提下尽可能使加速度及加速度变化率更小更平缓,这也是对于乘坐舒适性的一种保证,即约束目的为:
min|a(k)|, min|j(k)|
(12)
4) 速度约束
对于跟车控制,自车车速不仅会受到目标车辆的速度影响,还会受到我国道路交通法规限制,因此,对于自车车速进行约束,约束条件为:
vmin≤v(k)≤vmax
(13)
式中:vmin是自车车速下限;vmax是自车约束上限。
2.2 控制算法设计
根据上述建立的纵向跟车运动学模型,并将此模型作为MPC算法的预测模型,对自车在预测时域内做出预测计算:
(14)
(15)
其中:

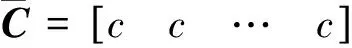
系统控制的目标是车间距和车速的跟踪精度,以及跟车过程中的舒适性,同时为了避免在规定的计算时间内无法得到最优解,故在惩罚函数内有必要增加松弛因子,其惩罚函数表达式如(16)所示:
(16)
式中:y(k+i|k)为控制输出预测值;yref(k+i|k)为控制输出参考值;(k+i|k)代表根据k时刻采样时刻的信息预测k+i时刻的值,其中i=1,2,…,Np;u(k+i)表示k+i时刻控制输入量,其中i=1,2,…,Nc-1;Q和R分别表示输出量和控制量的权重系统矩阵[15]。式(16)等号右侧的第一项反映了系统对车间距和速度的跟随能力,第二项反映了跟车舒适性的要求,整个表达式的功能是使自车稳定跟踪前车并且要满足舒适性的要求。
综合上述的设计目标及车辆自身的性能限制,对应的系统约束总体概述为:
(17)
模型预测控制原理是在满足约束条件(17)的前提下使惩罚函数(16)最小,每个控制周期解决如式(18)优化问题:

(18)

(19)
其中,
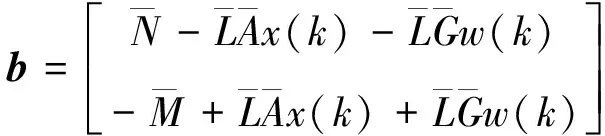
根据式(16)可以借助Matlab中的QP求解器进行求解,得到控制时域内的一系列控制输入量:
根据模型预测控制原理,从控制输入量序列中选取第一个元素u(k)作为实际的输入量作用于系统。当输入量序列的第一个元素作用于系统时,系统会在新的时刻预测出下一段时域的输出,然后通过优化过程得到一个新的控制量序列。重复以上步骤,直至系统完成整个控制过程。
3 纵向跟车控制的联合仿真验证
3.1 联合仿真模型的搭建
基于建立的纵向跟车模型,在Matlab/SimuLink平台中,结合CarSim进行仿真验证。首先在CarSim中建立两车的实车模型[15],其中前车根据设定的车速行驶,输出量是前车位置、前车速度、前车加速度;而自车设置起始车速,自车的行驶车速随节气门开度变化而变化,输出量为自车位置、自车车速及自车加速度,由于加速度变化率和上一刻的加速度有关,故本文采取延迟模块来计算,接着将前车的加速度、两车的相对距离、相对速度、自车的加速度、自车速度以及自车加速度的变化率导入基于MPC的纵向跟车模型,得到自车的期望加速度,最后通过差速器的扭矩和加速度的关系计算得到自车4个轮的扭矩,从而控制自车跟随目标车辆行驶。具体模型如图2所示。
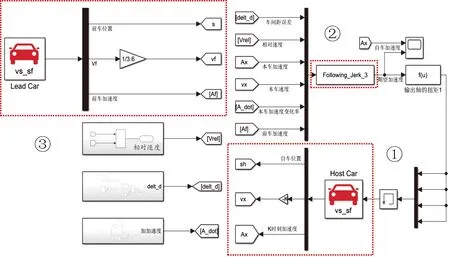
图2 基于MPC控制的纵向跟车模型示意图
图2是基于模型预测控制的纵向舒适性跟车模型,图中的①表示的是目标车辆的CarSim设置,②表示的是根据约束条件及目标设计的模型预测控制器,③表示的是自车的CarSim设置。
3.2 纵向跟车仿真参数
以设计的纵向跟车控制器为研究对象,采用的部分仿真参数[16]如表1所示。
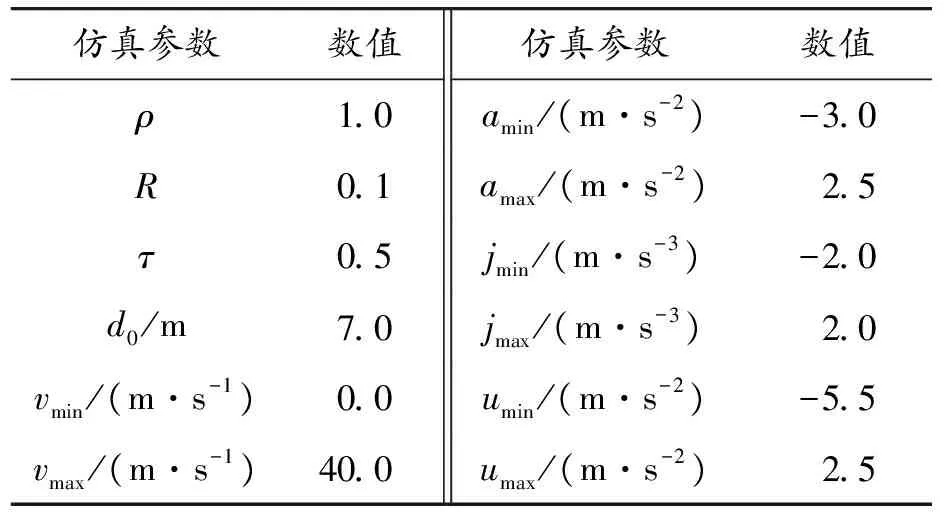
表1 部分仿真参数
3.3 纵向跟车联合仿真结果与分析
加速度变化率是评价舒适性的指标之一。因此,将所设计的控制器与未考虑自车加速度变化率的控制器在2种不同的行驶方案下进行对比分析,验证了本文所设计的纵向跟车控制器能够更好地实现舒适性跟车。图4中的j代表了自车加速度变化率,具体验证如下:
1) 目标车辆匀速行驶
目标车辆设置为以80 km/h匀速行驶,自车设置初始速度为30 km/h,在此条件下观察2种不同控制器的跟车效果,仿真结果如图3所示。
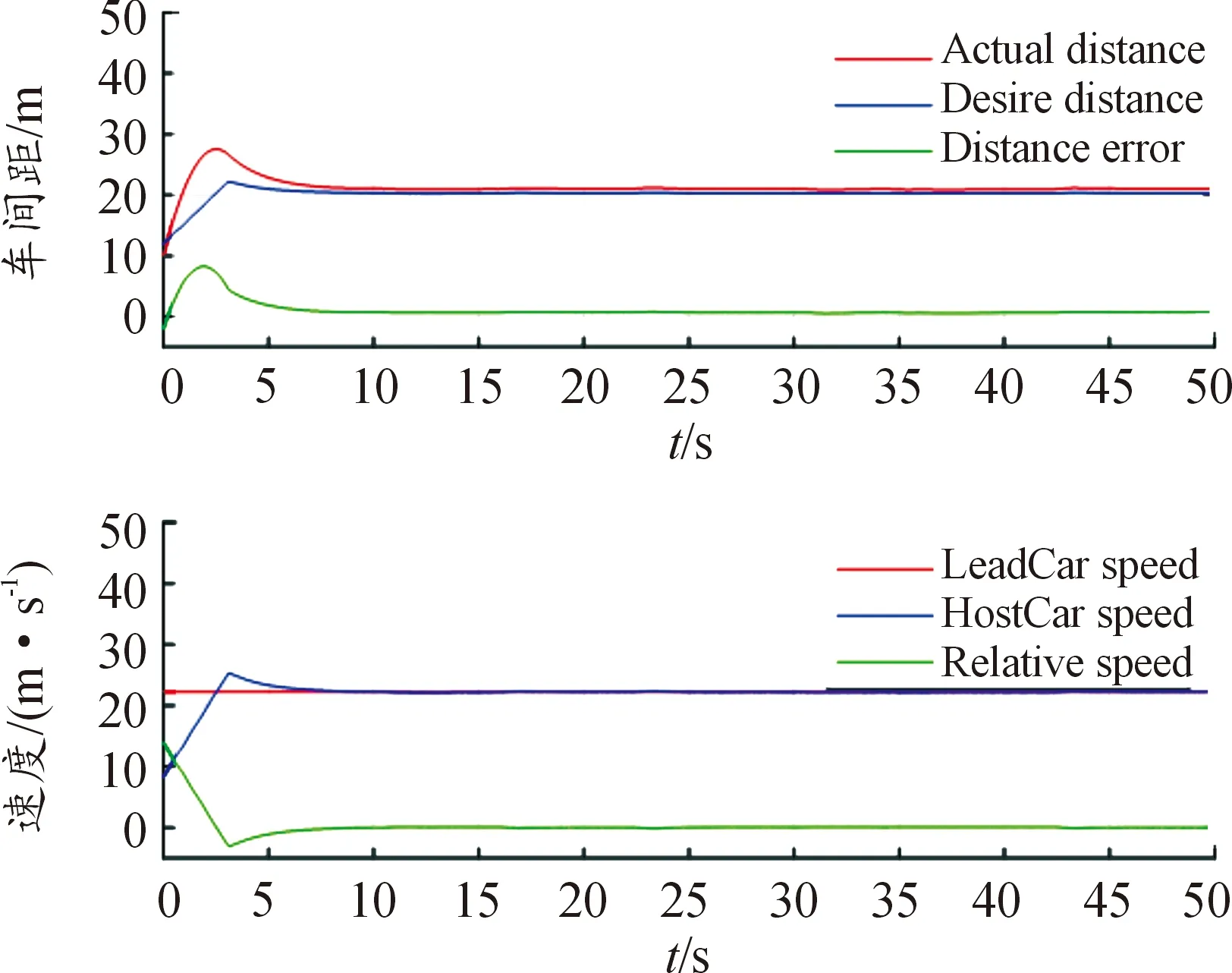
图3 未考虑j的车间距及速度曲线
图3是未考虑加速度变化率的仿真结果,其中图3中的上图描述的是实际车间距、期望车间距以及车间距误差曲线。从图可以得知,实际车间距与期望车间距有较小的误差,误差为0。图3中的下图描述的是目标车辆和自车的车速以及两者之间的相对速度。由图可知,自车车速能跟随目标车辆的车速,相对速度逼近于0。图3中的车间距误差以及相对速度均为0,说明了自车能够跟随目标车辆。图4是考虑了加速度变化率的仿真结果,图4中的上图得到的实际车间距等于期望车间距,车间距误差在5 s后也等于0;图4中下图得到的自车速度曲线在5 s后与前车速度曲线重合,相对速度曲线为0。从图4中得到车间距误差为0,相对速度也为0,说明自车能够跟随目标车辆。综上所述,无论是考虑加速度变化率,还是未考虑加速度变化率,自车都能够跟随目标车辆行驶。

图4 考虑j的车间距及速度曲线
图5是未考虑加速度变化率的目标车辆和自车的加速度曲线以及加速度变化率曲线。已知试验工况是目标车辆匀速行驶,因此在图5中目标车辆加速度为0,但是自车加速度在不断波动,从而导致自车加速度变化率也发生震荡,这样的结果会大幅度降低乘坐舒适性。
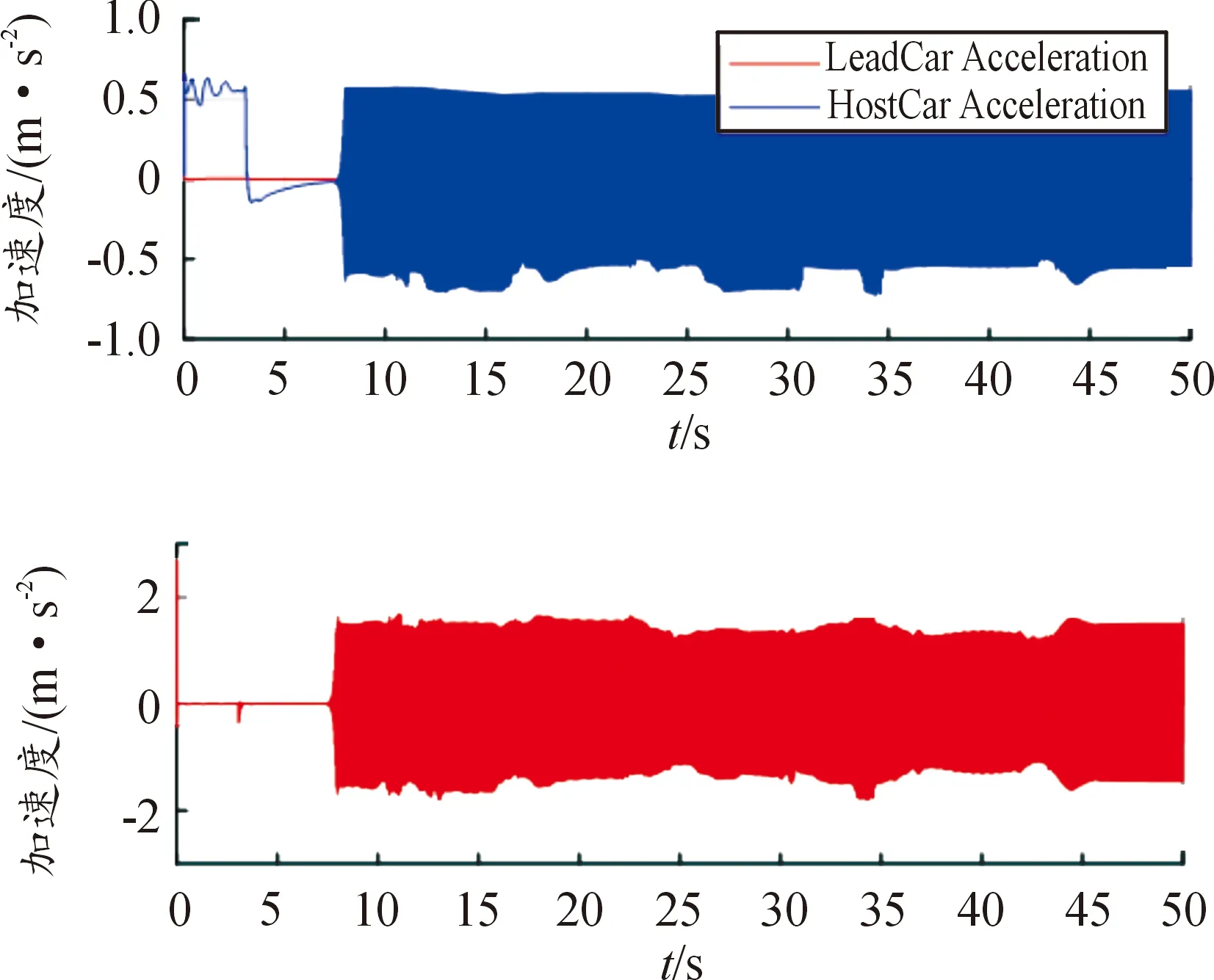
图5 未考虑j的加速度及加速度变化率曲线
图6是考虑了加速度变化率的仿真结果,从上图可以明显看出自车加速追赶目标车辆,当满足车间距要求后,自车会跟随前车速度行驶,故自车加速度经过短暂的变化,最终为0,而且通过加速度变化率曲线可知,自车在跟随前车行驶时,加速度变化率为0,因此,考虑自车加速度变化率的控制器能够提供更高的舒适性。
综上所述,考虑自车加速度变化率的控制器不仅能够实现纵向跟车,而且能够满足乘坐舒适性要求。
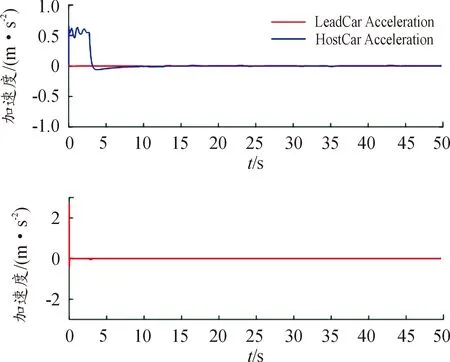
图6 考虑j的加速度及加速度变化率曲线
2)目标车辆变速行驶
为了能够模拟更真实的行驶环境,只考虑匀速行驶是远远不够的,故接下来的研究将目标车辆设置为变速行驶,其中包含加速、减速、匀速行驶,速度设置如图7所示。

图7 目标车辆变速行驶的速度设置曲线
自车跟随变速的目标车辆的仿真结果如图8、9所示。
图8和图9描述的是在跟随变速的目标车辆时,两车之间的实际车间距、期望车间距、车间距误差,以及各自的行驶速度和相对速度。从图8、9可知,2种控制器得到的车间距误差以及相对速度曲线都逼近于0,说明2种控制器控制的自车都能够实现纵向跟车。

图8 未考虑j的车间距与车速曲线

图9 考虑j的车间距与车速曲线
图10和图11描述的是两车的加速度及加速度变化率,图10中未考虑自车加速度变化率,仿真结果发现自车加速度会出现多处突变,而且加速度变化率出现了多段的震荡,这样的加速度会影响乘坐舒适性;而图11考虑了加速度变化率,从仿真结果可以看出加速度不会出现震荡,并且从加速度变化率曲线可知,加速度变化率相对稳定,故此控制器控制的自车在行驶过程中有更好的舒适性。
综上所述,考虑自车加速度变化率的控制器能够跟随变速的目标车辆,而且行驶过程中舒适性更好。
通过2种控制器对比可知,无论目标车辆是匀速行驶还是变速行驶,未考虑自车加速度变化率和考虑自车加速度变化率的控制器都能够实现纵向跟车,但是考虑自车加速度变化率的控制器有着更好的乘坐舒适性。
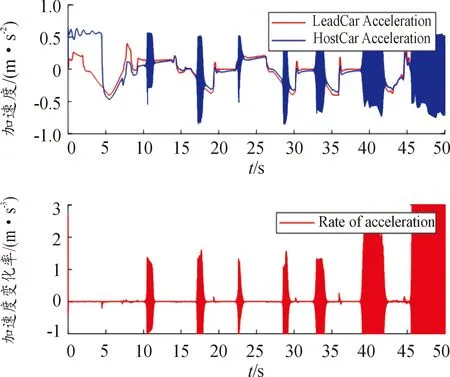
图10 未考虑j的加速度及加速度变化率曲线

图11 考虑j的加速度及加速度变化率曲线
4 结论
1) 通过模型预测控制理论设计的控制器能实现纵向舒适性跟车。
2) 运动学模型中是否考虑自车加速度变化率对纵向跟车的舒适性有着不同的影响,故对于是否考虑自车加速度变化率进行了对比分析,结果表明:考虑自车加速度变化率会有更好的舒适性。
3) 由于前车加速度对于自车的舒适性有一定的影响,故采取跟踪不同行驶状态下的目标车辆,结果表明:目标车辆无论是匀速还是变速,本文所设计的控制器都能满足舒适性的要求。
4) 进行的仿真试验不仅证明理论正确,而且为今后的实车验证提供了依据。
5) 只进行了仿真验证,希望今后能将所设计的控制器用于实车,更好地证明所设计的控制器可以实现舒适性跟车。
