汽车悬架参数实测载荷谱识别方法
2022-02-08邹喜红陈袁莉袁冬梅支川银
邹喜红,陈袁莉,袁冬梅,支川银,向 刚
(1.重庆理工大学 汽车零部件先进制造技术教育部重点实验室, 重庆 400054;2.重庆清研理工汽车检测服务有限公司, 重庆 400000)
0 引言
汽车悬架系统是车轮和车身之间的连接装置,它能将施加在车轮上的力与力矩从路面传递至车辆车身,且有缓冲、减振和导向的作用。作为车辆行驶系统的重要组成部分,悬架对车辆的乘坐舒适性和驾驶安全性起着至关重要的作用[1-2]。汽车的簧上和簧下质量、轮胎刚度、减震器阻尼系数和弹簧刚度等参数是悬架设计和分析的关键参数,但其中有些参数难以直接获取,因此准确地获取和识别汽车悬架参数十分必要。
国内外研究人员在车辆悬架参数的获取和识别方面已经做了不少研究。张慧杰等[3]在传感器坐标系下建立了7自由度整车动力学方程,基于最小二乘估计的递推算法为汽车悬架参数在线识别提供了新方法。曹志伟[4]通过四通道激振器分别给轮胎施加正弦激励信号,迫使悬架系统振动,并利用采集的车轴和车体的加速度信号,依据共振原理识别车辆的悬架刚度、阻尼比等参数。Zhao等[5]建立了重型卡车的3自由度客舱系统线性模型,在对加速度功率谱密度进行曲线拟合的基础上,建立了其阻尼参数识别数学模型,通过试验结果表明该方法有较高的精确度。为解决传统线性及非线性悬架系统参数辨识中的不足,李翠梅等[6]依据最小二乘法原理,提出了通过基于系统离散化模型对简单悬架系统进行识别参数,而基于系统输入输出数据识别方法则对于复杂系统模型适用。
现有研究基本都是通过仿真测试或台架试验进行汽车悬架参数识别,少有采用汽车实际行驶工况载荷数据进行识别和验证,因此,本文提出基于实测载荷谱汽车悬架参数识别方法。结合悬架振动系统动力学,组建了载荷谱测试系统,采集并分析了某试验场典型路面匀速行驶载荷谱。结合1/4悬架模型和最小二乘法,提出了递推最小二乘法悬架参数识别方法,并进行了验证。在此基础上,结合采集和分析后的实际行驶载荷谱,对悬架参数进行了识别,并进行了误差分析及结果验证。
1 实际行驶载荷谱采集与分析
与悬架参数识别息息相关的数据主要有簧上和簧下质量及振加速度、速度、位移、悬架位移等。簧上和簧下质量可以直接获取,重点需要对簧上和簧下振动加速度和悬架相对位移进行采集,然后对振动加速度载荷谱进行两次积分运算分别得到速度载荷谱和位移载荷谱。根据实际采集的簧上、簧下垂向加速度信号进行频域积分再计算以获取相对位移信号,与实测悬架相对位移信号进行误差分析,选取误差最小的截止频率积分结果进行后续悬架参数识别。
1.1 载荷谱采集
路面对行驶车辆的激励大多是频率在50 Hz以下的振动信号[7],为保证测量信号的精确性,采用0~400 Hz频率测量范围的电容式加速度传感器采集垂向加速度信号,其具有良好的频响特性和较好的信噪比等特点。通过拉线式位移传感器获取悬架相对位移信号,该传感器工作原理为通过改变拉线的长度来测量位移距离,然后将其转换为事先已标定的电信号。
信号采集位置需要综合考虑:信号采集点可以更真实地体现被测部件在车辆实际行驶时受到的振动情况;采集位置布置走线与行驶车辆的各运动部分不发生干涉;信号采集点对试验场路面激励的灵敏度能够符合要求,并能改善信噪比。结合上述采集位置选取原则和车辆振动模型,此次载荷谱采集通道及位置如表1所示。

表1 采集通道及位置
在国内某试验场进行实车载荷谱采集,本次载荷谱采集的路况选取主要基于以下原则:所选路段能反映该试验场的典型路面特征;为获取相对平稳的实测载荷谱,选取的工况为匀速行驶;为便于对比验证,所选路段的路面不平度有明显差异。因此,选取高速环道、综合路和异响路3种典型路面作为好路、综合路和坏路的代表,分别进行车速为90、50和20 km/h的匀速行驶,循环采集次数为3次,采用驾驶员变换驾驶,以此消除人为驾驶习惯造成的信号测量误差。通过组建采集系统对CAN信号、加速度信号和位移信号等进行了同步采集,综合路左后轮簧上加速度、簧下加速度和悬架相对位移实测信号如图1所示。
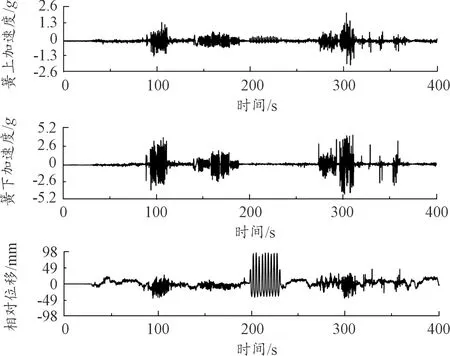
图1 左后轮实测信号曲线
1.2 速度和位移载荷谱获取与验证
在频域内对预处理后的簧上、簧下垂向加速度信号进行一次积分运算获取速度信号,其再次积分获取位移信号。频域积分首先通过傅里叶变换将加速度时域信号转换为频域信号,其次在频域内进行频域积分运算,再将频域积分结果通过傅里叶逆变换转化为时域信号。该积分方法已被广泛运用于振动信号的处理[8-9]。
因为不可避免信号截断泄露,所以频域积分会出现计算误差,而低频段是造成误差的主要原因,因此选取不同的低截止频率加速度信号进行频域积分,获得积分相对位移X(t)是2次积分得到的簧上垂直位移和簧下垂直位移之差,再与实际采集的悬架相对位移对比。引入以下评价指标对误差进行定量分析:标准平均峰值误差(Erp)反映积分信号波形与实测信号波形最大范围的重合度;平均最大相对误差(Err)反映积分信号的局部最大误差;平方和误差(Ersp)反映积分信号与实测信号能量的差值[10-11]。
(1)
式中:N为采样点数;S(t)为实测悬架位移信号。
式(1)误差计算分析结果如表2所示。因此,选取误差最小的0.5~150 Hz截止频率积分结果进行汽车悬架参数识别。
2 悬架系统建模
真实的车辆悬架模型其实是一个非线性系统,但依据泰勒展开式,在忽略高阶项的基础上,其能够在某平衡点较小的周围区域内线性化,这是识别车辆悬架系统参数的关键数学依据。
2.1 1/4悬架模型
悬挂质量分配系数:
(2)
式中:py为绕横轴y回转半径;a、b为车身质量部分的质心至前、后轴的距离。根据企业提供的相关数据,计算得到ε值约为1.031。
当ε接近1时,车辆前、后悬架的垂直方向运动可以看作是相互独立的,于是可以将车辆悬架简化为1/4悬架系统模型,如图2所示[12]。本文主要研究车辆悬架簧上、簧下质量受到的垂直振动,因此重点参数为悬架弹簧刚度K和减振器阻尼系数C;并且AlexandruC指出如果轮胎阻尼系数非常小,则在悬架系统中可以忽略不计[13],因此本文未考虑轮胎阻尼系数。
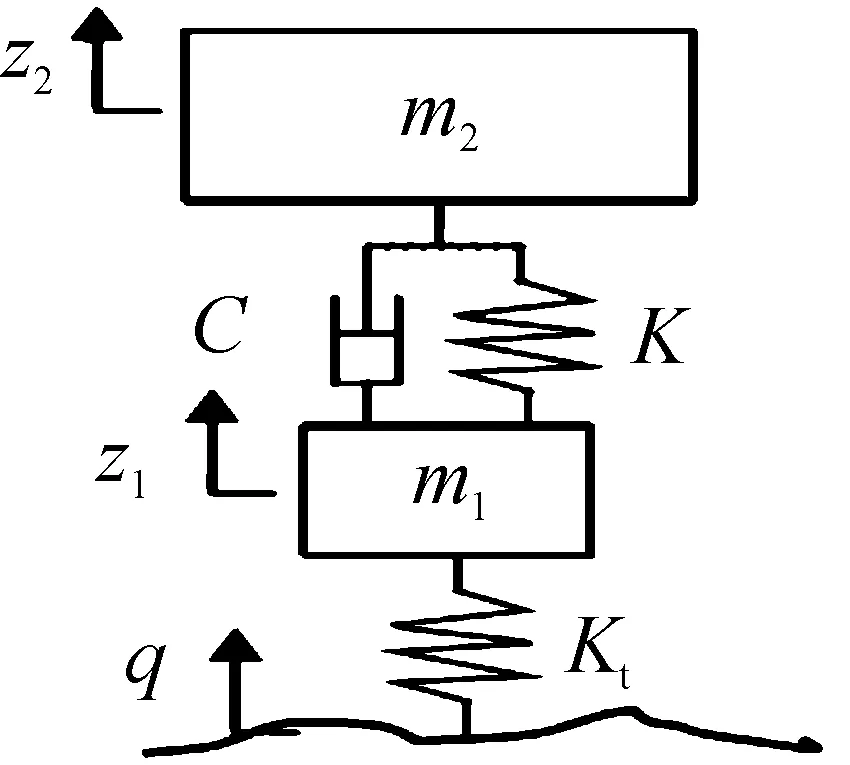
图2 1/4悬架系统模型示意图
图2中:m2:簧上质量;m1:簧下质量;z2:簧上垂直位移;z1:簧下垂直位移;q:路面不平度函数;K:悬架弹簧刚度;C:减振器阻尼系数;Kt:轮胎刚度。
2.2 运动微分方程
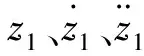
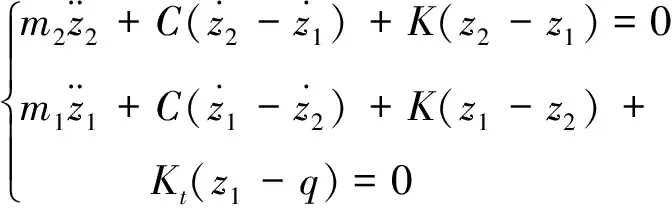
(3)
本次试验车辆前悬架为麦弗逊式悬架,后悬架为扭力梁式悬架,根据实际测量和企业提供的悬架系统部分参数如表3所示,接下来将对悬架弹簧刚度K和减振器阻尼系数C进行识别。

表3 实车悬架系统部分参数
3 参数识别方法与验证
3.1 递推最小二乘法识别方法
近年系统参数识别主流的方法包含最小二乘法、卡尔曼滤波法、极大似然估计法等。最小二乘法作为最基本的识别方法,具有可靠性高、求解方法优良等优点,常常被应用于线性及非线性系统识别中[16-17]。采用最小二乘法识别参考悬架弹簧刚度和减震器阻尼系数,具体思路如下:
将式(3)改写为式(4)所示:
(4)
将式(4)改写成最小二乘法一般形式:
(5)
式中:z(k)为输出变量即悬架系统中的簧上加速度,Φ(k)为输入变量即簧上和簧下位移、速度,θ为未知参数模型即悬架弹簧刚度和减震器阻尼系数,e(k)为噪声。
(6)
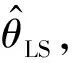
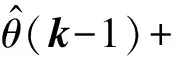
递推最小二乘算法方程为:
(7)
式中:P(k)为对称矩阵;K(k)为增益矩阵。
(8)
递推算法结束的条件如式(8)所示,当σ为适当小的数时,表明所有参数识别值变化不大时停止计算,运用Matlab编制递推算法进行参数识别的流程,如图3所示[19]。

图3 递推最小二乘法Matlab流程框图
3.2 方法验证
通过设定的悬架仿真模型参数值与识别得到的参数值进行对比来验证识别方法是否可行。首先运用Matlab/Simulink搭建1/4悬架系统仿真模型,如图4所示,设置用于验证的仿真模型参数(如表4所示),输入路面为随机路面不平度函数。模型仿真得到50 s的簧上和簧下位移、速度、加速度,簧上、簧下加速度仿真结果如图5所示。
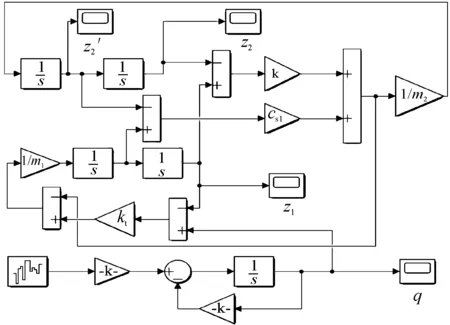
图4 1/4悬架系统仿真模型示意图

表4 悬架仿真模型设定参数值
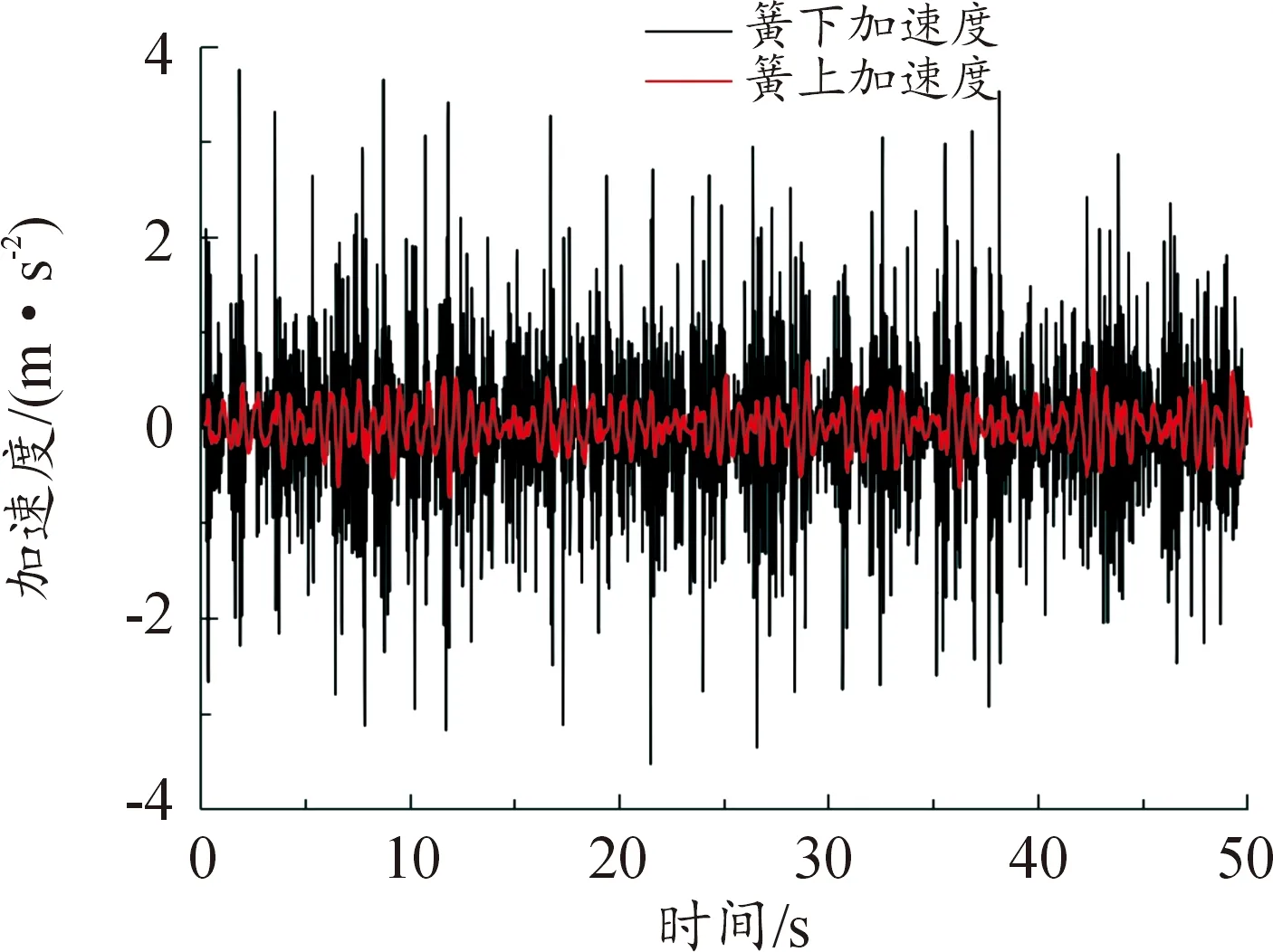
图5 加速度仿真结果曲线
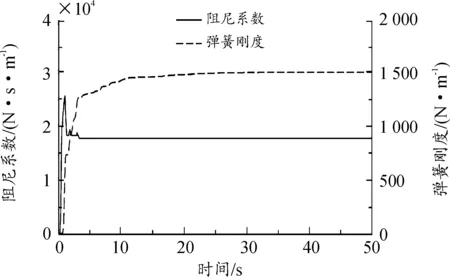
图6 用以验证的悬架弹簧刚度、阻尼系数识别结果曲线
4 实车参数识别与验证
4.1 实车悬架参数识别
根据前文已获取的簧上和簧下的速度、位移及质量参数,基于采集的异响路载荷谱按照图3程序对实车进行悬架弹簧刚度和减振器阻尼系数进行参数识别,异响路实际采集的左前轮簧上、簧下加速度载荷谱如图7所示。实车4个悬架各自的悬架弹簧刚度和减振器阻尼系数识别结果如表5所示,左前悬架识别结果如图8所示。识别结果表明:左前与右前悬架、左后与右后悬架识别出的悬架弹簧刚度和减振器阻尼系数各数值差距较小,符合车辆悬架系统实际情况,具有合理性。

图7 异响路左前轮实测加速度载荷谱曲线

表5 实车悬架参数识别结果

图8 实车左前悬架弹簧刚度、阻尼识别结果曲线
4.2 结果验证
为了验证实车识别结果的准确性,以综合路的路面不平度作为输入,仿真车速与试验场采集时实际车速保持一致,利用仿真簧上、簧下加速度信号与综合路实际采集的加速度载荷谱作图,左前轮仿真与实测簧上、簧下加速度曲线如图9。
从图9可以看出,加速度信号的仿真数据和实测数据总体趋势一致、数值大小总体一致。为了直观且定量地对比结果,进一步计算加速度均方根值及均方根值相对误差。
计算结果表6显示:左前轮仿真与实测的簧上、簧下加速度均方根值相对误差分别为5.0%、3.4%,右前轮仿真与实测的簧上、簧下加速度均方根值相对误差分别为7.6%、2.7%,左后轮仿真与实测的簧上、簧下加速度均方根值相对误差分别为5.1%、1.5%,右后轮仿真与实测的簧上、簧下加速度均方根值相对误差分别为4.7%、4.0%,总体误差较小,从而验证了基于实测载荷谱对汽车悬架参数识别方法的有效性。
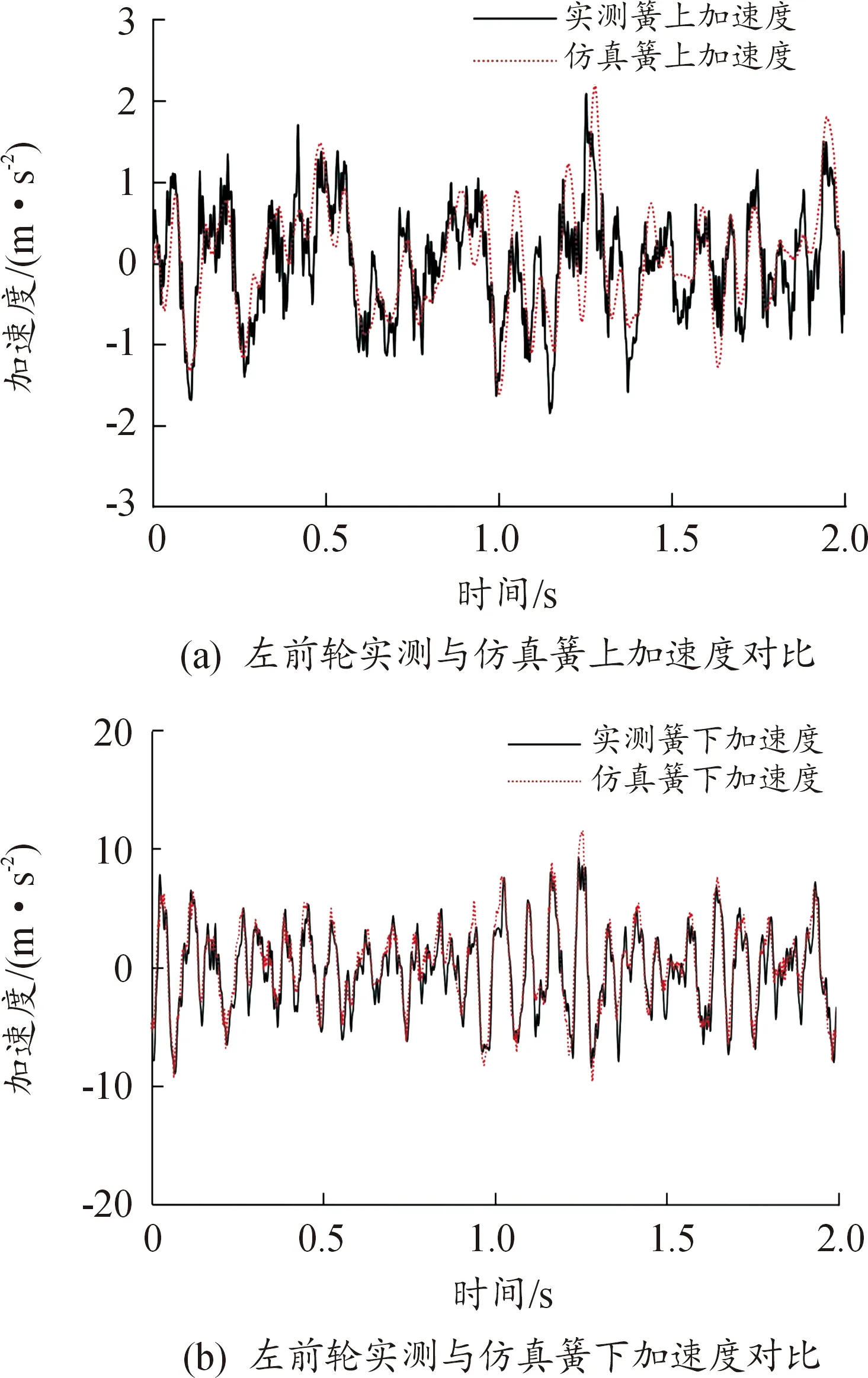
图9 左前轮实测与仿真加速度曲线

表6 仿真与实测加速度均方根值加相对误差
5 结论
1) 组建了车速、振动加速度、悬架位移等载荷谱同步采集系统,通过频域积分获取了速度和位移载荷谱,通过与采集的悬架相对位移载荷谱进行对比发现:截止频率选取在0.5~150 Hz频率范围内积分相对位移误差小。
2) 在建立1/4悬架系统模型的基础上,根据递推最小二乘法进行了悬架刚度和阻尼系数识别,结果表明:识别结果与设定值的相对误差为0.1%,验证了识别方法的可行性。
3) 基于实际采集的异响路载荷谱识别得到了实际车辆的悬架弹簧刚度和减振器阻尼系数,采用综合路路面进行了验证,结果表明:仿真与实测的簧上加速度均方根值相对误差均在8%以内,仿真与实测的簧下加速度均方根值相对误差均在5%以内。
