基于多元振荡黏菌算法的田路分割模型参数优化方法
2022-02-07翟卫欣潘家文兰玉彬吴才聪
翟卫欣,潘家文,兰玉彬,吴才聪
·农业信息与电气技术·
基于多元振荡黏菌算法的田路分割模型参数优化方法
翟卫欣1,2,潘家文1,2,兰玉彬3,4,吴才聪1,2※
(1. 中国农业大学信息与电气工程学院,北京 100083;2. 农业农村部农机作业监测与大数据应用重点实验室, 北京 100083;3. 山东理工大学农业工程与食品科学学院,淄博 255000;4. 国家精准农业航空施药技术国际联合研究中心,广州 510642)
田路分割是农机轨迹语义分割模型的重要任务之一,其目的是将轨迹自动分割为田间作业轨迹和道路行驶轨迹。田路分割模型的参数是影响其分割准确性及精度的关键因素,传统的参数选择方法效率较低且难以获得较好的方案,限制了模型的分割性能。因此,该研究选用基于方向分布的田路分割模型(Field-Road Trajectory Segmentation Based on Direction Distribution,BDFRTS),尝试从参数优化的角度研究模型的性能提升,提出的方法主要包括两个方面,首先建立了一种基于元启发式算法(Metaheuristic Algorithms,MA)的田路分割模型参数优化解决方案;其次,在黏菌算法(Slime Mould Algorithm,SMA)的基础上提出了一种改进的多元振荡黏菌算法(Multiplex Oscillation Slime Mould Algorithm,MOSMA)求解参数优化方案以更好地提高模型的分割性能。MOSMA分别提出一种动态引导策略与多元振荡策略强化了黏菌的振荡收缩反应及细胞质的流动过程,进而增强了算法的优化能力。为验证所提参数优化方法的有效性,将博创联动提供的中国农机在2021年9 月底—10月中下旬进行水稻收割的作业轨迹作为数据集开展试验。试验结果表明,该研究所提方法有效地提升了田路分割模型的准确性和性能。MOSMA-BDFRTS分割模型在10组高密度轨迹中的平均准确率相比网格搜索田路分割模型、粒子群田路分割模型分别提高了25和28个百分点;在10组低密度轨迹中分割的平均准确率分别提高了17和14个百分点。该研究可为田路分割技术提供合理的性能优化方案,也为农业机械运动轨迹分割技术的效率研究提供参考依据。
模型;参数优化;田路分割;黏菌算法;动态引导;多元振荡
0 引 言
田路分割的目的是将农业机械上搭载的全球导航卫星系统终端中记录的时空轨迹数据分割成一系列田间作业-道路行驶的子轨迹[1]。作为农业领域时空轨迹处理问题重要研究内容,田路分割可从大数据角度为精准农业相关课题的深入研究与科学管理提供有力支撑[2],如乡村路网构建[3]、田间作业效率评估[4-5]、农机跨区调度管理[6]、农机作业路径规划[7-9]等。
现有的田路分割方法大多利用边界信息来区分农田轨迹和道路轨迹[10-11],然而,由于边界信息不够可靠导致农田的实际边界难以自动标定,使得此类方法的适用性较差[12]。为了解决这个问题,Chen等[13]利用机器学习技术[14]提出一种基于方向分布的田路分割模型,通过聚合内含相同空间特征的轨迹点实现了农田轨迹与道路轨迹的自动分割。模型的参数反映了其样本学习的成效,同时也是影响其分割性能的关键因素,对参数进行优化可以使模型更好地表达轨迹的特征。然而,真实场景中的天气、地形、采样频率、作业任务等因素都会影响轨迹变化,使轨迹空间特征呈现多元化现象,为模型参数的选择带来巨大的挑战。目前,国内外学者对田路分割问题鲜有研究,现有模型在参数标定方面仍处于较原始的阶段,无法充分发挥模型性能,导致分割效果仍不够理想,如何通过参数优化提高模型准确性与性能成为了本文研究的首要问题。
参数优化是指从一个巨大受限解决方案空间找到最佳参数结构,本质上是函数优化问题。由于不同参数的交互影响,使分割模型参数优化问题呈现出非线性、多峰值的复杂数学特性,用传统的方法求解费时耗力,选出的参数结构质量差,限制了模型的性能。近年来,元启发式算法[15-18]因其鲁棒性强、不依赖于目标问题的梯度信息等优势被国内外众多学者用于求解复杂非线性问题,相比传统方法在更短时间内取得了相同或更好的结果[19-23]。张良安等[24]利用粒子群算法(Particle Swarm Algorithm,PSO)对四足激光除草机器人腿部结构的相关参数进行优化,有效地提高了续航能力。Ding等[25]利用PSO算法提出了一种用于植物虚拟生长模型的参数优化方法。Jamei等[26]提出了一种基于鲸鱼优化算法的人工神经网络模型,增强了模型在地表蒸散指数预测任务中的准确性。上述研究表明,利用元启发式算法优化参数能够有效提升相关算法模型解决实际任务的能力。
本文主要从参数优化的角度研究田路分割模型的性能提升问题。首先通过确定编码方案和适应度函数将参数优化问题转化为单目标优化问题,进而提出了一种基于元启发式算法的田路分割模型参数优化解决方案,旨在利用元启发式算法作为优化工具求解方案,在解空间内自动搜索模型的最优参数结构,进而实现准确、快速的田路分割。由于传统的元启发式算法易陷入局部收敛,训练出来的参数难以为田路分割模型确定合适的空间特征来准确地分割农机轨迹。为提高模型分割效率,对基本黏菌算法(Slime Mould Algorithm,SMA)改进提出了一种多元振荡黏菌算法(Multiplex Oscillation Slime Mould Algorithm,MOSMA)用以求解模型的参数优化问题。为验证所提方法有效性,在真实的农机作业轨迹数据集上进行了实证研究。
1 材料与方法
1.1 基于方向分布的田路分割模型
本文选用基于方向分布的田路分割模型(Field-Road Trajectory Segmentation Based on Direction Distribution,BDFRTS)作为所提方法的优化实例。农机田间作业的轨迹点呈现两种特点:1)田内轨迹因车速较低呈现聚集状态,使得单位空间内的轨迹点密度较高。2)连续的作业轨迹带的行驶方向角度近似平行分布且相反。分割方法利用上述特点对轨迹进行分割,如图1所示,主要包括三个步骤:1)为提供高质量的轨迹数据进行分割,对轨迹噪声点进行平滑处理,对重复轨迹点进行过滤。2)使用基于密度的聚类算法[27]分割轨迹,并分配不同的语义标签。3)针对步骤2)错误分类情况(“农田”预测为“道路”或“道路”预测为“农田”),采用基于方向分布的推理算法进行纠正。具体地说,在基于轨迹簇的田转路推理规则中,利用簇中轨迹点在区域方向分布的差异性将错误分类的假“田”点转换为“路”;轨迹带生成与轨迹带噪声过滤先将具有相同作业操作且连续的轨迹点连接为轨迹带,再处理轨迹的噪声点;在基于轨迹带的路转田推理规则中,利用同一块农田中轨迹带彼此平行关系将假“路”点转换为“田”。
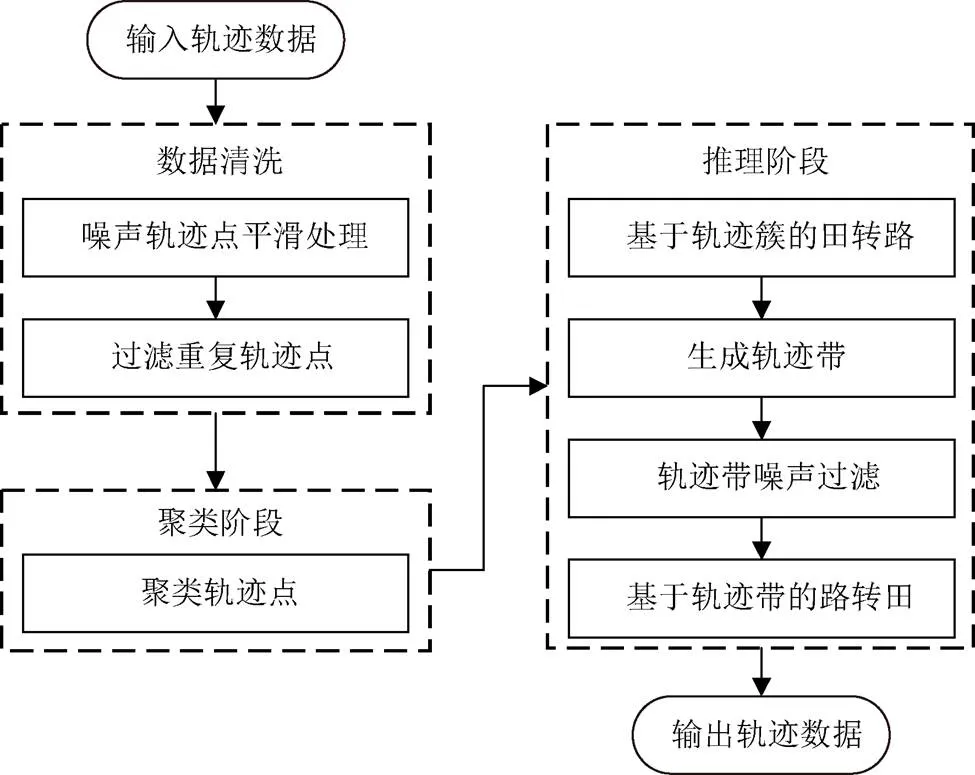
图1 基于方向分布的田路分割模型
1.2 基于MOSMA的田路分割参数优化方法
田路分割模型能够在轨迹空间中构建一种超平面来分离不同类别的轨迹,为实现其分割性能的最大化,需对模型参数进行优化来提高超平面的泛化能力。本文首先针对田路分割任务参数优化问题的需求,通过确定问题的优化目标、编码方案,适应度函数建立起参数优化模型作为优化方案;然后以最大化分割准确率为优化目标,提出一种改进的多元振荡黏菌算法来求解方案。整体优化方法的基本思想是:首先将模型的参数向量抽象为搜索个体,在轨迹数据的驱动下运行田路分割模型,并以分割结果作为搜索个体在解空间内适应情况的评价指标,然后按照优化算法的计算规则利用适应度来引导个体的搜索方向,同时更新搜索个体所对应参数向量的信息,最后将更新后的参数向量重新代入分割模型中计算适应度,如此反复,直到找到最佳参数结构或满足算法终止条件。
1.2.1 编码方案
设田路分割模型含有个参数,所有参数都被缩放到[]区域中形成一个统一的解空间,其中与分别表示解空间的上界与下界。解空间中的每个搜索个体都表示一项维度为的参数向量,其中每个元素都对应模型的一个参数,其值可根据模型实例设置为二进制或浮点数,为算法种群个体的数目。本文采用随机初始化的方式构建算法的种群。
1.2.2 适应度函数
适应度函数代表搜索个体在解空间的有效信息,同时也是评价参数向量泛化能力的重要准则。田路分割任务属于二分类问题,利用机器学习中的三种基于时间的性能指标查准率(Precision),查全率(Recall)与调和平均值(F1-score)评估其分类精度。
参数优化的目标是通过持续调整每个参数向量的值来获得泛化效果最好的超平面,进而最大限度地提高轨迹的分割效果。本文以最大化分割精准度为优化目标,将参数优化问题转换为单目标优化问题。每个搜索代理使用F1-score作为其对应参数向量的适用性标准,最优搜索代理适应度应满足于最大调和平均值。
1.2.3 基本黏菌算法
黏菌优化算法是由Li等[28]于2020年提出的一类元启发式算法,其灵感来源于黏菌的觅食行为和形态变化,数学模型可以表达为
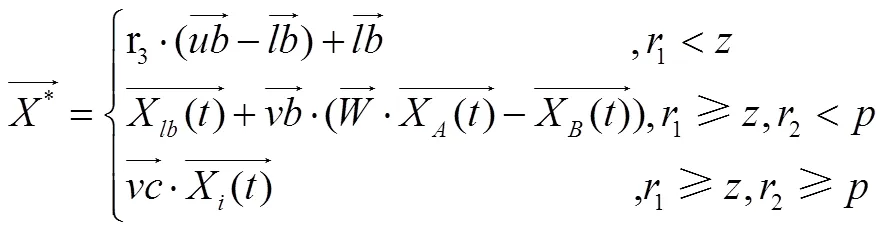
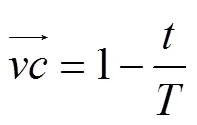
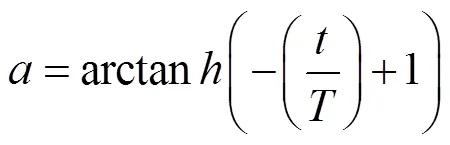
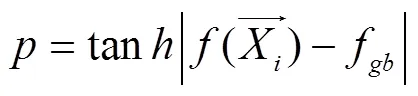

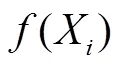
1.2.4 改进的多元振荡黏菌算法
元启发式算法的性能取决于其全局搜索能力、局部搜索能力及两者之间的协调平衡。本文选用的SMA全局搜索能力较差,无法在田路分割模型参数约束范围内充分搜索。为满足模型的参数优化性能要求,本研究在SMA的基础上,提出一种改进的多元振荡黏菌算法求解田路分割模型参数优化问题。
1)动态引导策略

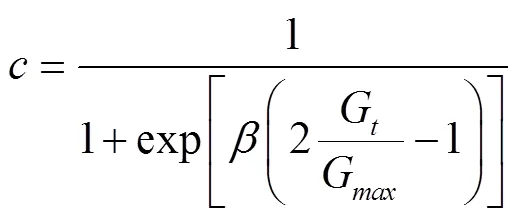
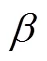
2)多元振荡策略
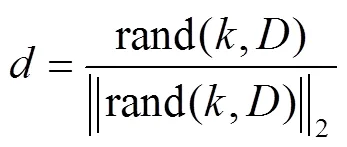
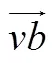

1.2.5 计算流程
基于MOSMA参数优化方法计算步骤可概括为:
1)数据处理:清洗轨迹数据(包括平滑噪声点和过滤重复点),并划分为训练集和验证集。
2)参数设定与算法初始化:设置算法相关的参数,包括种群数目,参数维度、参数上界与下界、最大迭代次数等,初始化算法种群的位置。
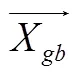
4)参数优化:以适应度为引导信息更新算法的参数,种群中的每个搜索个体分别通过式(1)、动态引导策略与多元振荡策略更新位置信息,最后更新迭代次数1。
2 结果与分析
2.1 试验设置
为评估基于MOSMA的参数优化方法对田路分割模型计算效率的提升效果,本文采用真实的谷物联合收割机在2021年9月底—10月中下旬进行水稻收割的作业轨迹展开试验,所有轨迹数据均由博创联动公司提供。地理空间上分布于中国的多个省级行政区,具体包括青海省、陕西省、四川省、内蒙古、河南省、湖北省、安徽省、江西省、江苏省。为验证参数优化方法的普适性,试验选用了两组搭载不同型号定位终端的农机轨迹数据集。为有效地区分两组数据集,根据定位终端的采样频率不同及其之间的相对关系,定义了{低密度数据集,高密度数据集}语言集合。其中高密度数据集中相邻轨迹点的时间间隔为3 s,低密度数据集相邻轨迹点的时间间隔为5 s。每组数据集均包括10个不同的轨迹样本,分别由D1~D10和S1~S10表示,详细数据见表1。
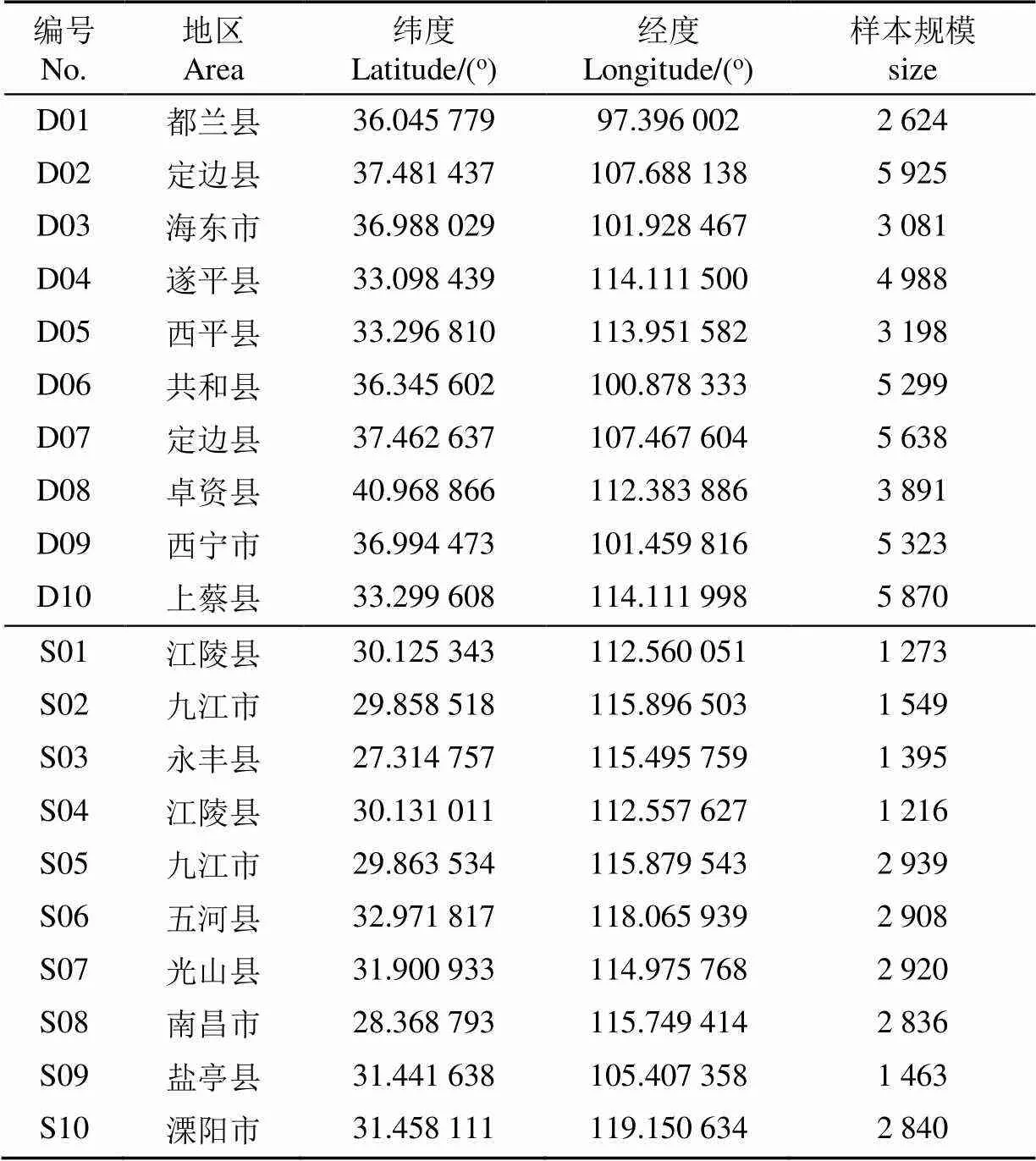
表1 农机运动轨迹数据基本信息
注:纬度、经度取自轨迹样本的起始点;样本规模是指一幅轨迹所包含的轨迹点数目。
Note: Latitude and longitude are extracted from the first point of the trajectory sample; the size refers to trajectory point number of a trajectory.
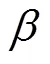
2.2 模型对比试验分析
表2表示MOSMA-BDFRTS和GS-BDFRTS两种模型在高密度轨迹数据集中的试验结果对比,可以看出,MOSMA-BDFRTS的计算结果均优于GS-BDFRTS和PSO-BDFRTS。在10组高密度轨迹中,MOSMA-BDFRTS的平均准确率相比GS-BDFRTS,PSO-BDFRTS分别提高了25和28个百分点。其中,MOSMA-BDFRTS在D03、D09等样本中取得了明显地提升,在农田作业轨迹的F1-score值相比GS-BDFRTS分别提升了3和12个百分点,相比PSO-BDFRTS分别提升了3和4个百分点;在道路行驶轨迹的F1-score值比GS-BDFRTS分别提高了34和69个百分点,相PSOPSO-BDFRTS分别提高了35和50个百分点。相比GS-BDFRTS和PSO-BDFRTS,MOSMA-BDFRTS在高密度轨迹样本的分割识别中的农田作业轨迹的F1-score值均提高了6个百分点;在道路行驶轨迹的F1-score值平均提升了43和50个百分点。PSO-BDFRTS在D06、D08、D09的F1-score值优于GS-BDFRTS,但在其他样本中均低于GS-BDFRTS,表明PSO易陷入局部最优,优化能力较差,而本文所提的MOSMA能够摆脱局部最优,在全局范围内为BDFRTS搜索到更好的参数结构。
表3展现了不同方法在低密度轨迹数据集中的试验结果。MOSMA-BDFRTS分割模型在10组低密度轨迹中分割的平均准确率相比GS-BDFRTS,PSO-BDFRTS模型分别提高了17和14个百分点。相比GS-BDFRTS和PSO-BDFRTS,MOSMA-BDFRTS在所有的低密度轨迹样本分割识别中的农田作业轨迹F1-score值平均提高了17和9个百分点,在道路行驶轨迹的F1-score值平均提升了17和19个百分点。试验结果表明,MOSMA-BDFRTS在低密度轨迹数据中能够取得更好的分割结果。此外,MOSMA-BDFRTS在S01、S08两项轨迹样本中相比GS-BDFRTS分别获得了66与34个百分点的显著提升;与PSO-BDFRTS比较,MOSMA-BDFRTS在S02、S04轨迹样本有明显的提升,其农田作业轨迹的分割准确率提升了17与1个百分点,道路行驶轨迹的准确率分别提升了36与31个百分点,而在其他轨迹样本中也都取得了更好的优化效果,说明MOSMA的性能优于PSO。表4给出了不同田路分割模型参数选择的执行时间,可以看出,本文所提方法的计算开销明显低于GS,略低于PSO。轨迹样本的数据量越大,GS计算所需的时间就越久,此时使用MOSMA的计算收益就越大,因此MOSMA在处理大规模轨迹数据时更具优势。综上,基于MOSMA的参数优化方法能够在更短的时间内确定田路分割模型的最优参数结构,提升模型分割准确率,具有较好的适应性和鲁棒性。
2.3 收敛性分析
图2展现了三种模型在四组轨迹样本参数训练过程中的收敛曲线,GS不具备元启发式算法中常规意义上的迭代次数概念,为便于比较,将搜索次数按比例转换成迭代次数。从图2中可以看出,相比GS-BDFRTS和PSO-BDFRTS,MOSMA-BDFRTS能够在较少的迭代次数内收敛于最优参数结构,证明了算法优化性能的优越性。从图2整体来看,MOSMA-BDFRTS收敛曲线的变化呈单调上升趋势,且在更少的迭代次数内取到最优值,说明算法有较好的收敛能力和优化速度。
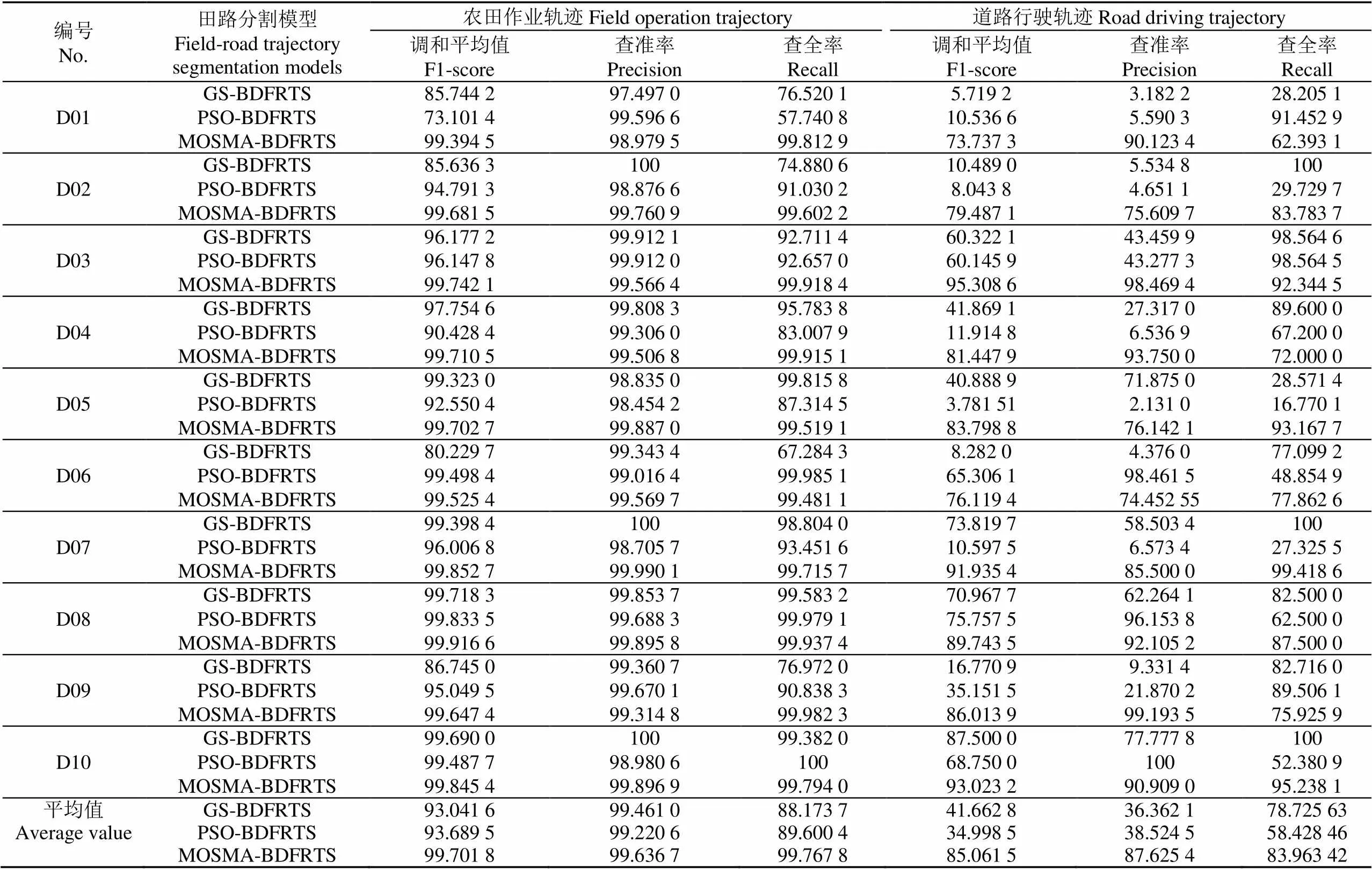
表2 不同田路分割模型在高密度轨迹的分割结果对比
注:GS-BDFRTS、PSO-BDFRTS和MOSMA-BDFRTS表示基于方向分布的田路分割模型分别配置网格搜索法、粒子群算法和多元振荡黏菌算法,下同。
Note: GS-BDFRTS, PSO-BDFRTS and MOSMA-BDFRTS are represent the field-road trajectory segmentation model configures grid search method, particle swarm algorithm and multiplex oscillation slime mould algorithm, respectively, same below.

表3 不同田路分割模型在低密度轨迹的分割结果对比
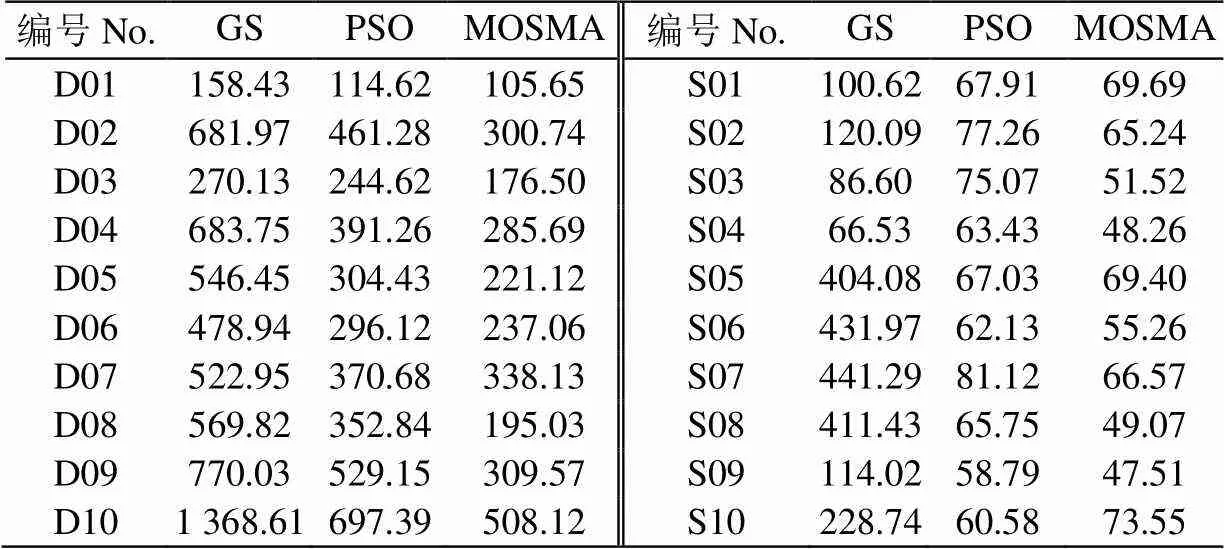
表4 不同参数选择方法的耗时对比
注:GS、PSO和MOSMA分别表示使用网格搜索法、粒子群算法和多元振荡黏菌算法选择模型的参数。
Note: GS, PSO and MOSMA refers the use grid search method, particle swarm algorithm and multiplex oscillation slime mould algorithm to select parameters for the model.
2.4 参数优化效果对比
为更加直观地分析本文所提方法的优化效果,图3展现了部分轨迹样本用GS-BDFRTS与MOSMA- BDFRTS进行分割的结果。由表2和表3可知,MOSMA-BDFRTS在D01、D02、S01、S02样本中取得了明显地提升,在农田作业轨迹的F1-score值分别提升了13、14、9与14个百分点;在道路行驶轨迹的F1-score值分别比GS-BDFRTS提高了68、69、66与5个百分点。从图3展现的轨迹分割图像可以清晰地看出,经MOSMA-BDFRTS分割后的轨迹分类在相应的地图背景下的准确率更高,说明本文所提方法能够提供更优越的分割结果。

a. 轨迹样本D01a. Trajectory sample D01b. 轨迹样本D02b. Trajectory sample D02c. 轨迹样本S01c. Trajectory sample S01d. 轨迹样本S02d. Trajectory sample S02

图3 不同田路分割模型的分割结果
3 结 论
为了提升田路分割模型的性能,本研究从参数优化的角度切入,提出了一种面向田路分割模型的参数优化方法。该方法以最大化分割准确率为优化目标,为田路分割模型建立了一种通用的参数优化方案,其能够使用元启发式算法求解优化方案来自动标定模型的参数结构。为了解决传统元启发式算法因性能低下求解方案困难的问题,提出了一种多元振荡黏菌算法,该算法提出了动态引导策略与多元振荡策略提升了优化性能。在20组不同密度的农机作业轨迹数据中开展试验,结果表明,基于多元振荡黏菌算法的参数优化方法能有效提升田路分割模型的性能。在分割结果方面,多元振荡黏菌算法优化的田路分割模型相比网格搜索法和粒子群算法优化的田路分割模型在高密度轨迹数据中的分割准确率分别提高了25和28个百分点;在低密度轨迹数据中的分割准确率分别提高了17和14个百分点。从分割效果和平均处理时间等指标综合来看,基于多元振荡黏菌算法的参数优化方法能够有效地提升田路分割模型的性能。本文所提方法为田路分割模型提供了一种通用的参数优化解决方案,可直接应用于其他类型的模型实例中。
[1] 肖敬,刘卉,魏学礼,等. 基于时空立方体的农机运动轨迹分割方法[J]. 江苏农业科学,2018,46(20):244-247.
Xiao Jing, Liu Hui, Wei Xueli, et al. Segmentation of agricultural machinery trajectories based on space-time cube[J]. Jiangsu Agricultural Sciences, 2018, 46(20): 244-247. (in Chinese with English abstract)
[2] 孙忠富,杜克明,郑飞翔,等. 大数据在智慧农业中研究与应用展望[J]. 中国农业科技导报,2013,15(6):63-71.
Sun Zhongfu, Du Kengming, Zheng Feixiang, et al. Perspectives of research and application of big data on smart agriculture[J]. Journal of Agricultural Science and Technology, 2013, 15(6): 63-71. (in Chinese with English abstract)
[3] 冯晓莉,王永兴,仇宝云. 基于混合狼群算法参数优选的泵站群运行优化[J]. 农业工程学报,2020,36(3):30-36.
Feng Xiaoli, Wang Yongxing, Chou Baoyun. Optimization of pumping station group operation based on optimized parameters using hybrid wolf pack algorithm[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(3): 30-36. (in Chinese with English abstract)
[4] 王培,孟志军,尹彦鑫,等. 基于农机空间运行轨迹的作业状态自动识别试验[J]. 农业工程学报,2015,31(3):56-61.
Wang Pei, Meng Zhijun, Yin Yanxin, et al. Automatic recognition algorithm of field operation status based on spatial track of agricultural machinery and corresponding experiment[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(3): 56-61. (in Chinese with English abstract)
[5] 刘卉,孟志军,王培,等. 基于农机空间轨迹的作业面积的缓冲区算法[J]. 农业工程学报,2015,31(7):180-184.
Liu Hui, Meng Zhijun, Wang Pei, et al. Buffer algorithms for operation area measurement based on global navigation satellite system trajectories of agricultural machinery[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(7): 180-184. (in Chinese with English abstract)
[6] 吴才聪,蔡亚平,罗梦佳,等. 基于时间窗的农机资源时空调度模型[J]. 农业机械学报,2013,44(5):237-241,231.
Wu Caicong, Cai Yaping, Luo Mengjia, et al. Time-windows based temporal and spatial scheduling model for agricultural machinery resources[J]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(5): 237-241, 231. (in Chinese with English abstract)
[7] 翟卫欣,王东旭,陈智博,等. 无人驾驶农机自主作业路径规划方法[J]. 农业工程学报,2021,37(16):1-7.
Zhai Weixin, Wang Dongxu, Chen Zhibo, et al. Autonomous operation path planning method for unmanned agricultural machinery[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2021, 37(16): 1-7. (in Chinese with English abstract)
[8] 翟志强,王秀倩,王亮,等. 面向主从跟随协同作业的导航路径规划方法[J]. 农业机械学报,2021,52(S1):542-547.
Zhai Zhiqiang, Wang Xiuqian, Wang Liang, et al. Collaborative path planning for autonomous agricultural machinery of master-slave cooperation[J]. Transactions of the Chinese Society for Agricultural Machinery, 2021, 52(S1): 542-547. (in Chinese with English abstract)
[9] 姚竟发,刘静,张璠,等. 基于多普勒与贪心策略的农机作业路径优化研究[J]. 中国农机化学报,2020,41(4):130-137.
Yao Jingfa, Liu Jing, Zhang Fan, et al. Optimization of agricultural machinery operation path based on doppler and greedy strategy[J]. Journal of Chinese Agricultural Mechanization, 2020, 41(4): 130-137. (in Chinese with English abstract)
[10] Kortenbruck D, Griepentrog H W, Paraforos D S. Machine operation profiles generated from ISO 11783 communication data[J]. Computers and Electronics in Agriculture, 2017, 140: 227-236.
[11] Hanke S, Trösken L, Frerichs L. Development and parameterization of an object-oriented model for describing agricultural process steps[J]. Landtechnik, 2018, 73(2): 22-36.
[12] Kilic T, Zezza A, Carletto C, et al. Missing (ness) in action: selectivity bias in GPS-based land area measurements[J]. World Development, 2017, 92: 143-157.
[13] Chen Y, Zhang X, Wu C, et al. Field-road trajectory segmentation for agricultural machinery based on direction distribution[J]. Computers and Electronics in Agriculture, 2021, 186: 106180.
[14] Bertolini M, Mezzogori D, Neroni M, et al. Machine Learning for industrial applications: A comprehensive literature review[J]. Expert Systems with Applications, 2021, 175: 114820.
[15] Ding X, Zheng M, Zheng X. The application of genetic algorithm in land use optimization research: A review[J]. Land, 2021, 10(5): 526.
[16] Houssein E H, Gad A G, Hussain K, et al. Major advances in particle swarm optimization: theory, analysis, and application[J]. Swarm and Evolutionary Computation, 2021, 63: 100868.
[17] Yu X, Xu W, Li C. Opposition-based learning grey wolf optimizer for global optimization[J]. Knowledge-Based Systems, 2021, 226: 107139.
[18] Dhiman G, Singh K K, Soni M, et al. MOSOA: A new multi-objective seagull optimization algorithm[J]. Expert Systems with Applications, 2021, 167: 114150.
[19] Tam N T, Hung T H, Binh H T T. A decomposition-based multi-objective optimization approach for balancing the energy consumption of wireless sensor networks[J]. Applied Soft Computing, 2021, 107: 107365.
[20] Dhal P, Azad C. A multi-objective feature selection method using newton’s law based pso with gwo[J]. Applied Soft Computing, 2021, 107: 107394.
[21] D’Angelo G, Palmieri F. GGA: A modified genetic algorithm with gradient-based local search for solving constrained optimization problems[J]. Information Sciences, 2021, 547: 136-162.
[22] Kapoor K, Rani S, Kumar M, et al. Hybrid local phase quantization and grey wolf optimization based SVM for finger vein recognition[J]. Multimedia Tools and Applications, 2021, 80(10): 15233-15271.
[23] Xu L, Hou L, Zhu Z, et al. Mid-term prediction of electrical energy consumption for crude oil pipelines using a hybrid algorithm of support vector machine and genetic algorithm[J]. Energy, 2021, 222: 119955.
[24] 张良安,唐锴,赵永杰,等. 四足激光除草机器人腿部结构参数优化[J]. 农业工程学报,2020,36(2):7-15.
Zhang Liang’an, Tang Kai, Zhao Yongjie, et al. Optimization of leg structure parameter of quadruped laser weeding robot[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(2): 7-15. (in Chinese with English abstract)
[25] Ding W L, Zhao Y L, Xin W T, et al. Parameter extraction method of virtual plant growth model based on Improved Particle Swarm Optimization[J]. Computers and Electronics in Agriculture, 2021, 191: 106470.
[26] Jamei M, Elbeltagi A, Maroufpoor S, et al. Combined terrestrial evapotranspiration index prediction using a hybrid artificial intelligence paradigm integrated with relief algorithm-based feature selection[J]. Computers and Electronics in Agriculture, 2022, 193: 106687.
[27] Ester M, Kriegel H P, Sander J, et al. A density-based algorithm for discovering clusters in large spatial databases with noise[C]// Proceedings of the Second International Conference on Knowledge Discovery and Data Mining. Portland, America: ACM, 1996: 226-231.
[28] Li S, Chen H, Wang M, et al. Slime mould algorithm: A new method for stochastic optimization[J]. Future Generation Computer Systems, 2020, 111: 300-323.
[29] 王鹏新,齐璇,李俐,等. 基于粒子群优化投影寻踪的玉米单产估测[J]. 农业工程学报,2019,35(13):145-153.
Wang Pengxin, Qi Xuan, Li Li, et al. Estimation of maize yield based on projection pursuit with particle swarm optimization[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(13): 145-153. (in Chinese with English abstract)
Parameter optimization of field-road trajectory segmentation model using multiplex oscillation slime mould algorithm
Zhai Weixin1,2, Pan Jiawen1,2, Lan Yubin3,4, Wu Caicong1,2※
(1.,,100083,;2.,,100083,;3.,,255000,;4.,510642,)
Field-Road Trajectory Segmentation (FRTS) is one of the important tasks of agricultural machinery. A sequence of field-road segments of a trajectory can be automatically divided for the big data in precision agriculture. The parameter of the FRTS model can also determine the segmentation accuracy and precision. However, the traditional parameter selection cannot obtain the superior solution, limiting the segmentation performance of the model. Therefore, this study aims to investigate the performance improvement of the FRTS model from the perspective of parameter optimization. Two aspects were mainly contained as follows. Firstly, the metaheuristic algorithms were used to determine the parameter configuration of the model. The classification accuracy was considered as an objective to transform the parameter into a single-objective optimization. Specifically, the parameter structure of the model was abstracted as the searched individual of the optimization. The reasonable fitness function was set, according to the metrics of FRTS evaluation. Then, the fitness was used to evaluate the search of the individual in the solution space. The location of the searched individual was also continuously adjusted, according to the calculation rules of the optimization. As such, the global optimal parameter structure was achieved to converge. Secondly, a Multiplex Oscillation Slime Mould Algorithm (MOSMA) was proposed to realize the parameter optimization with the nonlinear characteristics and multiple locally optimal solutions. A dynamic guidance strategy was also established to adaptively change the individual movement for the better exploitation capability of the model, according to the search process of the population. Then, a strategy (called multivariate oscillation) was proposed to improve the segmentation performance and exploration capability of the model. Different search paths were utilized to produce multiple oscillations before the individual moves, and the priori rule was then to evaluate the qualities of paths. As such, the path with the highest quality was selected to move. The synergy of the two strategies enhanced the optimization capability of the model. Dynamic guidance and a multiplex oscillation strategy enhanced the oscillation contraction patterns of the slime mould and the process of the cytoplasm flows, thereby improving the optimization performance of the model. The experiments were also performed on real agricultural trajectory datasets with different sampling frequencies. A comparison was then made with the Grid Search (GS) and Particle Swarm Optimization (PSO) to validate the effectiveness of the model. The experiment results show that the new optimization effectively improved the accuracy and performance of the FRTS model using direction distribution (BDFRTS). The average accuracy of the MOSMA-BDFRTS on high-density trajectory data was increased by 25 percentage points and 28 percentage points compared with GS-BDFRTS and PSO-BDFRTS. MOSMA-BDFRTS achieved more competitive results on low-density trajectory data, whose average accuracy of segmentation was improved by 17 percentage points and 14 percentage points compared with GS-BDFRTS and PSO-BDFRTS. The proposed method provides a generalized parameter optimization solution for field-road trajectory segmentation models, and it can be applied directly to other types of model instances. The study also provides a reference for the research of the agricultural machinery movement trajectory segmentation technology.
model; parameter optimization; field-road trajectory segmentation; slime mould algorithm; dynamic guidance; multiplex oscillation
10.11975/j.issn.1002-6819.2022.18.019
S126
A
1002-6819(2022)-18-0176-08
翟卫欣,潘家文,兰玉彬,等. 基于多元振荡黏菌算法的田路分割模型参数优化方法[J]. 农业工程学报,2022,38(18):176-183.doi:10.11975/j.issn.1002-6819.2022.18.019 http://www.tcsae.org
Zhai Weixin, Pan Jiawen, Lan Yubin, et al. Parameter optimization of field-road trajectory segmentation model using multiplex oscillation slime mould algorithm[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2022, 38(18): 176-183. (in Chinese with English abstract) doi:10.11975/j.issn.1002-6819.2022.18.019 http://www.tcsae.org
2022-06-26
2022-09-12
国家精准农业应用项目(JZNYYY001);北京市科技计划项目(Z201100008020008);中国科协科技智库青年人才计划项目(20220615ZZ07110141)
翟卫欣,博士,副教授,博士生导师,研究方向为时空大数据、地图学与地理信息系统、智能农机等。Email:zhaiweixin@cau.edu.cn
吴才聪,博士,教授,博士生导师,研究方向为农机导航与位置服务等。Email:wucc@cau.edu.cn
中国农业工程学会会员:翟卫欣(E041201339S)
