变截面悬臂空心圆柱的冲击动力特性

杨杰， 张慧， 李爱纯， 高天

(兰州交通大学土木工程学院， 兰州 730070)

变截面悬臂空心圆柱因其良好的力学特性，多年来一直是工程中最常用的结构之一。目前，有关研究已取得较多进展。张宏生等[1]从挠度微分方程出发，应用传递矩阵法得到了阶梯柱模型整体稳定性欧拉临界力求解控制方程的表达式。贺丽平等[2]在针对变截面门式刚架柱的稳定性计算中, 分别对大头截面参数和小头截面参数进行探讨, 提出了稳定系数φ′b的简化公式。卞敬玲等[3]在三维退化梁单元的基础上引入几何非线性，导出了计算任意变截面压杆稳定问题的有限元列式。练章华等[4]基于弹塑性力学理论建立了实际井况下油管柱屈曲行为分析的有限元力学模型，对管柱屈曲行为的影响程度开展了研究。吴莹等[5]导出了变圆截面弹性悬臂柱的后屈曲控制方程，解决了强非线性边值问题。Lee等[6]在研究等体积变截面悬臂柱的大挠度荷载时考虑剪切变形的影响，导出了控制柱屈曲形状的几何非线性微分方程。Bakker[7]从能量原理着手，结合逆解思想和试函数方法，导出了均布荷载作用下悬臂柱弯剪屈曲的近似计算公式。惠宽堂等[8]通过系数拟合对弯剪型屈曲的临界荷载计算公式予以修正，得到弯剪型悬臂柱的屈曲临界荷载计算公式。赵钦等[9]综合考虑悬臂柱的剪切与弯曲变形，得到了等截面与变截面形式下弯矩放大系数的表达式。

Borodin等[10]对非弹性悬臂柱体系进行了抗震分析，将非弹性系统的震动分析归结为准静态问题。Darbandi等[11]研究了受分布轴力作用的变截面柱的静稳定性，得到了计算屈曲载荷和相应的模态振型的封闭解。Lee等[12]利用直接积分法导出了轴压荷载作用下轴功能梯度悬臂柱的横向自由振动问题的控制微分方程。潘旦光等[13]基于直接模态摄动法的基本原理建立一种求解变截面Timoshenko梁动力特性的近似分析方法，将梁的特征方程的微分方程组转化为代数方程组从而进行求解。禹金云[14]通过函数变换法给出了变截面杆在自由纵向振动情形下的部分精确解。崔凯等[15]基于Abaqus有限元对不同冲击能量和冲击位置下格构式钢柱的动态响应进行有限元分析，表明悬臂试件在冲击位置较低时的冲击力时程曲线发展趋势与两端简支试件相似,变形破坏由剪切效应控制。陈玉骥等[16]研究了突加荷载作用下，变截面空心柱在考虑了惯性力后的动力特性，给出了塑性铰位置参数和悬臂端中点加速度在不同影响参数下的变化规律。

现有悬臂变截面空心柱的研究主要集中在静力稳定性与振动稳定性两大类，较少涉及冲击荷载作用下的动力特性研究。然而，在工程中，变截面悬臂空心圆柱有可能受到冲击荷载作用，因此，有必要针对其冲击响应展开研究。现拟从准静态极限分析与冲击动力学理论入手，对其在冲击荷载作用下的动力特性展开研究，分析不利工况产生的条件，以便提高其使用可靠性。

1 本构关系与准静态极限分析

图1为受冲击荷载F作用的变截面悬臂空心圆柱。D0与D2分别为悬臂端(以字母c表示)与固定端(以字母f表示)的截面外径；H为构件跨度；z为悬臂端到固定端的距离(高度)。定义荷载位置参数μ，并以μH表示荷载F的作用位置到悬臂端的距离；z为悬臂端到固定端的距离(高度)。

图1 受冲击荷载作用的变截面悬臂空心圆柱Fig.1 Cantilever hollow cylinder with variable cross-section under impact load

为简化其动力响应分析，本文中悬臂柱的本构关系采用理想钢塑性材料模型。

由弹塑性力学可知，薄壁圆环截面的塑性极限弯矩为

(1)

式(1)中：d、D与td为截面内径、外径与壁厚；σy为材料屈服应力。

显然，Mp为直径的二次式。因此，根据量纲分析，设任意截面的塑性极限弯矩为

(2)

式(2)中：Mp0、Mp1、Mp2分别为悬臂端、跨中和固定端的截面塑性极限弯矩。

根据准静态极限分析，设区间z>μH，上杆段任一截面的静态极限荷载为

(3)

式(3)中：Fx0、Fx1和Fx2分别为悬臂端、跨中和固定端的截面在x方向的静态极限荷载。

当变截面悬臂空心圆柱受到冲击荷载作用时，其会绕柱的某一截面发生转动，即在该截面产生塑性铰。显然，塑性铰出现的位置情况有两种：①塑性铰位于固定端；②塑性铰位于柱中。因此，现将根据塑性铰出现的位置情况，对其冲击动力特性展开分类研究。此外，因工程中常用的变截面悬臂空心圆柱常分为等厚度柱与变厚度柱两类，故亦分类讨论。

2 塑性铰位于固定端

图2为悬臂柱塑性铰位于固定端的运动模式。vc(t)为悬臂端中点的速度；Rf为固定端的水平支反力；Mp2为固定端的截面塑性极限弯矩。

图2 塑性铰位于固定端的悬臂柱转动模式Fig.2 Rotation mode of cantilever cylinder with plastic hinge at the fixed end

2.1 等厚度柱的冲击动力特性

等厚度柱的厚度为td，悬臂端、固定端的截面内径分别为d0和d2，d(z)表示高度为z时空心柱截面的内径，材料密度为ρ。为分析等厚度柱在该情形下的冲击响应，可根据冲击动力学，先对其在x方向运用动量定理，有

(4)

积分得

(5)

再应用动量矩定理，有

F(1-μ)H-Mp2

(6)

积分得

(7)

联立式(5)和式(7)得

(8)

由式(8)第二式可得悬臂端中点的加速度，则任一截面的加速度为

(9)

由结构力学可知，截面剪力V(z)与分布惯性力存在以下关系，即

(10)

积分可得

(11)

根据弯矩与剪力的微分关系可得

(12)

2.2 变厚度柱的冲击动力特性

变厚度柱的内径为d，悬臂端、固定端的截面厚度分别为t0、t2，t(z)表示高度为z时空心柱截面的壁厚，材料密度为ρ。与2.1节同理可得

(13)

积分得

(14)

式(14)中：ζ=3(d+2t0)t0+(d+4t0)(t2-t0)+(t2-t0)2，ξ=20(d+2t0)t0+5(d+4t0)(t2-t0)+4(t2-t0)2。

3 塑性铰位于柱中

图3表示悬臂柱塑性铰位于柱中的运动模式。定义塑性铰位置参数λ，并以λH表示塑性铰位置到悬臂端的距离；Fxλ为塑性铰截面的静态极限荷载，Mp为相应的塑性极限弯矩。

图3 塑性铰位于柱中的悬臂柱转动模式Fig.3 Rotation mode of cantilever cylinder with plastic hinge in the cylinder

由2.1节的分析可知，塑性铰在悬臂柱中产生的条件为F>Fx2且μ≤μxc。但真实情况是：当F稍微大于Fx2时，即使μ≤μxc，塑性铰仍会在固定端产生。事实上，由图3便可看出，只有当F>Fxλ时，悬臂柱才会发生转动。因此，塑性铰在柱中产生的条件应为：F>Fxλ>Fx2与μ≤μxc。

3.1 等厚度柱的冲击动力特性

分别运用动量定理与动量矩定理，有

(15)

对式(15)第一式积分，得悬臂端加速度为

(16)

将式(16)代入式(15)中第二式，积分得

(d2-d0)λ3-2[μ(d2-d0)-d0]λ2-6μd0λ=0

(17)

式(17)为塑性铰位置参数λ的控制方程。当d2=d0时，变截面柱变为等截面柱。若μ≠0，式(17)变为λ=3μ，故有：当μ<1/3时，等截面柱的塑性铰在柱中产生，即μ<λ<1，且λ=3μ；当μ≥1/3时，塑性铰在固定端产生，即λ=1。

3.2 变厚度柱的冲击动力特性

分别运用动量定理与动量矩定理，有

(18)

对式(18)第一式积分，得悬臂端加速度为

(19)

式(19)中：ζ=(t2-t0)2λ3+(d+4t0)(t2-t0)λ2+3(d+2t0)t0λ。

将式(19)代入式(18)第二式，积分得

6(t2-t0)2λ4+5(d+4t0)(t2-t0)λ3-

10(t2-t0)2μλ3+10(d+2t0)t0λ2-

10(d+4t0)(t2-t0)μλ2-30(d+2t0)t0μλ=0

(20)

式(20)即为λ的控制方程。当t2=t0时，变截面柱变为等截面柱。

4 算例

4.1 等厚度变截面悬臂空心圆柱算例

算例参数：H=5 000 mm，d0=200 mm，d2=300 mm，td=12 mm，ρ=7.85×103kg/m3，σy=240 MPa，F=1.855×105N，μ=0.2。算例离散模型如图4所示。

根据参数算得Fx2=1.195×105N，μxc=0.357 1，Fxλ=1.853 3×105N。满足F>Fxλ>Fx2与μ<μxc，故塑性铰将在柱中产生。将λ与ac的计算结果列于表1。

图4 变截面悬臂空心圆柱离散模型Fig.4 Discrete model of cantilever hollow cylinder with variable cross-section

表1 等厚度悬臂柱的动力参数对比Table 1 Comparison of dynamic parameters of cantilever cylinder with constant thickness

由表1可知，塑性铰位置参数λ与悬臂端加速度ac的本文解与数值解吻合良好。

保持F不变，改变μ，绘得μ-λ关系曲线、μ-ac关系曲线、λ-ac关系曲线分别见图5～图7，并予以有限元验证。

由图5可知，塑性铰位置参数λ随荷载位置参数μ的增大而增大，且二者关系几乎为线性；当μ超过临界荷载位置参数μxc=0.357 1时，塑性铰发生在固定端，即有λ=1。

由图6可知，悬臂端加速度ac随着荷载位置参数μ的增大而减小：当μ<0.15时，ac下降较快；当μ>0.15时，ac下降趋势逐渐放缓。

由图7可知，悬臂端加速度ac随塑性铰位置参数λ的增大而减小：当λ<0.4时，ac下降很快；当λ>0.4时，ac下降趋势逐渐放缓。

4.2 变截面变厚度悬臂空心圆柱算例

算例参数：H=5 000 mm，d=300 mm，t0=10 mm，t2=20 mm，ρ=7.85×103kg/m3，σy=240 MPa，F=4.205×105N，μ=0.2。

图5 等厚度变截面悬臂空心圆柱μ-λ关系曲线Fig.5 μ-λ relation curve of cantilever hollow cylinder with equal thickness and variable section

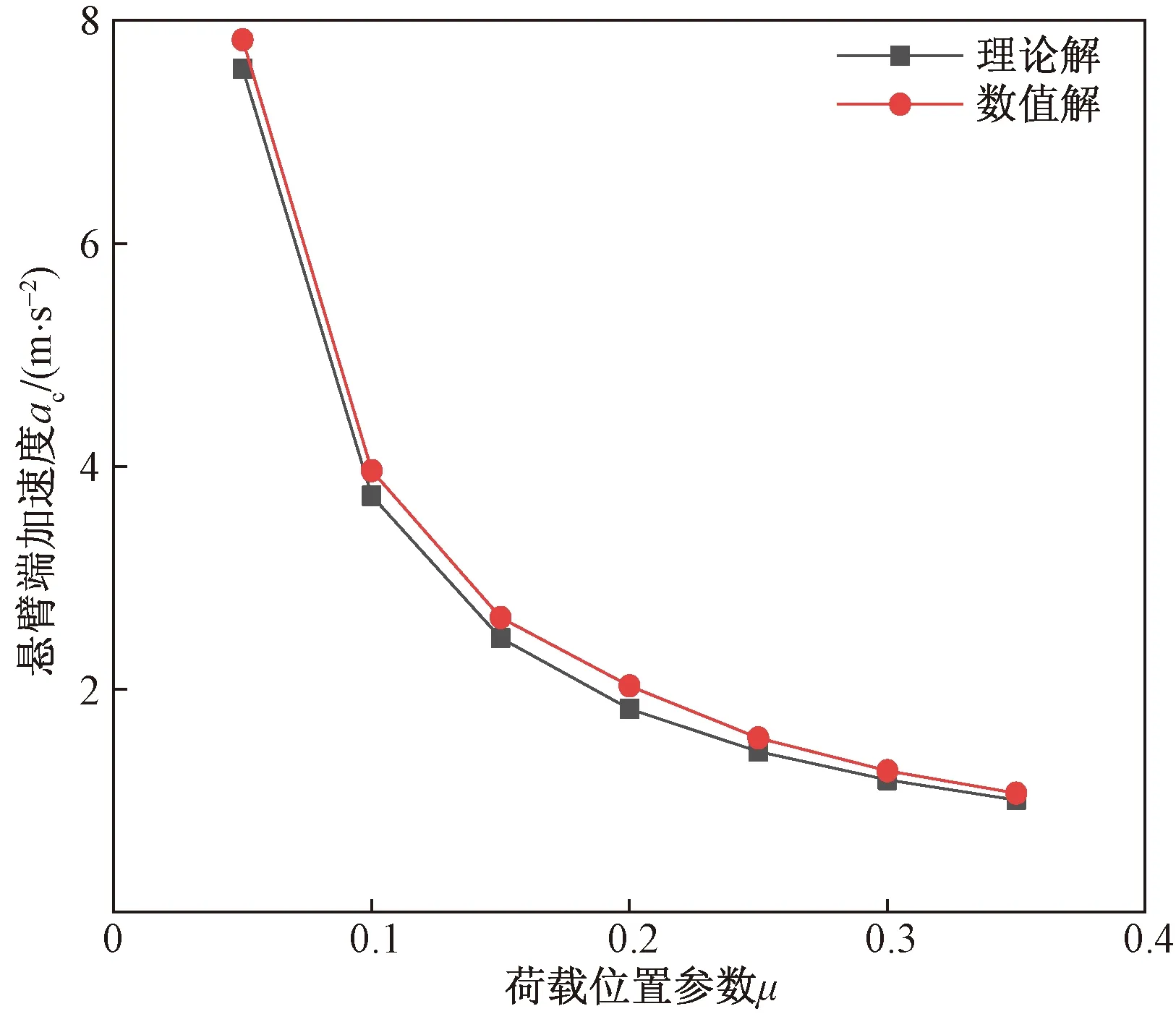
图6 等厚度变截面悬臂空心圆柱μ-ac关系曲线Fig.6 μ-ac relation curve of cantilever hollow cylinder with equal thickness and variable section

图7 等厚度变截面悬臂空心圆柱λ-ac关系曲线Fig.7 λ-ac relation curve of cantilever hollow cylinder with equal thickness and variable section

根据参数算得Fx2=2.460 8×105N，μxc=0.378 6，Fxλ=4.202 9×105N，满足条件F>Fxλ>Fx2与μ<μxc，故塑性铰位于柱中。将λ与ac的计算结果列于表2。

由表2可知，塑性铰位置参数λ与悬臂端加速度ac的本文理论解与有限元解吻合良好。

保持F不变，改变μ，绘得μ-λ曲线、μ-ac曲线、λ-ac曲线分别见图8～图10。

表2 变厚度悬臂柱的动力参数对比Table 2 Comparison of dynamic parameters of cantilever cylinder with variable thickness

图8 变截面变厚度悬臂空心圆柱μ-λ关系曲线Fig.8 μ-λ relation curve of cantilever hollow cylinder with variable section and thickness

图9 变截面变厚度悬臂空心圆柱μ-ac关系曲线Fig.9 μ-ac relation curve of cantilever hollow cylinder with variable section and thickness

由图8可知，μ-λ曲线近似成线性，当μ超过μxc=0.378 6时，塑性铰发生在固定端，即有λ=1。

由图9可知，ac随μ的增大而减小：当μ<0.15时，ac下降快；当μ>0.15时，ac下降趋势逐渐放缓。

由图10可知，ac随λ的增大而减小：当λ<0.4时，ac下降快；当λ>0.4时，ac下降趋势逐渐放缓。

图10 变截面变厚度悬臂空心圆柱λ-ac关系曲线Fig.10 λ-ac relation curve of cantilever hollow cylinder with variable section and thickness

5 结论

以准静态极限分析与冲击动力学为理论基础，分析了冲击荷载作用在不同位置时，等厚度、变厚度变截面悬臂空心圆柱的动力特性，得到以下结论：

(1)当F>Fx2且μ>μxc时，变截面悬臂空心圆柱将在固定端产生塑性铰。

(2)当F>Fxλ>Fx2且μ≤μxc时，变截面悬臂空心圆柱将在柱中产生塑性铰；塑性铰位置参数λ只与荷载位置参数μ有关，即λ可由控制方程求得。

(3)μ-λ关系曲线表明：λ随μ的增大而增大，二者关系几乎为线性；当μ超过μxc时，塑性铰在固定端产生。

(4)μ-ac关系曲线表明：ac随μ的增大而逐渐减小，前期下降较快，后期下降趋势渐缓。

(5)λ-ac关系曲线的变化规律与μ-ac关系曲线的规律类似。