基于未确知测度理论的山区管道地质灾害风险评估

陈利琼， 曾志强， 张开

(西南石油大学石油与天然气工程学院， 成都 610500)

西南山区管道作为中国能源进口四大通道之一，其沿线地形地貌复杂，地质灾害频发，故管道的设计、施工、运行和维护世界罕见[1]。在管道运营过程中，西南管道公司管理的油气管道跨越三大阶梯地形[2]，70%以上位于山区，沿线山高谷底，河流与山脉相间排列，因滑坡、水毁、崩塌、泥石流等地质灾害造成管道事故层出不穷。据统计，2019年西南地区的重庆、四川、贵州等地区共发生地质灾害1 046起，占中国地质灾害数量的17%，其中滑坡在地质灾害中占比最大，是中国地质灾害较严重的区域。直到2021年底，西南地区的地质灾害防治依然十分严峻，地质灾害破坏力大、突发性强，给山区管道的风险管控带来了极大挑战。但风险评价是管控的前提，为确保山区管道的安全运营，如何全面、准确、定量地对管道进行风险评价已成为各管道公司关注的重点。

目前，关于管道地质灾害风险评价方法的研究，因山区管道地质灾害复杂性和不确定性较大，考虑的因素多，单靠一种方法不能够系统、准确地对管道进行风险评价。为了综合考虑，许多学者采用定性评价、半定量评价、定量评价中两种或三种相结合的方法进行风险评价。其中，潘禹臣等[3]结合沿线的地质环境，建立区域内地质灾害风险评价指标体系，通过灰色关联分析计算权重，利用加权信息量模型完成对中缅天然气管道沿线的地质灾害风险评估。杨惠元[4]分析了滑坡对天然气管道的危害，建立了中缅管线地区定量和半定量结合的安全风险评估指标模型，运用层次分析法量化确定指标评估等级，结合风险矩阵对管道进行风险评估。冼国栋等[5]基于GIS技术构建了区域管道地质灾害风险评价模型，利用栅格计算器获取各指标的权重，并根据计算的风险值确定管道的风险等级。以上研究更多的利用常用权重计算方法将指标因素进行处理，将复杂问题按照权重排序决策；但山区管道受地形等客观条件限制，很多因素的状态都不容易确定，数据的测量和监测较多，很容易造成数据收集不全面，大部分采用定性方法研究，使得在指标赋值和人为打分上存在较大的主观性，造成结果的不准确。而未确知测度理论能够在数据不全面的情况下，利用不确定测度函数解决客观信息不全面的问题，并对未知系统的事物进行定量描述，从而降低人为主观选择，提高评估的准确性。

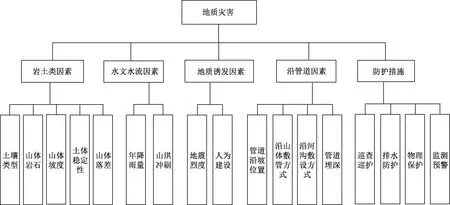
图1 山区管道地质灾害指标体系Fig.1 Index system of pipeline geological disaster in mountainous area

对于未确知测度理论，已广泛运用于多个领域，如城市燃气管道风险评价[6]、边坡稳定性评价[7]，崩塌危险性评价[8]，采空区地面沉降风险评价[9]等；虽然该理论也较少运用于管道风险的研究，但未在此基础上建立符合管道风险等级的评估准则，不能够很好地结合管道指标评价等级判断风险等级。

为此，现应用未确知测度理论定量的描述指标因素，结合层次分析法计算权重，并根据山区管道地质灾害的风险等级判定管道风险，使得山区管道风险评估结果更加准确。

1 建立山区管道地质灾害指标体系

为了建立符合西南山区油气管道地质灾害的指标体系，通过现场调研、综合专家意见以及结合《油气管道地质灾害风险管理技术规范》等相关文献的研究[10-13]，建立科学的山区管道指标体系。该指标体系主要从岩土类因素、水文水流因素、地质诱发因素、沿管道因素和防护措施5方面进行风险评价分析。该指标体系包括5个二级指标和17个三级指标，如图1所示。

2 未确知测度理论介绍

对某研究对象进行评价时，评价对象空间是由所研究对象的全部评价因素组成的集合空间，记作I。该空间集合内的m个评价因素，用I1，I2，…，Im表示，则评价对象空间可写作：I={I1，I2，…，Im}。对任意评价因素Ii有n个评价指标，则评价因素Ii的评价指标空间X是由X1，X2，…，Xn这n个指标构成的集合，即X={X1，X2，…，Xn}。若xij表示第i个评价因素Ii关于指标Xj(j=1,2,…,n)的测量值，则xi可表示一个n维向量：xi={xi1，xi2，…，xin}。设xij有P个评价等级C1，C2，…，Cp，评价空间记为C，C={C1，C2，…，Cp}。对第k个评价等级的安全程度大于第k+1级，记为Ck>Ck+1，若C1>C2>…>Cp，则称{C1，C2，…，Cp}是评价空间C的1个有序分割类。

若测量值xij属于第k个评价等级Ck的程度，记uijk=u(xij∈Ck)，且u满足关系式

(1)

式(1)中：i=1,2,…,m;j=1,2,…,n;k=1,2,…,p。

则称u为未确知测度[14]，其中u必须同时满足非负有界性、归一性和可加性。

2.1 构造单指标未确知测度

为了求某评价因素Xi的各指标测度值uijk，构造单指标测度函数u(xij∈Ck)(i=1，2，…，m；j=1，2，…，n；k=1，2，…，p)，则称各指标测度值uijk构成的矩阵(uijk)m×p为单指标测度评价矩阵，表达式为

(2)

2.2 确定未确知测度函数方法

采取应用最广、最简单的直线型未确知测度函数(图2)，其表达式为

(3)

(4)

图2 直线型未确知测度函数图Fig.2 Graph of linear unascertained measure function

2.3 指标权重的确定

因评价指标等级中定性指标较多，为减少人为主观评估的影响，故采用层次分析法计算权重[15]。其流程如下。

2.3.1 建立层次结构模型

根据图1建立的山区管道地质灾害指标体系构建层次结构模型。

2.3.2 构造判断矩阵

在风险评价指标体系基础上，为了量化比较两因素的重要程度，常采用1～9标度法[16]，表1所示。

表1 因素比较标度法及其说明Table 1 Factor comparison scale method and its description

设rij表示本层次两个因素(xi和xj)之比，建立的判断矩阵R为

2.3.3 计算权重

采用和积法求权重W，将矩阵R按列归一化处理，近似作为权重向量。即

(5)

(6)

其次，计算矩阵R的最大特征值λmax，即

(7)

2.3.4 一致性检验

一致性比例CR是检验判断矩阵R是否满足一致性条件的重要标准，其计算公式为

(8)

(9)

式中：CI为一致性指标；RI为平均随机一致性指标；λmax为最大特征值；n为矩阵阶数。表2为平均随机一致性指标RI的取值。

表2 平均随机一致性指标取值Table 2 Average random consistency index values

当一致性比率CR<0.1，则判定矩阵R符合一致性条件；反之，则需对矩阵进行调整，直至满足CR<0.1为止。

2.4 多指标未确知测度

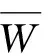
(10)

则uik=(ui1,ui2,…,uip)，为Ii多指标综合测度评价向量。

2.5 建立风险等级识别准则

设多指标综合评价向量u=(k1,k2,…,kp)。根据正态分布的特点，结合置信度识别准则[14]，发现地质灾害下管道处于某风险区间的概率越大，向量u对应的向量值ki就越大，离ki越近的值变化幅度越小，离ki越远的值变化幅度越大。为此，依据山区管道地质灾害的指标因素等级建立风险等级识别准则，如表3为不同风险等级识别准则。

3 指标因素等级划分

根据图1建立的山区管道地质灾害指标体系，三级指标包括4个定量指标和13个定性指标，将每个指标对应分为3个评价等级，对应事件的低概率、中等概率和高概率，表示为C={C1，C2，C3}。采用分级标准量化法[14]对13个定性指标量化处理，按照1-4-7对评价指标分级划分。山区管道地质灾害指标体系评价等级标准如表4所示。

根据2.2节直线型未确知测度函数构建风险评价模型，下面结合定性和定量指标划分的评价等级确定指标函数图形，如图3～图7所示。

表3 风险等级识别准则Table 3 Risk grade identification criteria

表4 山区管道地质灾害指标体系对应的评价等级标准Table 4 Evaluation grade standards corresponding to the geological disaster index system of pipeline in mountainous areas

续表4

图3 地震烈度指标测度函数Fig.3 Measure function of seismic intensity index

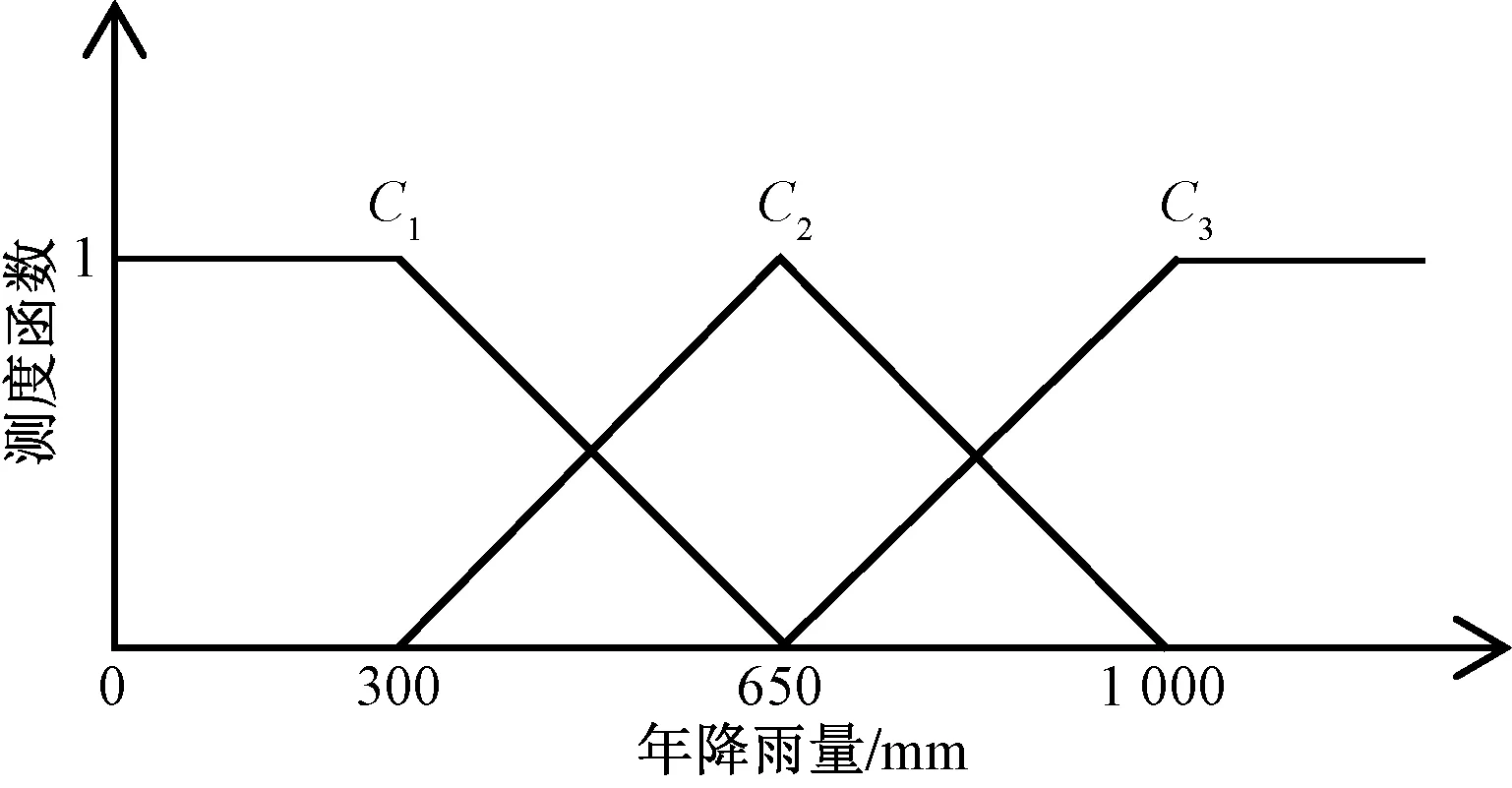
图4 年降雨量指标测度函数Fig.4 Measure function of annual rainfall index

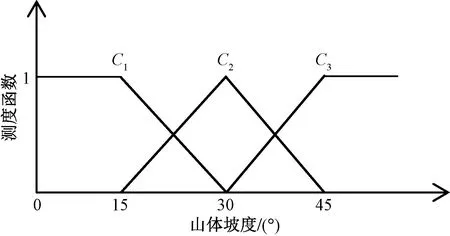
图5 山体坡度指标测度函数Fig.5 Index measure function of mountain slope

图6 埋深指标测度函数Fig.6 Burial depth index measure function

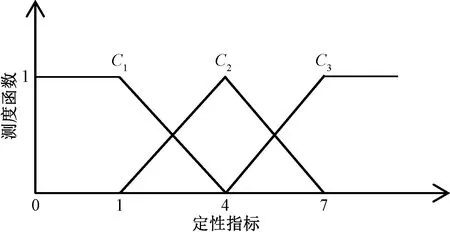
图7 定性指标测度函数Fig.7 Qualitative index measure function

4 应用实例

该管段为西南地区的中贵天然气管线，管段长为2 261 m，经专项排查发现较高地质灾害1处。该区域地形起伏大，山区面积占65%以上，坡度为50°～60°。其中，该区域年降雨量为800～1 100 mm，夏季6—8月降雨量较大，河流较多，均属于长江流域。该区域的土壤是砂粒较小的黄砂土，不是地震频发地段。根据该区域的管理人员了解，由于地形较复杂，管段的监测预警主要依靠人为监测和无人机巡航辅助监测。

根据山区管段的实际情况，确定出各个评价指标的值，如表5所示。

表5 山区管段地质灾害评价指标取值Table 5 Value of geological hazard evaluation index for pipeline section in mountainous area

4.1 单指标评价矩阵确定

将表4的取值代入直线型未确知测度函数图3～图7中，确定各评价因素的单指标评价矩阵分别为

(11)

(12)

(13)

(14)

(15)

4.2 权重确定

根据专家和现场工作人员的意见、管道事故数据分析得出不同评价因素间的重要度比较，如表6～表11所示。

表6 二级指标重要度比较Table 6 Comparison of importance of secondary indicators

表7 岩土类因素指标重要度比较Table 7 Comparison of significance of geotechnical factors

表8 水文水流因素指标重要度比较Table 8 Comparison of importance degree of hydrologic and flow factor indexes

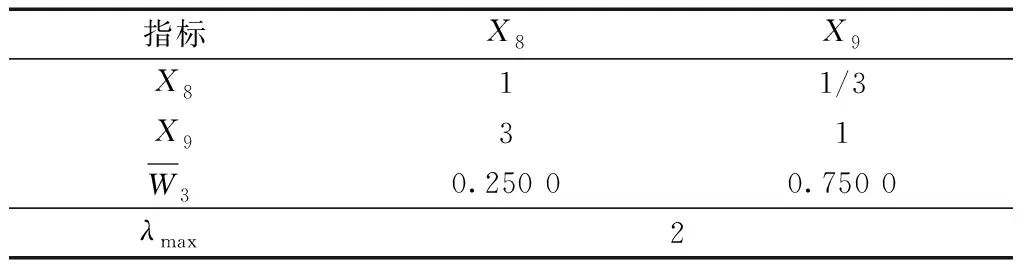
表9 地质诱发因素指标重要度比较Table 9 Comparison of the importance of geological inducing factors index

表10 沿管道因素指标重要度比较Table 10 Comparison of importance of factor along pipelines

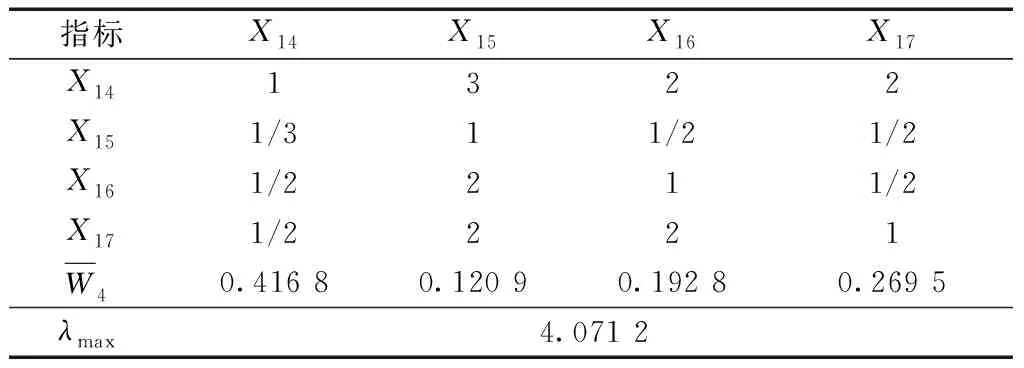
表11 防护措施指标重要度比较Table 11 Comparison of importance of protective measures

4.3 多指标未确知测度确定

由求得的单指标评价矩阵和权重，根据式(10)计算出多指标未确知测度评价向量为

(16)

4.4 风险等级确定

4.5 评价结果

通过对该山区管段各指标因素的取值发现，该区域山体坡度大、山体落差大、年降雨较多、山洪冲刷频繁、管段沿河沟道敷设多、物理保护不全面等情况，使管道失效的概率增大。由于一些指标因素是自然环境形成的，是不可改变的，或者说改变的成本太大，对此不过多考虑；如土壤类型、山体岩石、山体坡度、山体落差、年降雨量等指标因素。为此，主要从人为可改变的因素方面考虑，如规范人为建设后的回填、提高管道埋深、增设管道的预警和预测手段等，通过改变以上因素降低管道风险，提高管道的安全性。

5 结论

(1)结合西南山区特点，建立符合山区管道的地质灾害指标体系，利用未确知测度理论确定各底层指标的未知信息，将各定性指标进行量化处理，对各评价指标因素的发生划分为低概率、中等概率和高概率等级，采用层次分析法计算指标权重，建立了符合山区管道的五级风险等级，为山区管道地质灾害的风险评价提供了新方法。

(2)基于未确知测度理论的山区管道地质灾害风险评价实例分析，与专项排查情况对比后，该评价结果符合实际，说明该方法的科学性和适用性。

(3)相比通过风险矩阵判断管道的风险等级，该方法建立的风险等级，有机的结合未确知测度理论和层次分析法，能准确地判定山区管道地质灾害风险等级。

(4)通过评价结果分析，可从人为可改变的因素来提高管控效率，降低管道事故，确保管道安全。