特高压输电导线直流电场下过冷雨滴碰撞系数
2022-02-06周超孙剑峰
周超, 孙剑峰
(1.华北电力大学,电站能量传递转化与系统教育部重点实验室, 北京 102206;2.华北电力大学,河北省电力机械装备健康维护与失效预防重点实验室, 保定 071003)
输电导线覆冰是过冷却雨滴在低温物体上冻结的一种自然现象。气流中雨滴与导线碰撞的幅度与导线直径的比称为碰撞系数。碰撞系数决定了导线捕获雨滴能力的大小,在冻结系数一定时,碰撞系数越大,导线表面收集的雨滴增多,则覆冰量也越大。碰撞系数是研究覆冰增长的重要参数,其计算准确与否直接决定了覆冰预测的精度及准确性。
中外诸多学者先后对覆冰导线碰撞系数的计算方法进行了探究。Lenhard[1]在1946年对碰撞系数进行了数值解析。Makkonen[2-5]提出了冻结系数的概念及导线结冰时间的相关数值模型,并对大气结冰过程进行了模拟,研究了冰量随大气条件的变化规律。文献[6]中对苏联研究的碰撞系数进行了总结,得出碰撞系数积分式,但由于部分方程无法获得解析式,不能有效地对碰撞系数进行计算。Personne等[7]根据在C.R.Mount观冰站的观测资料得出导线直径为6.25 mm时的碰撞系数经验公式,但该经验公式仅适用于导线直径非常细小的情况,对于较粗导线,该公式误差比较大。中国学者Han等[8]在Makkonen[2-5]的基础上细化并完整推导出了碰撞系数及雨滴冻结系数的具体运算公式,并数值求解得到各种气象参数及导线尺寸下的碰撞系数分布。此后,张志劲等[9]通过数值求解覆冰过程中复合绝缘子外部连续气流场和雨滴运动轨迹,提出一种以区域分割方式数值计算绝缘子表面雨滴碰撞系数的方法,并分析了风速和雨滴中值体积直径(median volume diameter, MVD)对雨滴碰撞系数的影响。此外,相关领域学者们同时较为关注导线覆冰模型[10-13]、雨滴碰撞特性[14-15]、风雨载荷[16-17]、导线气动力特性[18-20]等多种因素对输电线路的影响。
现着重对雨滴碰撞特性进行分析,而碰撞系数是反映碰撞特性的重要表现形式。陈吉等[21]采用欧拉法来建立冰面的碰撞模型,并对不同条件的覆冰碰撞特性进行计算研究。研究表明,碰撞系数受覆冰外形影响明显,并随新月形和翼型覆冰表面质量的增加而减小。黄新波等[22]对圆形、椭圆形、翼形3种典型导线覆冰的碰撞系数仿真。仿真结果表明:相同导线覆冰形状,攻角越大,碰撞系数越高。高晋等[23]对不同种类的导线进行了自然覆冰观测试验,研究了导线直径、导线表面处理情况、覆冰类型及导线扭转对导线覆冰增长过程的影响。何青等[24]提出了考虑碰撞系数、电流焦耳热和导线表面温度等因素影响的冻结系数计算方法,并与原有方法进行对比,分析了环境参数对冻结系数的影响,通过实验验证了该方法的计算精度。楼文娟等[25]设计制作了不同覆冰厚度的新月形覆冰导线模型,模拟导线雨凇和雾凇覆冰情况,分析了导线表面粗糙度对气动力、风偏响应和舞动稳定性的影响。王强等[26]基于FLUENT和FENSAP-ICEING软件的导线覆冰增长数值模拟框架,利用三维仿真模型,研究了温度、风速、空气中的液态水含量、水滴中值直径等参数对输电线路导线覆冰质量及形状的影响,其覆冰预测模型与输电线路覆冰监测结果吻合度较高。吴建蓉等[27]基于现有拉力值反算覆冰厚度计算模型,提出拉力值质量控制方法,综合考虑线路设计冰厚、垂直档距、垂直荷载、水平应力等随覆冰厚度变化的因素,提出杆塔高差系数对模型进行优化,减小模型参数过多造成计算结果不准确,并定量研究模型参数对计算结果的影响。严波等[28]分析了覆冰厚度和风向角对输电塔动力失稳的影响,并通过静力失稳与动力失稳塔顶侧移比相等原则得到了不同覆冰厚度及风向角下输电塔动力失稳的临界平均风速。王金锁等[29]建立了档距和高差分别为800、50 m的有限元模型,分析导线在均匀覆冰、三段覆冰和线性覆冰3种覆冰形式下发生均匀脱冰和非均匀脱冰时的动力响应规律,探讨档距、覆冰厚度、脱冰率等因素对导线最大冰跳高度的影响。
胡琴等[30]采用多相流场计算的拉格朗日法,通过跟踪雨滴的运动轨迹,得到分裂子导线的碰撞系数与速度、雨滴直径、导线直径和子导线间距的关系。结果表明: 风速或雨滴直径越大,上、下风侧子导线的碰撞系数越大,在一定直径范围内,导线直径与上、下风侧子导线的碰撞系数呈负相关。闵光云等[31]采用等效替代法得到了覆冰四分裂导线中心轴处的等效气动力系数,再结合Den-Hartog横向驰振机理分析了覆冰四分裂导线等效气动力系数的稳定区,基于Hamilton原理,推导了二自由度覆冰导线的舞动方程,并求得了气动力系数的三次拟合曲线一般表达式。
然而,目前阶段的研究大多以不考虑电场情况下的覆冰导线[32]和绝缘子串的放电特性[33-37]作为研究对象,很少涉及电场因素对输电线路的影响,特别是碰撞系数数值分析方面不是很完善,有必要对此进行探讨。为此,从流体力学角度出发,建立磁流体动力方程,并以直流带电导线为研究对象,提出碰撞系数及雨滴质量流量的计算方法,利用FLUENT中的电磁场模块(magnetohydrodynamics)对导线施加电场,探究雨滴电荷密度、电场强度等参量与碰撞系数的关系,并与不考虑电场导线进行对比分析。在考虑电场的情况下,构建真实绞线模型,并与简化圆截面导线进行对比,为计算实际情况下雨滴撞击输电导线的碰撞系数提供参考。
1 导线型号选取
通常情况下,输电线路的导线为钢芯铝绞线,钢芯铝绞线是指单层或多层铝股线绞合在镀锌钢芯线外的加强型导线,如图1所示。在高压输电线路中,导线型号众多,为验证模型的正确性,需使用LGJ-400/50型号导线[38]。为进一步分析导线直径变化对碰撞系数的影响,另选取LGJ-185/45、LGJ-240/30、LGJ-300/40、LGJ-450/50 4种型号的导线使对比数据更加明显,各型号导线的具体参数如表1所示。

图1 钢芯铝绞线截面图Fig.1 Steel core aluminum stranded conductor section

表1 导线型号及参数Table 1 Conductor type and parameters
2 物理模型建立
在前处理阶段需要对流场域进行确定和划分网格,由于三维模型雨滴的运动轨迹在导线的轴向方向具有对称性,可将其视为二维流体流动模型,因此选择建立二维模型。计算区域的外边界为长方形,为减少外边界对流动的影响,流场的入口边界应设置为导线直径d的10倍以上,以确保由足够多的雨滴进入流场中。使用ANSYS ICEM对流场进行网格划分,在网格划分时既要保证网格在竖直方向的数量,同时还要保证入口网格大小一致,这样才能保证计算结果的精确性,所以需要在入口处对网格进行均匀化处理,图2所示为LGJ-450/50导线的网格划分模型。

图2 导线模型网格划分Fig.2 Mesh division of conductor model
3 数学模型建立
3.1 碰撞系数的定义
假设离导线足够远处,雨滴以速度V0水平射入流场,由于雨滴在靠近导线表面处会发生绕流现象,如图3所示。这种现象会导致部分雨滴恰好从导线表面流过,若导线截面上下两侧雨滴轨迹恰好与导线截面相切,则令这两个雨滴进入流场时的垂直距离为Y0,则可定义碰撞系数[37]为
(1)
在有限元分析中,雨滴碰撞系数也可以表示为导线捕获的雨滴数与导线截面竖直方向所占网格数之比。

图3 碰撞系数物理模型Fig.3 Physical model of collision coefficient
3.2 磁流体动力学方程
流体流场与磁场之间的耦合可以通过两个基本效应来理解:导线在磁场中运动所产生的电流,以及电流与磁场相互作用产生的洛伦兹力。通常,感应电流与洛伦兹力都倾向于与产生它们的机制相反,如导致电磁感应的运动被其所产生的洛伦兹力阻碍。
电磁场可以通过Maxwell方程进行描述,即
(2)
式(2)中:B为磁场强度,T;E为电场强度,V/m;H、D分别为磁场和电场的感应场;q为电荷密度, C/m3;j为电流密度向量。
磁场和电场的感应场和电场感应场之间存在关系
(3)
式(3)中:μ为磁导率;ε为介电常数。对于具有充分导电性能的介质(如液态金属),电荷密度q及位移电流∂D/∂t通常被忽略。
在研究流场与电磁场的相互作用时,感应电流密度的确定j至关重要。通常可用两种方法来求解电流密度:一是通过求解磁感应方程,另一种是通过求解电势方程,之后利用欧姆定律计算电流密度,本研究采用第二种方法。
电场E可表示为
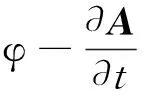
(4)
式(4)中:φ及A分别为标量势和矢量势。对于静电场,有b≪B0(其中B0表示外加磁场,b表示流体运动产生的感应磁场),磁场欧姆定律可表示为
j=σ[-∇φ+(U×B0)]
(5)
式(5)中:σ表示流体介质的电导率;U表示流体速度场。对于具有充分导电性的介质,根据电荷守恒原理
∇·j=0
(6)
电势方程可表示为
∇2φ=∇·(U×B0)
(7)
电势φ的边界条件可为
(8)
对于导电边界,φ0为边界位置指定的电势值;对于绝缘边界,n为边界的法向向量,且有φ=φ0。
利用电磁感应的知识,通过在流体动量方程和能量方程中引入附加的源项来实现磁流体动力学(magnetohydrodynamics,MHD)耦合。
对于流体动量方程,附加的源项是洛伦兹力(N/m3),表示单位体积所受的力,表达式为
F=j×B
(9)
对于流体能量方程,附加源项为焦耳热(W/m3),表达式为
(10)
对于电磁场中的带电粒子,作用于其上的洛伦兹力为
Fp=q(E+vp×B)
(11)
式(11)中:q为颗粒电荷密度,C/m3;vp为颗粒速度,m/s;Fp为作用在颗粒上的力,N/m3。
对于多相流动,假设两相界面处的电流可以忽略,则混合物的电导率为
(12)
式(12)中:σi及βi分别为第i相的电导率与体积分数。σm用于感应方程求解。
本研究应用磁流体动力学(MHD)的电势法,通过对导线施加电势形成电场,对雨滴撞击导线过程进行模拟,进而求解导线电场强度、风速、雨滴电荷密度等参量对碰撞系数的影响。
3.3 雨滴质量流量的确定
质量流量是指单位时间里流体通过有效截面的流体质量,在Fluent中需要对这一参数进行设定。由于雨滴的质量流量对碰撞系数的计算有很大影响,而目前尚没有明确的研究和统一标准。在此,基于量纲法给出了质量流量计算式。假设雨滴为均匀的球体,则雨滴的质量流量即为雨滴总质量与雨滴完全进入流场时间之比。那么,质量流量计算式可表达为
(13)
式(13)中:d为雨滴直径;N为场域中入口的雨滴数,该值与划分的网格数相等;v为雨滴速度;ρ为水的密度,ρ=1 000 kg/m3。通过式(13)求出不同雨滴直径和风速下的质量流量,如表2所示。

表2 不同外界条件下的雨滴质量流量Table 2 Raindrop mass flow rate under different external conditions
3.4 计算模型及验证
为了验证模型的正确性,将对导线表面的碰撞系数进行数值模拟计算,并与以往文献[37]中的试验结果进行对比。在ICEM中对求解域划分网格,空气及雨滴控制方程采用分离-隐式解法,对流项离散采用二阶迎风格式,离散方程组采用简单求解方法(SIMPLE)。 该模型为气液二相流模型,空气为连续相,雨滴为离散相,且雨滴所占的体积分数远小于空气,对于离散相的求解主要有两种求法,分别为欧拉-拉格朗日法和欧拉-欧拉法,欧拉-拉格朗日法以离散相颗粒为研究对象,适用于二维计算,可直观地观察雨滴的运动轨迹;而欧拉-欧拉法则是以流场为分析对象,使用与三维复杂分析,且无法得到雨滴的运动轨迹。为对比两种方法的优劣性,碰撞系数的求解以雨滴轨迹作为主要研究对象,采用欧拉-拉格朗日法进行求解。
对于材料的选取,空气的相关参数均采用默认值,离散相材料为液态水,雨滴在流场中受到重力和空气浮升力的作用,求解器选择基于稳态的压力求解器,雨滴从入口水平进入流场,出入口及边界均采用无滑移边界。在建立数学模型时,做了如下假设:
(1)雨滴速度与风速相同。
(2)雨滴直径为均匀的球形,球形直径与雨滴直径相同。
(3)雨滴形状不会因风而发生改变。
(4)雨滴只受到重力、黏性力,以及空气浮升力的作用。
与张暕等[37]所做试验进行对比,模拟环境为:导线型号LGJ-400/50,风速10 m/s,雨滴直径10、20、30、40、50 μm。图4所示为上述工况下的对比结果。由图4可见,当雨滴随空气流向导线时,雨滴直径越大,碰撞系数越高,同时碰撞系数模拟值越来越接近文献值,二者的平均误差约为1.5%,在误差允许范围之内,验证了模型的合理性。

图4 同工况下模拟与试验的碰撞系数对比[37]Fig.4 Comparison of simulated and experimental droplet impact coefficients under the same working condition[37]
4 考虑电场因素的碰撞系数分析
4.1 电场强度对碰撞系数的影响
在高压输电线路实际传输的过程中导线周围会产生电场,由于电压通常在几百千伏,所以可能会对雨滴轨迹和碰撞系数造成影响。因此有必要研究电场强度对碰撞系数的影响。由于中外尚无成熟的求解方法可借鉴,本研究采用以下方法在流场中施加电场。
Fluent中的电势模型只是应用欧姆定律求解电流密度与电势,无法求解更加复杂的电磁场与流体之间的相互作用。而要考虑这种电磁与流体之间的耦合作用,则需要使用磁流体动力学(MHD)方法。对导线设置电势,而流场边界的电势设置为零,从而形成电势差产生电压,如图5所示。在匀强电场中,设d为电场中两点间距离,则电场强度E和电压U的关系为
E=U/d
(14)
本研究中,导线入口处与导线之间的距离d=150 mm,则导线电压对应的电场强度如表3所示。
分别在导线上施加220、330、500、750、1 000 kV相电压,计算5种工况下碰撞系数的变化,结果如图6所示。
由图6可知,导线的电场强度在0~66.7 kV/cm范围内,5种导线在相同工作条件下的碰撞系数大致相同,均呈线性衰减,衰减率约为33%。另一方面,在电场密度为33.3 kV/cm的条件下,直径为

图5 对导线截面施加电势Fig.5 Electric potential is applied to the cross section of the conductor

表3 导线电压对应的电场强度Table 3 Electric intensity corresponding to conductor voltage

图6 导线电场强度与碰撞系数的关系Fig.6 The relationship between the electric field strength of the conductor and the collision coefficient
21.6 mm导线的碰撞系数降低幅度相对较小,而直径为27.63 mm导线的降低幅度较大。
根据电场的特点分析了其产生原因:电场对雨滴的作用力与雨滴的电荷量有关。场致电荷理论[38]表明,空气中存在大量移动的正离子和负离子。在电场的作用下,这些带电离子剧烈移动并与移动的雨滴碰撞。碰撞离子不断地将电荷转移到雨滴上,从而形成具有与导线带有相同电荷的雨滴。带电的雨滴将形成与外部电场相反的排斥电场,电场对雨滴的排斥作用随着雨滴电荷的增加而逐渐增大。
4.2 雨滴电荷密度对碰撞系数的影响
电荷密度是电荷在某一区域的分布密度。体积密度、面积密度和线密度之间存在差异,在本研究中,选择体积密度为例。由于在0.005~0.05 C/m3的范围内,雨滴的电荷密度对碰撞系数的影响最为明显,因此选择0~0.05 C/m3作为每个雨滴的电荷密度。
从图7中的信息可以看出,雨滴的电荷密度与碰撞系数有关。当电荷密度增加时,雨滴在电场的作用下会电离更多的电荷,使导线和雨滴具有相同的电荷极性,从而排斥雨滴并阻止雨滴与导线碰撞,从而降低碰撞系数。随着雨滴电荷密度的增加,碰撞系数呈线性下降,平均下降幅度约10%。当雨滴的电荷密度大于0.05 C/m3时,由于雨滴受到导线电场的排斥力过大,几乎没有雨滴与导线发生碰撞。
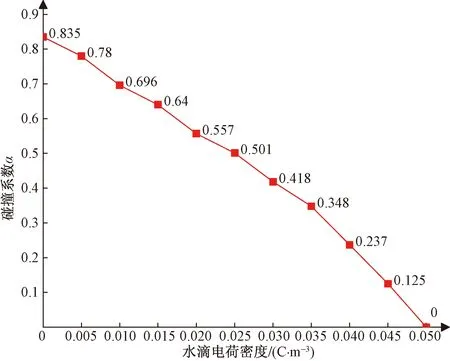
图7 雨滴电荷密度与碰撞系数的关系Fig.7 Relationship between raindrop charge density and collision coefficient
4.3 导线表面形状对碰撞系数的影响
导线表面的形状是影响碰撞系数的主要因素之一,在以往的大量文献中均把导线截面形状假想成圆形,但实际情况中导线截面应是多股导线所构成的多段圆弧形,如图8所示。

图8 导线截面模型Fig.8 Conductor section model
选取导线直径为33.75 mm,风速为4~8 m/s,对带电导线施加50 kV/cm的电场强度。通过计算,得到了真实绞线与简化圆截面导线在电场作用下的碰撞系数。表4表明在考虑电场条件下,真实绞线的碰撞系数平均比简化圆形截面的碰撞系数大16%。这是因为实际导线横截面形状不规则,使得周围电场分布不均匀。在不考虑电场的情况下,真实绞线的碰撞系数平均比简化圆截面的碰撞系数小1%。
通过后处理功能得到单根雨滴轨迹图,如图9所示,可以更加直观地看出,在导线附近经过的雨滴有一个轻微的波动,轨迹发生了改变,这种现象在真实截面下更加明显,这是因为实际绞合导线是由多段圆弧拼接组成,中间存在着很多狭小的夹缝,由于这些夹缝的存在,使得与导线碰撞的雨滴颗粒在实际模型中发生了绕流现象。
4.4 不同风速对碰撞系数的影响
选择50 kV/cm作为导线的电场强度,研究在不同风速工况下,导线表面的碰撞系数与导线之间的关系。选取雨滴直径为100 μm、电荷密度为0.01 C/m3,计算5种不同直径的导线在各工况下的碰撞系数,如表4所示。可以看出,在考虑电场工况下,风速为6 m/s时,直径为33.75 mm的导线的碰撞系数比18.9 mm导线的碰撞系数低23%。此外,以27.63 mm导线为例,当风速为4 m/s时,考虑电场的导线碰撞系数约为不考虑电场导线碰撞系数的45%。随着风速的增加,两者之间的差异逐渐减小。当风速大于10 m/s时,带电导线与不带电导线的碰撞系数基本一致。这表明在风速较大时,风速对碰撞系数的影响远大于电场力对碰撞系数的影响。

图9 单雨滴轨迹图Fig.9 Single raindrop trajectories
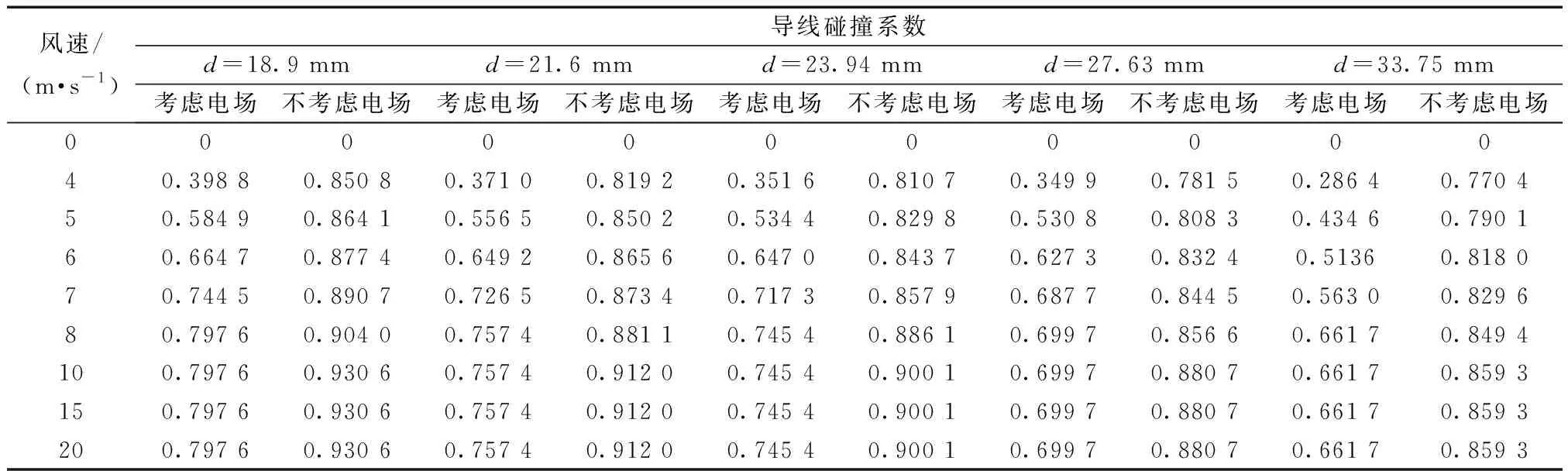
表4 不同直径d的带电与不带电导线碰撞系数对比Table 4 Comparison of collision coefficients between charged and uncharged conductors with different diameters
另一方面,在不同风速下带电导线碰撞系数均小于不带电导线。通过雨滴轨迹图可以更直观地观察到雨滴的运动轨迹。图10为雨滴轨迹云图(d=27.63 mm,v=8 m/s,E=50 kV/cm),可以看出,当雨滴接近导线时,雨滴由于受到电场的排斥作用,在流经导线时其轨迹沿导线两侧发散。
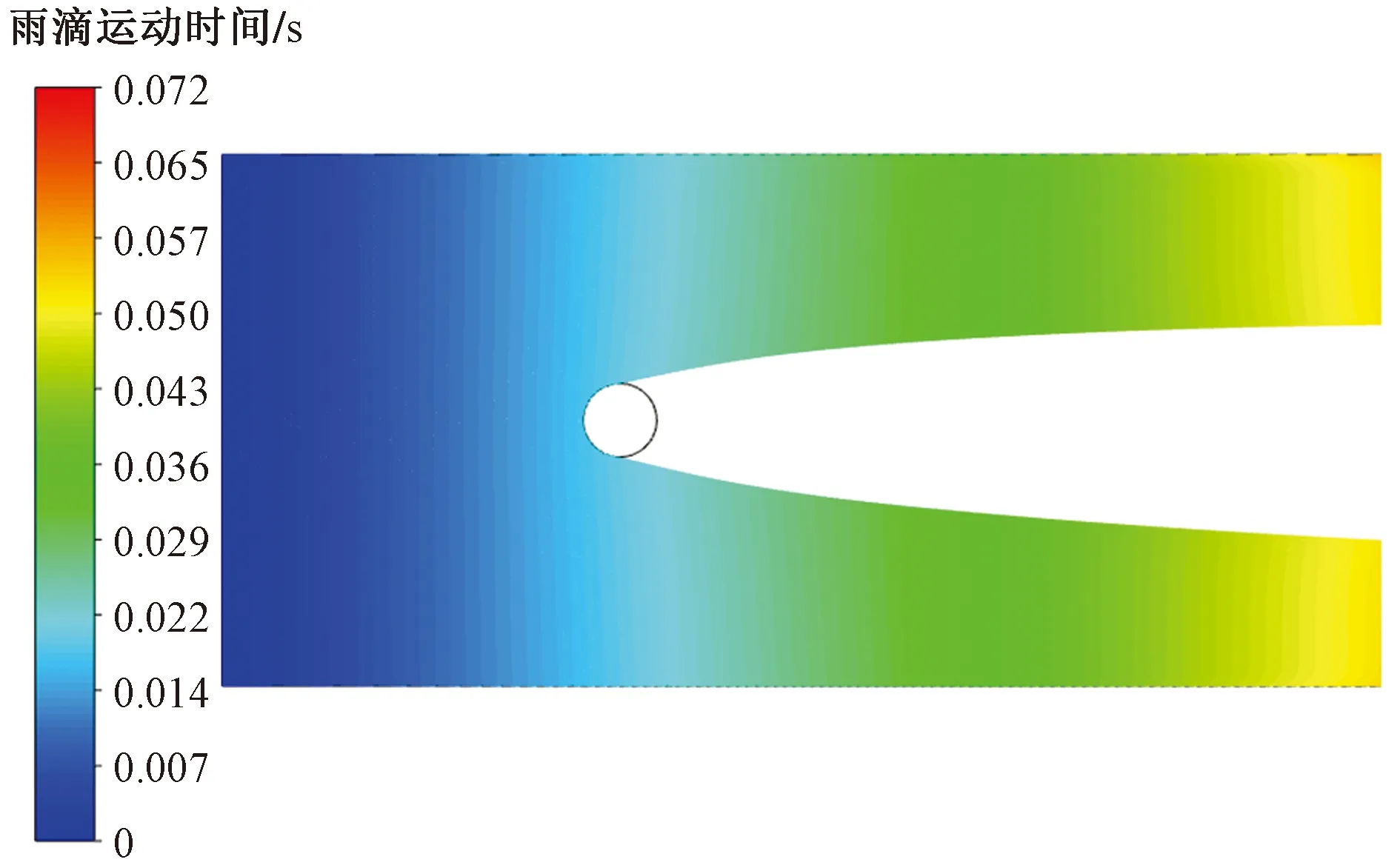
图10 考虑电场条件下导线雨滴轨迹图Fig.10 Trajectory diagram of conductor raindrops in the case of electric field
5 结论
基于流体力学理论,并利用Fluent软件计算了电场强度、风速、导线表面形状和雨滴电荷密度等参数对碰撞系数的影响,得出如下结论。
(1)碰撞系数随电场强度的增加而减小。当导线的电场强度增加到66.7 kV/cm时,导线的碰撞系数从0.835降低到0.557,降低约33%(导线直径为23.96 mm)。
(2)由于导线带电,使得导线表面产生电场,雨滴在流经导线时被电场极化并与导线极性相同。 由于导线和雨滴之间的排斥作用,部分雨滴远离导线表面,导致碰撞系数降低。
(3)输电导线实际上由多个弧段拼接而成,中间有许多小夹缝,绕流现象更加明显。因此,在不考虑导线电场的情况下,真实绞线的碰撞系数略小于简化圆形截面的碰撞系数。在直流电场作用下,实际导线碰撞系数的最大下降幅度约为无电场时导线碰撞系数的37%。
(4)在直流电场作用下,当风速达到8 m/s时,导线的碰撞系数随风速的增大而减小。超过该阈值后,碰撞系数几乎保持不变。在风速为2 m/s时,带电导线与不带电导线相比,碰撞系数降低约45%。
