大孔径开合式磁通门电流传感器探头参数设计
2022-02-06唐炜豪王向军
唐炜豪,柳 懿,王向军
(海军工程大学电气工程学院,湖北武汉 430033)
0 引言
海洋工程结构中常使用大量电化学性能不同的异种金属材料[1],如船舶上黄铜螺旋桨与碳钢船壳[2]、系统中不同管路间的组合[3]等。异种金属材料间所存在的电位差将会引发电偶腐蚀,而在腐蚀性极强的海水介质条件下电偶腐蚀效应将会得以加强引起加速腐蚀现象[4]。
目前腐蚀检测采用的方法主要有电位测量法[5]与绝缘电阻测量法[6]。这2种方法都属于间接测量法,并不能得到反映电偶腐蚀最重要的指标——腐蚀电流。之所以目前还无法测量腐蚀电流,是因为电偶腐蚀产生的电流范围广,测量精度要求高,且被测量柱体直径大,同时安装传感器过程中不能破坏柱体结构。因此,腐蚀电流检测方法需要具有非常高的灵敏度,较强的抗干扰能力,且孔径尺寸大,开合式方便拆卸等特点。
磁通门传感器因其测量精度较高[7],成本较低,结构简单[8],且技术较为成熟[9],成为了腐蚀电流测量的首选。本文提出了一种基于磁通门原理[10]的大孔径开合式腐蚀电流检测探头,并通过有限元仿真验证了不同探头参数下磁通门脉冲特性。
1 磁通门探头的原理与模型
磁通门电流传感器探头主要由激励源、磁通门探头、后处理电路和被测柱体组成,其原理如图1所示。
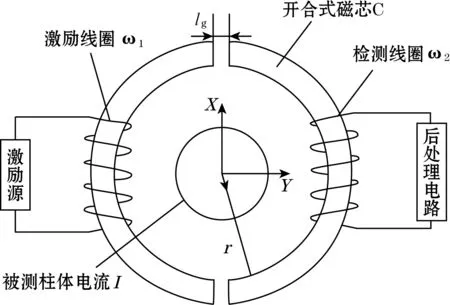
图1 开合式磁通门电流传感器探头原理图
其中磁通门探头部分由一个双边开合式环形磁芯C和绕制在磁芯上的激励线圈ω1和检测线圈ω2组成,磁通门探头正常工作时,激励源向激励线圈ω1通入交变电流,使得磁芯C在正负饱和状态之间不断变化,此时检测线圈ω2上会产生正负变化的感应电流,当被测柱体电流I不为0时,感应电流的正负变化不对称,后处理电路通过解调感应电流中的不对称偏置,检测出被测柱体电流I。
由于开合式的安装方法,使得磁芯C被分为2个部分,2部分磁芯接触位置存在微小气隙,图1中为了直观展现,气隙设置较为明显,将单个气隙宽度记为lg,为了便于分析,将两段气隙的宽度视为一致,以磁芯C的中心点为原点构建X-Y坐标系,记磁芯内径和外径的平均值为r。
针对待测电流,根据气隙磁芯的全电流定律有:
I=2Hgxlg+2Hxlc
(1)
式中:Hgx为待测电流在磁芯气隙处产生的磁场;lc为半边磁芯的平均磁路长度;Hx为待测电流I在磁芯上产生的恒稳磁场。
环形磁芯中lc≈πr,则式(1)表示为:
(2)
当气隙宽度lg恒定时,待测电流在磁芯上产生的磁场与磁芯半径成反比。当磁芯孔径恒定时,气隙宽度lg越大,待测电流在磁芯上产生的磁场越小。
记激励线圈在磁芯上产生的磁场为H1(t),同理可根据全电流定律得出:
(3)
式中:N1为激励线圈匝数;I1(t)为激励线圈中通入的交变电流;Hg1为激励电流在磁芯气隙处产生的磁场。
当I1(t)为正弦激励时有:
I1(t)=Asin(2πft)
(4)
式中:A为激励电流的幅值;f为激励电流的频率;t为时间变量。
设磁芯上的平均磁场为Hc,则待测电流和激励线圈共同作用时:
(5)
式中Hgx和Hgl分别与待测电流I和正弦激励幅值A成正比。
实际研究中需要结合气隙边缘磁阻[11]对其进行分析。
为了简化模型,不考虑磁芯磁滞,图2为磁芯材料的理想B-H曲线,其中Hm和Bm分别为磁芯的饱和磁场强度和饱和磁感应强度,则可将磁通门正常工作时磁芯相对磁导率简化为下式:
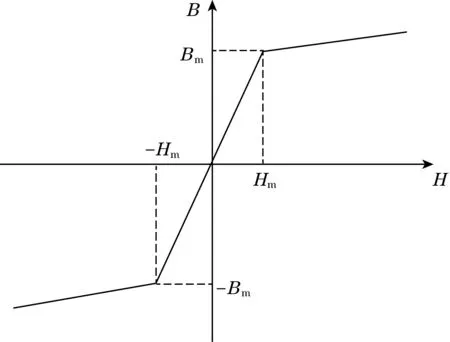
图2 磁芯的B-H曲线
(6)
式中μr1和μr2分别为磁芯工作在不饱和状态和饱和状态的相对磁导率,μr1>>μr2。
当磁通门传感器正常工作时,开合式结构不可避免地存在磁芯气隙,根据磁路的欧姆定律,可列出其磁路方程[12]:
(7)
式中:S为沿磁路长度的磁芯横截面积;N2为检测线圈匝数;Φ(t)为磁芯横截面的磁通量;μ0为真空中的磁导率,μ0=4π×10-7H/m,此处将其等同于空气磁导率;I2(t)为检测线圈上的感应电流。
由于大孔径探头磁芯磁路较长,即πr>>lg,且磁通门探头选取的磁芯材料为高磁导率材料,所以磁芯材料未磁饱和时有μr1>>1,此时式(7)中气隙磁阻和磁芯材料磁阻都不能忽略。
记R和L分别为检测线圈中的电阻分量和电感分量,由法拉第电磁感应定律和欧姆定律可知:
(8)
联立式(7)和式(8)有:
(9)
将式(9)利用相量法表示为
(10)
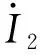
化简得:
(11)
根据式(11)可知,激励线圈产生交变电流时,检测线圈的输出电流与开合式磁通门的磁路参数lg、r,激励线圈和检测线圈匝数N1、N2,检测线圈负载R、L,以及激励电流角频率ω,磁芯截面积S,磁芯磁导率变化曲线μr有关。
磁通门正常工作时,其激励线圈电流I1,磁芯上的磁场Hc,感应线圈电流I2波形如图3所示,磁芯在正弦激励下于正负饱和之间不断变化,当磁芯上的磁场Hc<-Hm或Hc>Hm时,磁芯处于饱和状态,此时磁导率μr2很小,I2接近为0。当磁芯状态不饱和即μr=μr1时,检测线圈电流波形呈现出如图3所示的脉冲电流,由于待测电流的存在使得激励磁场发生偏置,进而导致如式(12)所示的检测线圈不对称电流,通过后处理电路解调不对称偏置可求得被测电流的大小。

图3 磁通门效应示意图

(12)
对式(11)取模值,令ω=2πf,可以求出t=t2时检测线圈的磁通门脉冲电流正峰值为
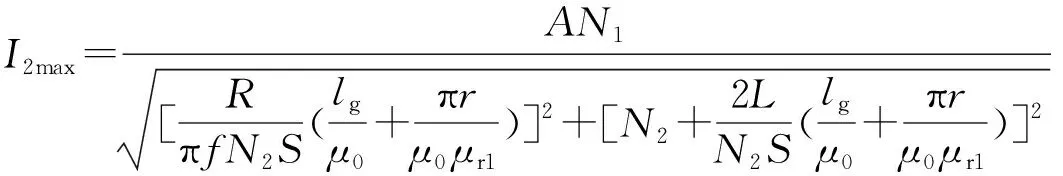
(13)
同理,检测线圈电流脉冲正峰值的相位差为
(14)
磁通门效应直接使得磁通门脉冲的正负不对称,而磁通门传感器的检测精度也很大程度上依赖磁通门脉冲的峰值大小,在实际的传感器参数设计过程中,需要考虑不同参数对脉冲的影响,令磁通门脉冲峰值达到合理程度。
2 仿真分析
为了研究不同参数对磁通门传感器输出的影响,利用COMSOL有限元仿真软件对开合式磁通门传感器的输出特性和磁场分布进行分析计算,需要说明的是,仿真过程中改变相应一种参数,其他参数保持不变。
2.1 模型建立与参数设定
有限元仿真建立如图4所示,整个磁通门探头模型分别由激励线圈,检测线圈,开合式磁芯以及待测大轴电流组成。
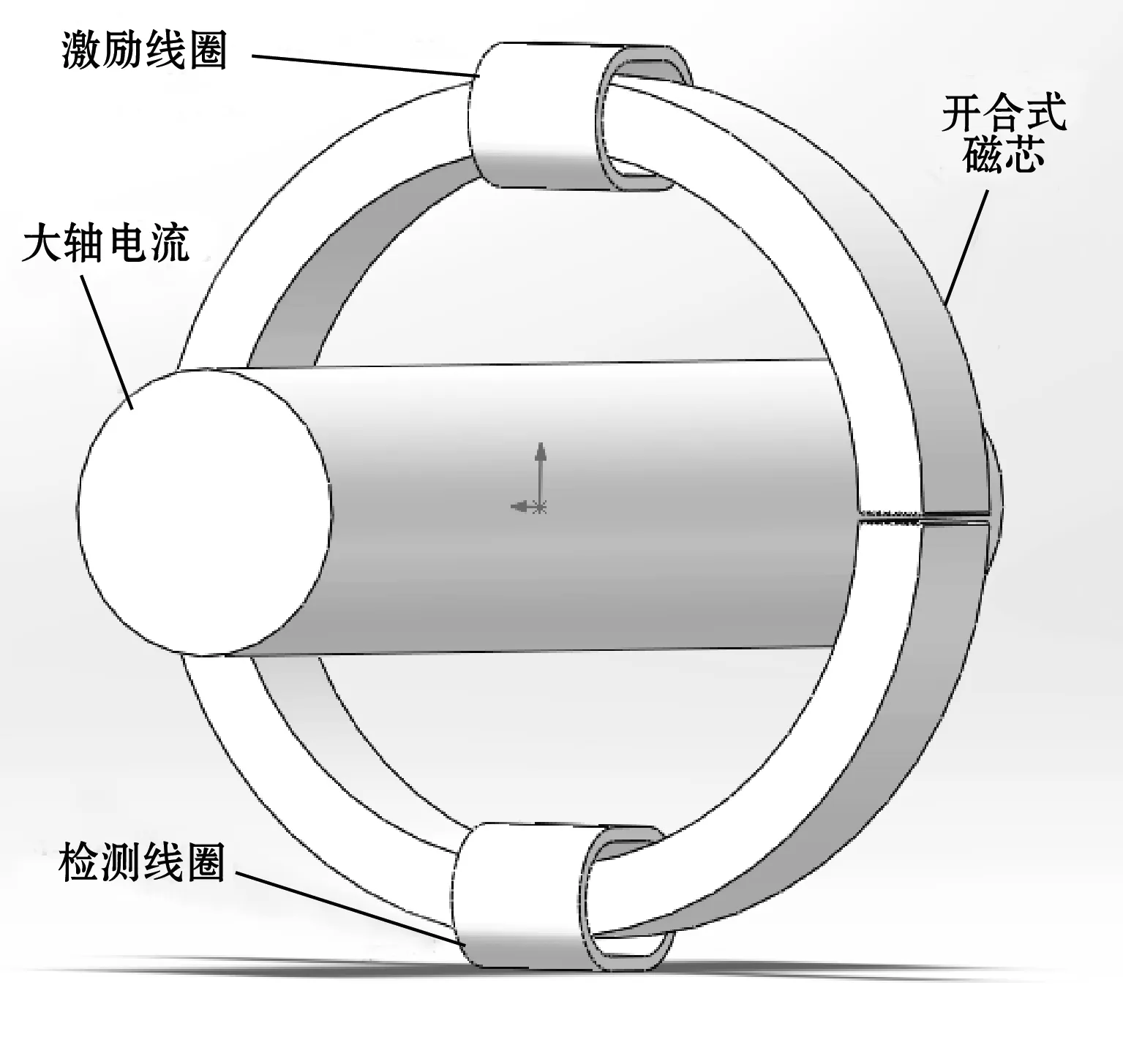
图4 磁通门结构示意图
针对实际需要对开合式磁通门传感器进行参数设计,基本参数如表1所示。
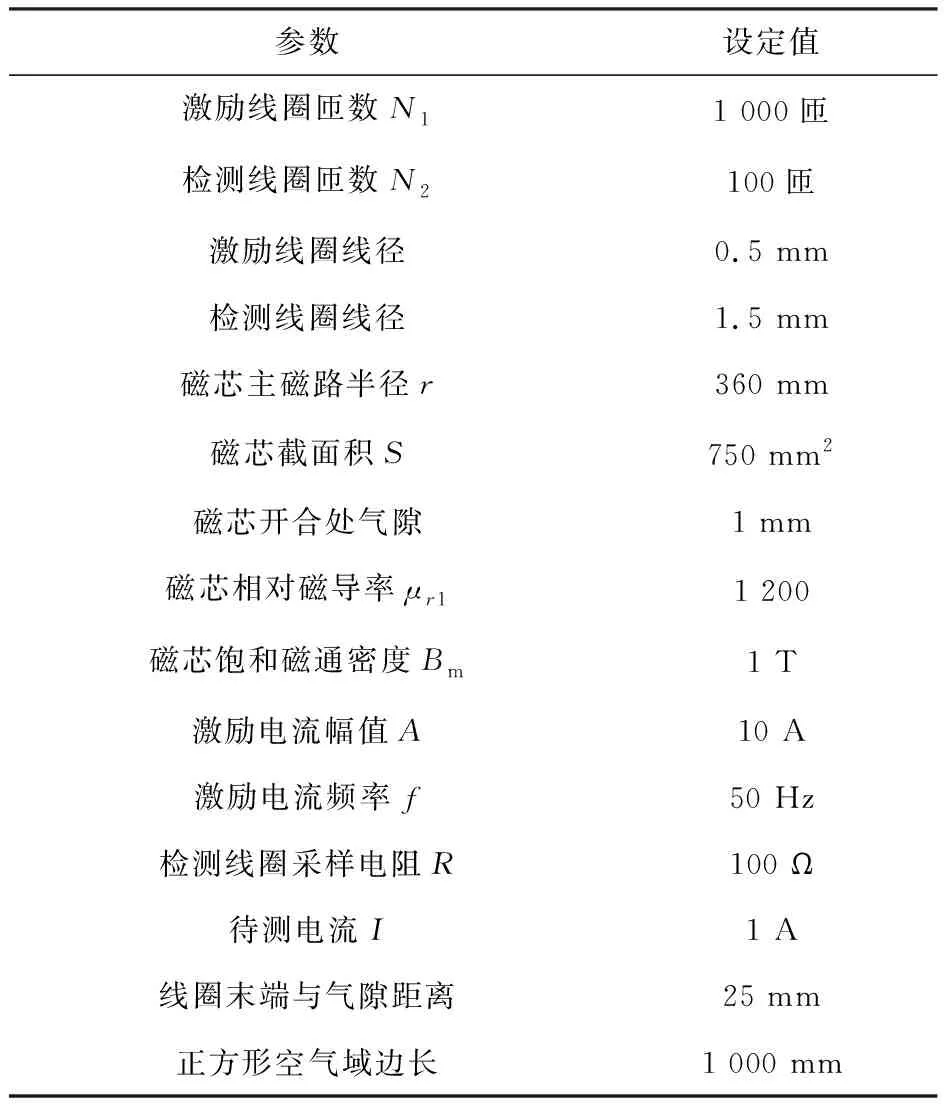
表1 仿真参数设置表
由于磁通门的软磁材料磁芯具有非线性磁化特性,为了简化模型,假设磁芯介质各向同性,同时忽略磁滞效应,建立瞬态场下的控制方程如式(15) 中Maxwell方程组的微分形式所示:
(15)
式中:D为电位移矢量;H为磁场强度矢量;E为电场强度矢量;B为磁感应强度矢量;ρ为自由电荷的体密度;γ为电导率。
仿真过程中引入矢量磁位A和标量磁位φ如式(16)所示,结合式(15)即为有限元仿真的数学模型。
(16)
2.2 线圈绕制方式分析
通过计算待测电流在磁芯上产生的磁通密度模值,可以分析出待测电流在磁芯上产生的偏置磁场,图4中建立的磁通门模型为了便于直观表示,将激励线圈与检测线圈分置于磁芯两端缠绕,实际线圈绕制的过程中,为了防止被测电流偏离磁芯中心带来的测量误差,激励线圈与检测线圈皆均匀地绕制在整个完整磁芯上。图5为待测电流位置在x和y方向偏心时,检测线圈绕制的磁芯上磁通密度模值大小。比较图中2种线圈绕制方式,可以发现随着待测电流偏心程度增加,均匀绕制线圈的磁芯检测线圈部分的磁通密度模值变化程度较小,可见均匀的缠绕线圈是大孔径磁通门准确测量电流的前提。

(a)待测电流位置在x方向变化

(b)待测电流位置在y方向变化图5 不同绕线下待测电流在磁芯上平均磁通密度模值
在均匀绕制线圈的基础上,由于开合式磁芯中气隙附近的软磁材料难以进入磁饱和状态,当不能进入磁饱和时检测线圈便不能产生磁通门偏置,所以在绕制检测线圈时线圈末端需要与气隙保持一定的距离。图6为激励电流工作在最大值时,距离气隙不同位置的磁芯截面磁通密度模值的平均值随气隙大小的变化,可以看出随着气隙的增大,磁芯上的截面磁通密度模值降低,距离气隙越近的截面降低速度越快,当气隙大小分别为1.3、1.5、1.8、2、2.2 mm时,距离气隙5、10、15、20、25 mm的磁芯材料未达到饱和磁通密度。可见,若要保持2 mm气隙内的开合式磁通门探头准确性,其检测线圈末端绕制时至少需要与气隙保持20 mm以上的距离。当然,在实际绕制的过程中,还需考虑磁芯气隙漏磁带来的线圈漏感影响,气隙漏感与周围的磁性材料以及线圈的位置尺寸等参数密切相关[13]。
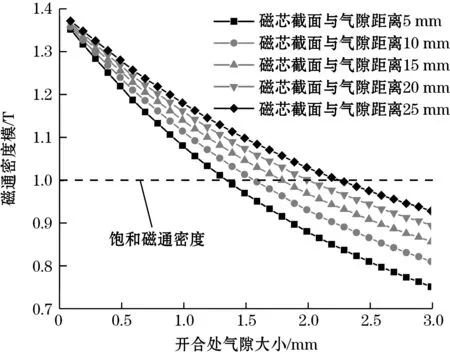
图6 气隙大小变化对不同磁芯截面上磁通密度的影响
2.3 磁通门磁芯参数分析
计算不同开合气隙大小时,待测电流在磁芯上产生的平均磁通密度模值如图7所示,可以看出,开合处气隙越大,待测电流在磁芯上产生的磁通量就越小,当磁芯开合气隙分别为0.1、0.5、1 mm时,磁芯上的磁通密度模值仅为完全闭合磁芯的90.3%,66.4%和51.0%,可见微小气隙就能使磁芯对待测电流产生的磁场感应能力下降。
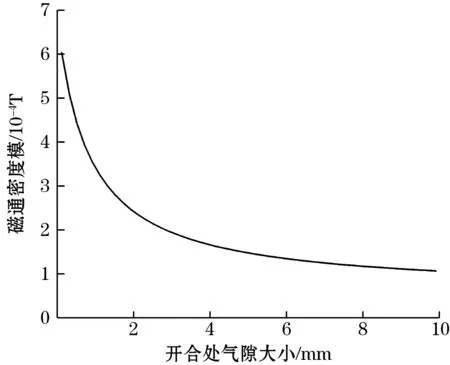
图7 气隙大小对磁芯上平均磁通密度模值的影响
由于磁通门电流传感器是根据待测电流在磁芯上产生的磁场来检测被测电流,所以为了精确测量待测电流,开合处气隙需要尽可能的小。不同开合气隙大小下检测线圈电流波形如图8所示,当开合气隙增大时,磁通门脉冲峰值明显减小,脉冲宽度增大,这将导致传感器在后处理之后精度降低,量程减小。

(a)检测线圈电流波形

(b)检测线圈电流峰值变化规律图8 气隙对磁通门脉冲的影响
随着环形磁芯的半径增大,待测电流在磁芯上产生的磁通密度模值变化规律如图9所示,由图可知,随着磁通门磁芯半径的增大,待测电流在磁芯上产生的偏置磁场减小,检测难度更大。图10为相同激励电流下不同磁芯半径的检测线圈磁通门脉冲,可见,磁通门脉冲峰值随着孔径的增大而减小。H Can等[14]制作的直径为15 mm的环形磁通门磁场传感器动态范围内误差为±0.01%,被其视作最佳几何结构,增大环形孔径必然导致传感器误差增加,使得后处理电路设计难度增大。
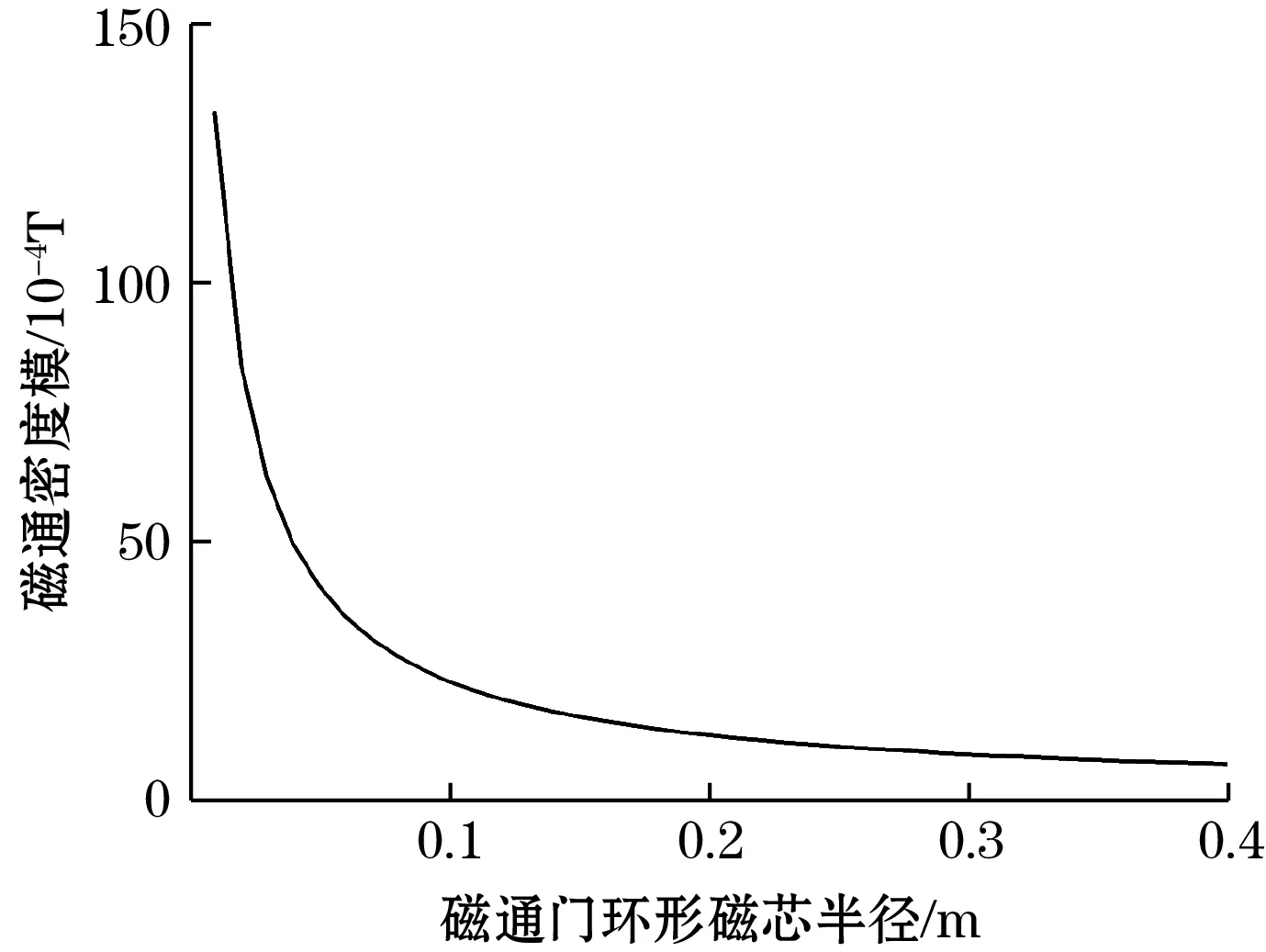
图9 磁芯半径对磁芯上平均磁通密度模值的影响
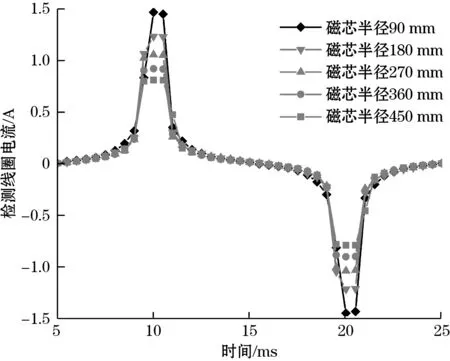
(a)检测线圈电流波形
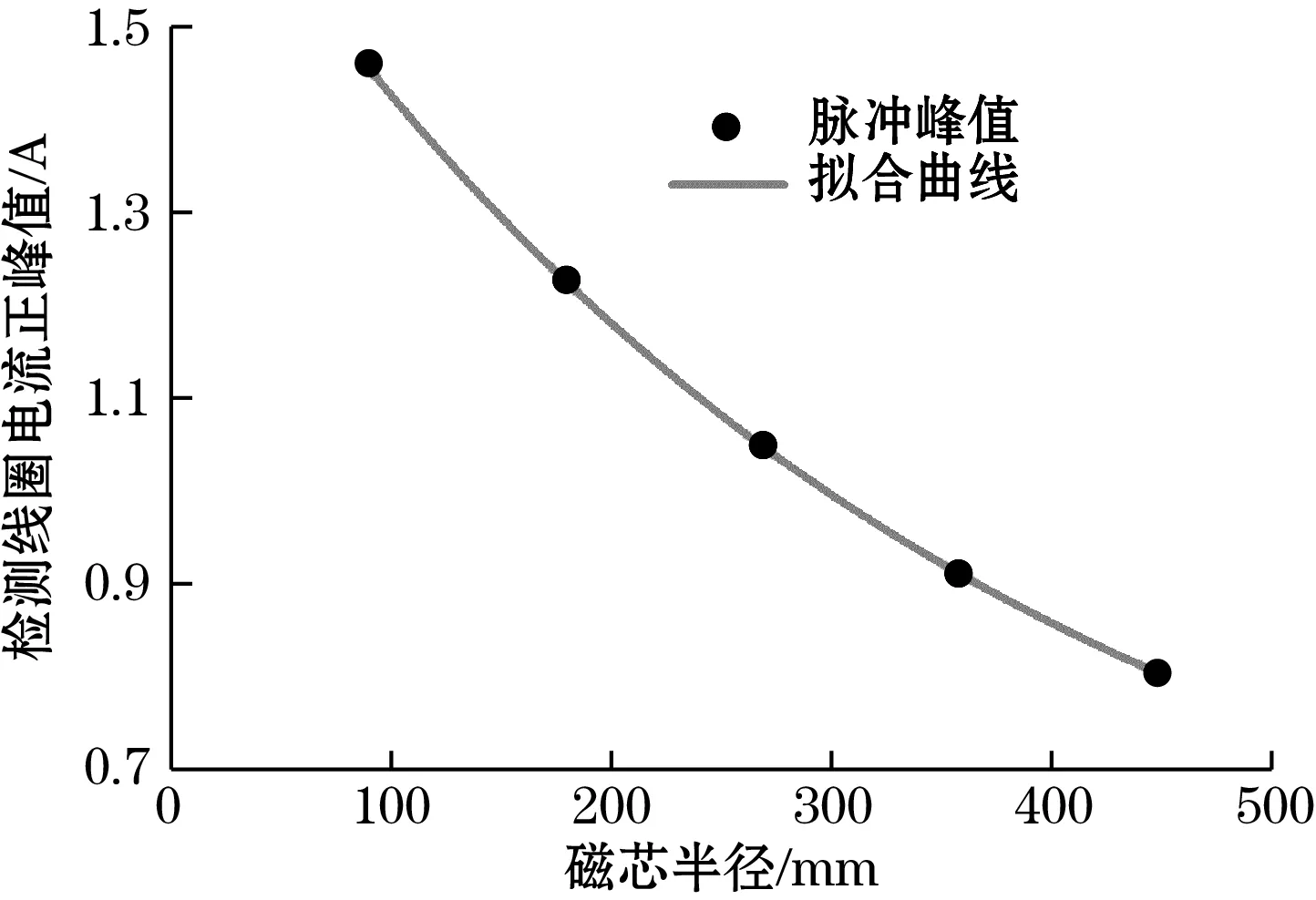
(b)检测线圈电流峰值变化规律图10 磁芯半径对磁通门脉冲的影响
随着环形磁芯截面积的增大,待测电流在磁芯上产生的磁通量平均值变化规律如图11所示,由图可知,磁芯上的磁通量与磁芯截面积成线性关系,磁芯截面积越大,待测电流在磁芯上产生的磁通量就越大。图12为不同截面积下检测线圈中磁通门脉冲波形,截面积越大,磁通门脉冲峰值便越大。然而实际传感器设计过程中需要充分考虑磁芯材料的用量,增大磁芯截面积不仅增大了磁芯成本,而且使得传感器的质量增大,不利于满足工业市场需求。

图11 磁芯截面积对磁芯上平均磁通量的影响
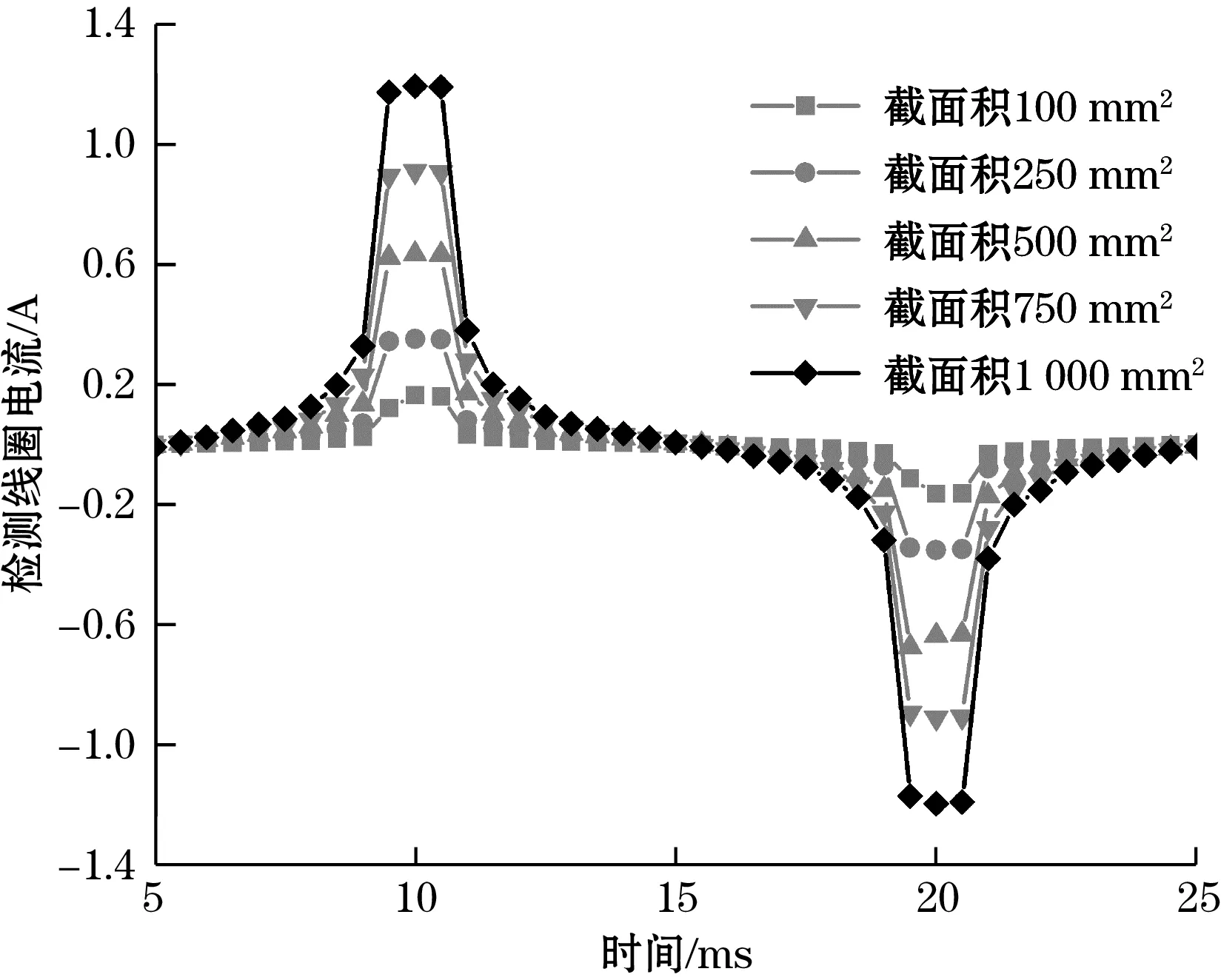
(a)检测线圈电流波形
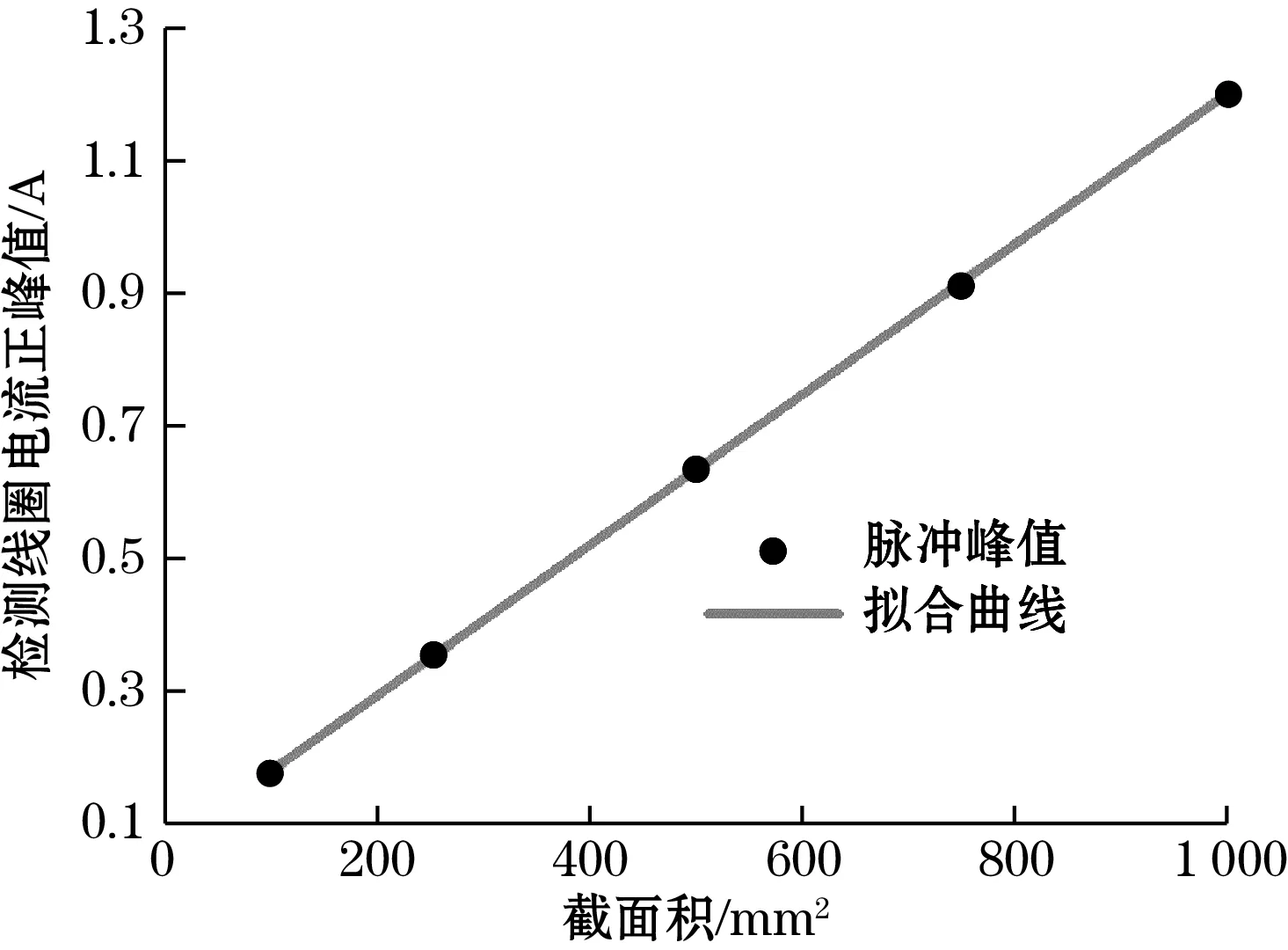
(b)检测线圈电流峰值变化规律图12 磁芯截面积对磁通门脉冲的影响
磁芯材料的初始磁导率是影响磁通门精度的重要因素,图13中,随磁芯相对磁导率增大,待测电流在磁芯上产生的平均磁通密度模值同样增大,可见高磁导率磁芯材料对待测电流产生的磁场有更强的感应能力。图14为不同磁芯磁导率下检测线圈磁通门脉冲的波形,磁导率越大,检测线圈的磁通门脉冲峰值越大,可见高磁导率材料可以使得磁通门传感器探头测量准确度更高。
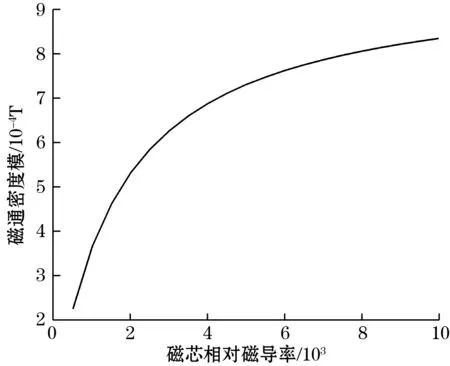
图13 磁芯相对磁导率对磁芯上平均磁通密度模值的影响

(a)检测线圈电流波形

(b)检测线圈电流峰值变化规律图14 磁芯相对磁导率对磁通门脉冲的影响
2.4 磁通门电路参数分析
图15为激励电流大小对磁通门脉冲的影响,随着激励电流幅值的增加,磁通门脉冲峰值越大,脉冲宽度越窄,这表明增大激励电流可以增加传感器的精度,但增大激励电流会增加能量损耗,在实际传感器参数选取过程中应在精度范围内合理选取激励电流大小。
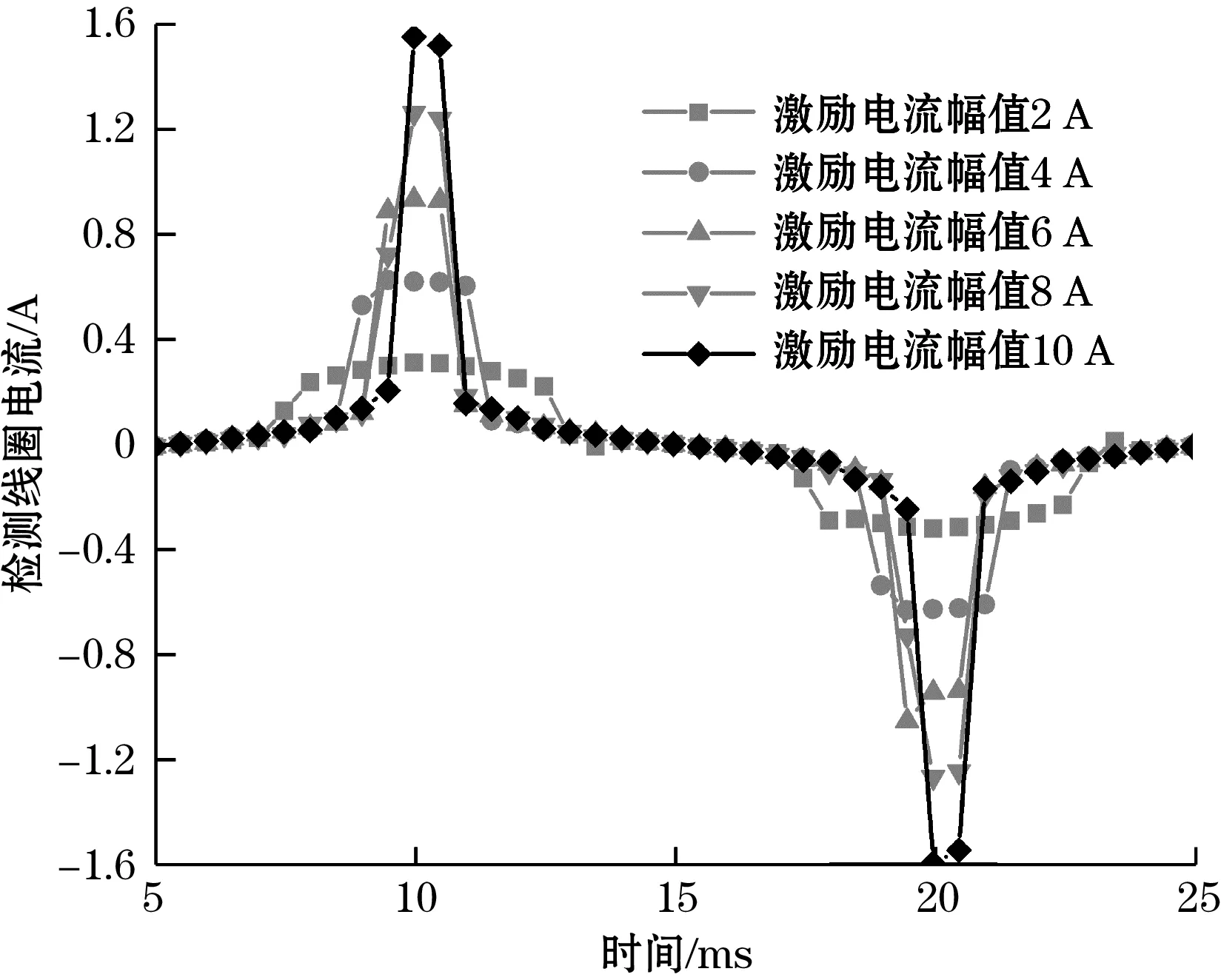
(a)检测线圈电流波形

(b)检测线圈电流峰值变化规律图15 激励电流幅值对磁通门脉冲的影响
当检测绕组匝数增加时,可以有效地增大磁通门脉冲峰值,但是匝数的增加使得检测绕组电流相位偏移,脉冲宽度增大,如图16所示,不仅不利于磁通门信号的后处理,而且增大的脉冲宽度使得磁芯在饱和状态的时长降低,传感器量程减小。图17为激励线圈匝数对磁通门脉冲的影响,激励线圈匝数的增加可以有效地增大磁通门脉冲的峰值,有利于提升磁通门后处理时的精度,但是实际设计过程中需要考虑线圈线径和成本,合理选取线圈匝数。
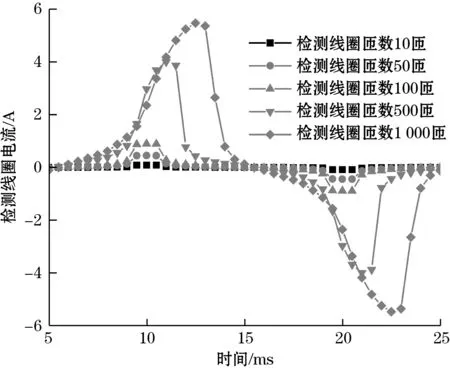
(a)检测线圈电流波形
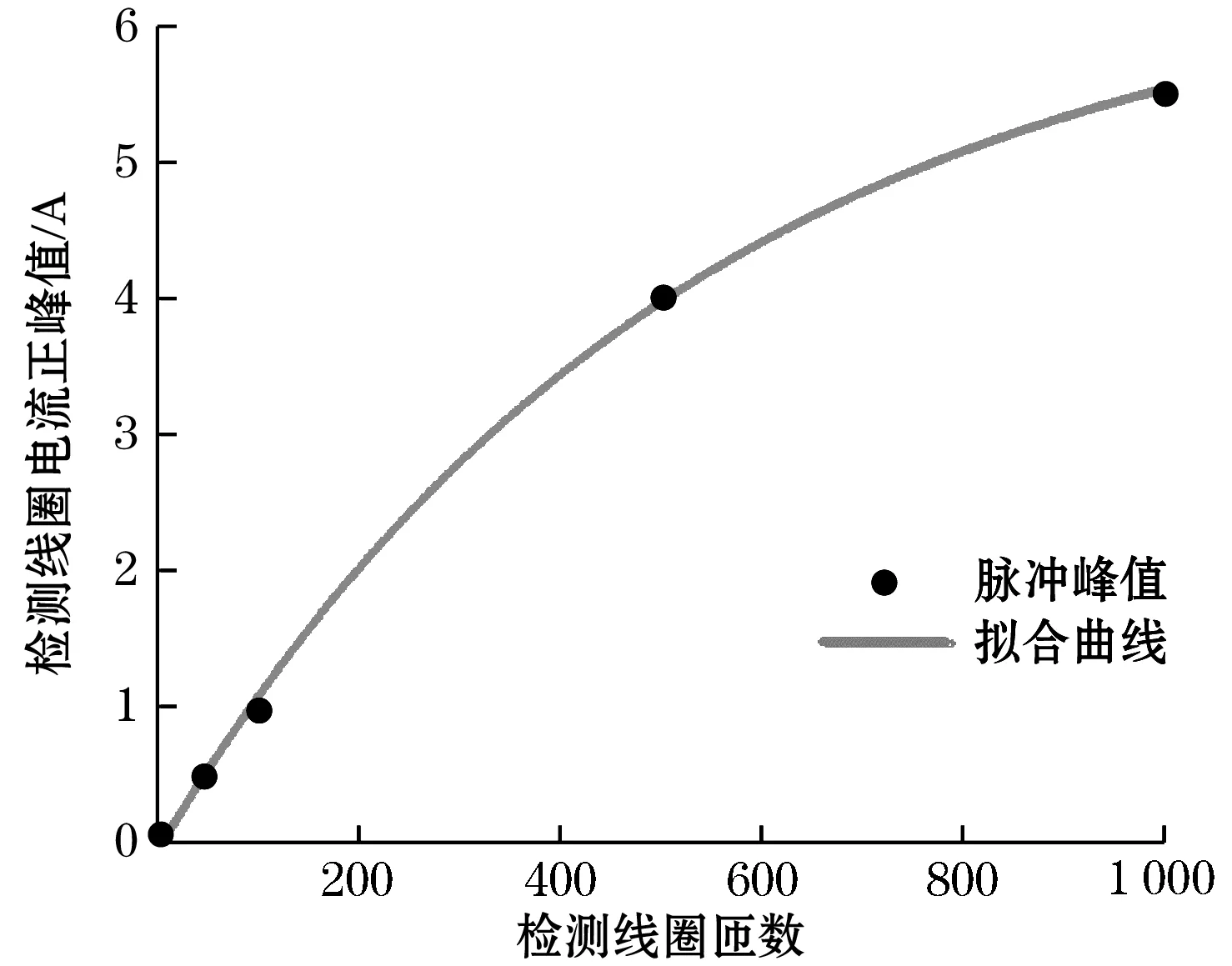
(b)检测线圈电流峰值变化规律图16 检测线圈匝数对磁通门脉冲的影响
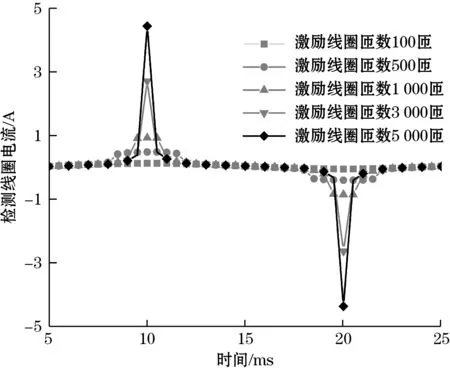
(a)检测线圈电流波形

(b)检测线圈电流峰值变化规律图17 激励线圈匝数对磁通门脉冲的影响
激励电流频率的增加使得检测线圈周期性电流信号频率增大,如图18所示,磁通门脉冲峰值同样增大,然而过大的频率会导致线圈中的电感分量增大,使得磁通门脉冲相位发生了一定程度的偏移,如图18(d)所示。
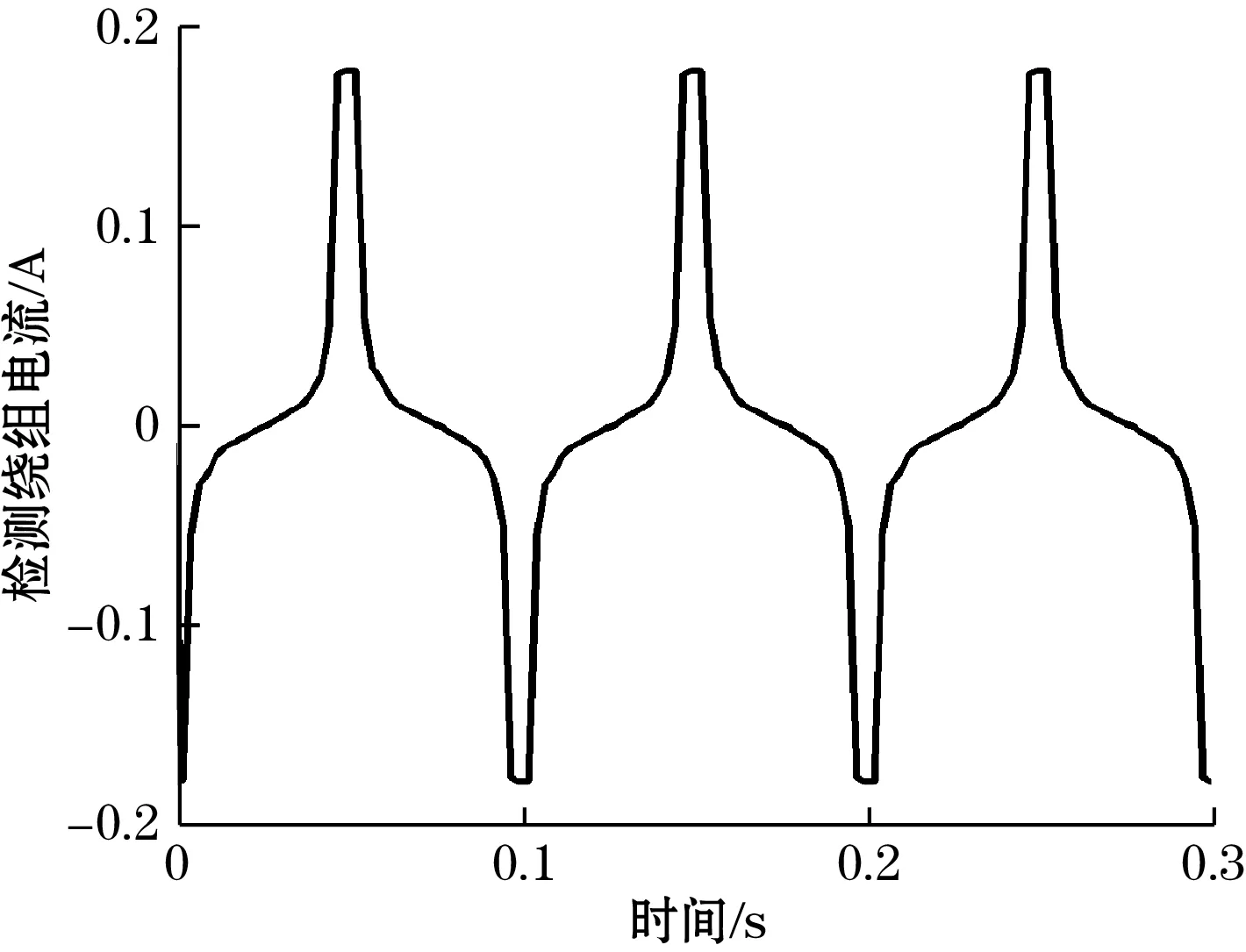
(a)激励频率为10 Hz
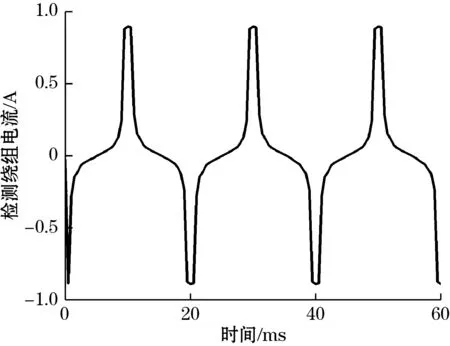
(b)激励频率为50 Hz
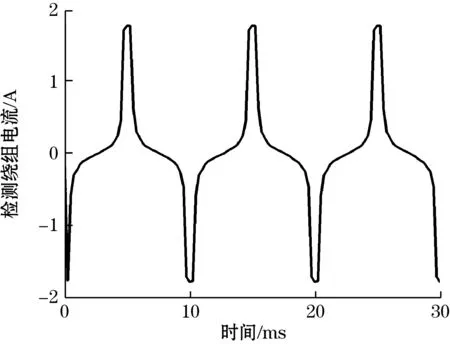
(c)激励频率为100 Hz
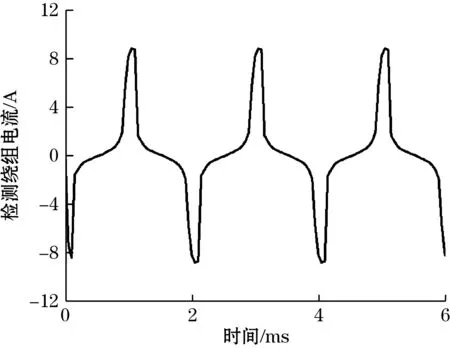
(d)激励频率为500 Hz图18 不同激励频率下对磁通门脉冲的影响
通过分析检测线圈中的电阻分量对磁通门脉冲的影响,如图19所示,可见检测线圈中的电阻分量直接影响了磁通门脉冲的峰值大小,电阻分量越小,磁通门脉冲峰值越大。电感分量对于磁通门检测线圈中电流波形的影响如图20所示,可以发现当电感分量增大时,磁通门信号相位偏移也增大,当电感分量为500 mH时无法准确识别磁通门脉冲,在实际绕制线圈过程中不可避免的产生线圈电感,利用物理模型可以较为准确地评估环形磁通门磁场传感器的检测线圈电感[15],对环形磁通门电流传感器具有一定的借鉴作用。

(a)检测线圈电流波形
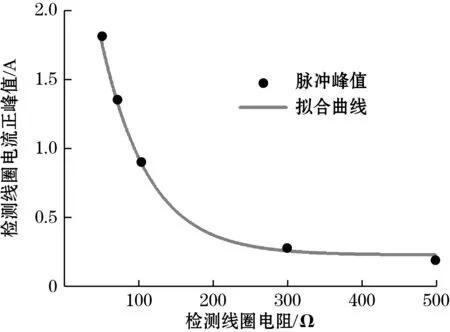
(b)检测线圈电流峰值变化规律图19 检测线圈电阻分量对磁通门脉冲的影响

(a)检测线圈电流波形
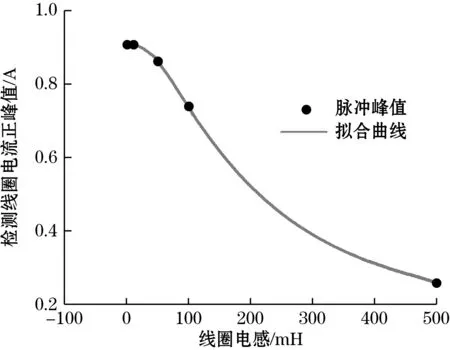
(b)检测线圈电流峰值变化规律图20 检测线圈电感分量对磁通门脉冲的影响
3 结论
本文探讨了大孔径开合式磁通门电流传感器探头的数学解析模型,通过将待测电流引起的磁场偏置影响带入磁芯磁导率,联立磁芯磁路方程和检测线圈的电路方程,结合相量法得出了开合式磁通门传感器的检测线圈电流脉冲峰值计算公式。
通过仿真讨论了实际工作中开合式磁通门探头的不同参数对磁通门脉冲的影响(包括磁芯的半径r,气隙大小lg,磁芯截面积S,磁芯相对磁导率μr1,激励线圈和检测线圈匝数N1、N2,检测线圈负载R、L,以及激励电流幅值A,频率ω),为大孔径开合式磁通门电流传感器的探头设计提供了理论依据。
